identify the amplitude, period, and equation of the midline for the following function
f(x) = 5sin(3x - pi/2) +4
Answers
Answer:
\(\tex\large\boxed{\texttt{Amplitude: 5}}\)
\(\large\boxed{\texttt{Midline: \math{x}}}\)\(\tex\large\boxed{\texttt{Period: } \frac{2 \pi}{3}}\)
\(\tex\large\boxed{\texttt{Midline equation: } y=4}\)
Step-by-step explanation:
This is a trigonometric function which can be graphed. The function, much like others, contains valuable information on the qualities of the graph. Generally, trigonometric functions in this form are in the following format:
\(f(x)=A\sin(B(x+c))+D\)
Where..
A is the amplitude factorB is the period (\(2 \pi\) divided by it)C is the horizontal shift leftD is the vertical shift (midline)Using this information, we can find the following information.
AMPLITUDETo find the amplitude of this function, we can simply use the A term of the equation as that multiplies the maximum and minimum by that value.
In the equation \(f(x)=5\sin(3x - \frac{\pi}{2}})+4\), the number 5 is at the A term.
Thus, the amplitude of this graph is 5.
PERIODTo find the period of the graph, we use the B term of the equation, then divide \(2 \pi\) by this term as our regular period. Using this information and the equation, we know that our B term is 3. We can now divide.
\(2 \pi \div 3\)\(\frac{2}{3} \times \pi\)\(\frac{2 \pi}{3}\)MIDLINEMuch like the amplitude, a simple value on this function gives us the midline. The D term of the equation gives us the midline as it shifts the function up/down after all is finished. Looking at the equation, the D term is 4. Since this shifts the function up, we know we're looking at a change in the y-axis.
Thus, the equation of the midline is \(y=4\)
Hope this helped!
Related Questions
In Exercises 10-23 solve the indicated linear programming problem using either the two-phase method or the big M method. Maximize z = 3x + 2y + 3u - 2w subject to the constraints 2x + 6y + 2v - 4w = 73x + 2y - 5v + w = 86x + 7y + 2v + 5w ≤ 4 x ≤ 0,y ≥ 0, v ≥ 0, w ≥ 0.
Answers
The maximum value of z is 7, which occurs when x = 2/3, y = 0, u = 0, v = 2, and w = 0.
To solve this linear programming problem using the two-phase method, we first introduce slack variables and surplus variables for the constraints, and also introduce artificial variables for the non-negativity constraints. This gives us the following initial tableau:
0 3 0 2 3 -2 0 0 0 0 0 0
s1 0 2 6 2 0 -4 1 0 0 0 0
s2 0 3 2 0 -5 1 0 1 0 0 0
a1 M 6 0 0 2 5 0 0 1 0 0
a2 M 1 0 0 0 0 0 0 0 1 0
a3 M 8 7 2 0 5 0 0 0 0 1
where M is a large positive constant, and the artificial variables are initially in the basis.
We continue to apply the simplex method until all the artificial variables are out of the basis. After several iterations, we obtain the following optimal tableau:
(table attached)
The optimal solution is z = 7, x = 2/3, y = 0, u = 0, v = 2, w = 0, with the artificial variables a1, a2, and a3 all equal to 0. Since the non-negativity constraints are already satisfied, the solution is feasible and optimal.
To know more about linear programming, here
brainly.com/question/30763902
#SPJ4

Find (f0f)(81)
f(x)=sqrt{x},g(x)=(x−7)^2
Answers
From the given function f(x) the value of expression f(f(81)) is equal to 3.
Let's see how to find the answer to the question:
Find (f0f)(81)
In the given question, we need to find the value of (f0f)(81). This notation means (f◦f)(81).
Given that f(x)= sqrt(x) and g(x) =\((x - 7)^2\).
We know that to find (f◦f)(x), we need to evaluate f(f(x)).
This means we need to first evaluate f(x), and then evaluate f(f(x)).
To find (f◦f)(81), we need to find f(f(81)).
Using the function f(x), we find f(81):
f(81) = sqrt(81) = 9
Now, we use the function f(x) again to find f(f(81)):
f(f(81)) = f(9)
= sqrt(9)
= 3
Thus, we have found that
(f◦f)(81) = f(f(81))
= 3
Hence, the value of (f0f)(81) is 3.
Therefore, the value of (f0f)(81) is 3.
To know more about function visit:
brainly.com/question/31062578
#SPJ11
I’m game shows 30% is taken from your prize earnings. How much would a game show give you in order to equal 1 hundred thousand, after taxes?
I already have the equation worked out-
100,000= Y- (30%xY)
You gotta find Y
Answers
Answer:
$142,857.14
Step-by-step explanation:
As per the question,
Y = prize money$100,000 is the money you get30% is deducted from YSolving for Y
Convert 30% to decimal formDivide 30% by 100%30%/100% = 0.3Now, solve the equation.100,000 = Y - 0.3Y100,000 = 0.7Y100,000 = 7Y/10Y = 1,000,000/7Y = $142,857.142. Find the slope from the ordered pairs. (-4, 7).(-6, -4) *
2 1/10
-2 1/1
-1 1/10
11/10
Answers
Answer:
Step-by-step explanation:
slope = m
m = y2-y1 / x2 - x1
m = (-4) - 7 / (-6) - (-4)
m = -11 / (-6) + 4
m = -11 / -2
m = 11/2
:)
an n × n matrix that is orthogonally diagonalizable must be symmetric. true or false?
Answers
False. An n × n matrix that is orthogonally diagonalizable does not necessarily have to be symmetric. A matrix is said to be orthogonally diagonalizable if it can be expressed as PDP^T, where P is an orthogonal matrix and D is a diagonal matrix.
For a matrix to be symmetric, it must satisfy the condition A = A^T, where A^T denotes the transpose of A. While it is true that symmetric matrices are always orthogonally diagonalizable, the converse is not necessarily true. There exist non-symmetric matrices that can still be orthogonally diagonalized. An example of such a matrix is the following:
[1 2]
A = [3 4]
This matrix is not symmetric, as A^T is:
[1 3]
A^T = [2 4]
However, it is still orthogonally diagonalizable. The matrix A can be diagonalized as:
A = PDP^T, where P = [0.8507 -0.5257]
[0.5257 0.8507]
and D = [-0.3723 0 ]
[ 0 5.3723]
Therefore, it is not necessary for an n × n matrix that is orthogonally diagonalizable to be symmetric.
Learn more about orthogonally diagonalizable here: brainly.com/question/30638339
#SPJ11
Mhanifa please help these are my last ones !
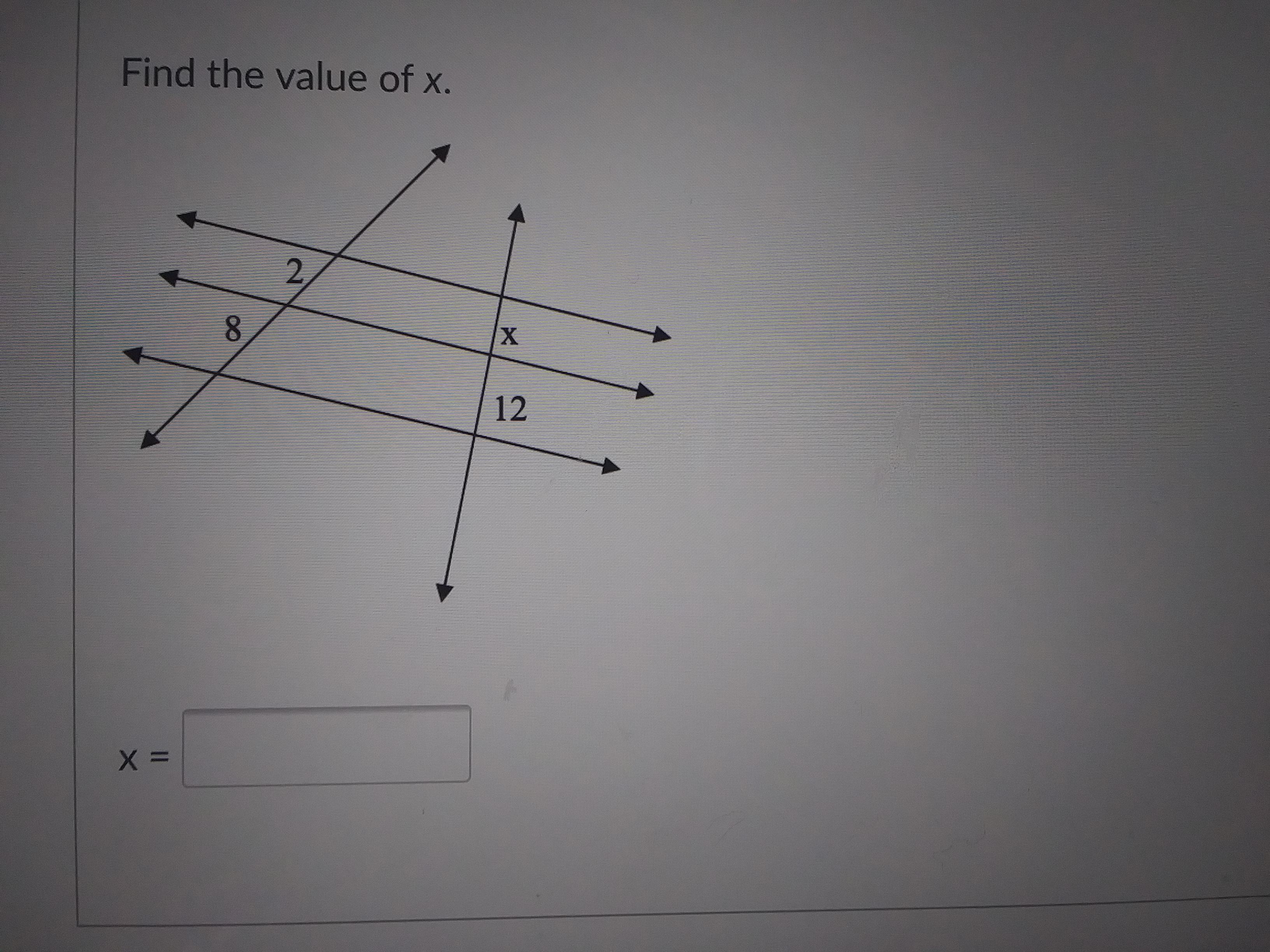


Answers
Answer:
#1
x/12 = 2/8x = 12/4x = 3#2
m∠E = 180° - (60° + 53°) = 67° ∠E ≅ ∠H ⇒ ∠D ≅ ∠GΔCDE ~ ΔFGH by AA postulate
#16
a = 3.5 in and k = 2/3, a' = ?a' = ak a' = 3.5*2/3 = 7/2*2/3 = 7/3 = 2 1/3 inCorrect choice is D
Please Help Due Today!!!!!
Identify the shape of a cross section of a pyramid, and describe how you would slice the pyramid to generate this shape.
Answers
Answer: 23 4 are
Step-by-step explanation:
square OABC is drawn on a centimetre grid. O is (1,3) A is (3,3) B is (3,5)
Answers
Answer:
you have to tell us the question honey
a washing machine can hold 3/4 kg of laundry in each load. if randy has . 6 kilograms of laundry, how many loads does he need to do? 5 6 7 d8
Answers
Randy needs 8 loads.
To find the answer on the question we have to follow the method of multiplication and division .
A washing machine can hold \(\frac{3}{4}\) kg of laundry in each load.
\(\frac{3}{4}\) kg of laundry is equal to 1 load.
\(\frac{3}{4}\) kg of laundry = 1 load
1 kg of laundry = \(\frac{1 * 4}{3}\) load ( following the method of division )
1 kg of laundry = \(\frac{4}{3}\) load
Randy has 6kg of laundry.
So, 1kg of laundry i.e \(\frac{4}{3}\) load is to be multiplied by 6.
6kg of laundry = \(\frac{4 * 6}{3}\) load ( following the method of multiplication)
= 8 loads
Hence, Randy needs 8 loads.
Read more about multiplication :
https://brainly.com/question/26669440
#SPJ4
If KK is the midpoint of \overline{JL}
JL
, JK=8x+11JK=8x+11, and KL=14x-1KL=14x−1, find JL.JL.
Answers
Answer:
JL = 54
Step-by-step explanation:
When K is the midpoint of JL, we have ...
JK + KL = JL
and
JK = KL
Using this latter equation, we can substitute the given expressions to get
(8x+11) = (14x -1)
12 = 6x . . . . . . . . . add 1-8x to both sides
2 = x
Using this, we can find JL.
JK = 8x +11 = 8(2) +11 = 27
KL = JK = 27
JL = JL +KL = 27 +27
JL = 54
how does attitude, beliefs and knowledge impact how a teacher delivers a lesson
Answers
Attitude, beliefs, and knowledge shape a teacher's delivery: attitude affects engagement, beliefs influence instructional decisions, and knowledge enables effective communication and learning facilitation.
Attitude, beliefs, and knowledge play crucial roles in shaping how a teacher delivers a lesson. Here's a detailed explanation of their impacts:
Attitude:
Attitude refers to a teacher's mindset, emotions, and approach towards teaching. A positive attitude fosters enthusiasm, motivation, and a genuine passion for the subject matter. This translates into an engaging and dynamic teaching style, creating an environment conducive to learning. Conversely, a negative attitude can lead to disinterest, lack of enthusiasm, and a disengaged teaching approach, which can hinder students' engagement and comprehension.
Beliefs:
A teacher's beliefs influence their instructional decisions and pedagogical strategies. Beliefs about students' capabilities, learning styles, and the purpose of education can shape the teacher's approach to delivering a lesson. For example, if a teacher believes that all students have the potential to succeed, they may employ differentiated instruction techniques to cater to diverse learning needs. Conversely, if a teacher holds limiting beliefs about students' abilities, they may adopt a one-size-fits-all approach, which may hinder student progress.
Knowledge:
A teacher's knowledge encompasses both subject matter expertise and pedagogical content knowledge. Profound knowledge of the subject allows a teacher to effectively structure and present the lesson, answer student queries, and provide relevant examples. Pedagogical content knowledge helps in selecting appropriate instructional strategies, adapting to student needs, and assessing learning effectively. Without a strong knowledge base, a teacher may struggle to deliver accurate information, engage students, or address misconceptions.
Collectively, attitude, beliefs, and knowledge significantly impact a teacher's delivery of a lesson. A positive attitude enhances student motivation and engagement. Strong beliefs in students' potential and individualized instruction foster a supportive learning environment. Adequate subject knowledge and pedagogical skills enable effective communication and facilitate meaningful learning experiences. By combining these elements, teachers can create an impactful and effective learning environment that nurtures student growth and achievement.
for such more question on learning facilitation.
https://brainly.com/question/23008798
#SPJ8
Given J(x, -8) and K(-1, -5) and the graph
of l line I below, find the value of x so that
JK || l.

Answers
The value of x for which the points j(x, -8) and K(-1, -5) is parallel to the line l is -2
What is an intercept?An intercept is any point on the graph where the line or curve touches the x or y axes.
If the intercept is on the y-axis the coordinate of x is 0 and if the intercept is on the x-axis the coordinate of y is 0.
For the line l, the coordinates of the marked points are (0, 2) and (-2, -4)
The slope of the line is \(\frac{y_{2} - y_{1} }{x_{2} - x_{1} }\)
\(x_{1}\) = 0, \(x_{2}\) = -2 , \(y_{1}\) = 2, \(y_{2}\) =-4
Slope of the line = -4 -2 / -2 - 0
slope = -6/-2
slope(P) = 3
slope(R) for the line formed by the two points J(x, -8) and K(-1, -5)
R = -5 - -8 / -1 -x
R = 3/-1 -x
For two parallel lines, their slopes are equal, that is
R = P
3/-1 -x = 3
By cross multiplying
3(-1 -x) = 3
-3 -3x = 3
-3x = 3 + 3
-3x = 6
x = 6/-3
x = -2
In conclusion, the value of x for which JK // l is -2
Learn more about parallel lines: https://brainly.com/question/26961508
#SPJ1
The length of a rectangle is three times the width. The perimeter of the rectangle is at most 112cm. Which inequality models the relationship between the width and the perimeter of the rectangle
Answers
Answer:
8x⩽112
Step-by-step explanation:
Width of the rectangle (in centimeters) = x
Therefore, the lenght of the rectable is 3x (in centimeters).
The perimeter of the rectangle (in centimeters) is : 2x+2*3x=2x+6x=8x.
The perimeter of the rectangle is at most 112cm, therefore, 8x⩽112.
Knowing the properties of a parallelogram solve for the value of y.
Show your work to receive full credit.

Answers
Find x first
Opposite sides of parallelogram are equal\(\\ \tt\hookrightarrow 9x-15=5x-3\)
\(\\ \tt\hookrightarrow 9x-5x=-3+15\)
\(\\ \tt\hookrightarrow 4x=12\)
\(\\ \tt\hookrightarrow x=3\)
Now
\(\\ \tt\hookrightarrow 3x-4=4y-2\)
\(\\ \tt\hookrightarrow 3(3)-4=4y-2\)
\(\\ \tt\hookrightarrow 9-4=4y-2\)
\(\\ \tt\hookrightarrow 4y-2=5\)
\(\\ \tt\hookrightarrow 4y=7\)
\(\\ \tt\hookrightarrow y=7/4\)
2) The ratio of adults to children in the sports club is 5:2.
There are 120 adults in the club. How many children are
there?
Answers
Answer:
48 children
Step-by-step explanation:
For every 5 adults there are 2 children.
so for every 1 adult there is 2/5 of a child.
So number of children = 120 * 2/5
= 240/5
= 48.
A cone has a height of 12 inches and a radius of 12 inches. What is its volume.

Answers
Answer:
1808.64 cubic inches is the answer

please do my last question u get more points if the answer is right. if inappropriate you get reported NO LINKS

Answers
Answer:
1.35!
Step-by-step explanation:
Its 1.35 dollars :). hope you get it right
Answer:
$1.35
Step-by-step explanation:
All you have to do is change 15% into a decimal by moving the decimal point two places left. so 15. moved two places left is 0.15
then multiply 0.15 times 9 and get 1.35
Circle the ratio which is the same as 1 cm represents 2m
1:2
1:20
1:200
1:2000
Answers
Answer:
1 cm: 200 cm (if they don't give units) (most likely this answer) (1:200)
if the units are centimeter and meter though, then it's
1:2
Step-by-step explanation:
there are 100 cm in 1 meter, so 1cm:2m
is actually 1cm : 200cm
The exact value of Tan 30 x sin 60
Answers
Answer:
\(\frac{1}{2}\)
Step-by-step explanation:
\(\tan \left(30^{\circ \:}\right)=\frac{\sqrt{3}}{3}\)
\(\quad \sin \left(60^{\circ \:}\right)=\frac{\sqrt{3}}{2}\)
\(=\frac{\sqrt{3}}{3}\times \frac{\sqrt{3}}{2}\)
\(=\frac{3}{6}\)
\(=\frac{1}{2}\)
Answer:
\(1/2\)
Step-by-step explanation:
Tan 30 = \(\frac{\sqrt{3} }{3}\)
Sin 60 = \(\frac{\sqrt{3} }{2}\)
Multiply the 2 roots you get my answer 1/2
michelle, a basketball player, has made 14 of her 20 free throws this season. if she never misses again, how many free throws would she need to shoot to have a shooting percentage of 90 percent?
Answers
Michelle would need to shoot an additional 40 free throws to have a shooting percentage of 90%.
Let's denote the number of additional free throws that Michelle needs to make as "x." Since she has made 14 out of her 20 free throws this season, her current shooting percentage is:
Current shooting percentage = (Number of made free throws / Total number of attempted free throws) * 100
= (14 / 20) * 100
= 70%
To find the number of additional free throws she needs to shoot to achieve a shooting percentage of 90%, we set up the following equation:
(14 + x) / (20 + x) = 90/100
We can now solve this equation to find the value of x:
(14 + x) / (20 + x) = 0.9
Cross-multiplying gives:
0.9 * (20 + x) = 14 + x
18 + 0.9x = 14 + x
0.9x - x = 14 - 18
-0.1x = -4
Dividing both sides by -0.1 gives:
x = 40
Therefore, Michelle would need to shoot an additional 40 free throws to have a shooting percentage of 90%.
To learn more about percentage click here:
brainly.com/question/23270628
#SPJ11
Consider a regular 52-card deck. if you pick a card randomly and then replace it 5 times, what is the probability of getting an ace exactly two times?
Answers
The fact that the cards are replaced means that the probability of picking an ace exactly two times after replacing the card 5 times is 0.47%
What is the probability of picking two aces?As the cards are replaced, this makes this an independent probabilities problem.
The probability of getting an ace exactly two times is:
= Probability of getting ace once x Probability of getting ace once x Probability of not getting ace³
Solving gives:
= 4/52 x 4/52 x (48/52)³
= 0.00465
= 0.47%
Find out more on probability at https://brainly.com/question/5858025
#SPJ4
PLS COME AND LOOK!!! I NEED YOU GENIUSES!!! I WILL GIVE BRAINLIEST!!!!! AT LEAST COME AND LOOK!!!! WILL FOREVER BE GREAT FULL!!! EASY IM JUST DUMB!!
Choose one value that is in the domain of both ( ) = 2and 2 = and that is greater than 0. Substitute that value into ( ) = 2and 2 = and then simplify. Explain how your answers help to show that the graph on the left represents a function while the graph on the right represents a relation. Show your work and use function notation where possible
(ignore the little checks on the graph lol)

Answers
Heres a Simple Answer:
1. The one on the left follows the Vertical Line test, while the one on the right doesn't
2. A function is either y = mx+b, or a Nonlinear function. The one on the right is a Parabolic Function becuase it has the x^2 on it. The right one is y^2, which is not a function.
(Not very good, but I gtg so I rushed.)
I Need Help again Pls fast

Answers
Answer:
The scale factor is 60
Step-by-step explanation:
The drawing is measured in inches and the billboard is measured in feet. First, convert 15 feet to 180 inches. Then use the ratio \(\frac{180}{3}\) to find that the scale factor is 60. This means the length of the billboard will be 600 inches or 50 feet.
1 2/5m-3/5(2/3m+1) How do you solve this problem
Answers
Step-by-step explanation:
I am not sure what you mean by "solve".
I assume you mean simplify the expression.
and then it is very tricky to find the true original expression the way you typed it.
I think you meant
1 2/(5m) - 3/(5(2/(3m + 1)))
1 = 5m/5m
1 2/(5m) = (5m+2)/5m
3/(5(2/(3m + 1))) = 3/(10/(3m + 1)) = 3/1 / (10/(3m + 1))
when dividing by a fraction, it is the same as multiplying with the upside-down fraction
so, this is the same as
3/1 × (3m + 1)/10 = (3(3m + 1)) / (10×1) = (9m + 3)/10
this would give us in total
(5m + 2)/5m - (9m + 3)/10
to do the subtraction we need to bring both fractions to the save denominator (lower part).
it seems to me the easiest one would be 10m.
so,
2×(5m + 2)/10m - m×(9m + 3)/10m =
= (10m + 4)/10m - (9m² + 3m)/10m =
= (10m + 4 - 9m² - 3m)/10m = (-9m² + 7m + 4)/10m
if we want to transform this back to a sum of fractions :
4/10m - (9m² - 7m)/10m = 2/5m - (9m - 7)/10
Peter walks to school each morning. One particular morning he found $10 on the ground. He
stopped at the store and used that money to buy 2 bags of Takis and a bag of Flamin' Hot
Cheetos. The Takis cost $1.79 per bag and the Cheetos cost $1.59. Later that day he bought a
school lunch for $3. He sold one of the bags of Takis to a friend for $2. On the way home he
gave his sister $1.50 to buy candy. What integer represents the money Peter has left from the
$10 he found that morning? *
Answers
Answer:
2.33
Step-by-step explanation:
if each of seven persons in a group shakes hands with each of the other six persons, then a total of forty-two handshakes occurs?
Answers
A total of 21 handshakes, will occur when seven persons in a group shake hands with each of the other six persons.
The first person shakes hands with the other 6 people. The second person shakes hands with 5 people because they already shook hands with the first person.
The third person shakes hands with 4 people because they already shook hands with the first and second person.
The fourth person shakes hands with 3 people because they already shook hands with the first, second, and third. The fifth person shakes hands with 2 people because they already shook hands with the first, second, third, and fourth person.
The sixth person shakes hands with the seventh person because the rest have already shaken hands with them. The seventh person doesn't have anyone else to shake hands with.
Add all the people who shake6+5+4+3+2+1
So the total would be 21
To know more about Probability:
https://brainly.com/question/13391136
#SPJ4
Match the expression to the exponent rule. One rule will not be used.

Answers
Answer:
Step-by-step explanation:
from top down:
xᵃ⁻ᵇ
xᵃ⁺ᵇ
1
xᵃˣᵇ
1/xᵃ
A profit maximising firm has a marginal cost function given by MC=6Q 2 −10Q+12 and a marginal revenue function given by MR=100−2Q i) Find expressions for the firm's Total Revenue and Total Cost functions in terms of Q. ii) Find the profit maximising level of output if the firm's fixed costs of production are zero. [30 marks]
Answers
i) The firm's Total Cost function is TC =\(2Q^3 - 5Q^2 + 12Q + C\), where C is the constant of integration representing fixed costs.
ii) The profit-maximizing level of output, when the firm's fixed costs are zero, is approximately 4.41 units.
i) To find the firm's Total Revenue (TR) function, we need to multiply the quantity (Q) by the price. In this case, the price is given by the marginal revenue function (MR).
Given that MR = 100 - 2Q, the total revenue can be calculated as:
TR = Q * MR
= Q * (100 - 2Q)
= 100Q - \(2Q^2\)
So, the firm's Total Revenue function is TR = 100Q - 2Q^2.
To find the firm's Total Cost (TC) function, we need to integrate the marginal cost function (MC) with respect to Q.
Given that MC = \(6Q^2 - 10Q + 12,\) the total cost can be calculated as:
TC = ∫(MC) dQ
\(= ∫(6Q^2 - 10Q + 12) dQ\)
\(= 2Q^3 - 5Q^2 + 12Q + C\)
So, the firm's Total Cost function is TC =\(2Q^3 - 5Q^2 + 12Q + C\), where C is the constant of integration representing fixed costs.
ii) To find the profit-maximizing level of output, we need to determine the quantity (Q) at which marginal cost (MC) equals marginal revenue (MR). In this case, MR is given by 100 - 2Q.
Setting MC equal to MR, we have:
MC = MR
\(6Q^2 - 10Q + 12 = 100 - 2Q\)
Simplifying the equation, we get:
\(6Q^2 + 8Q - 88 = 0\)
To solve this quadratic equation, we can use the quadratic formula:
\(Q = (-b ± √(b^2 - 4ac)) / (2a)\)
Applying the values a = 6, b = 8, and c = -88, we get:
\(Q = (-8 ± √(8^2 - 4*6*(-88))) / (2*6)\)
Q = (-8 ± √(64 + 2112)) / 12
Q = (-8 ± √2176) / 12
Since we are looking for a positive quantity, we take the positive square root:
Q = (-8 + √2176) / 12
Calculating this value, we find:
Q ≈ 4.41
Therefore, the profit-maximizing level of output, when the firm's fixed costs are zero, is approximately 4.41 units.
Learn more about quadratic equation here:
https://brainly.com/question/30098550
#SPJ11
Nina has one job babysitting another job walking dogs. Each week she babysits for 21 hours and walk stocks for nine hours Sharon $7.50 per hour for dog walking. She earns $1.50 more per hour for babysitting them for dog walking there are 4 1/2 weeks in the month of July. What is the best estimate for the total amount of money Nina earns in July.
Answers :
$250
$750
$1200
$1500
Answers
Answer:
The best estimate for her earnings is $1200
Step-by-step explanation:
Number of time spent babysitting each week = 21 hours = BBS
Number of time spent dog walking each week = 9 hours = DW
She earns $7.50 per hour for dog walking,
She earns $(7.50+1.50) = $9 for baby sitting,
There are 4 1/2 weeks = 9/2 weeks in July,
Now, for each week she earns 21(9) = $189 from baby sitting
and 9(7.5) = $67.5 from dog walking,
So, for the month of July, i.e. 9/2 weeks, she earns,
9/2(189) = $ 850.5 from baby sitting,
and (9/2)(67.5) = $303.75 from dog walking,
In total for the month, she earns,
850.5 + 303.75 = $1154.25
Hence the best estimate for her earnings is $1200
19. State all integer values of x in the interval [4, 10] that
satisfy the following inequality:
3x-3>12
Answers
The integer values of x that satisfy the inequality 3x - 3 > 12 are 6, 7, 8, 9, 10
Calculating the integer values in the intervalTo solve the inequality 3x - 3 > 12, we can isolate the variable x on one side of the inequality by adding 3 to both sides:
3x - 3 + 3 > 12 + 3
3x > 15
Next, we can divide both sides by 3 to get x by itself:
x > 5
So we know that any integer value of x in the interval [4, 10] that is greater than 5 will satisfy the inequality.
Therefore, the integer values of x that satisfy the inequality are:
6, 7, 8, 9, 10
Note that 5 is not included in this list, since the inequality is strict (i.e., x is greater than 5, not greater than or equal to 5).
Read more about inequality at
https://brainly.com/question/30390162
#SPJ1