Answers
Related Questions
You are riding your bike and notice the square sign above. You mentally draw a
straight line from point A to C. Describe the angle relationship between /_DCA and
/_BCA.

Answers
===========================================================
Explanation:
When using the SSS congruence rule, we can prove that triangle DCA is congruent to triangle BCA.
Since the triangles are congruent, the corresponding pieces angle DCA and angle BCA are equal in measure (if they weren't, then the triangles wouldn't be congruent).
Recall that any square has four right angles, ie all angles are 90 degrees each. Angle DCB is cut in half to get 90/2 = 45.
The angles DCA and DCB are 45 degrees each.
what is the slope and intercept of this equashion y = -9x + 3
Answers
Answer:
slope is -9
y intercept is 3
Step-by-step explanation:
its in the equation
26. My little brother has a 4-digit bike lock with the digits 0 to 9 on each part of the lock as shown. He started on the correct combination and turned each part the same amount in the same direction and now the lock shows the combination 6348. Which of the following CAN- NOT be the correct combination of my brother's lock? (A) 8560 (B) 3015 (C) 4906 (D) 1893 (E) 6348 0782 Activate Windows
Answers
Answer:
A
Step-by-step explanation:
The answer is option (A) 8560. This combination cannot be the correct combination for your brother's lock because it contains the digit '6' in the same position as the correct combination (6348), but the other digits do not match.
A small class has 9 students, 4 of whine are girls and 5 of whom are boys. Teacher is going to choose two of the students at random. What is the probability that the teacher will choose two girls? Write your answer as a fraction in simplest form.
Answers
The probability that the teacher will choose two girls would be = 1/6
What is probability?Probability is defined as the expression that shows the possibility of an outcome of an event which may or may not happen.
The total number of students in the class = 9
The total number of girls = 4
The total number of boys = 5
The formula for finding probability = No of favourable outcome/Total number of outcomes.
The probability that teacher choose first girl = 4/9
One girl is selected we must reduce the number of girls available for selection to 4 - 1 = 3.
We must also reduce the number of children available for selection 9 - 1 = 8.
The probability that teacher choose second girl = 3/8
Thus, the probability = 4/9 × 3/8 = 1/6
Learn more about probability here:
https://brainly.com/question/25870256
#SPJ1
If mZA = (4x - 2)° and mZB= (6x-20), what is the value of x?
Answers
To find the value of x, we can set the two angle measures equal to each other and solve for x.
Given:
mZA = (4x - 2)°
mZB = (6x - 20)°
Setting them equal to each other:
4x - 2 = 6x - 20
Now, we can solve for x:
4x - 6x = -20 + 2
-2x = -18
Dividing both sides by -2:
x = -18 / -2
x = 9
Therefore, the value of x is 9.
Answer:
The answer is 9.
Step-by-step explanation:
We need to use the fact that the sum of the angles in a triangle is 180 degrees. Let A, B, and C be the three angles in the triangle. Then we have:
mZA + mZB + mZC = 180°
Substituting the given values, we get:
(4x - 2)° + (6x - 20)° + mZC = 180°
Simplifying the left side, we get:
10x - 22 + mZC = 180°
Next, we use the fact that angles opposite congruent sides of a triangle are congruent. Since we know that segment AC and segment BC are congruent, we have:
mZA = mZB
Substituting the given values and simplifying, we get
4x - 2 = 6x - 20
Solving for x, we get:
x = 9
Therefore, the value of x is 9.
A fudge company makes 4 pounds of fudge. A worker separates the fudge into packages of ¼ of a pound of fudge each. How many packages does he make?
A 1/16
B 1
C 8
D 16
Answers
Answer:
16
Step-by-step explanation:
we are dividing based on the word separate.
4 divided by 1/4 is 16/1 which is 16.
so the worker made 16 packages
Please inform me if there are any questions:)
The number of fudge will be 16. The correct option is D.
What is an expression?The mathematical expression combines numerical variables and operations denoted by addition, subtraction, multiplication, and division signs.
Mathematical symbols can be used to represent numbers (constants), variables, operations, functions, brackets, punctuation, and grouping. They can also denote the logical syntax's operation order and other properties.
Given that a fudge company makes 4 pounds of fudge. A worker separates the fudge into packages of ¼ of a pound of fudge each.
We are dividing based on the word separate.
4 divided by 1/4 is 16/1 which is 16.
Number = 4 / ( 1 / 4 )
Number = 16
The worker made 16 packages.
To know more about an expression follow
https://brainly.com/question/15978558
#SPJ2
The ratio 81:108 in the simplest form
Answers
The ratio 81:108 can be simplified to 9:13. To find the simplest form of the ratio, you can divide both numbers by the greatest common factor. The greatest common factor of 81 and 108 is 9, so you can divide both numbers by 9 to get the simplified ratio of 9:13.
A punch recipe calls for 5 cups of watermelon juice for every 3 cups of grape juice. Select all the statements about the recipe that are correct. *
A : The ratio of grape juice to punch is 8:3.
B : The ratio of watermelon juice to grape juice is 5:2.
C : There are 5 cups of watermelon juice for every 8 cups of punch.
D : The ratio of grape juice to watermelon juice is 3 to 5.
Answers
Answer:
d
Step-by-step explanation:
Answer:
D B ?? i think this is correct
Step-by-step explanation:
Solve for k:
K/2 plus 1/2=3
Answers
Answer:v
vvre
Step-by-step explanation:
Answer:
K should be 5
Step-by-step explanation:
1/2 is .5 which leaves k/2 you need 2.5 to make three and 2.5*2 is 5 5/2 is 2.5 plus 5 is 3 therfore k is 5
how many square yards of carpet are needed to completely cover a rectangular floor that measures 15 feet by 9 feet?
Answers
Answer:
0.6
Step-by-step explanation:
Solve the given equation by completing the square.
Fill in the values of a, b, and e to complete the solutions.

Answers
The solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
How to solve quadratic equation?
To solve the equation x²+8x-38=0, we can use the quadratic formula:
x = (-b ± sqrt(b²-4ac)) / 2a
Here, a=1, b=8, and c=-38. Substituting these values into the formula gives:
x = (-8 ± sqrt(8²-4(1)(-38))) / 2(1)
x = (-8 ± sqrt(324)) / 2
x = (-8 ± 18) / 2
So x is either -13 or 5.
To find the values of x in the form of X = a + b√c and X = a - b√c, we can use the following steps:
For X=a+b√c:
Let's assume that x = a + b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a + b√c)² + 8(a + b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + 2ab√c + b²c) + 8a + 8b√c - 38 = 0
Separating the real and imaginary parts, we get:
(a² + b²c + 8a - 38) + (2ab√c + 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
First, setting the real part equal to zero gives:
a² + b²c + 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (-8 ± sqrt(8²-4(bc-38))) / 2
Simplifying this gives:
a = -4 ± sqrt(4+b(b-10))
Now, setting the imaginary part equal to zero gives:
2ab + 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c + 8a - 38 = a² + 8a - 38 = 0, which has roots a = -5 and a = 3. Therefore, the solution in this case is x = -5 or x = 3, which cannot be expressed in the form of X = a + b√c.
If b = -4, then a² + b²c + 8a - 38 = a² + 16c + 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = -4 ± sqrt(102-4c)/2
Therefore, the solution in this case is x = (-4 + sqrt(102-4c))/2 - 4√c, which can be expressed in the form of X = a + b√c.
For X=a-b√c:
Using the same logic, we can assume that x = a - b√c, where a, b, and c are constants to be determined.
Substituting this into the original equation x²+8x-38=0, we get:
(a - b√c)² + 8(a - b√c) - 38 = 0
Expanding the square and simplifying, we get:
(a² + b²c - 8a - 38) + (-2ab√c - 8b)√c = 0
Since the real and imaginary parts of the equation must both be zero, we can set them each equal to zero and solve for a, b, and c.
Setting the real part equal to zero gives:
a² + b²c - 8a - 38 = 0
This is a quadratic equation in a, so we can use the quadratic formula:
a = (8 ± sqrt(8²+4(bc+38))) / 2
Simplifying this gives:
a = 4 ± sqrt(4+b(b+10))
Setting the imaginary part equal to zero gives:
-2ab - 8b = 0
Solving for b, we get:
b = 0 or b = -4
If b = 0, then a² + b²c - 8a - 38 = a² - 8a - 38 = 0, which has roots a = -3 and a = 11. Therefore, the solution in this case is x = -3 or x = 11, which cannot be expressed in the form of X = a - b√c.
If b = -4, then a² + b²c - 8a - 38 = a² + 16c - 8a - 38 = 0. Plugging this into the quadratic formula for a, we get:
a = 4 ± sqrt(102+4c)/2
Therefore, the solution in this case is x = (4 + sqrt(102+4c))/2 - 4√c, which can be expressed in the form of X = a - b√c.
To know more about Equation visit :-
https://brainly.com/question/22688504
#SPJ1
when using the some rule ,we only use two of the equal ratios at one time.That is we work with pairs of _____ sides and angle?
Answers
When applying the some rule, we only combine two equal ratios at once. Consequently, we deal with pairs of sides and angles that have equivalent ratios.
Which set of ratios form a proportion?When two ratios are equal, a percentage is formed; alternatively, two equal ratios can be said to produce a proportion. When we understand that two ratios are equal, you can write a proportion. The ratios of these two numbers are equal.
When two variables are correlated in a manner that their ratios are equal, this is known as a proportional relationship. In a proportional connection, one variable is always a constant value multiplied by the other, which is another way to think of them. The "constant of proportionality" is the term used to describe that constant. Two angles are said to be complimentary if their sum is 90 degrees. Alternatively put, two angles are said to be complimentary if they combine to make a right angle.
To learn more about ratio refer to :
https://brainly.com/question/2328454
#SPJ1
PLEAS HELP!!! The function f(x) = 500(0.75)^x represents the amount of a 500-mg dose of
medication remaining in a patient's system x number of hours from the time the patient
took the medication. Which percent is the rate of decrease of the medication?
A. 75%
B. 25%
C. 7.5%
D. 2.5%
Answers
the answer is b
cccxcxcxcxcxzczczxc
The percentage of the rate of decrease in the medication will be 75%. Option A is correct.
What is an exponential function?The exponential function is characterized as a function that increases quickly and whose value is always positive. With the exponent y = aˣ, where a is the constant and a>1.
It is given that the function is,f(x) = 500(0.75)ˣ. The number x represents the number of hours since the patient took their medication.
f(x) = 500(0.75)ˣ
Compare the function with the standard function as
y=baˣ
Where b is the constant value, a is the percent of the rate of decrement and x is the time period,
The value of a for the given function will be 0.75. The value is in percentage form and can be written as,
=0.75 ₓ 100
=75%
Thus, the medication's rate of decline will be 75%. Option A is correct.
Learn more about the exponential function here:
brainly.com/question/11487261
#SPJ2
If the statement 4 > 3 is true, which of the following are true about the relationship between –4 and –3? Check all that apply.
–4 < –3
The inequality changes from greater than to less than because -4 is less than -3.
–4 > –3
The greater than inequality holds true even when the opposites of 4 and 3 are used.
–4 = –3
Answers
Answer:
A AND B
Step-by-step explanation:
TRUST MEEEEE FRENZ:)
If 4 > 3 then - 4 < -3 is true because when additive opposites of numbers are used inequality get reversed.
What is an inequality?Inequality refers to a relationship that makes a non-equal comparison between two numbers or other mathematical expressions.
Given inequality,
4 > 3
If we multiply with -1 on both sides inequality get reversed
-1 × 4 > -1 × 3
-4 < -3.
Hence, the inequality changes from greater than to less than when opposites of 4 and 3 are used.
Learn more about inequality here:
https://brainly.com/question/30231190.
#SPJ6
write each info entire radical √48
Answers
The value of the radical √48 is 4√3.
Radical is a symbol (√) that denotes square roots and nth roots. The number inside the symbol is called Radicand and the expression containing the radical or a square root is called a Radical expression.
Here, we are given the radical √48
To find the value of the radical, we will factorize 48
i.e., 48 = 2×2×2×2×3
= 16×3
Now, the square root of 48, that is, √48
= \(\sqrt{16\cdot3}\) =\(\sqrt{16} \cdot \sqrt{3}\)
We know 16 is a perfect square of 4, that is, the square root of 16= 4
⇒√16=4
Using this, we have √48= 4√3
The correct answer is 4√3.
Learn more about radicals here:
https://brainly.com/question/12739054
#SPJ1
Find the measure of c.

Answers
Answer:
100°
Step-by-step explanation:
basically, in this situation, whatever number or angle you're given, and the number diagonally across from it are supposed to add up to 180°.
(i think its called a cyclic quadrilateral, so do with that what you will.)
Convert 26.00 kilometers into miles. Express your answer as decimal rounded to two places,
Answers
Answer:
16.20 milesStep-by-step explanation:
Convert 26.00 kilometers into miles. Express your answer as decimal rounded to two places,
1 Km = 0,621371 Miles
so
26 * 0,621371 = 16,155646 miles
round
16.20
find the values of x and y that maximize the objective function c = 3x + 4y for the graph
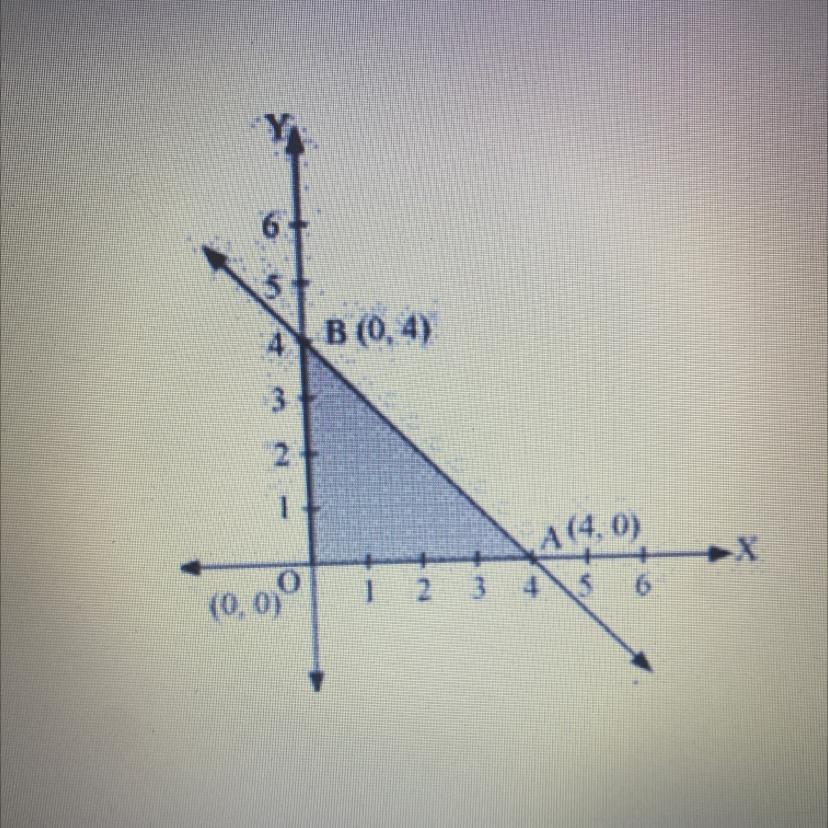
Answers
Answer: The correct answer is x=0 and y=4 or (0,4) per the graph
Step-by-step explanation:
To find the maximum value, we must test each point using the equation:
Check for (0,4):
C=3x+4y
C=3(0)+4(4)
C=16
Check for (2,2):
C=3(2)+4(2)
C=6+8
C=14
Check for (4,0):
C=3(4)+4(0)
C=12
Answer:
Step-by-step explanation:
By using graphical method, find optimal solution of the problem max z = 3x + y s.t 2x - y ≤ 5 -x + 3y ≤ 6 x ≥ 0, y ≥ 0
Answers
By analyzing the graph and evaluating the objective function at each vertex of the feasible region, we can find the optimal solution, which is the vertex that maximizes the objective function z = 3x + y.
To find the optimal solution of the given problem using the graphical method, we need to plot the feasible region determined by the given constraints and then identify the point within that region that maximizes the objective function.
Let's start by graphing the constraints:
1. Plot the line 2x - y = 5. To do this, find two points on the line by setting x = 0 and solving for y, and setting y = 0 and solving for x. Connect the two points to draw the line.
2. Plot the line -x + 3y = 6 using a similar process.
3. The x-axis and y-axis represent the constraints x ≥ 0 and y ≥ 0, respectively.
Next, identify the feasible region, which is the region where all the constraints are satisfied. This region will be the intersection of the shaded regions determined by each constraint.
Finally, we need to identify the point within the feasible region that maximizes the objective function z = 3x + y. The optimal solution will be the vertex of the feasible region that gives the highest value for the objective function. This can be determined by evaluating the objective function at each vertex and comparing the values.
Note: Without a specific graph or additional information, it is not possible to provide the precise coordinates of the optimal solution in this case.
For more such questions on graph
https://brainly.com/question/19040584
#SPJ8
The formula for the volume of a sphere is V = 4/3 pie3 . What is the formula solved for r ?
Answers
The formula for the radius (r) of a sphere, given the volume (V), is \(r = \sqrt[3]{ \frac{3V} {4\pi} }\).
To solve the formula for the volume of a sphere, \(V = \frac 43 \pi r^3\), for r, we'll follow these steps:
1. Begin with the formula for the volume of a sphere: \(V = \frac 43 \pi r^3\).
2. Multiply both sides of the equation by (3/4) to isolate π\(r^3\):
\(\frac34V = \pi r^3\).
3. Divide both sides of the equation by π to obtain the expression for r^3:
\(r^3 = \frac34 \frac V\pi\).
4. To solve for r, take the cube root of both sides of the equation:
\(r = \sqrt[3]{ \frac{3V} {4\pi} }\).
Therefore, the formula solved for r is \(r = \sqrt[3]{ \frac{3V} {4\pi} }\). This formula allows you to calculate the radius of a sphere when the volume (V) is given.
For more questions on an equation
https://brainly.com/question/29174899
#SPJ8
Solve the system.
x – y + z = 14
y +z = 15
z = 7
=
Enter your answer as an ordered triple.
([ ? ],[],[])
Answers
Answer:
(15, 8, 7 )
Step-by-step explanation:
x - y + z = 14 → (1)
y + z = 15 → (2)
z = 7 ← value of z is given
Substitute z = 7 into (2)
y + 7 = 15 ( subtract 7 from both sides )
y = 8
Substitute y = 8, z = 7 into (1)
x - 8 + 7 = 14
x - 1 = 14 ( add 1 to both sides )
x = 15
solution is (15, 8, 7 )
Q - Determinate the value of the following expression:
\(\frac{\sqrt{36} - \sqrt[3]{8} - \sqrt{144}}{\sqrt[3]{-64} + \sqrt[3]{125} } -1\)
Answers
The value of the given expression is - 9.
The square root of a number:
The square root of a number is a value that, when multiplied by itself, gives the original number.
For example, the square root of 25 is 5, because 5 x 5 = 25.
The symbol used to denote the square root of a number is √, and it is placed in front of the number.
For example, the square root of 25 can be written as √25.
Here we have
\(\frac{ \sqrt{36} - \sqrt[3]{8} - \sqrt{144} }{\sqrt[3]{-64} \sqrt[3]{125}} - 1\)
As w know,
36 = 6 × 6 = 6²
8 = 2 × 2 × 2 = 2³
144 = 12 × 12 = 12²
-64 = - 4 × -4 × -4 = (-4)³
125 = 5 × 5 × 5 = 5³
Hence, the above expression can rewrite as follows
\(\frac{ \sqrt{36} - \sqrt[3]{8} - \sqrt{144} }{\sqrt[3]{-64}+ \sqrt[3]{125}} - 1 = \frac{ \sqrt{ 6^{2} } - \sqrt[3]{ 2^{3} } - \sqrt{12^{2} } }{\sqrt[3]{ (-4)^{2} }+ \sqrt[3]{5^{3} }} - 1\)
= \(\frac{ 6 - 2 - 12 }{ -4 + 5} - 1\)
= \(\frac{ -8 }{ 1} - 1\)
= -9
Therefore,
The value of the given expression is - 9.
Learn more about Square roots at
https://brainly.com/question/28156082
#SPJ1
How do i solve it with steps pls

Answers
Answer:
Step-by-step explanation:
We know the the total of angles for a triangle is 180 degrees.
So in this case we'd want to set up adding all of our angles and setting them equal to 180
17 + 126 + b = 180
then solve for b
143 + b = 180
b = 37 degrees
So the answer would be 37 degrees for angle b
Rocko paid 12.50 for 25 game tickets
Answers
He paid each game ticket for 0.5$
EXPLANATION
12.5/25
∠DGC and ∠CGB are □ angles.
Adjacent
Complementary
Supplementary
Vertical

Answers
Answer:
angle DGC and angle CGB are adjacent angles
Never mind i got it!
Answers
Answer:
OOk
Step-by-step explanation:
fine the value of X if angles ABC is Supplementary to CBD
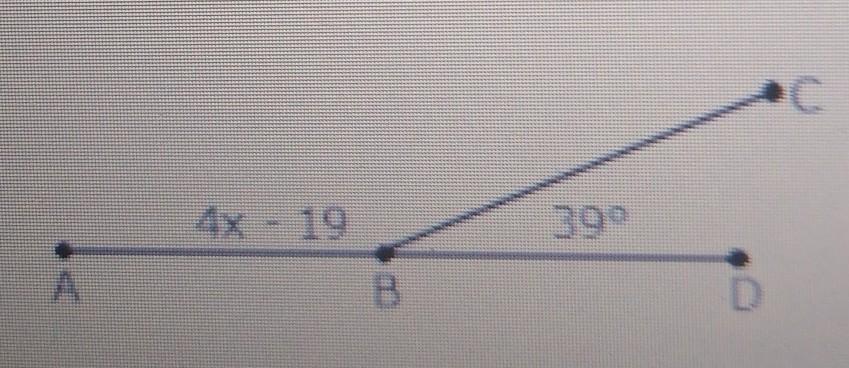
Answers
Two angles are called supplementary when their measures add up to 180 degrees..
Therefore, we have,
\(<\text{ABC}+<\text{CBD}=180\)Substituting the values we get,
\(\begin{gathered} 4x-19+39=180 \\ 4x+20=180 \\ 4x=180-20=160 \\ 4x=160 \\ x=\frac{160}{4}=40 \end{gathered}\)Thus, the required value of x = 40
Which number label represents the nucleus? O 5 3 O 2

Answers
A quiz consists of multiple choice questions. each question has 4 possible answers (a-d) and only one answer is correct. if the student guesses the answer to each question, then what is the probability that the student answer correctly for that question?
Answers
Answer:
Answers - 4
Correct Answer - 1
Probability - 1/4
Which number(s) have a 5 that is 10 times the value of the 13,725 in ?
Answers
Answer:
I will give you three, but the answer is the number that has a 50
Step-by-step explanation:
52
654
7657
50 is the numbers that have a 5 in 10 times the value of the 13,725.
What is place value?Place value is the value of each digit in a number.
For example, the 5 in 350 represents 5 tens, or 50; however the 5 in 5006 represents 5 thousands, or 5000.
Now the given number is,
13,725
10 times of the number is givens as,
13,725*10
or, 137,250
here place value of 5 in 137,250 is 5 tens or 50.
Therefore, 50 is the numbers that have a 5 in 10 times the value of the 13,725.
More about place value :
https://brainly.com/question/27733929
#SPJ1
