I need help with this question ASAP please!!!
At Lewisville University, they are looking into how often students
attend football games. Here are the results:
● 45% of students regularly attend football games
● Of those that attend football games regularly, 35% are first-year
students and 64% are upper-class students.
● Of those that do not attend football games, 25% are first-year
students and 34% are upper-class students
What is the approximate probability that a randomly selected person
will be attending the football game given they are an upper-class
student?
Answers
Answer:
60.63%
Step-by-step explanation:
Prob. of students who regularly attend = 45%
Prob. of students who don't attend = 55%
Upper Class Students who attend = 64 % of 45 %
= 0.64 × 0.45 × 100 = 28.8% = 0.288
Upper Class Students who don't attend = 34 % of 55% = 0.34 × 0.55 × 100 = 18.7% = 0.187
Total for Upper Class Students = 28.8% + 18.7% = 47.5% = 0.475
Probability that an Upper Class Student randomly selected will be attending = ( 0.288 / 0.475 ) × 100 = 0.6063 × 100 = 60.63%
Related Questions
help for 17 points.
Easy

Answers
The exponential function that represents the table is \(y =2\times 2^x\)
What is an exponential function?An exponential function is any function that has its constant raised to the power of an argument.
An exponential function is represented as:
\(y = ab^x\)
Where:
a represents the initial valueb represents the rateFrom the table we have the following ordered pair
(x,y) = {(0,2) (1,8)}
So, we have:
\(y = ab^x\)
\(2 = a \times b^0\)
\(a = 2\)
Also, we have:
\(y = ab^x\)
\(8 = 2 \times b^1\)
\(8 = 2 \times b\)
Divide both sides by 2
\(b =4\)
So, we have:
\(y = ab^x\)
\(y =2\times 2^x\)
Hence, the exponential function is:
\(y =2\times 2^x\)
Read more about exponential functions at:
brainly.com/question/11464095
Maria is 6 years older than her sister Emily. Emily is 15 years old. If M= Maria's age, then the equation M-6=15 would describe the problem. What inverse or opposite operation would you use to solve the equation?
A. Add 6 to both sides
B. Subtract 6 from both sides
C. Multiply both sides by 6
D. Divide both sides by 6
Answers
a local ice cream shop has a special deal on thursdays: buy a waffle cone for $3 and get each scoop of ice cream for $1.50. what would be the rate of change in this word problem?
Answers
In the given word problem, the rate of change is the change in the cost of the ice cream concerning the change in the number of scoops.
That is, the rate of change is the ratio of the change in the cost of ice cream and the change in the number of scoops. Let's first calculate the initial rate of change or slope of the given deal: When we buy a waffle cone, the cost is $3, and we can buy one scoop of ice cream for $1.50.So, for one scoop of ice cream, the total cost would be 3 + 1.50 = $4.50.
We can represent the cost of one scoop of ice cream with the help of a linear equation: y = mx + b. Here, the slope or the rate of change, m = Change in cost of ice cream/ Change in the number of scoops= 1.5/1= 1.5Therefore, the rate of change of the ice cream with respect to the number of scoops is $1.50/scoop.
To know more about linear equation refer to:
https://brainly.com/question/2030026
#SPJ11
Help me pls!!!!!!!!!!!!!!!

Answers
To solve this problem you can set up a proportion (I like doing it this way) or you can just do:
First deal:
(24/3)*5 = 40 dollars
Second deal:
(24/4)*6 = 36 dollars
Finding money saved:
40-36 =4
They will save 4 dollars buying the second 4 for 6 dollars deal!
how many decimal places of pi did hiroyoki gotu memorize in 1995?
Answers
Answer:
42,195
Step-by-step explanation:
Question 1 (2 points) The total distance in centimeters a toy robot moves varies directly with the time in seconds. The toy robot moves a total distance of 264 centimeters in 11 seconds. a. What is the time in seconds the toy robot moves when the total distance is 408 centimeters? Seconds b. What is the distance in centimeters the toy robot moves after 3 seconds? Centimeters
Answers
Answer:
a. \(T = 17s\)
b. \(D = 72cm\)
Step-by-step explanation:
Given
Direct Variation
\(Distance(D)\ \alpha\ Time (T)\)
D = 264 cm when T = 11 s
Calculating (a)
First, the constant of variation (k) as to be calculated;
Since, there exist a direct proportion; then,
\(D\ \alpha\ T\)
\(D = kT\)
Make k the subject of formula
\(k = \frac{D}{T}\)
D = 264 cm when T = 11 s; So
\(k = \frac{264}{11}\)
\(k = 24\)
So: Solving for (a)
\(D = 408\)
Substitute 408 for D and 24 for k in \(D = kT\)
\(408 = 24 * T\)
Divide both sides by 24
\(\frac{408}{24} = T\)
\(T = \frac{408}{24}\)
\(T = 17s\)
Hence, time to move a distance of 408cm is 17s
Calculating (b)
\(T = 3\)
Substitute 3 for T and 24 for k in \(D = kT\)
\(D = 24 * 3\)
\(D = 72cm\)
Hence, distance covered in 3 seconds is 72cm
Given a collection of 2023 closed squares of total area 4, prove that they can be arranged to cover a unit square (overlaps are allowed)
Answers
We can arrange the 2023 squares to cover the unit square, with overlaps allowed.
We can prove that a collection of 2023 closed squares of total area 4 can be arranged to cover a unit square by using the pigeonhole principle. Since the total area of the squares is 4, the average area of each square is 4/2023. Let's take a unit square and divide it into 2023 smaller squares of area (1/2023) each. By the pigeonhole principle, we can assign one of the 2023 squares to each of the smaller squares. Since the average area of each square is 4/2023, each of the assigned squares will overlap with at most 4 other squares. Therefore, we can arrange the 2023 squares to cover the unit square, with overlaps allowed.
Learn more about the pigeonhole principle here: brainly.com/question/30322724
#SPJ4
can you Identify the initial amount a and the growth factor b in the exponential function g(x) = 14 × 2x ?
Answers
The initial amount, a, in the exponential function g(x) = 14 × 2x is 14, and the growth factor, b, is 2.
This can be determined by looking at the equation and noting that the coefficient of x is 2, which indicates that the base of the exponential is 2. We can also calculate the initial amount and growth factor mathematically.
To calculate the initial amount, a, we can take the equation g(x) = 14 × 2x and set x = 0, yielding g(0) = 14 × 20, which simplifies to 14. To calculate the growth factor, b, we can take the natural log of both sides of the equation to yield ln(g(x)) = ln(14 × 2x).
Simplifying this gives
ln(g(x)) = ln(14) + ln(2x).
We can then divide both sides by x to yield
ln(g(x))/x = ln(14) + ln(2)/x.
We can then take the limit as x approaches 0, which yields
ln(g(0))/0 = ln(14) + ln(2)/0.
This simplifies to
ln(g(0)) = ln(14) + ln(2), which can be rearranged to
ln(2) = ln(g(0)) - ln(14).
Taking the exponential of both sides gives us
2 = e^(ln(g(0)) - ln(14)), which simplifies to
2 = g(0)/14, or b = g(0)/14 = 2.
This shows that the initial amount, a, is 14, and the growth factor, b, is 2.
Learn more about exponential function:
https://brainly.com/question/30241796
#SPJ4
Find the total area bounded by the x-axis and the curve y=f(x) on the indicated interval. Enter your answer in exa iorm or as a decimal number rounded to the nearest thousandth. f(x)=8x 2+6x+6;[−3,1]
Answers
The area bounded by the x-axis and the curve y = f(x) = 8x^2 + 6x + 6 on the interval [-3,1] is 73/3 square units. To find the area, the function was integrated using the absolute value of f(x) and split into two intervals.
To find the area bounded by the x-axis and the curve y = f(x) = 8x^2 + 6x + 6 on the interval [-3,1], we need to integrate the absolute value of the function f(x) with respect to x:
A = ∫[-3,1] |f(x)| dx
Substituting f(x) into the integral, we get:
A = ∫[-3,1] |8x^2 + 6x + 6| dx
To evaluate this integral, we need to split the interval into two parts: [-3,0] and [0,1], because the function f(x) changes sign at x = 0.
On the interval [-3,0], the absolute value of the function is:
|8x^2 + 6x + 6| = -(8x^2 + 6x + 6)
∫[-3,0] |8x^2 + 6x + 6| dx = -∫[-3,0] (8x^2 + 6x + 6) dx
= -27
On the interval [0,1], the absolute value of the function is:
|8x^2 + 6x + 6| = 8x^2 + 6x + 6
∫[0,1] |8x^2 + 6x + 6| dx = ∫[0,1] (8x^2 + 6x + 6) dx
= 28/3
Therefore, the total area bounded by the x-axis and the curve y = f(x) on the interval [-3,1] is:
A = ∫[-3,1] |f(x)| dx = ∫[-3,0] |8x^2 + 6x + 6| dx + ∫[0,1] |8x^2 + 6x + 6| dx
= -27 + 28/3
= -73/3
Since the area cannot be negative, we take the absolute value of the result:
|A| = 73/3
Therefore, the total area bounded by the x-axis and the curve y = f(x) on the interval [-3,1] is 73/3 square units.
To know more about area bounded by the curve, visit:
brainly.com/question/13252576
#SPJ11
Convert to slope intercept form
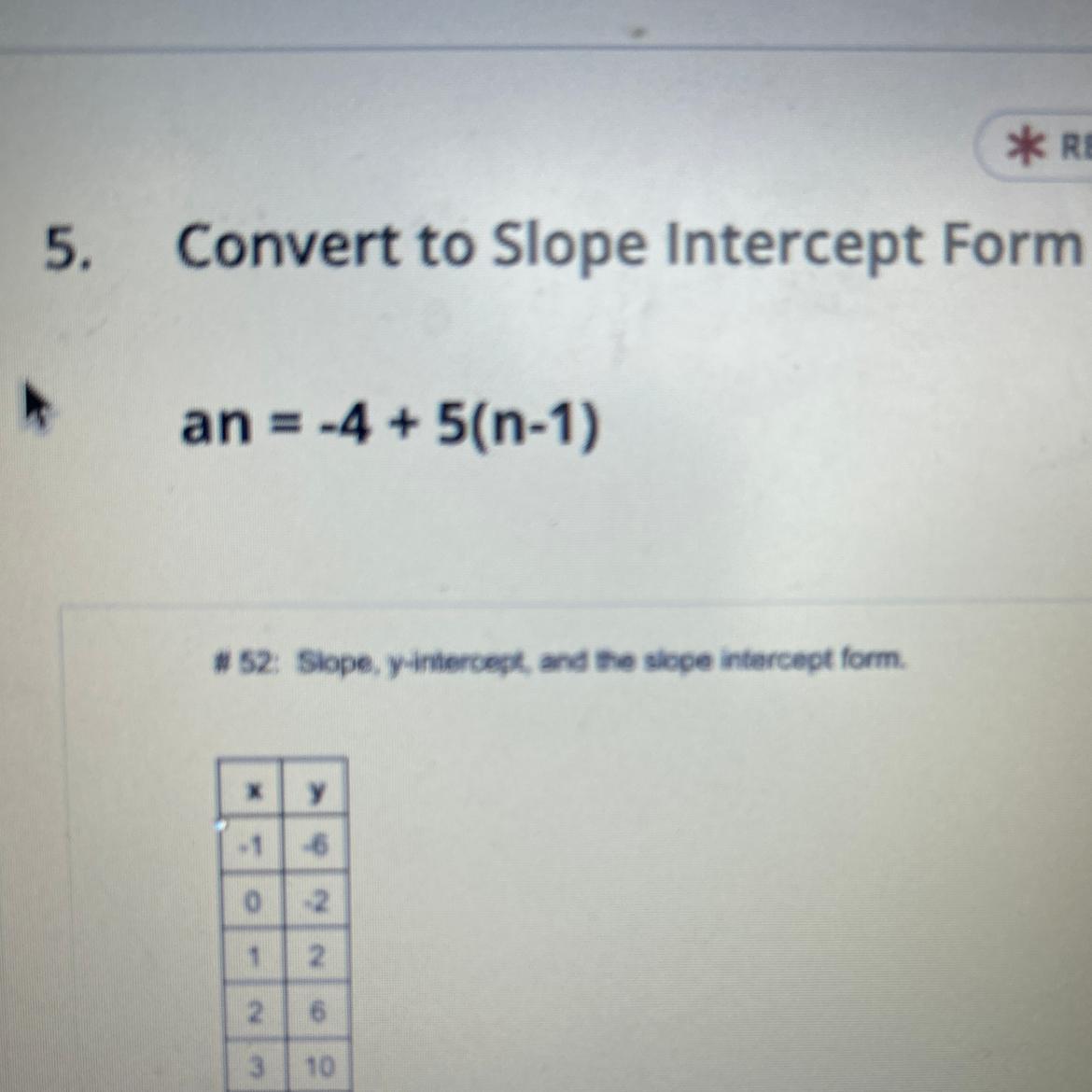
Answers
The function an = -4 + 5(n - 1) in slope intercept form is an = 5n - 9
How to rewrite the equation in slope intercept formFrom the question, we have the following parameters that can be used in our computation:
an = -4 + 5(n - 1)
The slope-intercept form of a linear equation is represented as
an = mn + c
Where the variable m is the slope and the variable c is the y-intercept
So, the first step in solving the question is to open the bracket in an = -4 + 5(n - 1)
This gives
an = -4 + 5n - 5
Add -5 and -9
an = 5n - 9
Hence, the representation of the equation is an = 5n - 9
Read more about linear equation at
https://brainly.com/question/14323743
#SPJ1
g etween two variables may be explained away by the presence of another variable that accounts for the original correlation. These relationships are known as
Answers
A spurious correlation is a correlation between two variables that appears to be causally linked but is actually due to the influence of a third variable that is not considered. The correct answer is spurious correlation.
Spurious correlations are correlations that exist between two variables, but they are not actually causally related to one another, despite the fact that they appear to be causally related at first glance. The relationship between two variables may be accounted for by a third variable that was previously overlooked or not considered, causing the original correlation to be explained away. Spurious correlations are commonly found in science and research, and they can lead to misleading results if not properly identified and accounted for. It is critical to account for all potential confounding variables in order to establish causal links between variables and avoid spurious correlations. Therefore, researchers must carefully consider all variables that might influence the relationship between two variables to avoid drawing inaccurate conclusions.
know more about spurious correlation
https://brainly.com/question/29361770
#SPJ11
a transformation is applied to a figure to create a new figure on a coordinate grid. which transformation does not preserve congruence?
Answers
Dilation does not preserve congruence, as it changes the size of the figure while keeping the same overall shape.
A transformation that does not preserve congruence is a dilation. A dilation is a transformation that changes the size of a figure while keeping the same overall shape. The formula for dilation is:
D(x,y)=(kx,ky)
Where k is the scale factor. A scale factor of less than 1 will decrease the size, whereas a scale factor greater than 1 will increase the size.
For example, if we have a triangle ABC with vertices A(1,1), B(3,3) and C(4,1), after dilation with a scale factor of 0.5, the vertices of the new triangle A'B'C' will be A'(0.5,0.5), B'(1.5,1.5) and C'(2,0.5).
As can be seen from the example, dilation does not preserve congruence. The triangle A'B'C' is not congruent to triangle ABC, since the length of the sides and the angles have changed.
Dilation does not preserve congruence, as it changes the size of the figure while keeping the same overall shape.
Learn more about congruence here:
https://brainly.com/question/7888063
#SPJ4
m divided by 19 = -2
(Find m)
Answers
Can u give me the brainliest ^^ plz ☺️☺️
What would be the best method to solve
the system of equations below?
6x + 3y = 21
2x – 3y = -13
Answers
You can isolate the y value by subtracting the x to the other side. All the numbers have 3 in common, so you need to divide all of them by 3. I would then substitute the new equation into the 2x-3y=-13, making it 2x-3(-2x+7)=-13
You wove the equation, and once you get your x value, you needles to substitute it in the equation: y=-2x+7
The final answers will be x=1 and y=5

Elimination method is the best method to solve the system of equations below
What is Equation?Two or more expressions with an Equal sign is called as Equation.
The given system of equations
6x + 3y = 21...(1)
2x – 3y = -13...(2)
Add equations (1) and (2)
6x+3y+2x-3y=21-13
8x=8
Divide both sides by 8
x=1
Now plug in x value in equation 1
6+3y=21
Subtract 6 from both sides
3y=15
Divide both sides by 3
y=5
By Elimination method we find the values of x and y.
Hence, Elimination method is the best method to solve the system of equations below
To learn more on Equation:
https://brainly.com/question/10413253
#SPJ2
I need help finding the slope (run,rise) of this graph.

Answers
5. Bob has utility over hammers (h) and dollars (m). U=v(3c
h
−3r
h
)+v(c
d
−r
d
) where v(x)=x for x≥0 and v(x)=2x for x≤0. (a) Assume that Bob's reference point is 0 hammers and 0 dollars. For each of the following choices, show Bob's expected utility for each option, and state which choice he would make. i. Would Bob choose Option A: 50% chance to win 16 hammers and 50% chance to win 4 hammers or Option B: definitely winning 8 hammers? ii. Would Bob choose Option A: 50% chance to lose 16 hammers and 50% chance to lose 4 hammers or Option B: definitely losing 12 hammers? iii. Would Bob choose Option A: 50% chance to gain 8 hammers and 50% chance to lose 4 hammers or Option B: gain 1 hammer. (b) Again, assume that Bob's reference point is 0 hammers and 0 dollars. Bob is offered the opportunity to buy a hammer for $2. - What would be Bob's utility if he does buy the hammer? - What would be Bob's utility if he does not buy the hammer? - Would Bob prefer to buy the hammer or not? 2 (c) Now assume that Bob recently received a hammer as a gift, and he has updated his reference point to be 1 hammer and 0 dollars. Bob is offered the opportunity to sell his hammer for $2. - What would be Bob's utility if he does sell the hammer? - What would be Bob's utility if he does not sell the hammer? - Would Bob prefer to sell the hammer or not? (d) Is Bob's buying price the same as his selling price? Describe one study discussed in class that demonstrates a similar concept.
Answers
To determine Bob's expected utility for each option, we calculate the utility for each outcome and weigh them by their respective probabilities.
Option A:
Expected utility = 0.5v(316 - 30) + 0.5v(4 - 0)
= 0.5v(48) + 0.5v(4) = 0.548 + 0.54 = 26.
Option B: Expected utility = v(8) = 8.
Bob would choose Option A as it has a higher expected utility.
ii. Option A: Expected utility = 0.5v(-16) + 0.5v(-4) = 0.5*(-32) + 0.5*(-8)
= -20.
Option B: Expected utility = v(-12) = -24. Bob would choose Option B as it has a higher expected utility.
iii. Option A: Expected utility = 0.5v(8) + 0.5v(-4) = 0.58 + 0.5(-8) = 0. Option B: Expected utility = v(1) = 1. Bob would choose Option B as it has a higher expected utility.
(b) If Bob buys the hammer for $2, his utility would be v(-2) = -4. If he does not buy the hammer, his utility would be v(0) = 0. Bob would prefer not to buy the hammer since the utility is higher at 0.
(c) If Bob sells the hammer for $2, his utility would be v(2) = 2. If he does not sell the hammer, his utility would be v(0) = 0. Bob would prefer to sell the hammer since the utility is higher at 2. (d) Bob's buying price is not the same as his selling price.
This concept is known as loss aversion, where individuals tend to value losses more than equivalent gains. One study that demonstrates a similar concept is the "Prospect Theory" by Daniel Kahneman and Amos Tversky, which shows how people's decision-making is influenced by the potential for gains and losses and how they weigh them differently.
The study revealed that individuals are generally more averse to losses and are willing to take greater risks to avoid losses compared to the risks they are willing to take for potential gains of equal value.
To learn more about probabilities click here: brainly.com/question/32004014
#SPJ11
please solve asap in my math final
find the value of x show ur work

Answers
Answer:
Step-by-step explanation:
43 + 24 + 57 + x = 180 degree (being sum of interior angles of a triangle)
124 + x = 180
x = 180 - 124
x = 56 degree
in small triangle
57 + 24 + z = 180 degree (sum of interior angles of a triangle )
81 + z = 180
z = 180 - 81
z = 99 degree
in big triangle
x + 43 + y = 180 degree (sum of interior angles of a triangle )
56 + 43 + y = 180
99 + y =180
y = 180 - 99
y = 81 degree
The value of x= 56°
Hope it helps you...



Dose anyone mind if they could help me on this problem that I'm stuck on? thank you so much if you do!

Answers
Answer:
V = π(6^2)(8) = 288π cu. in.
= 904.78 cu. in.
look at the rats people. look at em

Answers
these rats look so delicate and peaceful
Step-by-step explanation:
just like you could float in the air and dance with rats amazing.
write the system first as a vector equation and then as a matrix equation. 5x1 − x2 = 6 7x1 9x2 =
Answers
The vector equation is: x1 * (5, 7) + x2 * (-1, 9) = (6, )
- The matrix equation is: | 5 -1 | | x1 | = | 6 | and | 7 9 | | x2 | = | |
To write the given system first as a vector equation and then as a matrix equation, follow these steps:
1. Write the given system of equations:
5x1 - x2 = 6
7x1 + 9x2 =
2. Rewrite the system as a vector equation:
x1 * (5, 7) + x2 * (-1, 9) = (6, )
3. Write the matrix equation:
A * X = B
where A is the matrix of coefficients, X is the matrix of variables, and B is the matrix of constants.
4. Create matrix A using the coefficients of x1 and x2:
A = | 5 -1 |
| 7 9 |
5. Create matrix X using the variables x1 and x2:
X = | x1 |
| x2 |
6. Create matrix B using the constants of the system:
B = | 6 |
| |
So the matrix equation is:
| 5 -1 | | x1 | = | 6 |
| 7 9 | | x2 | = | |
To summarize:
- The vector equation is: x1 * (5, 7) + x2 * (-1, 9) = (6, )
- The matrix equation is: | 5 -1 | | x1 | = | 6 | and | 7 9 | | x2 | = | |
#SPJ11
ASAP PLZ
Aqua town charges $4.50 admission plus $0.75 for each ride. The cost at Wet World is $2.50 admission plus $1.25 per ride. Write an equation for the cost of going to Aqua Town. Write an equation for the cost of going to wet world. How many rides would you have to ride for both water parks to cost the same amount? What would the cost be? Write a system of equations( put your two equations equal to each other)to solve for x and y. Write your answer in the form (x,y).
Answers
Answer:
9.00
Step-by-step explanation:
X1,X2,...,XnX1,X2,...,Xn be a random sample of size n from the exponential distribution whose pdf isf(x:θ)=(1/θ)e−x/θ,0
Answers
To maximize the likelihood function, we take the derivative with respect to θ and set it equal to zero: d/dθ[L(θ|X1,X2,...,Xn)]=−n/θ+(X1+X2+⋯+Xn)/θ2=0.
The MLE for θ in the exponential distribution is simply the sample mean of the observed data.
The exponential distribution is a continuous probability distribution that describes the time between events in a Poisson point process. X1,X2,...,XnX1,X2,...,Xn is a random sample of size n from this distribution, which means that each XiXi is an independent and identically distributed random variable with the same exponential distribution.
The probability density function (pdf) of the exponential distribution is given by f(x:θ)=(1/θ)e−x/θ, where θ is the scale parameter. This means that the probability of observing a value x from the distribution is proportional to e−x/θ, with the constant of proportionality being 1/θ.
To estimate the value of θ based on the observed data, we can use the method of maximum likelihood estimation (MLE). The likelihood function for the sample X1,X2,...,XnX1,X2,...,Xn is given by L(θ|X1,X2,...,Xn)=∏i=1n(1/θ)e−Xi/θ=(1/θ)n e−(X1+X2+⋯+Xn)/θ.
Solving for θ, we get θ=(X1+X2+⋯+Xn)/n, which is the sample mean.
Know more about exponential distribution here:
https://brainly.com/question/31130457
#SPJ11
PPPPlease help meeee!

Answers
Answer:
A
Step-by-step explanation:
Since the theta is in second quadrant, x will be negative and y positive. cos(theta)=-2/sqrt(29)=B/H, the base is 2 and H=sqrt(29). The perpendicular is 5.
6 - 6x = 7x - 9x - 22
What is the value of x ?
Answers
Answer:
x=7
Step-by-step explanation:
Answer:
x = 7
Step-by-step explanation:
6 - 6x = 7x - 9x - 22
combine like terms
6 - 6x = -2x - 22
+2x +2x
6 -4x = -22
-6 -6
-4x = -28
divide both sides by -4
x = 7
Hope this Helps!!!
Which expression is equivalent to 4x2 - 4x – 3 in factored form?
Answers
Answer:
(2x-3)(2x+1)
Step-by-step explanation:
4x^2 - 4x - 3
we need two numbers that give 12 when multiplied and 4 when subtracted
the numbers are 6 and 2 because 6*2=12 and 6-4=4.
4x^2 - (6-2)x -3
4x^2 -6x +2x -3
take common
2x(2x -3)+1(2x-3)
take (2x-3) as common
(2x-3)(2x*1 + 1*1)
(2x-3)(2x+1)
When xb= 12, y = 8. Find x when y = 12
Answers
Answer:
If it is direct proportionality, then y = kx where k is a constant. Use the given information to find k:
8 = k(12) ⇒ k = 8/12 = 2/3
y = (2/3) x
For y = 12,
12 = (2/3) x ⇒ x = (3/2)*12 = 18
x = 18 when y = 12
I hope this helps a little bit.
Draw (daily) budget constraints with leisure on the x-axis and income on the y-axis (assuming the price of all-other-goods is $1) to illustrate the two proposals for a representative individual as well as the original budget constraint with no policy. Assume that an individual works, on average, 200 days per year so the $3000 income guarantee is equivalent to $15 per day. Also assume the wage rate is $5 per hour.
Answers
To illustrate the budget constraints, let's consider the two proposals for a representative individual and the original budget constraint with no policy.
Proposal 1: Income Guarantee of $3000 per year ($15 per day)
In this proposal, the individual receives an income guarantee of $3000 per year, which is equivalent to $15 per day. We can plot the budget constraint with leisure on the x-axis and income on the y-axis.
The slope of the budget constraint represents the wage rate, which is $5 per hour. Assuming an individual works an average of 200 days per year, the maximum income can be calculated as follows:
Max Income = Wage Rate * Hours per Day * Days per Year
= $5/hour * 8 hours/day * 200 days/year
= $8000
Therefore, the budget constraint with the income guarantee of $3000 per year would be a straight line passing through the point (0, $3000) and (160, $5000) since $5000 is the income level when all days are worked (200 days * $25 per day).
Proposal 2: Original Budget Constraint with No Policy
In this proposal, we consider the original budget constraint with no policy. Assuming the wage rate is $5 per hour and the individual works an average of 200 days per year, the maximum income is still $8000. The budget constraint without any policy would also be a straight line passing through the point (0, $0) and (160, $8000).
To illustrate both proposals and the original budget constraint on the same graph, we can plot the budget constraints as straight lines with leisure on the x-axis and income on the y-axis. The budget constraints would intersect at different points representing the different policies.
Note: Without specific information about the leisure-income trade-off or any additional policies, it is difficult to provide precise coordinates for the intersection points or the slopes of the budget constraints. The graph provided is a general representation to illustrate the concepts.
To know more about budget refer here
https://brainly.com/question/31952035#
#SPJ11
Earth makes a full rotation every
24 hours, Noptune makes a full rotation
every 16 hours. What is the ratio of
Earth rotations to Neptune Rotations?
(in simplest terms)
Answers
Answer:
I think the ratio is 3:2 :)
The radius of a bade if a cone is 8 cm. The height is 15 cm. What is the volume of the cone?
Answers
Answer: 1,004.8 or 320\(\pi\)
Step-by-step explanation:
\(\frac{1}{3} \pi 8^{2} 15=1,004.8\)
Dregg guessed the answers to three multiple-choice questions on a test. If each questions had 5 different choices, how many different answer combinations were there?
Answers
There were 10 different combinations to the multiple choice questions.
What is Combination?Combination is defined as “An arrangement of objects where the order in which the objects are selected does not matter.” The combination means “Selection of things”, where the order of things has no importance.
It is a way of selecting items from a collection where the order of selection does not matter. Suppose we have a set of three numbers P, Q and R. Then in how many ways we can select two numbers from each set, is defined by combination.
\(C_{n,r} = \frac{n!}{(n-r)! r!}\)
where n = 5
r = 3
\(C_{5,3} = \frac{5!}{(5-3)!3!} \\= \frac{5!}{2!3!}\)
= \(\frac{5(4)(3!)}{2!3!}\)
= 20/2
= 10 ways
Learn more about combinations here: https://brainly.com/question/11732255
#SPJ1