I need help with this math problem

Answer:

d=-6.5

Step-by-step explanation:

2d+13=0

2d=-13

d= -13/2

d=-6.5

Answer:

B.  -414,720 x⁷y⁶

Step-by-step explanation:

To find the 4th term of the expansion of (2x - 3y²)¹⁰, we can use the binomial theorem.

The binomial theorem states that for an expression of the form (a + b)ⁿ:

\(\displaystyle (a+b)^n=\binom{n}{0}a^{n-0}b^0+\binom{n}{1}a^{n-1}b^1+...+\binom{n}{r}a^{n-r}b^r+...+\binom{n}{n}a^{n-n}b^n\\\\\\\textsf{where }\displaystyle \rm \binom{n}{r} \: = \:^{n}C_{r} = \frac{n!}{r!(n-r)!}\)

For the expression (2x - 3y²)¹⁰:

Therefore, each term in the expression can be calculated using:

\(\displaystyle \boxed{\binom{n}{r}(2x)^{10-r}(-3y^2)^r}\quad \textsf{where $r = 0$ is the first term.}\)

The 4th term is when r = 3. Therefore:

\(\begin{aligned}\displaystyle &\;\;\;\;\:\binom{10}{3}(2x)^{10-3}(-3y^2)^3\\\\&=\frac{10!}{3!(10-3)!}(2x)^7(-3y^2)^3\\\\&=\frac{10!}{3!\:7!}\cdot2^7x^7(-3)^3y^6\\\\&=120\cdot 128x^7 \cdot (-27)y^6\\\\&=-414720\:x^7y^6\\\\ \end{aligned}\)

So the 4th term of the given expansion is:

\(\boxed{-414720\:x^7y^6}\)

The system of equations is.

\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)

And the solutions are y = 50 and x = 10.

Let's define the two variables:

With the given information we can write two equations, then the system will be:

\(\begin{cases}\text{x}+\text{y}=60 \\15\text{x}+10\text{y}=800 \end{cases}\)

Now let's solve it.

We can isolate x on the first  to get:

\(\text{x} = 60 - \text{y}\)

Replace that in the other equation to get:

\(15\times(60 - \text{y}) + 10\text{y} = 800\)

\(-2\bold{y} = 900 - 800\)

\(-2\bold{y} = 100\)

\(\text{y} = \dfrac{100}{-2} = \bold{50}\)

Then \(\bold{x=10}\).

Therefore, the solutions are y = 50 and x = 10.

Learn more about systems of equations at:

https://brainly.com/question/31812807

Answer:

A = 50x - 25

Step-by-step explanation:

The area (A) of the rectangle is calculated as

A = length × width

   = 4 \(\frac{1}{6}\) (12x - 6) ← change mixed number to improper fraction

  = \(\frac{25}{6}\) (12x - 6) ← multiply each term in the parenthesis by \(\frac{25}{6}\)

   = 50x - 25

A digit to make the number divisible by 3 is by adding the digit 2 to the number 1234.

To make the number 1234 divisible by 3, we can find the sum of its digits and determine if it is divisible by 3. If the sum of the digits is divisible by 3, then the original number is also divisible by 3.

Let's calculate the sum of the digits in 1234:

1 + 2 + 3 + 4 = 10

The sum of the digits is 10. Since 10 is not divisible by 3, we need to add or subtract a digit to make the sum divisible by 3.

To find the digit we need to add or subtract, we can use the fact that the difference between the original sum and the next multiple of 3 is the required digit.

The next multiple of 3 greater than 10 is 12 (12 - 10 = 2). Therefore, we need to add 2 to the number 1234 to make it divisible by 3.

1234 + 2 = 1236

we obtain the number 1236, which is divisible by 3.

For more such questions on divisible

https://brainly.com/question/29373718

#SPJ8

Answer: 1/4 s^2 or \(\frac{1}{4} s^{2}\)

Answer:

\(-9\sqrt{5} \) i believe

Step-by-step explanation:

For the given figure,   x = 23°  and      y = 129°

Parallel lines:

                        Parallel lines are lines that always stay the same distance apart and never meet.

Transversal line :

                             A transversal is a line that crosses two or more other lines.

given,

     ∠TLN = (3x - 18)°

    ∠MZQ = (5x + 14)°

    ∠NLM = y°

Now,

         ∠MZP + ∠MZQ = 180°  (Linear Pair)

        ∠MZP  = 180° - ∠MZQ  ...........(I)

again,

          ∠NLM + ∠TLN  =180°  ...........(II)      (Linear Pair)

  As,         ∠TLN = ∠MZP  (Corresponding Angle)

             (3x - 18)° =  180° - ∠MZQ  

           (3x - 18)° = 180° - (5x + 14)°

         3x + 5x  = 180° - 14° + 18°

           8x = 184°

           x = 184 / 8

          x = 23°

      From (II),

      ∠NLM + ∠TLN  =180°

    y° + 3x - 18° = 180°

 y = 180 - 3x + 18

     = 180 - 3* 23 + 18

      = 180 - 69 +18

     y = 129°

For the given figure,

                                     x = 23°  and      y = 129°

To learn more about Parallel line visit:

https://brainly.com/question/17432060

#SPJ9

If f is a one-to-one function and g is the inverse of f, then (f°g)(x) = x and (g°f)(x) = x.

We have,

(f°g)(x) means applying the function f to the result of applying the function g to x.

Since g is the inverse of f, applying f to the result of applying g to x will give us back x.

(g°f)(x) means applying the function g to the result of applying the function f to x.

Since g is the inverse of f, applying g to the result of applying f to x will also give us back x.

In both cases, the compositions result in the original input value x.

Thus,

If f is a one-to-one function and g is the inverse of f, then (f°g)(x) = x and (g°f)(x) = x.

Learn more about functions here:

https://brainly.com/question/28533782

#SPJ1

quotient of the expression 7a2b − b + 5.

power is "how many times you multiply a number or variable by itself.

given that ,the quantity 35 times a to the third power times b to the second power minus 5 times a to the second power times b plus 25 times a times b end quantity divided by the quantity 5 times a times b end quantity

The expression can be represent as follows:

\((35a^3b - 5ab^2 + 25ab) / (5ab)\)

take common 5ab in numerator part then ,

= \((5ab) * (7a^2b - b + 5) / (5ab)\)

after solving the equation,

= \(7a^2b - b + 5\)

Therefore, the quotient is \(7a^2b - b + 5\).

know more about quotient visit:

https://brainly.com/question/16134410

#SPJ1

Answer:

The answer is D

7a2b − a + 5

Step-by-step explanation:

7a2b − a + 5

Answer:

23/8

Step-by-step explanation:

9514 1404 393

Answer:

  (3/2π -(9/4)√3) m² ≈ 0.8 m²

Step-by-step explanation:

The area of the segment is the difference between the area of the sector and the area of the triangle.

  sector area = 1/2r²α . . . . where r is the radius and α is the central angle in radians

  triangle area = 1/2r²·sin(α) . . . . same variable definitions

Then the area of the segment is ...

  segment area = sector area - triangle area

  segment area = (1/2)r²(α -sin(α))

The central angle subtended by the segment is 360° -300° = 60° = π/3 radians

Then the segment area is ...

  A = (1/2)(3 m)²(π/3 -√3/2) = (3/2π -(9/4)√3) m² ≈ 0.8 m²

The orthogonal trajectories for the family of curves 3x^2 − y^2 = C are circles with the equation x^2 + y^2 = C/3.

To find this, we can take the derivative of the original equation 3x^2 − y^2 = C with respect to x, which will give us 6x. Then, we can take the negative reciprocal of this derivative, which is -1/6x. This is the slope of the orthogonal trajectories.

We then can use the point-slope form of a line to get y - y1 = -1/6x (x - x1). Since the slope of the orthogonal trajectories is always -1/6x, we can just set the equation y - y1 = -1/6x (x - x1) equal to 0 and solve for x to get x1 = -y1/6.

We can then plug this value back into the point-slope equation to get y - y1 = -1/6(-y1/6) (x - (-y1/6)), which simplifies to y - y1 = y1/6 + x. Now, if we let y1 = -C/3, then we get y - (-C/3) = C/6 + x, which can be rewritten as x^2 + y^2 = C/3.

Therefore, the orthogonal trajectories for the family of curves 3x^2 − y^2 = C are circles with the equation x^2 + y^2 = C/3.

Learn more about orthogonal trajectories here:

https://brainly.com/question/28164318

#SPJ4

Answer:

Down

Step-by-step explanation:

The "parent function" is  y = |x|, which opens up.

Changing the sign to y = -|x| flips (reflects) the graph over the x-axis, so the new graph opens down.  Adding 9 shifts the graph up 9 units, but that does not change the way the graph opens.

See the attached image.

y = |x| purple

y = -|x| black

y = -|x| + 9 red

The probability that the animal's weight will be less than 151 pounds is 0.50.

The correct option is B.

Since the given probability distribution ranges from 148 to 152, and we need to find the probability that the animal's weight will be less than 151 pounds, we can add the probabilities corresponding to the weights less than 151.

From the distribution, we see that the probability of the animal's weight being less than 151 pounds is 0.2 + 0.3 = 0.5.

Therefore, the answer is O 0.50.

Learn more about probability at: https://brainly.com/question/251701

#SPJ1

Answer:

520 Grams EASY

Step-by-step explanation:

Answer:

52,000

Step-by-step explanation:

You have to multiply the mass value by 1,000.

Answer:

it is 0 so that is x

Step-by-step explanation:

Answer:

the answer is 4800

Answer:

What is mental math?

Mental math is definitely what it sounds like—doing math in your head. But it’s also more nuanced than that. Being good at mental math tricks doesn’t mean that you’re able to solve 8974387 x 396 in your head instantly; while cool, that wouldn’t be very practical for daily life. So what does mental math mean?

It really just means being able to calculate in your head. It doesn’t mean you can solve every type of problem every time, nor is it a skill that you either “have” or “don’t have”; it’s a skill that you can learn, practice, and improve so that you can solve a bigger range of problems. And mental math certainly doesn’t have to be entirely in your head, either. Jotting down the numbers you need to remember to give you a head start (no pun intended), or writing down your solutions at each “step,” does not negate the “mental”-ness of the math.

Is mental math useful?

Ask this question again next time you’re trying to figure out a tip or doing any kind of construction or home improvement project! And, in addition to handy practical uses, knowing how to do mental math can also just keep your brain sharp and curb your reliance on calculators. Because, come on, doesn’t it feel good to reach for a calculator only to realize, “Wait, I don’t need it!” and figure out the answer in your head? (Spoiler: It does!) Not to mention knowing how to mentally solve small, simple math problems can save you some steps and help you out if you do need to solve a more complicated, difficult problem. There are always going to be some math problems that it would be silly to not solve with a calculator, but, yes, mental math is useful. And if you’re wondering if math itself is useful, math lessons you’ll actually use in real life.

Step-by-step explanation:

Given:

In triangle ABC, D is incenter m∠ACB = 3x + 54 and m∠ACD = x + 31.

To find:

m∠ACD.

Solution:

We know that,

Incenter of a triangle is the intersection point of all angle bisectors.

\(\angle ACD=\angle BCD\)      ...(i)

Now,

\(\angle ACB=\angle ACD+\angle BCD\)

\(\angle ACB=\angle ACD+\angle ACD\)       [Using (i)]

\(\angle ACB=2\angle ACD\)

Substitute the values, we get

\(3x+54=2(x+31)\)

\(3x+54=2x+62\)

\(3x-2x=62-54\)

\(x=8\)

The value of x is 8.

\(m\angle ACD=x+31\)

\(m\angle ACD=8+31\)

\(m\angle ACD=39\)

Therefore, the measure of angle ACD is 39 degrees.

Answer:

V = 1130.4 cm³

Step-by-step explanation:

Given that V varies jointly with r² and h then the equation relating them is

V = kr²h ← k is the constant of variation

To find k use the condition when r = 3 and h = 5 then V = 141.3 , then

141.3 = k × 3² × 5 = 45k ( divide both sides by 45 )

k = 3.14 ← note approximation for π

V = 3.14r²h ← equation of variation

When r = 6 and h = 10, then

V = 3.14 × 6² × 10 = 3.14 × 36 × 10 = 1130.4 cm³

Answer: 0.00923521

Step-by-step explanation:

Given : The probability U.S households play video or computer games=69%=0.69

here, the probability of each U.S household play video or computer games is fixed as 0.69

Then, the probability of each U.S household not play video or computer games= 1-0.69=0.31

For independent events the probability of their intersection is product of probability of each event.

Now, the probability that none play video/computer games will be :-

\((0.31)^4=0.00923521\)

The average rate of change of g(x) = 2^x - 1 between x = 3 and x = 7 is: 30.

To find the average rate of change of a function, use the formula below:

Average rate of change = g(b) - g(a) / b - a.

Given the following:

Therefore:

a = 3

g(a) = \(2^3 - 1\) = 8 - 1

g(a) = 7

b = 7

g(b) = \(2^7 - 1\) = 128 - 1

g(b) = 127

Substitute the values into the formula:

Average rate of change = (127 - 7) / 7 - 3

= 120/4

Average rate of change = 30

Learn more about the average rate of change on:

https://brainly.com/question/11627203

#SPJ1

Answer: the answer is 30, i took the test.

The function that models the relationship between the number of students enrolled, f(x) and the number of years after 2015, x,  is D. f(x) = 3000(0.98)*.

Mathematically, a function defines a mathematical relationship or an algebraic expression involving one variable (the independent variable) and another variable (the dependent variable).

There are four main types of mathematical functions, including:

The number of students enrolled in 2015 = 3,000

The annual decrease in students enrollment = 2%

Let f(x) the model modeling the relationship between the number of students enrolled and the number of years after 2015.

Let the number of years after 2015 = x.

Thus, the correction function is D. f(x) = 3000(0.98)*.

Learn more about mathematical functions at https://brainly.com/question/11624077.

#SPJ1

Answer:

The table represents a nonlinear function because the rate is not constant.

Step-by-step explanation:

As shown in the picture below, the x side of the table has the same rate of change of +1. However, due to the fact that the y side does not have the same rate of change, +6 and +3, the table represents a non linear function. If the rate on the y side of the table were all the same, then this would be a Linear function.

Answer:

\(61.8^{\circ}\)

Step-by-step explanation:

Vertical angles are congruent

Answer:

61.8

Step-by-step explanation:

The measure of angle C is 61.8 degrees.

Vertical angles are a pair of nonadjacent angles formed by two intersecting lines. They are called "vertical" because they are opposite each other and share the same vertex (the point at which the two lines intersect). Because vertical angles share the same vertex, they are always congruent, which means that they have the same measure.

In this case, angles C and E are a pair of vertical angles, so they are congruent. Since the measure of angle E is 61.8 degrees, the measure of angle C must also be 61.8 degrees. Therefore, the answer is 61.8 degrees.

Answer: D:(-1,4)

R:(-4,4)

Step-by-step explanation:

I hope that correct

Answer:

7. 14

15. 30

28. 56

32. 64

18 36

x 2x

1/2y. y

2x. 4x

x+3 2x+9

Step-by-step explanation:

each out is double the in

Answer:

386.75

Step-by-step explanation:

added in the picture

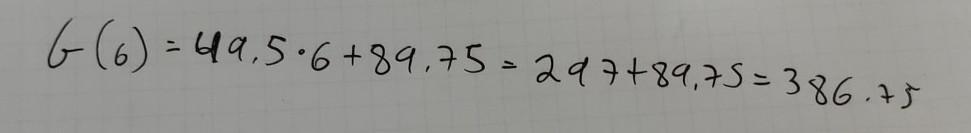
The cost of joining the gym for 6 months is 386.75.

Given,

The function G(m) = 49.5m + 89.75 represents the cost of joining the gym in addition to the one-time membership fee.

The cost, G, is measured in dollars for m months.

We need to find the value of G(6).​

Here,

The one-time membership = 89.75.

Now,

Putting m = 6 months in:

G(m) = 49.5m + 89.75

G(6) = 49.5 x 6 + 89.75

       = 297 + 89.75

       = 386.75

Thus the cost of joining the gym for 6 months is G(6) = 386.75.

Learn more about finding the value of a function here:

https://brainly.com/question/8822000

#SPJ2

Answer:

i. Only X and Y kill the bird = 2/5

ii. Only two of them kill the bird= 0.11

iii. Only Z kill the bird= 5/6

iv. Only one of them kill the bird= 1/3

v. None of them kill the bird= 0

vi. All of them kill the bird​= 1

Step-by-step explanation:

Probability of x= 3/5

Probability of y = 2/3

Probability of z = 5/6

i. Only X and Y kill the bird

= 3/5 * 2/3

= 2/5

ii. Only two of them kill the bird

=Either x and y or x and z or y and z

= 2/5 or 1/2 or 5/9

= 0.111

iii. Only Z kill the bird

= 5/6

iv. Only one of them kill the bird

= 3/5 or 2/3 or 5/6

= 1/3

v. None of them kill the bird

0

vi. All of them kill the bird​

1

Answer:

43/2

Step-by-step explanation:

Evaluate 12 - (3 y)/2 + y (2 y - 4/y) where y = 3:

12 - 3 y/2 + y (2 y - 4/y) = 12 - 3×3/2 + 3 (2×3 - 4/3)

Hint: | Express -3×3/2 as a single fraction.

-3×3/2 = (-3×3)/2:

12 + (-3×3)/2 + 3 (2×3 - 4/3)

Hint: | Multiply 2 and 3 together.

2×3 = 6:

12 - (3×3)/2 + 3 (6 - 4/3)

Hint: | Multiply -3 and 3 together.

-3×3 = -9:

12 + (-9)/2 + 3 (6 - 4/3)

Hint: | Put the fractions in 6 - 4/3 over a common denominator.

Put 6 - 4/3 over the common denominator 3. 6 - 4/3 = (3×6)/3 - 4/3:

12 - 9/2 + 3 (3×6)/3 - 4/3

Hint: | Multiply 3 and 6 together.

3×6 = 18:

12 - 9/2 + 3 (18/3 - 4/3)

Hint: | Subtract the fractions over a common denominator to a single fraction.

18/3 - 4/3 = (18 - 4)/3:

12 - 9/2 + 3 (18 - 4)/3

Hint: | Subtract 4 from 18.

| 1 | 8

- | | 4

| 1 | 4:

12 - 9/2 + 3×14/3

Hint: | Express 3×14/3 as a single fraction.

3×14/3 = (3×14)/3:

12 - 9/2 + (3×14)/3

Hint: | Cancel common terms in the numerator and denominator of (3×14)/3.

(3×14)/3 = 3/3×14 = 14:

12 - 9/2 + 14

Hint: | Put the fractions in 12 - 9/2 + 14 over a common denominator.

Put 12 - 9/2 + 14 over the common denominator 2. 12 - 9/2 + 14 = (2×12)/2 - 9/2 + (2×14)/2:

(2×12)/2 - 9/2 + (2×14)/2

Hint: | Multiply 2 and 12 together.

2×12 = 24:

24/2 - 9/2 + (2×14)/2

Hint: | Multiply 2 and 14 together.

2×14 = 28:

24/2 - 9/2 + 28/2

Hint: | Add the fractions over a common denominator to a single fraction.

24/2 - 9/2 + 28/2 = (24 - 9 + 28)/2:

(24 - 9 + 28)/2

Hint: | Evaluate 24 + 28 using long addition.

| 1 |  

| 2 | 8

+ | 2 | 4

| 5 | 2:

(52 - 9)/2

Hint: | Subtract 9 from 52.

| 4 | 12

| 5 | 2

- | | 9

| 4 | 3:

Answer: 43/2