Answers
The linear functions in this problem are given as follows:
2. y = -4x + 10.
3. y = -2/5x + 13/5.
4. y = 1/4x - 7/2
5. y = 3x + 20.
6. y = -2x + 3.
7. y = 4/3x + 2/3.
8. y = 1/3x - 6.
9. y = -3/2x + 8.
10. y = -1/5x + 43/5.
How to obtain the linear functions?The slope-intercept definition of a linear function is given as follows:
y = mx + b.
In which the parameters are listed as follows:
m is the slope.b is the y-intercept.In the context of this problem, the slope is obtained as follows:
If two lines are parallel, they have the same slope.If two lines are perpendicular, the multiplication of their slopes is of -1.Then the intercept is obtained replacing the x-coordinate and the y-coordinate of the point in the equation, and solving for b.
For example, in item 2, the slope of the line is of:
m = -4.
As the line is parallel to a line of slope -4.
Then:
y = -4x + b.
From the point, when x = 3, y = -2, then the intercept is obtained as follows:
-2 = -4(3) + b
b = -2 + 12
b = 10.
Hence the equation is of:
y = -4x + 10.
More can be learned about linear functions at https://brainly.com/question/24808124
#SPJ1
Related Questions
What is the volume of the following triangular prism?
252 yd
126 yd
42 yd

Answers
Answer:
V = 126 yd3
Step-by-step explanation:
The base: \(\frac{(9)(4)}{2} =\frac{36}{2} =18\)
The volume: \(v=(18)(7)=126yd^{3}\)
Hope this helps
Using the Pythagorean Theorem, find the distance between the points.

Answers
Answer:
(5,7,8.6)
Step-by-step explanation:
Create a line on each the x axis and the y axis which intersects at a right triangle. The x axis line is 7 squares and the y axis is 5 squares. Now you can use the Pythagorean theorem.
a^2+b^2=c^2
7^2+5^2=c^2
49+25=c^2
74=c^2
8.6=c
Which equation represents the function f(x) = (1.6)x after it has been translated 5 units up and 9 units to the right?
g(x) = (1.6)x + 5 − 9
g(x) = (1.6)x + 5 + 9
g(x) = (1.6)x − 9 + 5
g(x) = (1.6)x + 9 + 5
Answers
If the parent function \(\sf y=(1.6)^x\) is translated 5 units up and 9 units to the right, then you should subtract 9 from x and add 5 to the whole function. Thus,
1) translation the parent function \(\sf y=(1.6)^x\) 9 units to the right gives you the function \(\sf y=(1.6)^{x-9}\).
2) translation the function \(\sf y=(1.6)^{x-9}\) 5 units up gives you the function \(\sf y=(1.6)^{x-9}+5\)
Therefore, the correct choice is C
Learn more: brainly.com/question/11468584
to estimate the true mean speed of vehicles traveling on a particular section of roadway, a speed-detection device is programmed to measure the speed of the first 100 vehicles that pass it. are the conditions for constructing a t confidence interval met? no, the random condition is not met. no, the 10% condition is not met. no, the normal/large sample condition is not met. yes, the conditions for inference are met.
Answers
It's difficult to say whether the conditions for constructing a t-confidence interval are met based on the information provided. To construct a t-confidence interval, three conditions must be met:
The sampling method must be random. It's not specified in the problem whether the method of selecting the vehicles was random or not, so it's impossible to say whether this condition is met.
The sample size must be large enough. A sample size of 100 vehicles is considered to be large enough for the normal/large sample condition to be met.
The population must be approximately normally distributed or the sample size must be large. Since the problem does not specify anything about the distribution of the population, it is not clear if this condition is met.
Given that the information provided does not give enough details to state whether the conditions for constructing a t-confidence interval are met or not.
To learn more about percentages, refer to the link:brainly.com/question/13450942
#SPJ4
Suppose a company wants to introduce a new machine that will produce a marginal annual savings in dollars given by S '(x)= 175 - x^2, where x is the number of years of operation of the machine, while producing marginal annual costs in dollars of C'(x) = x^2 +11x. a. To maximize its net savings, for how many years should the company use this new machine? b. What are the net savings during the first year of use of the machine? c. What are the net savings over the period determined in part a?
Answers
a) To maximize its net savings, the company should use the new machine for 7 years. b) The net savings during the first year of use of the machine are $405 (rounded off to the nearest dollar). c) The net savings over the period determined in part a are $1,833.33 (rounded off to the nearest cent).
Step-by-step explanation: a) To determine for how many years should the company use the new machine to maximize its net savings, we need to find the value of x that maximizes the difference between the savings and the costs.To do this, we need to first calculate the net savings, N(x), which is given by:S'(x) - C'(x) = 175 - x² - (x² + 11x) = -2x² - 11x + 175To find the maximum value of N(x), we need to find the critical values, which are the values of x that make N'(x) = 0:N'(x) = -4x - 11 = 0 ⇒ x = -11/4The critical value x = -11/4 is not a valid solution because x represents the number of years of operation of the machine, which cannot be negative. (i.e., not use it at all).However, this answer does not make sense because the company would not introduce a new machine that it does not intend to use. Therefore, we need to examine the concavity of N(x) to see if there is a local maximum in the feasible interval.
To know more about maximizes visit:
https://brainly.com/question/30072001
#SPJ11
State the discriminant of 6x^2 - 2x + k, and state for which values of k would result in two different real solutions.
Please explain process.
Answers
The discriminant of the given equation 6x² - 2x + k as required is; 4 - 24k.
The value of k for which the equation will result in two different real solutions is; k < 1/6.
What is the discriminant of the given quadratic function?Since the discriminant for the standard form quadratic equation; y = ax² + bx +c is given by the formula;
Discriminant, D = b² - 4ac
On this note, since; a = 6, b = -2 and c = k.
Discriminant, D = (-2)² - (4 × 6 × k).
D = 4 - 24k
Recall, when discriminant, D > 0; the equation would result in two different real solutions.
Therefore; 4 - 24k > 0
-24k > -4
k < 1 / 6.
Read more on discriminant;
https://brainly.com/question/24308741
#SPJ1
help please? i made it to 10 points ill even put you as godly c:

Answers
Answer:
168...................
For each expression, write an equivalent expression that uses only addition.
20−9+8−7 = 11 + 1
4x−7y−5z+6 =
-3x−8y−4−87z
Answers
Equivalent expressions are expressions of equal values
The equivalent expressions are 4x+ (y - 8y) + (2z-5z) +6 and 6x-3x-6x + (2y - 10y) + (4 - 8) + (z - 88z)
How to determine the equivalent expressionsThe first expression has been solved.
So, we have the following expressions
4x−7y−5z+6 and -3x−8y−4−87z
4x−7y−5z+6
We have:
4x-7y-5z+6
Rewrite as:
4x+ (y - 8y) + (2z-5z) +6
-3x−8y−4−87z
We have:
-3x−8y−4−87z
Rewrite as:
3x-6x + (2y - 10y) + (4 - 8) + (z - 88z)
Hence, the equivalent expressions are 4x+ (y - 8y) + (2z-5z) +6 and 6x-3x-6x + (2y - 10y) + (4 - 8) + (z - 88z)
Read more about equivalent expressions at:
https://brainly.com/question/2972832
please help, will give brainlist to first answer

Answers
4.4300 grams
Answer:
3 .62 lt
4 4300 g
5 1.78 mt
6 .0031 g
7 500 lt
8 .083 g
Antonina needs to have worked at least 90 volunteer hours to graduate. She has already volunteered with a housing organization over the summer for 52 hours. Antonina needs to tutor after school for 3hours per week to complete the remainder of her volunteer hours. If www is the number of weeks that Antonina needs to tutor in order to complete her volunteer hours, which of the following inequalities best models the situation described above?
Answers
An inequality which best models the situation described above is: D. 52 + 3w ≥ 90.
What is an inequality?An inequality can be defined as a mathematical relation that compares two (2) or more integers and variables in an equation based on any of the following arguments (symbols):
Less than or equal to (≤).Less than (<).Greater than or equal to (≥).Greater than (>).In order to solve this word problem, we would assign a variable to the number of weeks and then translate the word problem into algebraic equation as follows:
Let w represent the number of weeks.
Translating the word problem into an algebraic equation, we have;
Volunteering hours = 52 hours.Remainder of her volunteer hours = 3w hours.Total time to graduate (at least) = 90 volunteer hours.Next, we would combine the above parameters to form an algebraic equation as follows:
52 + 3w ≥ 90
Read more on inequality here: brainly.com/question/6666926
#SPJ1
Complete Question:
Antonina needs to have worked at least 90 volunteer hours to graduate. She has already volunteered with a housing organization over the summer for 52 hours. Antonina needs to tutor after school for 3 hours per week to complete the remainder of her volunteer hours. If www is the number of weeks that Antonina needs to tutor in order to complete her volunteer hours, which of the following inequalities best models the situation described above?
answer choices
A. 52w + 30w ≥ 90
B. 52w + 30w ≤ 90
C. 52 + 3w ≤ 90
D. 52 + 3w ≥ 90
What is the forecast for May using a five-month moving average?(Round answer to the nearest whole number.) Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
A. 43 B. 47 C. 52 D. 38 E. 39
Answers
The forecast for May using a five-month moving average is 39 (Option E).
Moving average is used for smoothing out time series data to find any trends or cycles within the data. A five-month moving average is the average of the past five months. To calculate the moving average, add up the sales for the previous five months and divide it by five.
According to the question, the sales for the previous five months are: Nov. 39 Dec. 27 Jan. 40 Feb. 42 Mar. 41 April 47
We have to add the sales of these five months, which gives:
27 + 40 + 42 + 41 + 47 = 197
To find the moving average for May, we divide this sum by 5:
197 / 5 = 39.4
Since we have to round the answer to the nearest whole number, we round 39.4 to 39, which is option E.
Learn more about Moving average here: https://brainly.com/question/28495879
#SPJ11
what is an area of a square that has 3 inches as it's high and width? also would the answer be inches or inches squared?
Answers
Area of a square: side length ^2
Side lenght = 3 inches
Replacing:
A = 3 ^2 = 9 in2
Answer= 9 squared inches
the graph of a sinusoidal function has a maximum point at (0,5) and then has a minimum point at (2pi,-5). write the formula of the function, where x is entered in radians
Answers
The equation of the function is y = 10 * sin(x/2pi) + 5.
What is the sinusoidal function?
The period of a sinusoidal function is the time it takes for the sinusoidal function to complete one cycle of revolution.
The graph of a sinusoidal function can be represented by the equation:
y = A * sin(B(x - C)) + D
where A is the amplitude, B is the frequency, C is the horizontal shift, and D is the vertical shift.
From the information given, we know that the maximum point is at (0,5) and the minimum point is at (2pi,-5). We can use this information to find the values of A, B, C, and D.
The amplitude is the distance between the maximum and minimum points. In this case, it is 5 - (-5) = 10. So A = 10.
The period of the function is the distance between two consecutive maximum or minimum points. In this case, it is 2π.
So the frequency is 1/2π.
The horizontal shift is the amount by which the function is shifted along the x-axis. In this case, the maximum point is at x = 0, so the function is not shifted horizontally. So C = 0.
The vertical shift is the amount by which the function is shifted along the y-axis. In this case, the maximum point is at y = 5, so the function is shifted upward by 5. So D = 5.
So the equation of the function is:
y = 10 * sin(1/2pi (x - 0)) + 5
y = 10 * sin(x/2pi) + 5
where x is entered in radians.
Hence, the equation of the function is y = 10 * sin(x/2pi) + 5.
To learn more about the sinusoidal function visit,
https://brainly.com/question/30276869
#SPJ1
Last year, Ishiro Novato drove 21,986 miles and had these expenses: gas $1,187.25; maintenance and miscellaneous $118.80; parking and tolls $125.00; tires $300.00; wash and wax $75; insurance $614.80; license $34.90; and depreciation $1,780.00
Cost per Mile = Annual Variable Cost + Fixed Cost
Number of Miles Driven
it would mean a lot to me if someone would answer this for me
Answers
Answer:
$0.187 per mile
Step-by-step explanation:
The sum of the expenses for the year is ...
$1,187.25 +$118.80 +$300.00 +$75 +$614.80 +$34.90 +$1,780.00
= $4110.75
Then the cost per mile is ...
cost/miles = $4110.75 / 21986 ≈ $0.18697
The cost per mile is about $0.187, or 18.7¢ per mile.
__
If you need whole cents, that's about $0.19 per mile.
Question 21 of 31
What is the length of AC?
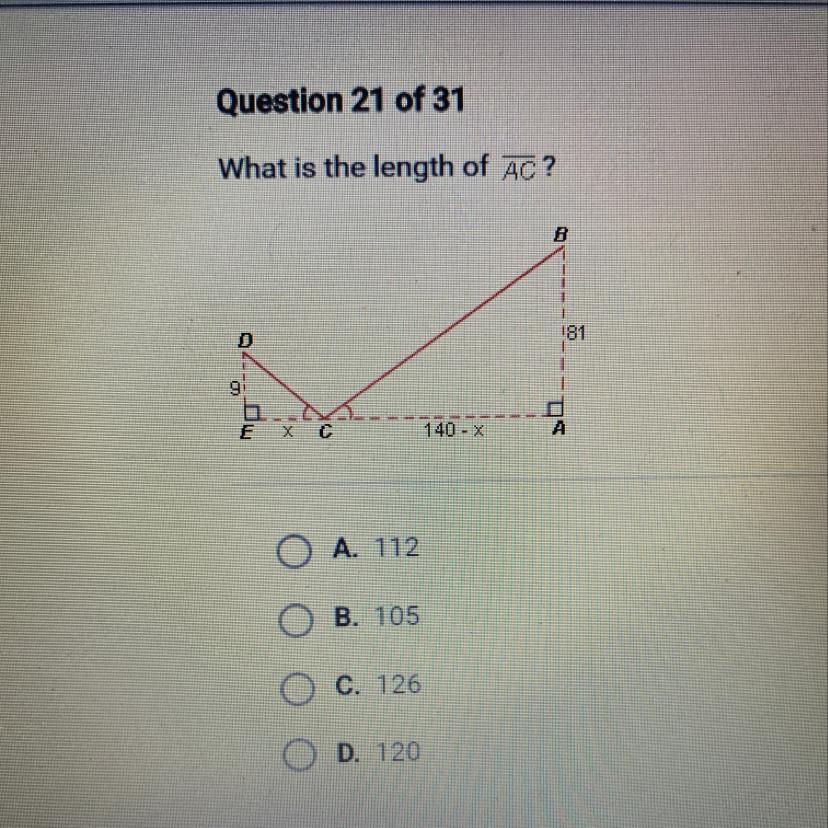
Answers
Answer:
C. 126
Step-by-step explanation:
We can use ratios to solve for corresponding side lengths.
\(\frac{140-x}{81} =\frac{x}{9}\)
Cross multiply.
\(9(140-x)=81x\)
\(140-x=9x\)
\(140=10x\)
\(14=x\)
Plug x as 14.
\(140-14=126\)
Walmart sells birthday cakes for. $18. After 3 days,they markdown the cakes by 45% . What is the discounted price after 3 days has passed?
Answers
he total cost for Larry, a mechanic for agricultural machines, can be expressed by the equafion \( T \mathrm{C}=50+10 Q^{2} \), whee \( Q \) is the number of repairs made by him. Which of the followin
Answers
The statements that are true for Larry's Auto Shop, with regards to the fixed cost and variable cost of the organization is the option A.
A. Statement I and II are true
What is a fixed cost?A fixed cost of production is a cost that remains the same as the production level changes. The basic infrastructure, rent, salaries, insurance, and taxes on the property are associated with the fixed cost of the organization.
The possible equation for the total cost for Larry, obtained from a similar question in the internet;
T = 50 + 10·q²
Where;
q = The quantities of repairs made by Larry's Auto Shop
I. When 0 repairs are produced, the variable cost is 0, therefore, the fixed cost = The total cost = 50 + 10 × 0² = 50
The fixed cost = The total cost
II. The above equation used to calculate the total cost = the fixed cost when 0 repairs are produced, indicates that the fixed cost = $50
III. The fixed cost is a fixed amount which remains the same for all amount of output produced, therefore, the the statement Larry Auto Shop's fixed cost depends on the level of output that is produced.
The possible statements in the question are;
I. When Larry's Auto Shop produces 0 repairs, its fixed cost equals its total cost
II. Larry's Auto Shop's fixed cost is equivalent to $50
III. The fixed cost of Larry Auto Shop depends on the level of output that is produced.
The options are;
(A) I and II are true
(B) I and III are true
(C) I, II, and III are true
(D) Statement I is true
Learn more on fixed and variable costs here: https://brainly.com/question/31523612
#SPJ4
Determine the number of classes in the frequency table below. Class Frequency 42-43 44-45 2 46-47 6 48-49 4 50-51 1 o 5 o 02 o 06 o 20
Answers
The number of classes in the frequency table as represented in the task content is; 5.
What is the number of classes in the frequency table?It follows from the task content that the number of classes in the frequency table as given in the task content is to be determined.
By observation, the data representation in the task content is a group data representation and hence, the classes are as follows;
42 - 4344 - 4546 - 4748 - 4950 - 51On this note, the number of classes in the frequency table as given in the task content is; 5.
Read more on classes in frequency table;
https://brainly.com/question/8470699
#SPJ1
Which equation gives the number of 1/4 centimetre that are in 7/8 centimetres
Answers
Answer:
2/8
Step-by-step explanation:
The skating rink charges 0.75 to rent skates and 1.25 per hour to take which equation can be used to find the number of hours (h) someone skated if he or she was charged 4.50
A) h(0.75+1.25)=4.50
B) 0.75+1.25=4.50
C) 0.75+1.25h=4.50
D) 0.75h+1.25=4.50
Answers
Answer: C
Step-by-step explanation:
ANSWER QUICK PLS
How many solutions does the equation have?
X - 5 + 3x = 4x - 9
- one
- two
- infinite
Answers
Answer:
Its 2
Step-by-step explanation:
two water taps together can fill a tank in 3 9 8 hours. the tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. find the time in which each tap can separately fill the tank
Answers
Answer:189 hours
Step-by-step explanation: 398 divided by 2 =199 -10 =189
CAN SOMEONE HELP ME OUT WITH THIS, PLEASE AND THANK YOU.

Answers
Answer:
5 7/20
Step-by-step explanation:
Yw
Answer:
\(5\frac{7}{20}\)
Step-by-step explanation:
First see if both mixed numbers have the same common denominators.
\(9\frac{1}{10} -3\frac{3}{4}\) different common denominators.
Find the LCM for both mixed numbers.
Answer: 20
10: 10, 20
4: 4, 8, 12, 16 and 20
Next convert each of the mixed numbers into a common denominator of 20.
\(9\frac{1}{10} =9\frac{2}{20}\) \(3 \frac{3}{4} = 3\frac{15}{20}\)
For \(9\frac{1}{10}\) multiply the denominator by 2 to get a common denominator of 20. Whatever number you multiplied to the denominator, you multiply it to the numerator. Except the whole number of course.
Same thing goes to the other fraction! I'm running out of time :(
Please help homework due

Answers
Answer:
X≤3
Step-by-step explanation:
This is because the arrow is moving down the number line
help me in this please

Answers
Answer:
35 rows and 35 numbers of plants in a row.
Step-by-step explanation:
Mark as brainliest
Find the volume of the solid generated by revolving the region bounded by the parabola y = x^2/4 and the line y = 1 about the following lines. a. The line y = 1 b. The line y = 2 c. The line y = -1 a. The volume of the given solid is . (Type an exact answer, using pi as needed.) b. The volume of the given solid is . (Type an exact answer, using pi as needed.) c. The volume of the given solid is . (Type an exact answer, using pi as needed.)
Answers
The volume of the solid generated by revolving the region bounded by the parabola y = x²/4 and the line y = 1 is 15π/4, and the line y = 2 is 37π/3 and the line y= -1 is 7π.
The parabola is y = x²/4 and the line is y = 1, y = 2 and y = -1 and it is needed to find the volume of the solid generated by revolving the region bounded by the parabola y = x²/4 and the line y = 1, 2 and -1 about these lines.
We sketch the parabola and the line y = 1. They intersect at points (-2, 1) and (2, 1). We rotate this shaded region about the line y = 1. So, the method of disks (washers) is appropriate here. We can integrate with respect to x, and so we slice perpendicular to the axis of rotation and integrate along x.
Axis of rotation: y = 1
Outer radius: R(x) = 1
Inner radius: r(x) = 1 - x²/4
Volume: V = π int_-2^2 (1² - (1 - x²/4)²)dx
On solving this, we get the volume of the solid generated by revolving the region bounded by the parabola y = x²/4 and the line y = 1 about the line y = 1 is V = 15π/4.
Now, we rotate this shaded region about the line y = 2. So, the method of disks (washers) is appropriate here. We can integrate with respect to x, and so we slice perpendicular to the axis of rotation and integrate along x.
Axis of rotation: y = 2
Outer radius: R(x) = 2 - x²/4
Inner radius: r(x) = 1
Volume: V = pi int_-2^2 ((2 - x²/4)² - 1²)dx
On solving this, we get the volume of the solid generated by revolving the region bounded by the parabola y = x²/4 and the line y = 1 about the line y = 2 is V = 37π/3.
Now, we rotate this shaded region about the line y = -1. So, the method of disks (washers) is appropriate here. We can integrate with respect to x, and so we slice perpendicular to the axis of rotation and integrate along x.
Axis of rotation: y = -1
Outer radius: R(x) = 1 + x²/4
Inner radius: r(x) = 1
Volume: V = pi int_-2^2 (1² - (1 + x²/4)²)dx
On solving this, we get the volume of the solid generated by revolving the region bounded by the parabola y = x²/4 and the line y = 1 about the line y = -1 is V = 7pi.
To learn more about parabola: https://brainly.com/question/4061870
#SPJ11
The figure below consists of a square and a right triangle. Find the missing length x.

Answers
Answer:
15 cm
Step-by-step explanation:
Since the square's side length is 8 cm, and one of its sides is the short leg of the triangle, the short leg of the triangle is 8 cm
Using the pythagorean theorem, solve for b (the missing side length x)
a² + b² = c²
8² + b² = 17²
64 + b² = 289
b² = 225
b = 15
So, the missing side length is 15 cm
Guide
A chemist mixes Chemical A and Chemical B to make a solution. She uses the same ratio of chemicals for each batch she
makes.
Drag numbers to complete the table.
?
4
6
12
Chemical A (ML) Chemical B (mL)
3
36
48
84
36
96
108
132
168
7
9
Answers
When chemist mixes Chemical A and Chemical B to make a solution
Part A
When the quantity of chemical B = 48 ml, then the quantity of chemical A = 4 ml
Part B
When the quantity of chemical A = 9 ml, then the quantity of chemical B = 108 ml
A chemist mixes Chemical A and Chemical B to make a solution
She uses the same ratio of chemicals for each batch
The solution A and B are in linear relationship
y = kx
Where y is the quantity of chemical A
x is the quantity of chemical B
k is the constant
Substitute the values in the table and find k
36 = k × 3
k = 36 /3
k = 12
Part A
When chemical B = 48 ml
48 = 12 × x
x = 48 / 12
x = 4 ml
Part B
When chemical A = 9 ml
y = 12 × 9
y = 108 ml
Therefore, when Chemical B = 48 ml, chemical B is 4ml . When chemical A = 9 ml, Chemical B = 108 ml
Learn more about ratio here
brainly.com/question/13637951
#SPJ4
Find the critical numbers of the function and describe the behavior of f at these numbers. (List your answers in increasing order.) f(x) = x10(x - 4)9 At ------------the function has ---Select--- a local maximum, a local minimum or not a max or a min. At ------------the function has ---Select--- a local maximum, a local minimum, or not a max or a min. At -------------the function has ---Select--- a local maximum a local minimum not a max or a min.
Answers
The critical numbers of the function f(x) = x¹⁰(x - 4)⁹are 0, 4. At x = 0, the function has a local minimum. At x = 4, the function has a local maximum.
Where does the function f(x) = x¹⁰(x - 4)⁹ have a local minimum and a local maximum?The function f(x) = x¹⁰(x - 4)⁹has critical numbers where its derivative equals zero or is undefined. To find these critical numbers, we need to take the derivative of the function. Applying the product and chain rules, we obtain the derivative f'(x) = 10x⁹(x - 4)⁹ + 9x¹⁰(x - 4)⁸.
To find the critical numbers, we set f'(x) equal to zero and solve for x. By factoring out common terms, we have 10x⁹ (x - 4)⁸(x + 9) = 0. This equation yields three solutions: x = 0, x = 4, and x = -9.
Next, we examine the behavior of f(x) at these critical numbers. At x = 0, the function has a local minimum. As x approaches 0 from the left, f(x) decreases. As x approaches 0 from the right, f(x) increases. Thus, at x = 0, the function reaches a minimum point.
At x = 4, the function has a local maximum. As x approaches 4 from the left, f(x) increases. As x approaches 4 from the right, f(x) decreases. Therefore, at x = 4, the function reaches a maximum point.
The critical number x = -9 is not included in the given intervals, so we do not consider it further.
Learn more about: Critical numbers
brainly.com/question/31339061
#SPJ11
The sum of three consecutive numbers is eighty-four. Create the equation you would use to solve this problem using x as the variable for the first of the three consecutive numbers. (Do not use spaces)
Answers
Answer:n= 27
Sorry solved for 48 instead of 8 first time around.
Step-by-step explanation:
