Answers
Both models give the elevation (in feet avobe sea leve) in function of the time.
In Bethanie's model; after 8 minutes (t=8) the elevation is 0 ft
In Mike's model; after 8 minutes the elevation is 210 ft
\(\begin{gathered} M(t)=t^3-6t^2+11t-6 \\ \\ M(8)=8^3-6(8^2)+11(8)-6 \\ M(8)=512-384+88-6 \\ M(8)=210 \end{gathered}\)Then, the person who drives to the higher elevation is MikeAnswer: C. Mike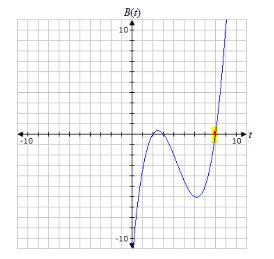
Related Questions
As an introduction to probability, a student is asked to roll a fair, six-sided number cube seven times. The results of those seven rolls are shown below.
1, 4, 4, 4, 4, 6, 5
What is the standard deviation of the data?
1.41
1.53
2.33
5
Answers
Answer:
B: 1.53
Step-by-step explanation:
The mean, or average, is 4, and n, the amount of numbers, is 7. To find the standard deviation, first, all of the numbers are subtracted by the mean. This makes (-3, 0, 0, 0, 0, 1, 2). Square all of them to get (9, 0, 0, 0, 0, 1, 4). Next add the squared numbers together (9 + 0 + 0 + 0 + 0 + 1 + 4 = 14). Next, the variance needs to be found. That is found by this formula: (Sum of previous number set ÷ (n - 1)). So in this case, (14 ÷ (n - 1)). Since n is 7, it is (14 ÷ (7 - 1)), or (14 ÷ 6). The answer to that is 2.3 repeating. After the variance is found, it is square rooted to get the standard deviation. √2.3 is about 1.53. Hope this helps! Have a great day! :)
4x + 9y =36 Convert the standard form to slope intercept form (y= mx+b)
Answers
y = (-4/9)x + 4
Answer:
4x+9y-36=0
Step-by-step explanation:
Use the slope-intercept form
y
=
m
x
+
b
to find the slope
m
and y-intercept
b
.
Slope:
−
4
9
y-intercept:
(
0
,
4
)
To evaluate whether customers enjoy the barista’s new smoothie, a restaurant manager surveys every other customer who orders the new smoothie. The manager determines that customers enjoy the new smoothie. Select all the statements that are true about the sampling method.
Answers
The sampling method used by the restaurant manager allows for efficient data collection and a representative sample, it may introduce bias and lacks randomization.
Based on the information provided, we can identify the following statements that are true about the sampling method used by the restaurant manager to evaluate customer satisfaction with the new smoothie:
1. The manager uses systematic sampling: The manager surveys every other customer who orders the new smoothie. This systematic approach involves selecting every second customer, providing a consistent and organized sampling method.
2. The sample is representative: By surveying every other customer who orders the new smoothie, the manager ensures that the sample includes a variety of customers, reflecting the customer population as a whole.
3. The sample size may be smaller than the total customer base: Since the manager surveys every other customer, the sample size may be smaller compared to surveying every customer. This allows for efficient data collection and analysis.
4.The sampling method may introduce bias: The manager may inadvertently introduce bias by only surveying every other customer. Customers who are skipped in the survey may have different preferences or opinions, leading to a potential bias in the results.
5. The sampling method lacks randomization: Randomization is not employed in this sampling method, as the manager systematically selects customers. This could potentially introduce bias or exclude certain types of customers from the sample.
for more such questions on sampling method
https://brainly.com/question/13219833
#SPJ8
A survey of 400 students yielded the following information: 262 were seniors, 215 were commuters, and 150 of the seniors were commuters. How many of the 400 surveyed students were seniors or were commuters?
Answers
Out of the 400 surveyed students, 327 were either seniors or commuters.
To find the number of students who were either seniors or commuters out of the 400 surveyed students, we need to add the number of seniors and the number of commuters while avoiding double-counting those who fall into both categories.
According to the information given:
There were 262 seniors.
There were 215 commuters.
150 of the seniors were also commuters.
To avoid double-counting, we need to subtract the number of seniors who were also commuters from the total count of seniors and commuters.
Seniors or commuters = Total seniors + Total commuters - Seniors who are also commuters
= 262 + 215 - 150
= 327
Therefore, out of the 400 surveyed students, 327 were either seniors or commuters.
It's important to note that in this calculation, we accounted for the overlap between seniors and commuters (150 students who were both seniors and commuters) to avoid counting them twice.
This ensures an accurate count of the students who fall into either category.
For similar question on surveyed.
https://brainly.com/question/14610641
#SPJ8
The mean diameter of holes produced by a drilling machine bit is 4.05 mm and the stan dard deviation of the diameters is 0.0028 mm For twenty holes drilled using this machine, determine, correct to the nearest whole num ber, how many are likely to have diame ters of between (a) 4.048 and 4.0553 mm and (b) 4.052 and 4.056 mm, assuming the diameters are normally distributed.
Answers
The total number of holes will be (a)15 and (b) 4 when the drilling machine is used whose standard deviation is 0.0028mm.
The square root of the variance is used to calculate the standard deviation, a statistic that expresses how widely distributed a dataset is in relation to its mean.
The sum of all values divided by the total number of values constitutes a dataset's mean.
The mean of the holes are given as 4.05 mm(\(\mu=4.08\))
The standard deviation is given as 0.0028 mm(\(\rho=0.0028\))
Now we will use the z-score and probability distribution to calculate the frequency of the holes to have diameter between 4.048 and 4.0553.
Here \(Pr(4.048\leq X\leq 4.0053)\) ,so we need to compute the z-values
\(Z_1=\frac{X_1-\mu}{\rho} \\Z_1=\frac{4.048-4.05}{0.0028} \\Z_1=-0.7143\)
Similarly:
\(Z_2=1.8929\)
Therefore from the above statements we can say that
\(Pr(-0.7143\leq X\leq 1.8929)\)
Solving for probability distribution we get
\(Pr(4.048\leq X\leq 4.0053)=0.7333\)
Total number of holes=0.7333 × 20= 14.666..
Therefore the number of holes is 15
Similarly
The z-value corresponding to 4.052 mm is given by 0.71
The z-value corresponding to 4.056 mm is given by:2.14
The probability of the diameter being between 4.052 mm and 4.056 mm is 0.4838 – 0.2611 =0.2227
The number likely to have a diameter between 4.052 mm and 4.056 mm = 0.2227 × 20
= 4.454
= 4, correct to nearest whole number
To learn more about standard deviation:
https://brainly.com/question/24298037
#SPJ9
A bird of species? A, when? diving, can travel six times as fast as a bird of species B top speed. If the total speeds for these two birds is 224 miles per hour
Answers
Answer:
Maximum speed of bird A is \(192\,\,\frac{mi}{h}\)
Maximum speed of bird B is \(32\,\,\frac{mi}{h}\)
Step-by-step explanation:
This is a problem with two unknowns: Max speed of bird A (we name that "A"), and max speed of bird B (we call that "B"). Now we can create two equations with these two unknowns, based on the info provided:
Equation 1): based on the phrase "bird A can travel six times as fast as bird B" we write:
\(A=6\,*\, B\\A=6B\)
Equation 2): based on the phrase; "the total speeds for these two birds is 224 miles per hour", we write:
\(A+B=224\,\,\frac{mi}{h}\)
Now, we use the first equation to substitute A in the second equation, ad then solve for the unknown B:
\(A+B=224\,\,\frac{mi}{h}\\(6B)+B=224\,\,\frac{mi}{h}\\7B=224\,\,\frac{mi}{h}\\B=\frac{224}{7} \,\,\frac{mi}{h}\\B=32\,\,\frac{mi}{h}\)
Now we can solve for the other unknown "A" using the substitution equation and the value of B we just found:
\(A=6B\\A=6\,(32\,\,\frac{mi}{h})\\A=192\,\,\frac{mi}{h}\)
Can you solve this problem so that you can explain me as best as possible to understand the problem?
It is called Combined Operations with fractions and I know that some will get the name confused but I think it is the same
Answers
Answer:
Answer: 2
Step-by-step explanation:
\( \frac{2}{3} (4 \frac{1}{6} - \frac{7}{6} ) \\ \)
express the mixed fraction into proper fraction:
\( { \boxed{4 \frac{1}{6} = \frac{(6 \times 4) + 1}{6} = \frac{25}{6} }}\)
then solve simplify:
\( = \frac{2}{3} ( \frac{25}{6} - \frac{7}{6} ) \\ \)
solve the bracket:
\( = \frac{2}{3} ( \frac{25 - 7}{6} ) \\ \\ = \frac{2}{3} ( 3)\)
then simplify:
\( = \frac{2 \times 3}{3} \\ \\ = 2\)
\(16 \: 3 \: by \: 4\)
evaluate the answer according to the law of exponents
Answers
Answer:
16 3/4=[16×4+3]/4=67/4 is your answer
Select the correct answer.
Which graph represents the solutions to this equation?
x2 + 8x = -20
(as a graph pls!)
Answers
Answer:
Step-by-step explanation:
Fill in the blank with the correct answer choice. A ___________ has exactly one pair of parallel lines. a. square c. trapezoid b. parallelogram d. rectangle Please select the best answer from the choices provided A B C D
Answers
Answer: C
Step-by-step explanation:
The rest of the quadrilaterals provided have 2 pairs of parallel lines.
The choice is:
CExplanation:
The quadrilateral that has exactly one pair of parallel lines is called a trapezoid.
Here's what a trapezoid looks like :
\(\setlength{\unitlength}{1 cm}\begin{picture}(0,0)\linethickness{0.3mm}\qbezier(0,0)(0,0)(1,3)\qbezier(5,0)(5,0)(4,3)\qbezier(1,3)(1,3)(4,3)\qbezier(3,0)(8.2,0)(0,0)\put(-0.5,-0.3){$\sf A$}\put(5.3,-0.3){$\sf B$}\put(4.2,3.1){$\sf C$}\put(0.6,3.1){$\sf D$}\end{picture}\)
Hence, this makes C the correct choice.Which inequality is represented by this graph?
Answers
Answer:
D) \(y> -\frac{1}{6} x +1\)
Step-by-step explanation:
It's going up so it has to be greater than sign, and it's dotted
Find the Value of Y.
Answers
The value of y in the triangle is 2√10 units.
How to find the side of similar triangle?Two triangles are said to be similar if their corresponding angles are congruent and the corresponding sides are in proportion .
The value of y can be found using the similar triangle ratios as follows:
Hence,
8 / y = y / 5
cross multiply
y² = 8 × 5
y²= 40
square root both sides of the equation
y = √40
Therefore,
y = 2√10 units
learn more on triangle here: https://brainly.com/question/22137601
#SPJ1
F(x) = 3x + 2
What is f(5)
Answers
Step-by-step explanation:
to find f(5) in f(x) , just put in '5' where 'x' is in the equation
f(5) = 3 (5) + 2 = 17
Answer:
f(5) = 17
Step-by-step explanation:
Let's evaluate the function for f(5)
\(\rm{f(x)=3x+2}\)Insert 5 everywhere x appears:
\(\rm{f(5)=3(5)+2}\)\(\rm{f(5)=15+2}\)\(\rm{f(5)=17}\)Therefore f(5) = 17
One lap around the track at Kathleen’s school is 0.4 kilometer. If Kathleen ran 3.5 laps, how many kilometers did she run?
Answers
Answer:
Kathleen ran 2 3/16miles
Answer:
The correct answer is option B
John wishes to choose a combination of two types of cereals for breakfast - Cereal A and Cereal B. A small box (one serving) of Cereal A costs $0.50 and contains 10 units of vitamins, 5 units of minerals, and 15 calories. A small box (one serving) of Cereal B costs $0.40 and contains 5 units of vitamins, 10 units of minerals, and 15 calories. John wants to buy enough boxes to have at least 500 units of vitamins, 600 units of minerals, and 1200 calories. How many boxes of each cereal should he buy to minimize his cost?
Answers
Let's assume that John buys x boxes of Cereal A and y boxes of Cereal B. Then, we can write the following system of inequalities based on the nutrient and calorie requirements:
10x + 5y ≥ 500 (minimum 500 units of vitamins)
5x + 10y ≥ 600 (minimum 600 units of minerals)
15x + 15y ≥ 1200 (minimum 1200 calories)
We want to minimize the cost, which is given by:
0.5x + 0.4y
This is a linear programming problem, which we can solve using a graphical method. First, we can rewrite the inequalities as equations:
10x + 5y = 500
5x + 10y = 600
15x + 15y = 1200
Then, we can plot these lines on a graph and shade the feasible region (i.e., the region that satisfies all three inequalities). The feasible region is the area below the lines and to the right of the y-axis.
Next, we can calculate the value of the cost function at each corner point of the feasible region:
Corner point A: (20, 40) -> Cost = 20
Corner point B: (40, 25) -> Cost = 25
Corner point C: (60, 0) -> Cost = 30
Therefore, the minimum cost is $20, which occurs when John buys 20 boxes of Cereal A and 40 boxes of Cereal B.
Fizzy Waters promotes their alkaline water product for everyone on the basis that alkaline water is good for health as it neutralizes acids produced in the body. They boast having a mean alkalinity level of 50 mg/liter. Alkaline water has a higher pH level than regular drinking water and Fizzy Waters claims that its higher Hydrogen content provides better hydration than regular water. To test their claim, you contact Fizzy Waters and they allow you to collect samples from their manufacturing plant to test for yourself. You collect 100 random samples of their alkaline water and find that the mean and standard deviation are y = 32.2mg/liter and 14.4mg/liter. With 99% confidence, is there enough evidence to support their claim that the population mean exceeds 50 mg/liter?
Answers
Answer:
The mean of 50 mg/liter is not inside the 99% interval, so there is not enough evidence to support their claim.
Step-by-step explanation:
First we need to find the z-value for a confidence of 99%
The value of alpha for a 99% confidence is:
\(1-\alpha/2 = 0.99\)
\(\alpha/2 = 0.01\)
\(\alpha = 0.005\)
Looking in the z-table, we have z = 2.575.
Now we can find the standard error of the mean:
\(\sigma_{\bar{x} }= s_x/\sqrt{n}\)
\(\sigma_{\bar{x} }= 14.4/\sqrt{100}\)
\(\sigma_{\bar{x} }=1.44\)
Finding the 99% confidence interval, we have:
\(99\%\ interval = (\bar{x} - z\sigma_{\bar{x}}, \bar{x} + z\sigma_{\bar{x}})\)
\(99\%\ interval = (32.2 - 2.575*1.44, 32.2 + 2.575*1.44)\)
\(99\%\ interval = (28.492, 35.908)\)
The mean of 50 mg/liter is not inside the 99% interval, so there is not enough evidence to support their claim.
Wich expression is equivalent to 3 ^ 4 x 3 ^ -9
Answers
Answer:
Step-by-step explanation:
3^4 · 3^-9 = 3^4 · 1/3^9
Hope it helped!
The circumference of a circle is 119.32 in what is the diameter of the circle?
Answers
Answer:
38
Step-by-step explanation:
119.32/3.14 since 3.14 is pi and c=pi*d
Answer:
d≈37.98
Step-by-step explanation:
C=2πr
d=2r
Solving for d
d=C
π=119.32
π≈37.98074
Solve the two simultaneous equations.
You must show all your working.
3t+2p=15.5
5t+4p=28.5
Answers
Answer:
Given equations are,
5x+2y=−2 (1)
3x−5y=17.4 (2)
Multiply equation (1) by 5 and equation (2) by 2, we get,
5(5x+2y)=5×−2
∴25x+10y=−10 (3)
2(3x−5y)=2×17.4
∴6x−10y=34.8 (4)
Adding equations (3) and (4), we get,
31x=24.8
∴x=
31
24.8
Put this value in equation (1), we get,
5(
31
24.8
)+2y=−2
∴
31
124
+2y=−2
∴2y=−2−
31
124
∴2y=
31
−186
∴y=
31
−93
Step-by-step explanation:
2 qt 1 c = __ fl oz
Answers
Please help me i need help.
Answers
Answer:
5x+7 > 17 matches with 3.
1+3x > -5 matches with 2.
2x+1 < 3 matches with 1.
5-3x > 11 matches with 4.
Step-by-step explanation:
identify the property being demonstrated
if x/5 = 7, then x=35
a. division
b. multiplication
c. reflexive
d. symmetric
Answers
Answer:
\( \: \: \: \: \: \: \: \: \: \: \dfrac{x}{5} = 7 \\ \implies \: x = 7 \times 5 \\ \implies \: x = 35\)
So,b. multiplication
Answer:
A. division
Step-by-step explanation:
\(x/5=7\)
\(x\) is being divided by an integer.
\(x=35\)
\(35/5=7\)
35 divided by 5 is equal to 7.
26
11°
X
130
(Round the answer to the nearest hundredth.)
The length of side x is
15319
Gaveart
067295
Answers
The length of side x is approximately 24.87, rounded to the nearest hundredth.
how can we find side of the triangle?
To find the length of side x, we can use the sine function, which relates the opposite side to an angle to the hypotenuse:
sin(11°) = opposite side/hypotenuse
Rearranging this equation, we get:
opposite side = sin(11°) * hypotenuse
We know that the hypotenuse has a length of 130, so we can substitute that in:
opposite = sin(11°) * 130
Using a calculator, we can evaluate sin(11°) to be approximately 0.1919, so we can substitute that in as well:
opposite = 0.1919 * 130
Simplifying this expression, we get:
opposite ≈ 24.87
Therefore, the length of side x is approximately 24.87, rounded to the nearest hundredth.
To know more about hypotenuse:
https://brainly.com/question/12006293
#SPJ1
Jakob used the table shown to find a ratio which is equivalent to 5:9
Answers
Answer:
theres nothing shown :(
For every 125 light bulbs a certain factory makes,2 are defective.At that rate,how many light bulbs out of 1000 light bulbs will be defective?
Explain your answer
Answers
2x500= 100
125x1000= 62500
Answer: 62500
The graph compares the weights in pounds of 100 dogs and cats that are brought in
to a veterinarian's office. Using the medians, how much more does a typical dog weigh than a typical cat?
Answers
Answer:20
Step-by-step explanation:this is wrong
Answer:
40
Step-by-step explanation:
subtract median of dogs and median of cats
HELP PLS ASAP!! ILL GIVE 10 BRAINLEST THINGYS !!!
Explain how to find the slope of the function without using technology.
2x + 3y = 12
Answers
Answer: The slope is −2/3
Step-by-step explanation:
2 x + 3 y = 12 is the standard form for a linear equation. To determine the slope, solve the equation for y in order to convert to the slope-intercept form y = m x + b , where m is the slope and b is the y-intercept.
2 x + 3 y = 12
Subtract 2 x from both sides.
3 y = − 2 x + 12
Divide both sides by
3 . y = − 2 /3 x + 12 /3 =
y = − 2 /3 x + 4
The slope is
− 2 /3
The construction engineer calculated that he needed 2 support pillars of equal size. He ordered 8 1/2 tons of concrete to make the support pillars. How much concrete did he use for each support pillar?
Answers
Step-by-step explanation:
If the engineer ordered 8 1/2 tons of concrete to make 2 support pillars of equal size, we can divide the total amount of concrete by 2 to find out how much concrete he used for each support pillar.
First, we need to convert the mixed number 8 1/2 to an improper fraction:
8 1/2 = 17/2
Now we can divide 17/2 by 2:
(17/2) ÷ 2 = (17/2) × (1/2) = 17/4
Therefore, the engineer used 17/4 tons of concrete for each support pillar.
Help pls!!!!!!!!!!!!!!!!!
Answers
Answer:
the answer is 8/5
Step-by-step explanation:
LCM = 10
(14+2)/10 = 16/10
= 8/5
please give me brainlist if it is helpful for you
At the U.S. Open Ternis Championship a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player was 97 miles per hour (mph) and the standard deviation of the serve speeds was 13 mph. Assume that the statistician also gave us the information that the distribution of the serve speeds was mound-shaped and symmetric. What proportion of the player's serves was between 110 mph and 136 mph
Answers
Step-by-step explanation:
At the U.S. Open Tennis Championship, a statistician keeps track of every serve that a player hits during the tournament. The statistician reported that the mean serve speed of a particular player was 102 miles per hour (mph) and the standard deviation of the serve speeds was 15 mph.