I NEED HELP PLEASE ASAP! :)
Anne is pushing a wheelbarrow filled with mulch to place in her garden. She is pushing the wheelbarrow with a force of 70 N at an angle of 50° with the horizontal. How much work in joules is Anne doing when she pushes the wheelbarrow 25 meters? (Show work)
Answers
Answer:
See below.
Step-by-step explanation:
Again, another great question!
This should be under physics, as it involves Work = Force * Distance. As Anne pushes the wheelbarrow with a force of 70 Newtons with respect to an angle of 50 degrees horizontal, the horizontal force is 70( cos 50 ). The distance over which the work is done is 25 meters, so work should be -
Work = ( 70( cos 50 ) )( 25 ),
Work = ( About ) 1124.87 Joules
The work done when Anne pushes the wheelbarrow a distance of 25 meters, is 1124.87 Joules
Related Questions
What the meaning of "Define F(x) = α if α is isomorphic to the initial segment of W given by x"?

Answers
The given statement defines a function F(x) that associates a unique ordinal number α to each initial segment of a well-ordered set W. The function F(x) assigns the ordinal α to the initial segment of W determined by x if and only if α is isomorphic (structurally equivalent) to that initial segment.
To prove the uniqueness of the ordinal number associated with each initial segment, we rely on Lemma 2.7 (presumably mentioned earlier). This lemma likely establishes some properties of isomorphic well-ordered sets, such as uniqueness of isomorphisms or a specific correspondence between ordinals and well-ordered sets.
Using the Replacement Axioms, we can show that the set F(W) exists, as it is obtained by applying the function F to each element of W and collecting the results as a set.
For each initial segment of W, there exists an ordinal α that is isomorphic to that segment; otherwise, we can consider the least element r for which no such ordinal exists. By definition, F(r) does not have a well-defined value, contradicting the construction of F.
Finally, if y is the least element in the set F(W), then F(W) = y, and we have established an isomorphism between W and the ordinal y.
In summary, the proof demonstrates that for any well-ordered set W, there exists a unique ordinal number (denoted by F(W)) that is isomorphic to W, confirming the statement that every well-ordered set is isomorphic to a unique ordinal number.
For more such questions on ordinal number
https://brainly.com/question/30954769
#SPJ8
Lines MN and GH are parallel. If the measure of angle 6 is 45°, what is measure of angle 4?

Answers
Answer: It will be A that is the best answers
Use the given function values and the trigonometric identities to find the exact value of each indicated trigonometric function.


Answers
Given :
The trigonometric functions are given
\(\sin 60^{\circ}=\frac{\sqrt[]{3}}{2},\cos 60^{\circ}=\frac{1}{2}\)To find :
The value of sin 30 degree.
Work out the area of a circle with radius of 7.5cm

Answers
Answer:
Area of circle is equal A = πr²
Here r = 7.5 and π = 3.142
so,
A = 3.142(7.5)²
A = 176.17 after rounding off.
6.
Circumference is the same as the area of a circle.
a. True
b. False
Answers
Answer:
TRUE
Step-by-step explanation:
i just know it :>
what is the diffrence between 48 degrees Fahrenheit and -13 degrees fahrenheit
Answers
Answer:
61
Step-by-step explanation:
=48 - -13
= 48 + 13
=61
Simplify fully 56:16
Answers
Answer:
7/2
Step-by-step explanation:
PLEASE HELP!!!
Please help me answer the questions that are circled, I really need help!

Answers
Answer:
Here:
Step-by-step explanation:
23. f(x) = \(\sqrt{x}\) and g(x) = \(x^2-5x\)
24. f(x) = \(x^2\) and g(x) = \(x^3+1\)
28. f(x) = \(e^x\) and g(x) = \(sinx\)
29. f(x) = \(cosx\) and g(x) = \(\sqrt{x}\)
Basically, you try to find a function contained inside a function if that makes sense. For example in question 23, g(x) itself is a function = \(x^2-5x\). Same with f(x) = \(\sqrt{x}\) . In this case, when we try to fo f(g(x)), we are basically replacing x in the f(x) function by the equation in g(x). Hope this makes sense.
if 5x/2 = -10 then the value of x is
Answers
Answer:
x= -4
Step-by-step explanation:
5x/2= -10
×2 ×2
5x = -20
/5 /5
x = -4
Answer:
x=-4
Step-by-step explanation:
5x/5=-10/1 then we do cross multiplication which = to 5x/5= -20/5 so x=-4
A cube has a volume of 1000cm^3. Work out the surface area Of the cube.
Answers
Answer:
600
Step-by-step explanation:
V = s×s×s = s³
V = 10×10×10 =1,000
Surface area
6a² = 6(10²) =600
If a math student Square both legs of a right triangle and the results were 441 and 400, what is the length of the hypotenuse of a triangle?
Answers
Answer:
\(29 \\ \)
Solution:
According to the Pythagorean Theorem, is that the square of the hypotenuse is equal to the sums of squares of the two legs in which if you take the square root of the sum you are going to get the actual length of the hypotenuse but the two legs are already squared so all you have to do now is sum them and take the square root of it.
\( \sqrt{441 + 400} \\ \sqrt{841} \\ 29 \)
What is the total length of belting needed for the pulley shown to the right?
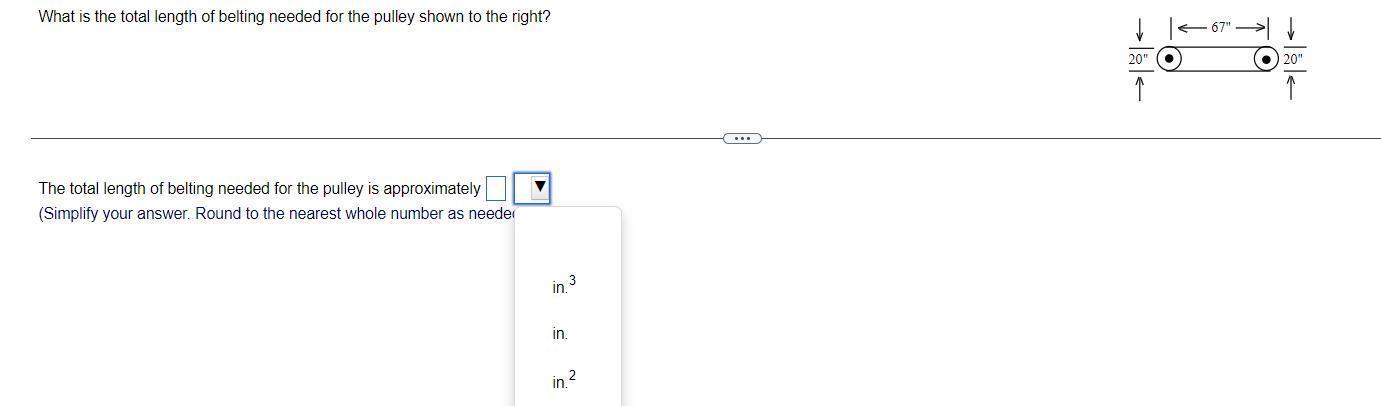
Answers
The diameter of the pulley is given as 20''.
The distance between two pulleys is 67''.
ExplanationTo determine the total length of belting needed for the pulley .
Use the formula.
\(D=2L+(D_L+D_S)\times\frac{\pi}{2}+\frac{(D_L-D_S)^2}{4L}\)Here L is the distance between two pulleys and DL is the diameter of the larger pulley
DS is the diameter of the smaller pulley.
Substitute the values,
\(\begin{gathered} D=2\times67^{\prime}^{\prime}+(20^{\prime}^{\prime}+20^{\prime}^{\prime})\times\frac{\pi}{2}+\frac{(20^{\prime}^{\prime}-20^{\prime}^{\prime})^2}{4\times67^{\prime}^{\prime}} \\ D=134^{\prime}^{\prime}+40^{\prime}^{\prime}\times\frac{\pi}{2}+0 \\ D=134^{\prime}^{\prime}+62.8^{\prime}^{\prime} \\ D=196.8in \end{gathered}\)AnswerHence the total length of belting needed for the pulley is 196.8 in.
In ΔQRS, m∠R = 57°, q = 9, and s = 5. Find the area of ΔQRS.
Answers
The area of ΔQRS is 26.10 square units.
What is triangle?
A triangle is a closed, two-dimensional geometric shape with three straight sides and three angles.
To find the area of \($\triangle QRS$\), we can use the formula:
\($Area = \frac{1}{2} \times base \times height$\)
where the base and height are the length of two sides of the triangle that are perpendicular to each other. We can find these sides using trigonometry.
First, we need to find the length of side \($QR$\). We can use the Law of Cosines:
\($QR^2 = QS^2 + RS^2 - 2(QS)(RS)\cos(R)$\)
where \($R$\) is the angle at vertex \($R$\). Substituting the given values, we get:
\($QR^2 = 9^2 + 5^2 - 2(9)(5)\cos(57^\circ)$\)
\($QR \approx 8.02$\)
Next, we need to find the height of the triangle, which is the perpendicular distance from vertex \($R$\) to side \($QS$\). We can use the sine function:
\($\sin(R) = \frac{opposite}{hypotenuse}$\)
\($\sin(57^\circ) = \frac{height}{8.02}$\)
\($height \approx 6.51$\)
Now we can find the area of the triangle:
\($Area = \frac{1}{2} \times QR \times height$\)
\($Area = \frac{1}{2} \times 8.02 \times 6.51$\)
\($Area \approx 26.10$\) square units
Therefore, the area of \($\triangle QRS$\) is approximately \($26.10$\) square units.
To learn more about triangle visit:
https://brainly.com/question/1058720
#SPJ1
Find 4 + 20, if ü -< -3, -7> and =< 4, -2 >
<-4,-32 >
<7,-3>
<-8, -30
< 5, -11 >
2 0 0 0
Answers
Given statement solution is :- The Vector Calculations and Addition results are as follows:
ü -< -3, -7 > = < -3, -7 >
=< 4, -2 > - < -4, -32 > = < 0, -34 >
< 7, -3 > - < -8, -30 > = < 15, 27 >
< 5, -11 > + < 2, 0, 0, 0 > = < 7, -11, 0, 0 >
And 4 + 20 = 24.
To find the sum of 4 + 20, we simply add the two numbers together:
4 + 20 = 24
As for the given vectors, let's perform the requested calculations:
ü -< -3, -7 > = < -3, -7 >
=< 4, -2 > - < -4, -32 > = < 4 + (-4), -2 + (-32) > = < 0, -34 >
< 7, -3 > - < -8, -30 > = < 7 - (-8), -3 - (-30) > = < 15, 27 >
< 5, -11 > + < 2, 0, 0, 0 > = < 5 + 2, -11 + 0, 0 + 0, 0 + 0 > = < 7, -11, 0, 0 >
Therefore, the Vector Calculations and Addition results are as follows:
ü -< -3, -7 > = < -3, -7 >
=< 4, -2 > - < -4, -32 > = < 0, -34 >
< 7, -3 > - < -8, -30 > = < 15, 27 >
< 5, -11 > + < 2, 0, 0, 0 > = < 7, -11, 0, 0 >
And 4 + 20 = 24.
For such more questions on Vector Calculations and Addition
https://brainly.com/question/31866215
#SPJ11
Find the value of x for which p ll q.

Answers
Answer:
x = 9
Step-by-step explanation:
If p and q are parallel lines then the two angles are alternate interior angles and are equal
9x +8 = 15x - 46
Subtract 9x from each side
9x-9x +8 = 15x -9x - 46
8 = 6x - 46
Add 46 to each side
54 = 6x
Divide by 6
54/6 = 6x/6
9 =x
Answer:
D is the answerExplanation:
This is because you have to first make the equations equal to each other. You do this because you can see that the angles are equal to each other meaning that they are the same amount of degrees. So the equation you will have is (9x + 8) = (15x - 46).
9x + 8 = 15x - 46
You can take off the parenthesis.
Subtract 8 from both sides.
This will lead to
9x = 15x - 54
Then you have to subtract 15x from both sides.
This will have a result of
-6x = -54
When you do this you can see that there are 2 negatives. You can cancel these out. So it will look like
6x = 54
Finally, you have to simplify. Divide both sides by 6.
54/6 = 9 6x/6 = x
The final result is
x = 9So, it can be concluded that the answer is the letter D or the number 9.
Hope this helped
I really need help on this

Answers
Answer:
-27
Step-by-step explanation:
first add 22 to both sides
-x/9=3
then isolate x by multiplying by 9
-x=27
x can't be negative so multiply by -1
x=-27
Answer:
x = -27
Step-by-step explanation:
Solve the equation by inverse operations and you get x = - 27
8a+6ab+5b,-6a-ab-8b and - 4a+2ab+3b
Pls answer this question
Answers
Answer:
4 a+8 ab+8b
Step-by-step explanation:
8 a-4 a+6ab+2ab+5 b+3 b
4 a+8 ab+8b
Fill in the blanks so that the solution of the system is (5, 5).
x + y = −5
y = −x +
Answers
The requried complete system of equation is given as -2x + y = -5 and y = -x + 10.
What is a system of the simultaneous equations?A system of simultaneous equations, also known as a system of equations, is a set of two or more equations that must be solved at the same time. In a system of two equations, for example, the solution is the set of values of the variables that satisfy both equations simultaneously.
Here,
Given equation are
_x + y = −5 - -- - - -(1)
y = −x + _ - - - - - (2)
Now,
Let the coefficient of x in equation 1 is m and the intercept of equation 2 be y,
In equation 1,
Put the given points (5, 5)
m(5) + 5 = - 5
5m = -10
m = -2
Now,
Put the same point equation 2 with C
5 = -5 + C
C = 10
Thus, the requried complete system of equation is given as -2x + y = -5 and y = -x + 10.
Learn more about simultaneous equations here:
https://brainly.com/question/29282797
#SPJ9
Round the numbers in each expression to the nearest whole number.
Then select the expression that can be estimated to 8.
A.
3
1
5
+
5
7
9
B.
1
5
8
+
5
2
5
C.
15
5
7
−
8
2
9
D.
10
1
4
+
1
11
15
Answers
Answer: A, and B
A) 894
B) 728
Step-by-step explanation:
How do I do this equation

Answers
BAD + ABC= 180
(8x+22) + (12x-2) =180
x=8
BAD = (8 x 8 + 22)
8 x 8=64
64 + 22 = 86
Susie walk 10 miles each week. she has already walked 3 miles this week and expects to walk 100 miles how long will it take her to walk 100 miles
Answers
Answer:
10 weeks
Step-by-step explanation: 100÷10=10
big brain
Answer:
9 week and 4 days
Step-by-step explanation:
A) Do the following lengths form a right triangle? Prove it by SHOWING YOUR WORK. 0 6 8 9
Answers
Answer:
friend me on here and imma send you the link Step-by-step explanation:
finding values of products and quotient functions
\(( \frac{r}{s} )(3) = \)
(3) = [/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/fo6qtw13QDITrL0XHWTkFEFXENPGcfQd.jpeg)
Answers
The product and the quotient of the functions are as follows:
(rs)(4) =8
(r / s)(3) = 2
How to solve function?A function relates input and output. It relates an independent variable with a dependent variable.
Therefore, let's solve the function as follows:
r(x) = 2√x
s(x) = √x
Therefore, let's find
(rs)(4) = r(4) × s(4) = 2√4 × √4 = 4 × 2 = 8
Let's find
(r / s)(3) = r(3) / s(3) = 2√3 / √3 = 2
Therefore,
(rs)(4) =8
(r / s)(3) = 2
learn more on function here: https://brainly.com/question/17430065
#SPJ1
Given m || l, find the value of x.

Answers
Answer:
x = 18
Step-by-step explanation:
(6x + 1) and (5x + 19) are corresponding angles and are congruent , then
6x + 1 = 5x + 19 ( subtract 5x from both sides )
x + 1 = 19 ( subtract 1 from both sides )
x = 18
helppppppppppp
4(52x−5)+12x−9
Answers
Answer:
its -1148.
Step-by-step explanation:
remember to use pemdas, do the parentheses first, then add and subtract from left to right
Find the value of a in the triangle shown below.
Answers
Answer: Where is the triangle? There is no picture.
100 Points and I will give brainliest! PLEASE HELP
Prism X is a dilation of Prism Y. The height of Prism X is 10 ⅓ ft, and the volume of Prism X is 74 ⅖ ft³. The height of Prism Y is 5 ⅙ ft.
What is the volume of Prism Y?
Enter your answer as a mixed number in simplest form by filling in the boxes.
Answers
9.3 ft³
height of Prism X is 10 ⅓ ft,the volume of Prism X is 74 ⅖ ft³ height of Prism Y is 5 ⅙ ft.use the rule:
\(\rightarrow \sf (\dfrac{V_1}{V_2} )= (\dfrac{h_1}{h_2} )^3\)
solve:
\(\rightarrow \sf (\dfrac{74\frac{2}{5} }{V_2} )= (\dfrac{10\frac{1}{3} }{5\frac{1}{6} } )^3\)
\(\rightarrow \sf (\dfrac{74\frac{2}{5} }{V_2} )= (2 )^3\)
\(\rightarrow \sf \dfrac{74\frac{2}{5} }{V_2} =8\)
\(\rightarrow \sf V_2 = \dfrac{74\frac{2}{5} }{8}\)
\(\rightarrow \sf V_2 = 9.3 \ ft^3\)
Answer:
Given:
\(\sf Height \ of \ Prism \ X = 10\frac13=\dfrac{(10 \times 3)+1}{3}=\dfrac{31}{3}\)
\(\sf Height \ of \ Prism \ Y = 5\frac16=\dfrac{(5 \times 6)+1}{6}=\dfrac{31}{6}\)
\(\sf Volume\ of \ Prism \ X = 74\frac25=\dfrac{(74 \times 5)+2}{5}=\dfrac{372}{5}\)
Prism X is a dilation of Prism Y.
⇒ Scale factor of dilation = height of Prism X ÷ height of Prism Y
\(\sf =\dfrac{31}{3} \div \dfrac{31}{6}\)
\(\sf =\dfrac{31}{3} \times \dfrac{6}{31}\)
\(\sf =\dfrac63\)
\(\sf =2\)
If Prism X is a dilation of Prism Y by scale factor 2, then Prism Y is a dilation of Prism X by scale factor \(\frac12\).
To find the volume of Prism Y, we simply need to multiply the volume of Prism X by the cube of scale factor \(\frac12\), since volume is measured in cubic units.
\(\sf \implies volume \ of \ Prism \ Y = volume \ of \ Prism \ X \times (scale \ factor)^3\)
\(\sf = \dfrac{372}{5} \times \left(\dfrac12\right)^3\)
\(\sf = \dfrac{372}{5} \times \dfrac18\)
\(\sf =\dfrac{372}{40}\)
\(\sf =\dfrac{93}{10}\)
\(\sf = 9 \frac{3}{10} \ ft^3\)
Help will give thanks to the first to answer

Answers
Answer:
x-4
Step-by-step explanation:
because a number could be x and all you have to do is subtract 4 from a number making it x-4
Answer:
4-x
Step-by-step explanation:
Because it says that x is subtracted from 4 which would make it understood that 4 is the first term and then x.
Darius has at least $15 more than his big brother. Darius's big brother has $72. How much does Darius have?
Answers
Answer:
Darius has $87. I know this because I had the same question.
Step-by-step explanation:
I know this because I had the same question.
Which of the following expressions is equivalent to 3x2 + 6x – 24?
A. 3(x + 2)(x – 4)
B. 3(x – 2)(x + 4)
C. (x + 6)(x – 12)
D. (x – 6)(x + 12)
Answers
3x² + 6x - 24
Simplify 3.
3(x² + 6x - 8)
Think of x² +2x−8. Factor the expression by grouping. First, we need to rewrite the expression as x² + ax + bx - 8. To find a and b, set up a system to be solved.
a + b = 2ab = 1( −8 ) = −8Since ab is negative, a and b have opposite signs. Since a+b is positive, the positive number has a greater absolute value than the negative. Show all pairs of integers whose product is −8.
−1,8−2,4Calculate the sum of each pair.
−1 + 8 = 7−2 + 4 = 2The solution is the pair that gives sum 2
a=−2b=4Rewrite x² + 2x − 8 as (x² − 2x ) + (4x − 8).
(x² − 2x ) + (4x − 8)Simplify x in the first group and 4 in the second.
x ( x − 2) + 4( x − 2 )Simplify the common term x−2 with the distributive property.
( x − 2 )( x + 4 )The entire factored expression is rewritten.
3 ( x − 2 )( x + 4 ) ===> Answer
We conclude that the correct option is "B".
{ Pisces04 }first simplify the 3 from 3,6,-24
that leaves you to have an equation of x^2+2x-8 which you would then use the quadratic formula to get (x-2)(x+4).
don't forget to add the 3 from when you simplified, so it leaves you to have answer of 3(x-2)(x+4)!
DM me if you need me to show the work on paper :D!