Answers
Answer:
Step-by-step explanation:
Although the answer is correct, the Step 3 is not correct.

Related Questions
Hello,
I have paid the $29.00 monthly subscription for my son (jalen); I have signed up only to pay the monthly payment. Sorry to say, he does not live with me. I earlier sent you an email explaining the same with no reply from you. So how does he proceed using his information to freely access your program?
Looking forward to hearing from you shortly.
THANKS,
climacus
Answers
Answer:
Step-by-step explanation:
Help!
What is the answer to this question?

Answers
Answer:
Its perimeter is 23 units
Step-by-step explanation:
The perimeter of any figure is the sum of the lengths of its outline sides
The rule of the distance between two points is:
\(d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\)In the given figure ABCD:
Its perimeter = AB + BC + CD + DE + EA
→ Find the length of each side using the rule above
A = (-4, -2), B = (-1, 2), C = (2, 2), D = (5, -1), E = (2, -4)
→ Substitute them in the rule above to find the lengths of its sides
\(AB=\sqrt{(-1--4)^{2}+(2--2)^{2}}=\sqrt{(-1+4)^{2}+(2+2)^{2}}\\\\=\sqrt{(3)^{2}+(4)^{2}}=\sqrt{9+16}=\sqrt{25}\)
∴ AB = 5
\(BC=\sqrt{(2--1)^{2}+(2-2)^{2}}=\sqrt{(2+1)^{2}+(0)^{2}}\\\\=\sqrt{(3)^{2}+0}=\sqrt{9+0}=\sqrt{9}\)
∴ BC = 3
\(CD=\sqrt{(5-2)^{2}+(-1-2)^{2}}=\sqrt{(3)^{2}+(-3)^{2}}\\\\=\sqrt{9+9}=\sqrt{18}\)
∴ CD = \(\sqrt{18}\)
\(DE=\sqrt{(2-5)^{2}+(-4--1)^{2}}=\sqrt{(-3)^{2}+(-4+1)^{2}}\\\\=\sqrt{(-3)^{2}+(-3)^{2}}=\sqrt{9+9}=\sqrt{18}\)
∴ DE = \(\sqrt{18}\)
\(EA=\sqrt{(-4-2)^{2}+(-2--4)^{2}}=\sqrt{(-6)^{2}+(-2+4)^{2}}\\\\=\sqrt{(-6)^{2}+(2)^{2}}=\sqrt{36+4}=\sqrt{40}\)
∴ EA = \(\sqrt{40}\)
→ Add them to find the perimeter of the figure ABCDE
∴ Its perimeter = 5 + 3 + \(\sqrt{18}\) + \(\sqrt{18}\) +\(\sqrt{40}\) ≅ 22.8098
→ Round it to the whole number
∴ Its perimeter = 23 units
1. Write the angles in order from smallest to largest
45
40.5
R
P
57

Answers
Hello!! :D
Answer: 40.5, 45, 57
Hope this helps! Have a wonderful day! :D
a man buys eggs at RS 9.60 per dozen and sell 20 eggs for RS 18 what is his gain or loss percen?
Answers
Answer:
88.89%
Step-by-step explanation:
Step one:
given
a man buys eggs at RS 9.60 per dozen
what is the unit cost of the dozen of eggs?
unit cost = 9.60/12
= $0.8 per egg
He sold 20 eggs for RS 18
the unit selling price = 18/20
=$0.9 per egg
the percent gain is
=0.8/0.9*100
=0.888*100
=88.89%
Q1 ? Help Robert is 7 ½ years old. How many months old is he?
Answers
Answer:
Step-by-step explanation:
If Robert is 7 1/2 months old you need to multiply 7 1/2 by 12 because there are 12 months in a year.
7x12=84
1/2x12=6
6+84=90
What is the x value such that y=15 - 3x and y = 0
Answers
Add -15 both sides
-3x=-15
Divided by -3 both sides
x=-15/-3
x=5
differentiate y=2-3x/(3-4x)^2
Answers
Answer:
Hope this helps ;) don't forget to rate this answer !
Step-by-step explanation:
To differentiate y = 2 - 3x/(3 - 4x)^2, we can use the quotient rule for differentiation.
The quotient rule states that if f(x) = g(x)/h(x), then the derivative of f(x) is given by:
f'(x) = (g'(x)h(x) - g(x)h'(x)) / h(x)^2
In this case, we can set f(x) = 2 - 3x/(3 - 4x)^2, g(x) = 2, and h(x) = (3 - 4x)^2.
Substituting these values into the formula for the derivative of a quotient, we get:
f'(x) = (2*(3 - 4x)^2 - (2 - 3x)*(-8x)) / (3 - 4x)^4
Simplifying this expression gives:
f'(x) = (-24x^2 + 24x + 6) / (3 - 4x)^3
This is the derivative of y = 2 - 3x/(3 - 4x)^2.
I need the answers for the table below.

Answers
The values of f(x) for the given x - values rounded to 4 decimal places are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013 respectively
Given the function :
tan(πx)/7xSubstitute the given value of x to obtain the corresponding f(x) values :
x = -0.6
f(x) = (tanπ(-0.6))/7(-0.6) = 0.0078358
x = -0.51
f(x) = (tanπ(-0.51))/7(-0.51) = 0.0078350
x = -0.501
f(x) = (tanπ(-0.501))/7(-0.501) = 0.001967
x = -0.5
f(x) = (tanπ(-0.5))/7(-0.5) = 0.001959
x = -0.4999
f(x) = (tanπ(-0.4999))/7(-0.4999) = 0.001958
x = 0.499
f(x) = (tanπ(-0.499))/7(-0.499) = 0.001951
x = -0.49
f(x) = (tanπ(-0.49))/7(-0.49) = 0.00188
x = -0.4
f(x) = (tanπ(-0.4))/7(-0.4) = 0.00125
Therefore, values which complete the table are 0.0078, 0.0078, 0.0020, 0.0020, 0.0019 and 0.0013
Learn more on functions : https://brainly.com/question/12634120
#SPJ1
Mme potatana ask the children to count as a whole class from 1 to 20 Ntate Mafodi asked the children in his class to count seeds from the school's ground in a pile by touching each as they count. in your view support the method that you find important to enhance the strong number sense. Provide appropriate examples for your chosen method.
Answers
The method of counting seeds by touching each can be more effective in enhancing strong number sense in children as it allows them to experience each number physically and helps them in developing a strong sense of numbers.
In order to enhance strong number sense in children, there are various methods that can be used.
In the given scenario, Mme Potatana asked the children to count as a whole class from 1 to 20 while Ntate Mafodi asked the children in his class to count seeds from the school's ground in a pile by touching each as they count.
Both methods have their own benefits, but the method of counting seeds by touching each can be more effective in enhancing strong number sense in children.
The method of counting seeds by touching each can be more effective in enhancing strong number sense in children because it allows them to experience each number physically.
This helps them in developing a strong sense of numbers. By touching each seed as they count, children can feel and see each number, which helps them in understanding numbers better. Additionally, it helps in developing the concept of one-to-one correspondence and counting by rote.
Here are some appropriate examples for enhancing strong number sense using the method of counting seeds by touching each:
1. Use counters: Provide children with counters such as small objects, blocks, or toys. Ask them to count the number of counters by touching each as they count.
2. Counting on fingers: Encourage children to count on their fingers. This helps them in developing a strong sense of numbers and helps them in understanding the concept of one-to-one correspondence.
3. Counting objects in a pile: Ask children to count objects in a pile by touching each as they count. This helps in developing the concept of counting by rote and helps in enhancing strong number sense.
Overall, the method of counting seeds by touching each can be more effective in enhancing strong number sense in children as it allows them to experience each number physically and helps them in developing a strong sense of numbers.
For more such questions on sense of numbers
https://brainly.com/question/31640478
#SPJ8
MrShaggy has 420 bottles of dish soap, MrWings also has 351 bottles of dish soap, MrWings gives all of his soap to MrShaggy, But then MrShaggy gives those soap to MrAmazon, if we subtract 420 by 351, how many dish soaps are in all together?
Answers
Answer: 69
Step-by-step explanation:
420 - 351 = 69
If vectors i+j+2k, i+pj+5k and 5i+3j+4k are linearly dependent, the value of p is what?
Answers
Answer:
\(p = 2\) if given vectors must be linearly independent.
Step-by-step explanation:
A linear combination is linearly dependent if and only if there is at least one coefficient equal to zero. If \(\vec u = (1,1,2)\), \(\vec v = (1,p,5)\) and \(\vec w = (5,3,4)\), the linear combination is:
\(\alpha_{1}\cdot (1,1,2)+\alpha_{2}\cdot (1,p,5)+\alpha_{3}\cdot (5,3,4) =(0,0,0)\)
In other words, the following system of equations must be satisfied:
\(\alpha_{1}+\alpha_{2}+5\cdot \alpha_{3}=0\) (Eq. 1)
\(\alpha_{1}+p\cdot \alpha_{2}+3\cdot \alpha_{3}=0\) (Eq. 2)
\(2\cdot \alpha_{1}+5\cdot \alpha_{2}+4\cdot \alpha_{3}=0\) (Eq. 3)
By Eq. 1:
\(\alpha_{1} = -\alpha_{2}-5\cdot \alpha_{3}\)
Eq. 1 in Eqs. 2-3:
\(-\alpha_{2}-5\cdot \alpha_{3}+p\cdot \alpha_{2}+3\cdot \alpha_{3}=0\)
\(-2\cdot \alpha_{2}-10\cdot \alpha_{3}+5\cdot \alpha_{2}+4\cdot \alpha_{3}=0\)
\((p-1)\cdot \alpha_{2}-2\cdot \alpha_{3}=0\) (Eq. 2b)
\(3\cdot \alpha_{2}-6\cdot \alpha_{3} = 0\) (Eq. 3b)
By Eq. 3b:
\(\alpha_{3} = \frac{1}{2}\cdot \alpha_{2}\)
Eq. 3b in Eq. 2b:
\((p-2)\cdot \alpha_{2} = 0\)
If \(p = 2\) if given vectors must be linearly independent.
Find the volume of this composite solid.
A. 671.96 m3
B. 569.39 m3
C. 56.52 m3
D. 502.4 m3

Answers
Answer:
I think it is 56.52 c because 10 time 4 is 40 in thwn 4 times 4 is 16 in then divide by 2
I need help on this again :(

Answers
Answer:
"Some whole numbers are irrational numbers" False
"Some rational numbers are not whole numbers" True
"Some irrational numbers are not integers" True
"All rational numbers are integers" False
Step-by-step explanation:
Answer:
Step-by-step explanation:
1). False
2). True
3). False (all irrational numbers are not integers)
4). False
PLEASE HELP QUICK!!!!!!!
What is the simplified expression for 2 power 2 multiplied by 2 power 3 over 2 power 4?
A) 2 power 0
B) 2 power 1
C) 2 power 2
D) 2 power 3
Answers
Answer:
\(2^1\)
Step-by-step explanation:
Hello! So, to tackle this problem let's start off with writing out the formula as such! \(\frac{2^2 * 2^3}{2^4}\)
To solve this, what we can do is start off by isolating \(\frac{2^2}{2^4}\) (we can worry about \(2^3\) later). To evaluate \(\frac{2^2}{2^4}\), we're essentially just simplifying the fraction and reducing the exponents. In this case, we can reduce the power of 2 from both the numerator and denominator to get \(\frac{1}{2^2}\) (this is obtained by dividing both numerator and denominator by \(2^2\))
Once we have that, we are now essentially left with \(\frac{2^3}{2^2}\)! From here, we can apply exponent rule, which allows us to get rid of the denominator entirely and now it becomes 2^(3-2). We can subtract the numbers to then simplify it into our answer, \(2^1\) or in other words just 2!
HELP ME ASAP!!! YOU WILL BE BRAINLIEST

Answers
We can conclude that Maya's experimental probabilities fluctuate around the theoretical probability, but over a larger number of trials, the experimental probabilities should converge towards the theoretical probability.
What is probability?
Probability is simply how likely something is to happen. Whenever we're unsure about the outcome of an event, we can talk about the probabilities of certain outcomes—how likely they are. The analysis of events governed by probability is called statistics.
The theoretical probability of rolling a 5 on a fair die is 1/6, which means that if the die is rolled many times, we would expect to see a 5 about 1/6 of the time.
For the first 100 trials, Maya rolled a 5 on 25 of those trials. The experimental probability of rolling a 5 in this case is:
experimental probability = number of 5's rolled / number of trials
experimental probability = 25/100
experimental probability = 0.25
So, in the first 100 trials, Maya's experimental probability of rolling a 5 was 0.25.
For the first 200 trials, Maya rolled a 5 on 30 of those trials. The experimental probability of rolling a 5 in this case is:
experimental probability = number of 5's rolled / number of trials
experimental probability = 30/200
experimental probability = 0.15
So, in the first 200 trials, Maya's experimental probability of rolling a 5 was 0.15.
Comparing these experimental probabilities to the theoretical probability, we see that after 100 trials, Maya's experimental probability of rolling a 5 (0.25) is higher than the theoretical probability (1/6 ≈ 0.167). This suggests that Maya's sample of 100 trials was somewhat biased in favor of rolling a 5.
On the other hand, after 200 trials, Maya's experimental probability of rolling a 5 (0.15) is lower than the theoretical probability (1/6 ≈ 0.167). This suggests that Maya's sample of 200 trials was somewhat biased against rolling a 5.
Overall, we can conclude that Maya's experimental probabilities fluctuate around the theoretical probability, but over a larger number of trials, the experimental probabilities should converge towards the theoretical probability. This is known as the law of large numbers, which states that as the number of trials or observations increases, the experimental probability will tend to approach the theoretical probability.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ1
We might say that Maya's experimental probabilities oscillate about the theoretical probability, but after more trials, the experimental probabilities ought to converge to the theoretical probability.
What is probability?
Simply put, probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes. Statistics is the study of events that follow a probability distribution.
A fair die has a theoretical probability of rolling a 5 of 1/6, therefore if the die is rolled several times, we can anticipate seeing a 5 roughly 1/6 of the time.
For the first 100 trials, Maya rolled a 5 on 25 of those trials. The experimental probability of rolling a 5 in this case is:
experimental probability = number of 5's rolled / number of trials
experimental probability = 25/100
experimental probability = 0.25
So, in the first 100 trials, Maya's experimental probability of rolling a 5 was 0.25.
For the first 200 trials, Maya rolled a 5 on 30 of those trials. The experimental probability of rolling a 5 in this case is:
experimental probability = number of 5's rolled / number of trials
experimental probability = 30/200
experimental probability = 0.15
So, in the first 200 trials, Maya's experimental probability of rolling a 5 was 0.15.
Comparing these experimental probabilities to the theoretical probability, we see that after 100 trials, Maya's experimental probability of rolling a 5 (0.25) is higher than the theoretical probability (1/6 ≈ 0.167). This suggests that Maya's sample of 100 trials was somewhat biased in favor of rolling a 5.
On the other hand, after 200 trials, Maya's experimental probability of rolling a 5 (0.15) is lower than the theoretical probability (1/6 ≈ 0.167). This suggests that Maya's sample of 200 trials was somewhat biased against rolling a 5.
Overall, we can conclude that Maya's experimental probabilities fluctuate around the theoretical probability, but over a larger number of trials, the experimental probabilities should converge towards the theoretical probability. This is known as the law of large numbers, which states that as the number of trials or observations increases, the experimental probability will tend to approach the theoretical probability.
Learn more about probability on:
https://brainly.com/question/13604758
#SPJ1
find the quotient of \(\frac{(x^{3} - 2x^{2} + 6x + 3)}{ (x - 3)}\) using long division
Answers
(x^3 - 2x^2 + 6x + 3)/(x-3)
= (x^3 - 3x^2 + (x^2 - 6x + 9)+ 12x - 6)/(x-3)
= (x^2(x-3) + (x-3)^2 + 6(2x - 1))/x-3
= x^2 + x - 3 + 6(2x - 1)/(x-3)
or
= x^2 + x - 3 remainder 12x - 6
or, in the form p(x) = q(x)d(x) + r(x):
(x^3 - 2x^2 + 6x + 3) = (x^2 + x - 3)(x - 3) + (12x - 6)
which implies that the quotient q(x) = (x^2 + x - 3) and remainder r(x) = 12x - 6
Can someone explain to me why I got this question wrong? The reasoning for my answer (2, 3) for the vertex is because in the setup for the equation f(x) = a( x - h ) + k, x is subtracted from h. If h was negative, it would be adding instead because it'd be a negative and a negative. So I know h is positive. Am I misunderstanding the question? Will give brainliest!

Answers
Kevin's error is that he incorrectly identified the vertex of the parabola as (3, 2) instead of (2, 3), which resulted to the parabola opens downward. The correct vertex is at (2, 3) and the parabola opens upward.
Correcting an Error in Identifying the Vertex and Direction of a Parabola.You are correct that the vertex of the parabola can be determined using the equation f(x) = a(x - h)² + k, where the vertex is at (h, k). In this case, we have f(x) = -(x-2)² + 3, so the vertex can be found by setting x - 2 = 0, which gives x = 2. Plugging this value into the equation,
we get f(2) = -(2-2)² + 3 = 3, so the vertex is at (2, 3).
However, your reasoning for why h is positive is not correct. The expression x - h represents the horizontal distance from the vertex to any point on the parabola. So if x is greater than h, then the expression x - h will be positive, and if x is less than h, then the expression x - h will be negative. In this case, the vertex is at (2, 3), so we have h = 2. This means that any point to the right of the vertex will have a positive value of x - h, while any point to the left of the vertex will have a negative value of x - h.
Therefore, the correct explanation of Kevin's error is that he incorrectly identified the vertex as (3, 2) instead of (2, 3), and as a result, he also incorrectly concluded that the parabola opens downward. In fact, the parabola opens upward because the coefficient of the x² term, -1, is negative.
To know more about the vertex and direction of a parabola,
visit:https://brainly.com/question/20209326
#SPJ1
Translate the phrase into an algebraic equation.
The sum of 5 and x
Answers
Answer:
5+x
Step-by-step explanation:
50 POINTS !!
PLEASE HELP !! ILL GIVE BRAINLIEST TO THE RIGHT ANSWERS.
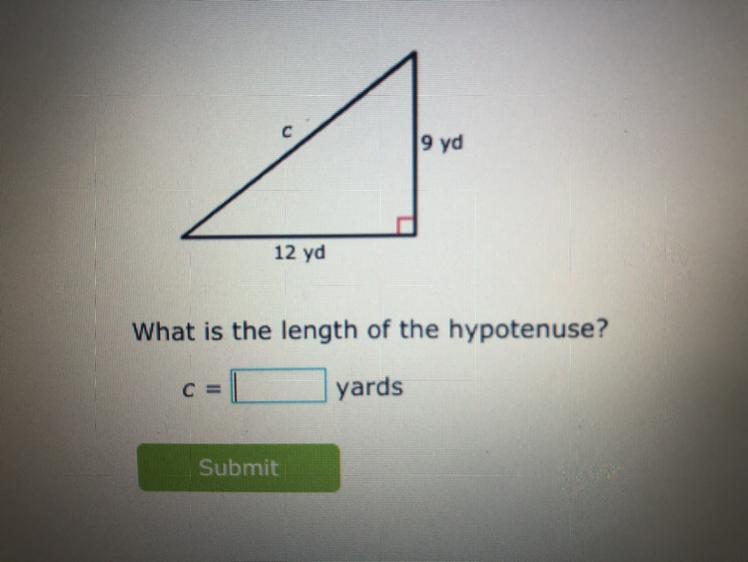
Answers
Answer:
c = 15
Step-by-step explanation:
how many eighths are there in 54/72
Answers
Answer: 6
Step-by-step explanation:
\(\displaystyle\\\frac{54}{72}=\\\\\frac{9(6)}{9(8)}=\\\\\frac{6}{8}=\\\\\frac{1(6)}{8} =\\\\\frac{1}{8}(6)\)
On a bus, the lady sitting in front of me silently passed gas, but why did my mom (who was sitting next to me) silently ask me "did you pass gas" and accuse me??
Answers
Answer: lol she was lowkey trying to call out the lady in front of you without directly addressing her. Or she was just trying to mess with you cuz that's how moms are
Step-by-step explanation:
I need help I don’t understand...

Answers
Answer:
(1 , -2)
Step-by-step explanation:
The intersecting point of two lines is the solution
Answer: X→1(first blank) Y→-2(second blank) and or (1,-2)
The question is asked in the attached file,. Kindly someone answer it in the best way.

Answers
According to the Empirical Rule, 99.7% of the measures fall within 3 standard deviations of the mean in the normal distribution.
What does the Empirical Rule state?The Empirical Rule states that, for a normally distributed random variable, the symmetric distribution of scores is presented as follows:
The percentage of scores within one standard deviation of the mean of the distribution is of approximately 68%.The percentage of scores within two standard deviations of the mean of the distribution is of approximately 95%.The percentage of scores within three standard deviations of the mean off the distribution is of approximately 99.7%.More can be learned about the Empirical Rule at https://brainly.com/question/10093236
#SPJ1
14. Log(x)=2meansa. x=10b. x=2^10c. x=10^2d. x=0e. none of the above
Answers
The absolute value of the dilation factor is the ratio of each side length of the dilated quadrilateral to the corresponding side length of the preimage. How does the ratio of the perimeters in parts B and D compare with the ratio of corresponding side lengths
Answers
9514 1404 393
Answer:
perimeter ratio = dilation factor
Step-by-step explanation:
In general, all linear dimensions are scaled by the dilation factor. This includes lengths of sides, perimeter, circumference, diameter, radius, or any other 1-dimensional (length) measure of a figure.
The ratio of perimeters is equal to the ratio of side lengths.
simplify 18 over 72?
Answers
Answer:
0.25
Step-by-step explanation:
A bride wants her bridesmaids to dress exactly alike. If the dress is $102, the shoes are $79, and the stockings are $22, what does each bridesmaid need to pay
Answers
Answer:203
Step-by-step explanation:
102+79+22 = 203
Answer:
$203
Step-by-step explanation:
Khảo sát 600 sinh viên trường thấy có có 520 sinh viên thích các hoạt động của Hội Thanh Niên nhà trường. Với độ tin cậy 95%, ta có ước lượng tỷ lệ sinh viên toàn trường thích các hoạt động của Hội Thanh Niên thuộc khoảng
Answers
Answer:
I don't know ans OK bro because I can't understand your language what are you writing
What is the best estimate of the perimeter of the figure on the grid if each square has side lengths of 1 mm?
Answers
Answer:
4mm
Step-by-step explanation:
you have to add both sides after substituting each of the 4 sides by 1mm
which gives you the total of 4
A hat contains 35 marbles. Of them, 20 are red and 15 are green. If one marble is randomly selected out of this hat, what is the probability that this marble is red? Round your answer to two decimal places. P(A) =
Answers
Answer:
P(A) = 0.57 (rounded to two decimal places).
Step-by-step explanation:
The probability of selecting a red marble from the hat can be found by dividing the number of red marbles by the total number of marbles:
P(red) = number of red marbles / total number of marbles
P(red) = 20/35
We can simplify this fraction by dividing both the numerator and denominator by 5:
P(red) = 4/7
So the probability of selecting a red marble from the hat is 4/7, or approximately 0.57 when rounded to two decimal places.
Therefore, P(A) = 0.57 (rounded to two decimal places).
