I EILL MAKE BRAINLEST NEED HELP ASAP MT TEACHER IS ABOUT TO YELL WT ME PLEASE PLEASE PLEASE PLEASE PLEASE

Answers
Related Questions
Expand each logarithm as much as possible to rewrite each expression as a sum, difference or product of logs.

Answers
In order to expand this logarithm, we can use the following property:
\(\log_a(b\cdot c)=\log_ab+\log_ac\)So, expanding the given logarithm, we have:
\(\begin{gathered} \log_b(7x\cdot2y)\\ \\ =\log_b7x+\log_b2y\\ \\ =\log_b7+\log_bx+\operatorname{\log}_b2+\operatorname{\log}_by \end{gathered}\)exercise 1.1.8. (harder) solve y″=sinx for ,y(0)=0, .
Answers
Step-by-step explanation:
y'' = sinx
y' = -cosx + k
y = -sinx + kx + c if y(0) = 0 then c = 0
y = - sin x + kx Where k is a constant
What comes next in the following series?

Answers
The next number in the series is 30.
What is series?It should be noted that series simply means the operation of adding values together in a data set.
In this case, it can be seen that the numbers are interchangeable between 30 and 31.
In this case, since 31 was the last number, the next number will be 30.
Learn more about series on:
brainly.com/question/24295771
#SPJ1
Select the function that is odd.
A. f (x) = sin (x)
B. f (x) = cos (x) + sin (x)
C. f (x) = cos^3 (x)
D. f (x) = sin^2 (x)
Answers
DUE FRIDAY PLEASE HELP WELL WRITTEN ANSWERS ONLY!!!!
The value of tan(3π/4) is -1. How does the value of tan(3π/4 + 7π) compare? Explain your reasoning.
Answers
Tan(3/4 - \(\pi\) ) = 1, which is the ratio of a right triangle with a 45° angle's opposite side to its adjacent side. This is different from value of \(tan(3\pi /4)\), which is -1, it corresponds to a different angle.
The tangent of the angle 3/4 (or 135 degrees) is equal to -1 because \(tan(3/4)\)has a value of -1. The ratio of the opposite side to the adjacent side can be calculated by drawing a right triangle with an angle of 135 degrees.
To obtain the value of\(tan(3\pi /4 - \pi )\), we first need to simplify the phrase \(3\pi /4 - \pi\), which gives us\(\pi /4\) (or 45 degrees). Therefore, we need to find the tangent of the angle 45 degrees.
The ratio of the opposite side to the adjacent side of a right triangle with a 45-degree angle has the value of \(tan(45)\), which is equal to 1.
So, \(tan(3\pi /4 – \pi ) = tan(\pi /4) = 1.\)
In summary, the value of\(tan(3\pi/4 - \pi)\)) is equal to 1, which is the ratio of the opposite side to the adjacent side of a right triangle with an angle of 45 degrees. This is distinct from the value of \(tan(3\pi /4)\), which is -1, as it corresponds to a different angle.
Learn more about tan here:
https://brainly.com/question/14347166
#SPJ1
number 2, help plz i don’t get it

Answers
Answer:
b
Step-by-step explanation:
2y + 40 and 60 are same- side exterior angles and sum to 180° , that is
2y + 40 + 60 = 180
2y + 100 = 180 ( subtract 100 from both sides )
2y = 80 ( divide both sides by 2 )
y = 40
How does the stem-and-leaf plot show the distribution of these data? O A. The lengths of the rows are similar to the widths of bars in a histogram; longer rows of data correspond to higher freque OB. The lengths of the rows are similar to the heights of bars in a histogram; longer rows of data correspond to higher freque OC. The lengths of the rows are similar to the widths of bars in a histogram; longer rows of data correspond to smaller freque O D. The lengths of the rows are similar to the heights of bars in a histogram; longer rows of data correspond to smaller freque
Answers
The stem-and-leaf plot shows that the lengths of the bars in a histogram are similar to the lengths of the rows, and long rows of data suggest higher frequency.
The stem-and-leaf plot is a type of graphical representation used to plot and display the collection of numbers. The leaf is used to represent the one's place of the digit. And the stem is used to represent the tens place of the digit. It is represented in tabular data organized into discrete numerical categories.
The main advantage of this plot is that it helps to organize a large set of data values. They are also used to determine the median and mode. But they are not very informative for a small set of data. When this plot is compared to the histogram, the length of the rows of this plot is similar to the height of the bars in the histogram. So that the longer row of this plot corresponds to the higher frequency. So the correct statement is option A.
To know more about stem-and-leaf plots:
https://brainly.com/question/26630412
#SPJ4
what is yhe answer?????

Answers
161%
Step-by-step explanation:
They are asking percentage so we know we going to ×100%
4943 AS A PERCENTAGE OF 3076
\( \frac{4943}{3076} \times 100 \)
161%
16 Select the correct answer. An ounce of cheese can be estimated by: A. One hand cupped. B. The size of your fist. C. The size of the palm of your hand. D. The size of your thumb.
Answers
Answer:
D
Step-by-step explanation:
help me please I donr understand this

Answers

Answer:
x<7/12
Step-by-step explanation:
you have to get X by its self so you take the 1/4 and subtract it from both sides
The mean exam score for 49 male high school students is 239 and the population standard deviation is 47 The mean exam score for 53 female high school students is 21.1 and the population standard deviation is 4.3. At α=001, can you reject the claim that male and female high school students ha equal exam scores? Complete parts (a) through (e). Click here to view page 1 of the standard normal distribution table. Click here to view. page 2 of the standard normal distribution table. A. Male high school students have lower exam scores than female students B. Male and temale high school students have different exam scores. C. Male and female high school students have equal exam scores D. Male high school students have greater exam scores than female students
Answers
Comparing the means of the two samples, we find that the difference between the means is significant. Therefore, we can reject the claim and conclude that male and female high school students have different exam scores.
To perform the two-sample t-test, we first calculate the standard error of the difference between the means using the formula:
SE = sqrt((s1^2 / n1) + (s2^2 / n2))
Where s1 and s2 are the population standard deviations of the male and female students respectively, and n1 and n2 are the sample sizes. Plugging in the values, we have:
SE = sqrt((47^2 / 49) + (4.3^2 / 53))
Next, we calculate the t-statistic using the formula:
t = (x1 - x2) / SE
Where x1 and x2 are the sample means. Plugging in the values, we have:
t = (239 - 21.1) / SE
We can then compare the t-value to the critical t-value at α = 0.01 with degrees of freedom equal to the sum of the sample sizes minus 2. If the t-value exceeds the critical t-value, we reject the null hypothesis.
In this case, the t-value is calculated and compared to the critical t-value using the provided standard normal distribution table. Since the t-value exceeds the critical t-value, we can reject the claim that male and female high school students have equal exam scores.
Therefore, the correct answer is:
B. Male and female high school students have different exam scores.
Learn more about hypothesis testing here: brainly.com/question/17099835
#SPJ11
A farmer bought a goat for Rs 15000 and a cow for Rs 35000. If he sold the goat at 10% profit and cow at 20% loss, find his profit or loss percent in whole transaction.
Answers
He sold the goat at 2 10% profit so he sold the goat for: 15,000 x 1.10 = 16,500
He sold the cow for a loss, so he sold the cow for 35000 x 0.80 = 28,000
Total he paid for both: 15,000 + 35,000 = 50,000
Total he sold both for: 16,500 + 28,000 = 44,500
He sold them for less than what he paid so he lost money.
Subtract sold amount from bought amount:
50,000 - 44,500 = 5,500
Divide the difference by the amount he paid:
5,500 / 50,000 = 0.11 x 100 = 11%
His loss percentage was 11%
Find the area of the part of the plane 3x 2y z = 6 that lies in the first octant.
Answers
The area of the part of the plane 3x 2y z = 6 that lies in the first octant is mathematically given as
A=3 √(4) units ^2
What is the area of the part of the plane 3x 2y z = 6 that lies in the first octant.?Generally, the equation for is mathematically given as
The Figure is the x-y plane triangle formed by the shading. The formula for the surface area of a z=f(x, y) surface is as follows:
\(A=\iint_{R_{x y}} \sqrt{f_{x}^{2}+f_{y}^{2}+1} d x d y(1)\)
The partial derivatives of a function are f x and f y.
\(\begin{aligned}&Z=f(x)=6-3 x-2 y \\&=\frac{\partial f(x)}{\partial x}=-3 \\&=\frac{\partial f(y)}{\partial y}=-2\end{aligned}\)
When these numbers are plugged into equation (1) and the integrals are given bounds, we get:
\(&=\int_{0}^{2} \int_{0}^{3-\frac{3}{2} x} \sqrt{(-3)^{2}+(-2)^2+1dxdy} \\\\&=\int_{0}^{2} \int_{0}^{3-\frac{3}{2} x} \sqrt{14} d x d y \\\\&=\sqrt{14} \int_{0}^{2}[y]_{0}^{3-\frac{3}{2} x} d x d y \\\\&=\sqrt{14} \int_{0}^{2}\left[3-\frac{3}{2} x\right] d x \\\\\)
\(&=\sqrt{14}\left[3 x-\frac{3}{2} \cdot \frac{1}{2} \cdot x^{2}\right]_{0}^{2} \\\\&=\sqrt{14}\left[3-\frac{3}{2} \cdot \frac{1}{2} \cdot x^{2}\right]_{0}^{2} \\\\&=\sqrt{14}\left[3.2-\frac{3}{2} \cdot \frac{1}{2} \cdot 3^{2}\right] \\\\&=3 \sqrt{14} \text { units }{ }^{2}\)
In conclusion, the area is
A=3 √4 units ^2
Read more about the plane
https://brainly.com/question/1962726
#SPJ4
What term must go in the space to complete the statement

Answers
Answer:
5v+35 = 5(v+7)
Step-by-step explanation:
5(v+7) = 5v+35
Answer:
5
Step-by-step explanation:
Because
5(v+7)
5v+35..
hope it helps
Find the solution to this initial value problem. dy TU + 5 cot(5x) y = 3x³-1 csc(5x), y = 0 dx 10 Write the answer in the form y = f(x)
Answers
The solution to the initial value problem can be written in the form:
y(x) = (1/K)∫|sin(5x)|⁵ (3x³ - csc(5x)) dx
where K is a constant determined by the initial condition.
To solve the initial value problem and find the solution y(x), we can use the method of integrating factors.
Given: dy/dx + 5cot(5x)y = 3x³ - csc(5x), y = 0
Step 1: Recognize the linear first-order differential equation form
The given equation is in the form dy/dx + P(x)y = Q(x), where P(x) = 5cot(5x) and Q(x) = 3x³ - csc(5x).
Step 2: Determine the integrating factor
To find the integrating factor, we multiply the entire equation by the integrating factor, which is the exponential of the integral of P(x):
Integrating factor (IF) = e^{(∫ P(x) dx)}
In this case, P(x) = 5cot(5x), so we have:
IF = e^{(∫ 5cot(5x) dx)}
Step 3: Evaluate the integral in the integrating factor
∫ 5cot(5x) dx = 5∫cot(5x) dx = 5ln|sin(5x)| + C
Therefore, the integrating factor becomes:
IF = \(e^{(5ln|sin(5x)| + C)}\)
= \(e^C * e^{(5ln|sin(5x)|)}\)
= K|sin(5x)|⁵
where K =\(e^C\) is a constant.
Step 4: Multiply the original equation by the integrating factor
Multiplying the original equation by the integrating factor (K|sin(5x)|⁵), we have:
K|sin(5x)|⁵(dy/dx) + 5K|sin(5x)|⁵cot(5x)y = K|sin(5x)|⁵(3x³ - csc(5x))
Step 5: Simplify and integrate both sides
Using the product rule, the left side simplifies to:
(d/dx)(K|sin(5x)|⁵y) = K|sin(5x)|⁵(3x³ - csc(5x))
Integrating both sides with respect to x, we get:
∫(d/dx)(K|sin(5x)|⁵y) dx = ∫K|sin(5x)|⁵(3x³ - csc(5x)) dx
Integrating the left side:
K|sin(5x)|⁵y = ∫K|sin(5x)|⁵(3x³ - csc(5x)) dx
y = (1/K)∫|sin(5x)|⁵(3x³ - csc(5x)) dx
Step 6: Evaluate the integral
Evaluating the integral on the right side is a challenging task as it involves the integration of absolute values. The result will involve piecewise functions depending on the range of x. It is not possible to provide a simple explicit formula for y(x) in this case.
Therefore, the solution to the initial value problem can be written in the form: y(x) = (1/K)∫|sin(5x)|⁵(3x³ - csc(5x)) dx
where K is a constant determined by the initial condition.
To learn more about product rule visit:
brainly.com/question/29198114
#SPJ11
The SC Electric Company has bid on two electrical wiring jobs. The owner of the company believes that
• the probability of being awarded the first job (Event A) is 0.75;
• the probability of being awarded the second job (Event B) is 0.5; and
• the probability of being awarded both jobs (A and B) is 0.375.
If the owner's beliefs are correct, which of the following statements must be true concerning event A and event B?
Answers
If the owner's beliefs are correct, the probability of being awarded the second job (Event B) is 0.5 . Event A and Event B are not mutually exclusive and are independent and must be true for event A and event B.
Simply put, the probability is the likelihood that something will occur. When we don't know how an event will turn out, we can discuss the likelihood or likelihood of several outcomes.
By simply dividing the favorable number of possibilities by the entire number of possible outcomes, the probability of an occurrence can be determined using the probability formula. Because the favorable number of outcomes can never exceed the entire number of outcomes, the chance of an event occurring might range from 0 to 1. Additionally, the proportion of positive outcomes cannot be negative. In the sections that follow, let's go into greater detail on the fundamentals of probability.
Know more about probability at:
brainly.com/question/24756209
#SPJ4
At what point on the graph is the rate of reaction the greatest?
Answers
The instantaneous rate at the beginning of a reaction, or when t = 0, is known as the starting rate of the reaction.
What is rate of Reaction ?The rate at the beginning of the reaction may be determined using the graph of change in product over time or change in reactant over time. The highest rate on the curve is the beginning rate. Since the reactants are concentrated at their highest at the beginning, the most collisions are occurring.
Rates of response can be depicted in graphs. To depict the pace of reaction, we may create a graph of product (or reactant) against time. The pace of reaction will be the gradient of the graph. The pace of response increases with increasing gradient steepness.
The instantaneous rate at the beginning of a reaction, or when t = 0, is known as the starting rate of the reaction. The beginning rate is equal to the slope of the reactant concentration versus time curve at time zero, which is negative.
To learn more about The rate of reaction refer to :
https://brainly.com/question/28989045
#SPJ4
the following table gives the round-trip commute time for a selection of employees at a large company complete the stem and leaf plot below use the tens place as the stem and use the one place as delete describe the shape of distribution
Answers
From the given table, let's complete the stem and leaf plot.
Part (a):
From the given table, we have 27 data.
It consists of just the data for the round-trip commute time for the employees.
Therefore, data were collected for 1 quantitative variable.
Part (b):
The data constitute a sample
Part (c):
To compute the stem and leaf plot, we have:
Stems------------->Leaves
5--------------------> 0, 0, 3, 3, 3, 4, 7, 7, 9
6----------------------> 0, 1, 3, 4, 5, 7, 8, 8
7------------------------> 0, 3, 4, 4, 5
8------------------------>0, 1, 9
9-------------------------> 0, 4
Part d:
The shape of the data can be said to be right skewed .
A right triangle had a base of 7 feet and a height of 24feet. Which measurement represents the length of the hypotenuse
Answers
Answer:Hypotenuse = 25 feet
Step-by-step explanation:Pythagorean Theorem: 7^2 + 24^2 = 625
The square root of 625 is 25.
help pls and thanks
pick

Answers
Answer:
55/9
Step-by-step explanation:
six less than twice a number x is 38 whats the value ofx
Answers
Answer:
x=22
Step-by-step explanation:
We would do the opposite so "six less" we would add 6 to 38. 6+38= 44 and "twice a number" we would divide by 2. 44 /2= 22. So the answer would be 22.
Hope this helps! :)
Answer:
Answer is 22
Step-by-step explanation:
38+6=44
44 ÷ 2= 22
:)
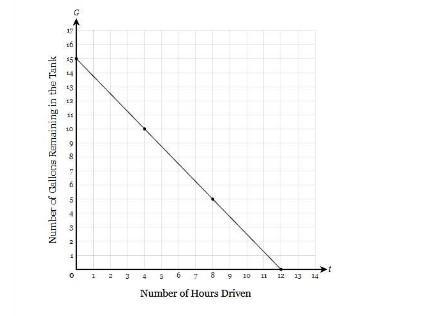
Serenity filled up her car with gas before embarking on a road trip across the country. Let � G represent the number of gallons of gas remaining in her gas tank after driving for � t hours. A graph of � G is shown below. Write an equation for � G then state the � y-intercept of the graph and determine its interpretation in the context of the problem.
Answers
The equation is: G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
How to find the linear equation of the graph?The formula for the equation of a line in slope intercept form is:
y = mx + c
where:
m is slope
c is y-intercept
From the graph, we see that:
y-intercept = 15 gallons
Now, the slope is gotten from the formula:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (10 - 5)/(4 - 8)
Slope = -⁵/₄
Thus, equation is:
G = -⁵/₄t + 15
The slope of the function represents that ⁵/₄ gallons of gas is consumed to drive the car for one hour.
Read more about Linear equation graph at: https://brainly.com/question/28732353
#SPJ1
Find the center of mass of the areas formed by 2y^(2)-x^(3)=0 between 0≤ x ≤ 2
Answers
We need to calculate the coordinates of the center of mass using the formula for a two-dimensional object.
First, let's rewrite the equation 2y^2 - x^3 = 0 in terms of y to find the boundaries of the curve. Solving for y, we have y = ±(x^3/2)^(1/2) = ±(x^3)^(1/2) = ±x^(3/2).
Since the curve is symmetric about the x-axis, we only need to consider the positive portion of the curve, which is y = x^(3/2).
To find the center of mass, we need to calculate the area of each segment between x = 0 and x = 2. The area can be found by integrating the function y = x^(3/2) with respect to x:
A = ∫[0, 2] x^(3/2) dx = [(2/5)x^(5/2)]|[0, 2] = (2/5)(2)^(5/2) - (2/5)(0)^(5/2) = (4/5)√2.
Next, we need to calculate the x-coordinate of the center of mass (Xcm) and the y-coordinate of the center of mass (Ycm):
Xcm = (1/A)∫[0, 2] (x * x^(3/2)) dx = (1/A)∫[0, 2] x^(5/2) dx = (1/A)[(2/7)x^(7/2)]|[0, 2] = (1/A)((2/7)(2)^(7/2) - (2/7)(0)^(7/2)) = (8/35)√2.
Ycm = (1/2A)∫[0, 2] (x^2 * x^(3/2)) dx = (1/2A)∫[0, 2] x^(7/2) dx = (1/2A)[(2/9)x^(9/2)]|[0, 2] = (1/2A)((2/9)(2)^(9/2) - (2/9)(0)^(9/2)) = (32/45)√2.
Therefore, the center of mass is approximately (Xcm, Ycm) = (8/35)√2, (32/45)√2).
Learn more about center of mass here:
https://brainly.com/question/27549055
#SPJ11
What is the meaning of life, the universe, and everything?
Answers
Answer:
meaning of life is life
Answer:
a common name for the off-topic section of an Internet forum and the phrase is invoked in similar ways to mean. when asked about the meaning of life, will answer "42". Several online calculators are also programmed with the Question.
Step-by-step explanation: 42find the points on the ellipse 4x2 y2 = 4 that are farthest away from the point (1, 0). (x, y) = (smaller y-value) (x, y) = (larger y-value)
Answers
The points on the ellipse 4x^2 + y^2 = 4 that are farthest away from the point (1, 0) are (x, y) = (0, -2) with the smaller y-value and (x, y) = (0, 2) with the larger y-value.
The ellipse equation is given as 4x² + y² = 4. We are required to find the points on this ellipse that are farthest away from the point (1, 0). Solution: Given, the equation of ellipse 4x² + y² = 4Putting (1, 0) on the equation, we get; 4(1)² + (0)² = 4 ⇒ 4 + 0 = 4, which is a point on the ellipse. So, (1, 0) is on the ellipse. Hence, we are required to find the point on the ellipse that is farthest away from the point (1, 0).Let's take the equation in the form of x²/a² + y²/b² = 1.4x² + y² = 4 => x²/(4/√4) + y²/(4/1) = 1Let a = 2/1 and b = 2/√4 = 1Hence, the semi-major axis is 2 and semi-minor axis is 1.We know that the distance between two points P(x1, y1) and Q(x2, y2) is given by √[(x2 − x1)² + (y2 − y1)²].For the farthest point from the given point (1, 0), we need to find the point on the major axis that intersects with the ellipse. This point will be on the top-right and bottom-left of the ellipse, at a distance of a from the center. And, the distance between this point and (1, 0) will be a distance of c from the center. As we have the value of a, we need to find c. We know that the value of c is given by √(a² − b²).Hence, c = √(a² − b²) = √(4 − 1) = √3.Now, let's find the farthest point from (1, 0) using the formulae above.We have a = 2 and c = √3. Therefore, the coordinates of the required points are:(x, y) = (1, √(3)) and (1, −√(3))So, the required points on the ellipse are (1, √(3)) and (1, −√(3)).Hence, (x, y) = (smaller y-value) is (1, −√(3)) and (x, y) = (larger y-value) is (1, √ (3)).
Learn more about points here:
https://brainly.com/question/29509250
#SPJ4
The two points on the ellipse that are farthest away from (1,0) are (-1,0) and \(( \frac{ - 1}{3} , 2 \sqrt( \frac{2}{3})) \: or \: (\frac{ - 1}{3} , - 2 \sqrt( \frac{2}{3})) \)
How to find the points on the ellipse?
To find the points on the ellipse that are farthest away from the point (1,0), we first need to find the distance between the point (1,0) and any point (x,y) on the ellipse. The distance between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by the formula:\(d = \sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2)\)
Using this formula, we can find the distance between (1,0) and any point (x,y) on the ellipse 4x² + y² = 4 as:\(d = \sqrt((x - 1)^2 + y^2)\)
To find the points on the ellipse that are farthest away from (1,0), we need to maximize this distance function subject to the constraint 4x² + y² = 4. To do this, we can use the method of Lagrange multipliers.
Let f(x,y) = (x - 1)² + y² be the distance function and g(x,y) = 4x² + y² - 4 be the constraint function. The Lagrange function is given by:
L(x,y,λ) = f(x,y) - λ g(x,y)
Taking the partial derivatives of L with respect to x, y, and λ and setting them to zero, we get:
2(x - 1) - 8λx = 0
2y - 2λy = 0
4x² + y² - 4 = 0
From the second equation, we get y(1 - λ) = 0, which gives us two cases:
Case 1: y = 0
From the third equation, we get 4x² = 4, which gives us x = ±1. Therefore, the two points on the ellipse with y = 0 that are farthest away from (1,0) are (1,0) and (-1,0).
Case 2: λ = 1
Substituting λ = 1 into the first and third equations, we get:
2(x - 1) - 8x = 0
4x² + y² - 4 = 0
Simplifying the first equation, we get x = -1/3. Substituting this into the second equation, we get \(y = ±2 \sqrt( \frac{2}{3})\)
. Therefore, the two points on the ellipse with λ = 1 that are farthest away from (1,0) are (-1/3, 2sqrt(2)/3) and \((-1/3, -2 \sqrt \frac{2}{3})\).
Thus, the two points on the ellipse that are farthest away from (1,0) are (-1,0) and
\(( \frac{ - 1}{3} , 2 \sqrt( \frac{2}{3})) \: or \: (\frac{ - 1}{3} , - 2 \sqrt( \frac{2}{3})) \)
Learn more about ellipse here,
https://brainly.com/question/16904744
#SPJ1
Correct question is "find the points on the ellipse 4x²+ y² = 4 that are farthest away from the point (1, 0). (x, y) = (smaller y-value) (x, y) = (larger y-value)."
Find the value of x. Write your answer in simplest form.

Answers
Answer:
It would be 4.
Step-by-step explanation:
Alright, this is a 30-60-90 special triangle. With special triangles, there is a formula that you can use to find unknown side lengths of a triangle if you know the angles of it.
With a 30-60-90 triangle, the sides opposite of these angles are:
30 degrees : x
60 degrees: x√3
90 degrees: 2x
With this, we can see that opposite of the 60 degrees is the length 2√3. From this, it can be found that the opposite of the 30 degrees would be 2, given the formula of the special triangle. Lastly, the unknown value would be 4, since it is two times this amount.
Answer:
x = 4
Step-by-step explanation:
Using the sine ratio in the right triangle and the exact value
sin60° = \(\frac{\sqrt{3} }{2}\) , then
sin60° = \(\frac{opposite}{hypotenuse}\) = \(\frac{2\sqrt{3} }{x}\) = \(\frac{\sqrt{3} }{2}\) ( cross- multiply )
\(\sqrt{3}\) x = 4\(\sqrt{3}\) ( divide both sides by \(\sqrt{3}\) )
x = 4
Examples of substantive procedures include _______. A. observation B. inquiry C. All of these answer choices are correct. D. confirmation
Answers
Examples of substantive procedures, which are used in auditing, include observation, inquiry, confirmation, and more.
Substantive procedures are specific audit procedures performed to gather evidence and assess the reasonableness of financial statement assertions. These procedures aim to obtain substantive evidence about the accuracy, completeness, and validity of the financial information.
Examples of substantive procedures include observation, where auditors directly witness a process or activity, such as counting physical inventory. Inquiry involves seeking information from management or other personnel regarding financial transactions or events. Confirmation refers to the direct communication with third parties, such as banks or customers, to verify the accuracy of reported balances or transactions.
Other examples of substantive procedures include analytical procedures, inspection of records and documents, and reperformance of calculations or controls. Therefore, all answer choices (A. observation, B. inquiry, C. All of these answer choices are correct, and D. confirmation) are valid examples of substantive procedures in auditing.
Learn more about auditing here:
https://brainly.com/question/14652228
#SPJ11
The equation X^2/16 + y^2/9 = 1 defines an ellipse, which is graphed above. In this excercise we will approximate the area of this ellipse. (a) To get the total area of the ellipse, we could first find the area of the part of the ellipse lying in the First Quadrant, and then multiply by what factor? (b) Find the function y=f(x) that gives the curve bounding the top of the ellipse. (c) Use deltax=1 and midpoints to approximate the area of the part of the ellipse lying in the First Quadrant. (d) Approximate the total area of the ellipse.
Answers
To approximate the area of the ellipse defined by the equation x^2/16 + y^2/9 = 1, we can follow these steps.
(a) To find the total area of the ellipse, we first calculate the area of the part lying in the First Quadrant. Then, we multiply this area by 4 since the ellipse is symmetric about both the x-axis and the y-axis. Multiplying by 4 accounts for the remaining three quadrants, resulting in the total area of the ellipse.
(b) To find the curve bounding the top of the ellipse, we solve the given equation for y. By rearranging the equation, we get y = f(x) = 3√(1 - (x/4)^2), where f(x) represents the upper boundary of the ellipse.
(c) Using a midpoint approximation, we can estimate the area of the part of the ellipse lying in the First Quadrant. We divide the x-axis into equal intervals of width Δx = 1 and calculate the corresponding y-values using the function y = f(x). Then, we approximate the area of each rectangle formed by Δx and the corresponding y-value, summing up these areas for all intervals.
(d) To approximate the total area of the ellipse, we multiply the estimated area from part (c) by 4 since we considered only the First Quadrant. The result provides an approximation of the total area of the ellipse.
Learn more about ellipse here : brainly.com/question/20393030
#SPJ11
Work out and simplify where possible

Answers
I hope it helps you ❤️❤️❤️

Answer:
a= 13/18 and b=5/16
Step-by-step explanation:
in A, multiply 4/9 by 2, you get 8/18 then add to it 5/18 you get 13/18
in B, multiply 3/8 by 2, you get 6/16 then subtract it by 1/16, you get 5/16
A cake shop bakes a variety of brownies. the top-selling brownies are ones with toppings of chocolate chip, walnuts, or both. a customer enters the store. the probability that the customer will pick both toppings is 0.4. what is the probability that they will pick neither the chocolate chip nor the walnut toppings? a. 0.5 b. 0.3 c. 0.45 d. 0.8 e. 0.2
Answers
Based on the probabilities that a customer will pick chocolate chip, walnut, or both, the probability that the customer will pick neither is 0.3.
What is the probability of picking neither chocolate chip or walnut?This can be found by the formula:
= 1 - (Probability of picking chocolate chip + Probability of picking walnut + Probability of picking both)
Solving gives:
= 1 - (0.2 + 0.1 + 0.4)
= 1 - 0.7
= 0.3
Find out more on probabilities at https://brainly.com/question/1691063.
#SPJ4

Answer:
0.3
Step-by-step explanation: