Answers
Answer:
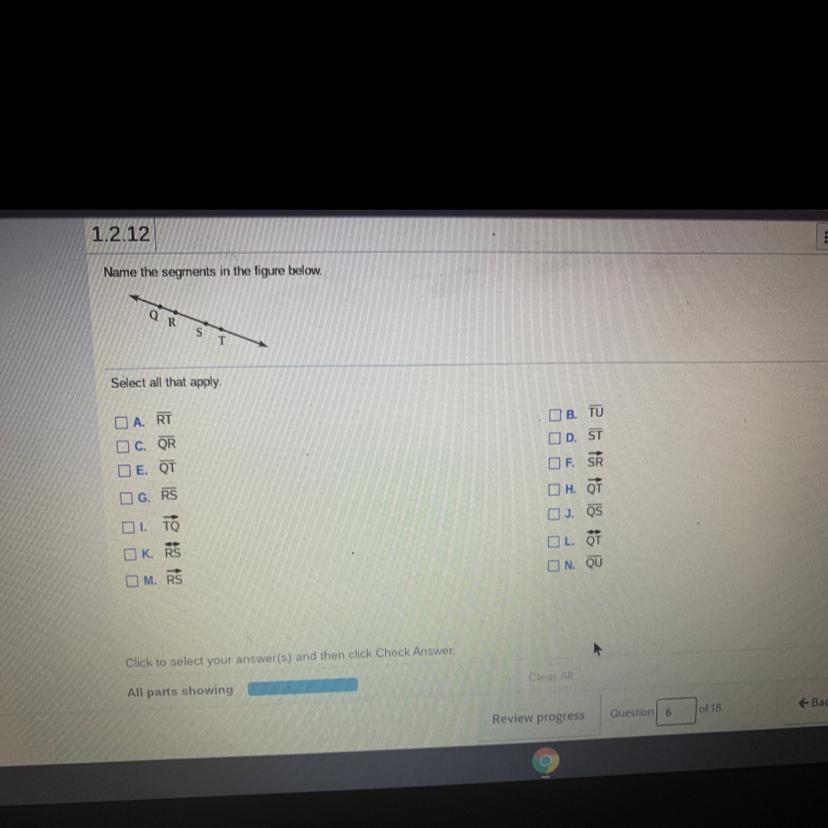
The answer is QR,RS, and ST
Step-by-step explanation:
i hope this helps .
Explanation:
Related Questions
For what value of the variable: 1. are the values of the expressions 2m−13 and m+3 equal? 2. is the value of 2x+1 twenty greater than 8x+5? 3. is the value of 9−y twice as much as the value of y?
Answers
Answer:
1.- m = 13
2.- \(x<-\frac{2}{3}\)
3.- y = 3
Step-by-step explanation:
In all cases we need to start with an equation or an inequality and slove for the variable:
Case 1. : 2 m - 13 = m + 3
\(2m-13=m+3\\2m-m=3+13\\m=16\)
Case 2. : 2 x + 1 > 8 x + 5 + 20
\(2x+1>8x+25\\1-25>8x-2x\\-24>6x\\-4 >x\\x<-4\)
Case 3. : 9 - y = 2 y
\(9-y=2y\\9=2y+y\\9=3y\\y=3\)
Determine the turning points and distinguish between them when necessary y=x³ - 3x - 9x + 4
Answers
The turning points of the function y = x³ - 3x² - 9x + 4 are (3, -23) and (-1, 9).
To determine the turning points of the given function y = x³ - 3x² - 9x + 4, we need to find the critical points where the derivative of the function is equal to zero.
1. Find the derivative of the function:
y' = 3x² - 6x - 9
2. Set the derivative equal to zero and solve for x:
3x² - 6x - 9 = 0
3. Factorize the quadratic equation:
3(x² - 2x - 3) = 0
4. Solve the quadratic equation by factoring or using the quadratic formula:
(x - 3)(x + 1) = 0
This gives us two possible values for x: x = 3 and x = -1.
5. Substitute these critical points back into the original function to find the corresponding y-values:
For x = 3:
y = (3)³ - 3(3)² - 9(3) + 4
= 27 - 27 - 27 + 4
= -23
For x = -1:
y = (-1)³ - 3(-1)² - 9(-1) + 4
= -1 - 3 + 9 + 4
= 9
6. Therefore, the turning points are (3, -23) and (-1, 9).
Note: It appears that there was a typo in the original equation, where the term "-9x" should have been "-3x²". The above solution assumes the corrected equation.
For more such questions on points, click on:
https://brainly.com/question/26865
#SPJ8
What's the answer? How do you get to the answer?

Answers
scale factor of triangle is 20/7 = 2.8571 .
How can I figure out the scale factor of a triangle?To get the scale factor of two triangles, follow these steps:
1. Check that the two triangles are similar.
2-If the triangles are similar, identify the sides that match.
3. Subtract any known angle from the triangle and multiply the result by the matching (also known) angle in the second triangle.
As a result,
4- the scale factor is equalized by the division.
CALCULATION∵ To find scale factor of two triangle we divide the sides of the both sides
∴ the scale factor of triangle given will be 20/7 = 2.8571 .
learn more about the scale factor here :
brainly.com/question/17202953
#SPJ9
If f(x) = 6x3 – 11x2
6x3 – 11x2 – 26x + 15 and
f(3) = 0, then find all of the zeros of f(x)
algebraically.
Answers
Answer:
f(6)g(8)f(3)=0
Step-by-step explanation:
its a mathematics formula its ia trick
Calculate each compound event probability: a. X ≤ 15, n = 20, π = .70 (Round your answer to 4 decimal places.) b. X > 8, n = 11, π = .65 (Round your answer to 4 decimal places.) c. X ≤ 1, n = 13, π = .40 (Round your answer to 4 decimal places.)
Answers
For X ≤ 15, n = 20, π = .70 ; compound event probability is approximately 0.0008 .
For X > 8, n = 11, π = .65 ; compound event probability is approximately 0.9198.
For X ≤ 1, n = 13, π = .40 ; compound event probability is approximately 0.6646 .
a. To calculate the probability of the event X ≤ 15, n = 20, π = .70, we will use the binomial distribution formula:
P(X ≤ 15)
= ∑_(k=0)¹⁵〖(20Ck)(0.70)^k (0.30)^(20-k) 〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.0008 (rounded to 4 decimal places).
b. To calculate the probability of the event X > 8, n = 11, π = .65, we will first find the probability of X ≤ 8, and then subtract this value from 1 to find the complement probability:
P(X > 8) = 1 - P(X ≤ 8)
= 1 - ∑_(k=0)⁸〖(11Ck)(0.65)^k (0.35)^(11-k)〗
Using a binomial distribution calculator, we can find the probability of X ≤ 8 to be approximately 0.0802.
Therefore, the probability of X > 8 is approximately 0.9198 (rounded to 4 decimal places).
c. To calculate the probability of the event X ≤ 1, n = 13, π = .40, we will use the binomial distribution formula:
P(X ≤ 1)
= ∑_(k=0)¹〖(13Ck)(0.40)^k (0.60)^(13-k)〗
Using a binomial distribution calculator, we can find this probability to be approximately 0.6646 (rounded to 4 decimal places).
For more such questions on event probability visit:
https://brainly.com/question/30390037
#SPJ8
In the following alphanumeric series, what letter comes next? V, Q, M, J, H, …

Answers
According to the given information, the letter that comes next in the given alphanumeric series is "N".
What is alphanumeric series?
An alphanumeric series is a sequence of letters and/or numbers that follows a certain pattern or rule. For example, "A, B, C, D, E..." is an example of an alphabetical series, and "1, 3, 5, 7, 9..." is an example of a numerical series. An alphanumeric series may combine both letters and numbers, such as "A1, B2, C3, D4, E5...". The pattern or rule followed by an alphanumeric series may be based on numerical or alphabetical order.
The given series V, Q, M, J, H, ... follows a pattern where each letter is the 6th letter from the previous letter. So, the next letter in the series would be 6 letters after H, which is N.
Therefore, the letter that comes next in the given alphanumeric series is "N".
To know more about the alphanumeric series visit:
brainly.com/question/10798102
#SPJ1
Evaluate 6x + 5y for x = 5 and y = 3.
Answers
Answer:
45
Step-by-step explanation:
Plug in the numbers with their variables.
6(5)+5(3)
30+15
45
Hope this helps
Plsssss help before it gets locked

Answers
B. Could be E or F
Answer:
uhhh i might be l;ate lol
Step-by-step explanation:
Mrs. Fisk, the art teacher, has 5 pounds of clay. Each of her students need 1/4 pound to complete their current project. How many students can she supply with clay?
Answers
Answer:
20 students
Step-by-step explanation:
solve simultaneously 2x - y = - 10 and 3x + 2y = - 1
Answers
The solution to the system of equations is x = -3 and y = -4.
To solve the system of equations:
Equation 1: 2x - y = -10
Equation 2: 3x + 2y = -1
We can use the method of substitution or elimination to find the values of x and y.
Let's use the method of elimination:
Multiply Equation 1 by 2 to make the coefficients of y in both equations equal:
2(2x - y) = 2(-10)
4x - 2y = -20
Now, we can eliminate y by adding Equation 2 and the modified Equation 1:
(3x + 2y) + (4x - 2y) = -1 + (-20)
7x = -21
x = -3
Substitute the value of x into Equation 1 to solve for y:
2(-3) - y = -10
-6 - y = -10
y = -10 + 6
y = -4
Therefore, the solution to the system of equations is x = -3 and y = -4.
for such more question on equations
https://brainly.com/question/17482667
#SPJ8
What is the sum of the roots of the equation

Answers
Answer:
-2.5
Step-by-step explanation:
For a quadratic equation \(ax^2 + bx+c=0\), the sum of the roots is \(-b/a\).
Here, \(b=5\) and \(a=2\), so the sum is \(-2.5\).
Help meeeeeeeeeeeeeeeeeeee

Answers
Answer:
I believe it is y=1x or y=x
Answer:
14
Step-by-step explanation:
The constant of proportionality is the y number when x is 1. Look on the bottom of the graph. Find 1, so up to the line and then across left to the y axis. you will be at 14. This means that every time the x increases by 1, the increases by 14
9)Rover the dog is on a 60-foot leash. One end of the leash is tied to Rover, who is 2 feet tall. The
other end of the leash is tied to the top of an 8-foot pole. How far can Rover roam from the
pole?
Answers
The dog can roam 59.7 feet if the dog is on a 60-foot leash. One end of the leash is tied to Rover, who is 2 feet tall.
What is the Pythagoras theorem?The square of the hypotenuse in a right-angled triangle is equal to the sum of the squares of the other two sides.
We have:
Rover the dog is on a 60-foot leash. One end of the leash is tied to Rover, who is 2 feet tall. The other end of the leash is tied to the top of an 8-foot pole.
After drawing a right-angle triangle from the above information.
Applying Pythagoras' theorem:
60² = 6² + x²
After solving:
x = 59.69 ≈ 59.7 foot
Thus, the dog can roam 59.7 feet if the dog is on a 60-foot leash. One end of the leash is tied to Rover, who is 2 feet tall.
Learn more about Pythagoras' theorem here:
https://brainly.com/question/21511305
#SPJ1

Jake drives a tractor from one town to another, a distance of 120 kilometers. He drives 6 kilometers per hour faster on the return trip, cutting 1 hour off the time. How fast does he drive each way?
Answers
The speed of Jake's initial trip is x = 24 kilometers per hour, and the speed of the return trip is x + 6 = 30 kilometers per hour.
Let's assume that Jake's speed during the initial trip is represented by "x" kilometers per hour.
On the return trip, he drives 6 kilometers per hour faster, so his speed can be represented as "x + 6" kilometers per hour.
To find the time taken for each trip, we can use the formula Time = Distance / Speed.
For the initial trip, the time taken is 120 kilometers divided by x kilometers per hour, which gives us 120/x hours.
On the return trip, the time taken is 120 kilometers divided by (x + 6) kilometers per hour, which gives us 120/(x + 6) hours.
According to the problem, the return trip takes 1 hour less than the initial trip. So we can set up the equation:
120/x - 1 = 120/(x + 6)
To solve this equation, we can multiply both sides by x(x + 6) to eliminate the denominators:
120(x + 6) - x(x + 6) = 120x
Simplifying this equation:
120x + 720 - x² - 6x = 120x
Combining like terms:
x² + 6x - 720 = 0
Now we can solve this quadratic equation by factoring or using the quadratic formula. By factoring, we find:
(x + 30)(x - 24) = 0
This gives us two potential solutions: x = -30 or x = 24.
Since speed cannot be negative, we discard the solution x = -30.
Therefore, the speed of Jake's initial trip is x = 24 kilometers per hour, and the speed of the return trip is x + 6 = 30 kilometers per hour.
So, Jake drives at a speed of 24 kilometers per hour on the initial trip and 30 kilometers per hour on the return trip.
For similar question on speed.
https://brainly.com/question/29483294
#SPJ8
Perform the indicated operation:
(4 + 2i) (1 + 5i)
-6 +22i
6-221
-14 + 18i
6+22i
Answers
Answer:
-235+84i
Step-by-step explanation:
I hope this is what you were looking for.
Which line is parallel to the line 8x + 2y = 12?
Help ASP please!!!

Answers
To be parallel must the slope of the lines equal to each other.
_________________________________
\(8x + 2y = 12\)
\(2y = - 8x + 12\)
\(y = - 4x + 6\)
_________________________________
From left to right ;
1) The slope-intercept form is :
\(y = 4x + 4\)
Which means the slope = 4
Look : 4 ≠ -4 thus this is not the answer.
+++++++++++++++++++++++++++++++++++++++
2) The slope-intercept form is :
\(y = - \frac{1}{4}x + \frac{3}{4} \\ \)
Which means the slope = -¼
Look : -¼ ≠ -4 thus this is not the answer.
+++++++++++++++++++++++++++++++++++++++
3) The slope-intercept form is :
\(y = - 4x - 6\)
Which means the slope = -4
Look : -4 = -4 thus this is the answer.
+++++++++++++++++++++++++++++++++++++++
4) The slope-intercept form is :
\(y = \frac{1}{4}x + \frac{11}{4}\\ \)
Which means slope = ¼
Look : ¼ ≠ -4 thus this is not the answer.
_________________________________
And we're done...
♥️♥️♥️♥️♥️
0.000549 in scientific notation
Answers
Answer: 5.49 × 10-4
Step-by-step explanation:
When you move the decimal over move it over to the right by 4 units.
When you move right it is (-) negative. So you get 5.49 x 10-4.
rancesca watched
1
4
of a movie in the morning, and she watched some more at night. By the end of the day, she still had
1
3
of the movie left to watch. How much of the movie did Francesca watch at night?
Answers
Answer:
-1/12 = -0.083
Step-by-step explanation:
Pleaseee helpp mee, I need an answer asap!!

Answers
Answer: 7 units
Step-by-step explanation:
Using the distance formula, the square root of (X2 - X1)^2 + (Y2 - Y1)^2 is equal to the distance between two points.
5-(-2) = 7 9^2 equals 49
-3-(-3) = 0
The square root of 49 plus 0 is 7, so the answer is 7 units.
What is the answer? Links will be reported. ( BRANLIEST )

Answers
Answer:
\( - 1 \frac{1}{8} m + \frac{3}{10} \\ \)
Step-by-step explanation:
\( \frac{7}{8} m + \frac{9}{10} - 2m - \frac{3}{5} \\ \frac{7}{8} m - 2m + \frac{9}{10} - \frac{3}{5} \\ \frac{7}{8} m - \frac{2m \times 8}{1 \times 8} + \frac{9}{10} - \frac{3 \times 2}{5 \times 2} \\ \frac{7m - 16m}{8} + \frac{9 - 6}{10} \\ - \frac{9}{8} m + \frac{3}{10} \\ - 1 \frac{1}{8} m + \frac{3}{10} \\ \)
the quotient of a number x and two tenths
Answers
The quotient of a number x and two tenths is 5x
What is quotient?Quotient is defined as the quantity derived from the division of two numbers.
From the information given, we are to find the the quotient of;
a number x two tenths represented as 2/ 10 = 0. 2The quotient is written thus;
= x/ 2/ 10
Take the inverse of the denominator and multiply
= x × 10/ 2
= 10x/ 2
find common divisor
= 5x
Thus, the quotient of a number x and two tenths is 5x
Learn more about quotient here:
https://brainly.com/question/629998
#SPJ1
Leah works at an appliance store. She recorded her recent sales.
washing machines 3
dishwashers 1
ovens 6
clothes dryers 5
What is the experimental probability that the next appliance Leah sells will be an oven?
Answers
6/15
you add everything she sells together. ( 3+1+6+5=15) Then you put the amount of ovens she sells above taht number, making it a fraction.
Find the values of x between 0 and pi where the tangent line to the graph of y = sin(x) cos(x) is horizontal.
Answers
Answer:
π/4, or 3π/4
Step-by-step explanation:
dy/dx = cos(x)*cos(x)+sin(x)*[-sin(x)]=(cosx)^2-(sinx)^2=[1-(sinx)^2]-(sinx)^2 = 1-2(sinx)^2
Tangent line is horizontal, so dy/dx = 0
1-2(sinx)^2 = 0
(sinx)^2 = 1/2
sinx = \(\frac{1}{\sqrt{2}}, -\frac{1}{\sqrt{2}}\)
Between 0 and pi, sinx >0
so sinx = \(\frac{1}{\sqrt{2}}\)
x = π/4, or 3π/4
which is greater 4 4/10 or 32/10
Answers
44/10 > 32/10
Answer:
4 4/10 is greater.
Step-by-step explanation:
4 = 40/10
then:
4 4/10 = 4 + 4/10 = 40/10 + 4/10 = (40+4)/10 = 44/10
Then:
44 > 32
44 is greater.
math question pls help asap thxxu
question is in pic

Answers
Step-by-step explanation:
you use a cah method which mean to get the angle you divide the adjacent length by hypotenuse and then find the CAH inverse using your calculator to get the angle
2 miles
Find x.
X
3 miles
x = √[?] miles
![2 milesFind x.X3 milesx = [?] miles](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/MDuzRtfLbHl5AHRnWC5zNzx79RCH1Lgi.png)
Answers
The value of x is √3 miles
How to determine the valuesTo determine the value of the variable, we need to know the Pythagorean theorem.
The Pythagorean theorem states that the square of the longest leg of a triangle is the sum of the squares of the other two sides of that triangle
From the information given, we have that;
The longest leg = x
The value of the opposite = 2 miles
The value of the adjacent = 3 miles
then, we have that;
x² = 2² + 3²
Find the value of the square
x² = 4 + 9
Add the values
x² = 13
Find the square root of both sides
x = √13 miles
Learn more about Pythagorean theorem at: https://brainly.com/question/654982
#SPJ1
A relation is shown (2,7), (0.1), (8, 9), (12, 18), (?, ?)} Select all ordered pairs that could replace the missing ordered pair to make the relation a function. •(-2,9)•(8,-18)•(7,-2)•(-8,0)•(0,0)
Answers
In order to be a function, the input values (x) must have only one output value (y)
So:
Possible pairs.
(-2,9)
(7,-2)
(-8,0)
Help me find one possible solution to the inequality and show how it makes sense in the situation.
A yearbook company promises to give the junior class a picnic if they spend at least $28,000 on yearbooks and class rings. Each yearbook costs $35, and each class ring costs $140. How many yearbooks and class rings must the junior class buy to get their picnic?
here is the inequality: 35x + 140y ≥ 2800
Answers
Answer:
A - 200.
B - 1 Class Ring and 796 yearbooks.
C - No, they would come up short 2800 dollars.
Find the missing values of the variables. The diagram is not to scale.
125°
yº
124/xº
65°
a. x = 124, y
= 125
b. x 56, y 114
C. X =
114, y = 56
d. X =
56,y
= 124
e. X = 56,y
= 125

Answers
Answer:
b. x = 56; y = 114
Step-by-step explanation:
✅124° + x° = 180° (linear pair/angles on a straight line)
Subtract 124° from each side
124° + x - 124° = 180° - 124°
x = 56°
✅x + y + 125° + 65° = 360° (sum of interior angles of a quadrilateral)
plug in the value of x
56 + y + 125 + 65 = 360
246 + y = 360
Subtract 246 from each side
246 + y - 246 = 360 - 246
y = 114°
-1/2+3/4
ASAP
Please helppppppp
Answers
Answer:
1/4
Step-by-step explanation:
-1/2 + 3/4
-1(2)/2(2) + 3/4
-2/4 +3/4
-2+3= 1
so 1/4