I can use reasoning to estimate decimal quotients. O A. strongly agree o O B. agree o C. disagree D. strongly disagree
Answers
Answer:
O A. strongly agree
Step-by-step explanation:
mark me brainliest!
Related Questions
7.) Use the Pythagorean Theorem to determine the length between points Q and P.
J

Answers
Answer:
14
Step-by-step explanation:
got it right
Divide f(x) by d(x). Your answer
should be in the following format:
f(x)
d(x)
f(x)
d(x)
Q(x) +
=
4x³8x²+2x1
2x + 1
[?]
R(x) = -²
R(x)
d(x)

Answers
The value of R(x) is - [1-7x]
What is division in algebra?
The four basic arithmetic operations of addition, subtraction, multiplication, and division are used to connect variables and constants in algebraic expressions. The procedure of multiplying and dividing algebraic expressions is the opposite of each other. You can divide algebraic expressions using the long division method, the division of a monomial by another monomial, or the division of a polynomial by another polynomial.
Dividend: The number or value that we divide is known as a dividend.
Divisor: The number that divides the dividend is known as a divisor
Quotient: The result obtained from the division process is known as a quotient
Remainder: The number left over after the division process is known as the remainder.
In the given question;
f(x) is dividend and
d(x) is divisor
Q(x) is the quotient
And we have to find the remainder i.e. R(x)
After dividing \(\frac{4x^3-8x^2+2x-1}{2x+1}\) we get
Q(x) =\(2x^2-5x\)
and R(x) = \(-[1-7x]\)
Learn more about Division in algebra from the link below
https://brainly.com/question/25289437
#SPJ1

Answer: 9/2
Step-by-step explanation:
Solve 2-3 cos x=5+3 cosx for 0° ≤ 180°
Answers
The equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
1. Start with the given equation: 2-3cos(x) = 5+3cos(x).
2. Subtract 3cos(x) from both sides to isolate the constant term: 2-3cos(x) - 3cos(x) = 5.
3. Combine like terms: 2-6cos(x) = 5.
4. Subtract 2 from both sides: -6cos(x) = 3.
5. Divide both sides by -6: cos(x) = -1/2.
6. To find the solutions for cos(x) = -1/2 in the range of 0° to 180°, we need to determine the angles where cos(x) equals -1/2.
7. These angles are 120° and 240°, as cos(120°) = cos(240°) = -1/2.
8. However, the given equation states that 2-3cos(x) equals 5+3cos(x), which is not satisfied by cos(x) = -1/2.
9. Therefore, the equation 2-3cos(x) = 5+3cos(x) has no solution in the range of 0° to 180°.
For more such questions on equation, click on:
https://brainly.com/question/17145398
#SPJ8
The last traffic light before Maud gets home has a 44% chance of being green when she reaches it. Let I
be the number of times Maud reaches the traffic light before she has to stop at it. Assume that each time is
independent of the others.
Find the mean and standard deviation of T.
Round your answers to one decimal place.
Answers
Answer:
Mean = 1.8 times
Standard Deviation = 1.2 Times
Step-by-step explanation:
Determine the period of the function f(t) 2.3cos0.25t
a period .25pi
b period 2pi
c period .5pi
d period 8pi
Answers
The period of the function f(t) = 2.3cos(0.25t) is 8π. Hence, the correct answer is d) period 8π.
To determine the period of the function f(t) = 2.3cos(0.25t), we need to consider the coefficient of t inside the cosine function.
In this case, the coefficient is 0.25, which represents the frequency of the cosine function. The period of a cosine function is given by the formula T = 2π/frequency.
Using this formula, we can calculate the period of the function f(t) as follows
T = 2π / 0.25
T = 8π
Therefore, the period of the function f(t) = 2.3cos(0.25t) is 8π.
Hence, the correct answer is d) period 8π.
The period of a function represents the length of one complete cycle or the distance between two consecutive identical points on the graph of the function. In this case, the function is a cosine function, and the period determines how long it takes for the function to repeat its values
The coefficient 0.25 in the function f(t) = 2.3cos(0.25t) affects the frequency of the cosine function. A smaller coefficient results in a slower oscillation, while a larger coefficient leads to a faster oscillation. In this case, since the coefficient is 0.25, it means that the function completes one full cycle within 8π units of time.
Understanding the period of a function is crucial for analyzing its behavior, identifying the frequency of oscillation, and studying its repetitive patterns.
for more such question on function visit
https://brainly.com/question/11624077
#SPJ8
How is 9/12 equivalent to 4/6
Answers
Answer:
it's not
Step-by-step explanation:
if you simplify by making the denominators the same (multiplying 9/12 by 6/6 and 4/6 by 12/12), you'll arrive at 54/72 and 48/78. 54 isn't equal to 48
Can someone please help me

Answers
f(x)= - 1/3 + 13
when the x- value is ( -3)
Answers
I'm going to assume the "x" goes after "-1/3"
f(-3) = -1/3(-3) + 13
f(-3) = 1 + 13
f(-3) = 14
Best of Luck!
Suppose you do not know the population mean fee charged to H&R Block customers last year. Instead, suppose you take a sample of size n-8 and find a sample mean of 350. Assume that the distribution for fees is normally distributed with a sample standard deviation of $100.
i. Before conducting the survey, suppose you believed based on your previous observations, your best guess for population standard deviation of fee charged to H&R Block is $50. With this assumption in mind, What should your sample size n approximately be if you want:
Margin-of-Error of to be 2 % and confidence level to be 95 %?
Margin-of-Error of to be 4% and confidence level to be 95%?
Margin-of-Error of to be 4 % and confidence level to be 99%?
ii. 90% confidence interval for the population mean of fees H&R Block.
a. Calculate the margin of error (MOE) of x using a 10% significance level.
b. Calculate the 90 % confidence interval.
c. Suppose an analyst belief that the population mean fee is equal to $185. Using a 90% confidence level. can we conclude the analyst is right? Why or why not?
Answers
Answer:
i \(\to\) a
\(n = 96040000\)
i \(\to\) b
\(n_1 =24010000\)
i \(\to\) c
\(n_2 =41602500\)
ii\(\to\)a
\(E = 58.16\)
ii\(\to\)b
\(291.84 < \mu < 408.16\)\
ii\(\to\)c
There is insufficient evidence to conclude that the analyst is right because the population mean fee by the analyst does not fall within the confidence interval
Step-by-step explanation:
From the question we are told that
The sample size is \(n = 8\)
The sample mean is \(\= x = \$ 350\)
The sample standard deviation is \(\$ 100\)
Considering question i
i \(\to\) a
At \(E = 0.02\)
given that the confidence level is 95% = 0.95
the level of significance would be \(\alpha =1-0.95 = 0.05\)
The critical value of \(\frac{\alpha }{2}\) from the normal distribution table is
\(Z_{\frac{ \alpha }{2} } = 1.96\)
So the sample size is mathematically evaluated as
\(n = [ \frac{Z_{\frac{\alpha }{2} } * \sigma }{E} ]^2\)
=> \(n =[ \frac{ 1.96 * 100}{ 0.02} ]^2\)
=> \(n = 96040000\)
i \(\to\) b
At \(E_1 = 0.04\) and confidence level = 95% => \(\alpha_1 = 0.05\) => \(Z_{\frac{\alpha_1 }{2} } = 1.96\)
\(n_1 = [ \frac{Z_{\frac{\alpha_2 }{2} } * \sigma }{E_1} ]^2\)
=> \(n_1 =[ \frac{ 1.96 * 100}{ 0.04} ]^2\)
=> \(n_1 =24010000\)
i \(\to\) c
At \(E_2 = 0.04\) confidence level = 99% => \(\alpha_2 = 0.01\)
The critical value of \(\frac{\alpha_2 }{2}\) from the normal distribution table is
\(Z_{\frac{ \alpha_2 }{2} } = 2.58\)
=> \(n_2 = [ \frac{Z_{\frac{\alpha_2 }{2} } * \sigma }{E_2} ]^2\)
=> \(n_2 =[ \frac{ 2.58 * 100}{ 0.04} ]^2\)
=> \(n_2 =41602500\)
Considering ii
Given that the level of significance is \(\alpha = 0.10\)
Then the critical value of \(\frac{\alpha }{2}\) from the normal distribution table is
\(Z_{\frac{\alpha }{2} } = 1.645\)
Generally the margin of error is mathematically represented as
\(E = Z_{\frac{\alpha }{2} } * \frac{\sigma }{\sqrt{n} }\)
substituting values
\(E = 1.645 * \frac{100 }{\sqrt{8} }\)
\(E = 58.16\)
Generally the 90% confidence interval is mathematically evaluated as
\(\= x - E < \mu < \= x + E\)
=> \(350 - 58.16 < \mu < 350 + 58.16\)
=> \(291.84 < \mu < 408.16\)
So the interpretation is that there is 90% confidence that the mean fee charged to H&R Block customers last year is in the interval .So there is insufficient evidence to conclude that the analyst is right because the population mean fee by the analyst does not fall within the confidence interval.
Simplify 3(x+2) + 2x + 5
Answers
Answer:
\(5x+11\)
Step-by-step explanation:
Step 1: Distribute
\(3x+6+2x+5\)
Step 2: Add like terms
\(5x+11\) < your answer
simplify; 8/15 + 1/6
A 1/10
B 7/30
C 11/30
D 7/10
Answers
Answer:
7/10
Step-by-step explanation:
Answer:
The choice D.
\( \frac{7}{10} \)
Step-by-step explanation:
\( \frac{8}{15} + \frac{1}{6} \\ \\ \frac{48}{90} + \frac{15}{90} = \frac{63}{90} \\ \\ \frac{63 \div 9}{90 \div 9} = \frac{7}{10} \)
You are selling flowers for a school fundraiser. When you purchase them, roses cost $3.50 and daisies cost $1.25. You have $300 to purchase flowers.
You sell 150 flowers total.
Answers
Answer:
So, if we sell 150 flowers total, we can purchase 100 daisies and 50 roses for exactly $300.
Step-by-step explanation:
Let R be the number of roses and D be the number of daisies.
Now we can set the following equations to represent the cost and the total number of flowers,
Cost equation=3.50R + 1.25D
= 300
Number of flowers equation= R + D
= 150
We need to find the number of roses and daisies that we can purchase, as according to question the total number of flowers is 150. To find R, we can put value of the number of flowers in the equation for R in terms of D, and also put this expression for R in the cost equation,
R = 150 - D
3.50R + 1.25D
= 300
3.50(150 - D) + 1.25D
= 300
525 - 3.50D + 1.25D
= 300
-2.25D = -225
D = 100
Therefore, we can buy 100 daisies and the remaining 50 flowers must be roses.
The cost of 100 daisies is 100 × 1.25
= $125
The cost of 50 roses is 50 × 3.50
= $175.
Therefore, the total cost is $125 + $175
= $300.
So, if we sell 150 flowers total, we can purchase 100 daisies and 50 roses for exactly $300.
A 0.60-kg basketball is dropped out of a window that is 6.1mabove the ground. The ball is caught by a person whose handsare 1.5m above the gound.1. How much work is done on e the ball by its weight?What is the gravitational potential energy of the basketball,relative to the ground, when it is ... 2. released and 3. caught?4. How is the change (PEf- PE0) in the ball'sgravitational potential energy related to the workdone by its weight?
Answers
The work that gravity does;
W = F.S = mgΔh
In light of the fact that gravity points downward and that displacement is also downward, their angle is 0 and their cosine 1, respectively.
W = mgΔh
g = 9.8 m/s²
Δh = 4.6 m
m = 0.60 kg
W = 0.60 x 9.80 x 4.6
W = 2.7 J
The source of gravitational potential energy in relation to the ground is;
U = mgh
The release point therefore
Ug = mgh(0)
U0 = 0.60 x 9.8 x 6.1
U0 = 35.87 J
At the point of release
U(gf) = mgh(f)
U(gf) = 0.60 x 9.80 x 1.5
U(gf) = 8.820 J
Gravitational potential energy changes are;
ΔU(g) = U(gf) - U0
ΔU(g) = 8.820 J - 35.87 J
ΔU(g) = -27.05 J
Result, we can see that the work done through gravity is the opposite of how the gravitational potential energy has changed.
To know more about the gravitational potential energy, here
https://brainly.com/question/3120930
#SPJ4

Solve for y. 2(y-2) -6y=-28
Answers
Answer:
y = -8
Step-by-step explanation:
2(y-2)- 6y-28 = 0
2y - 4 -6y - 28 = 0
-4y = 32
y = -8
Find the surface area of a rectangular solid with the given dimensions length 28 feet, width 25 feet, height 24 feet. give your answer without units
Answers
Surface area of the solid = 3944
Explanation:The shape is said to be a rectangular solid. It could be a prism, box, etc
Surface area of rectanular prsim = 2(lh + wh + lw)
length = 28 ft
width = 25 ft
height = 24 ft
Surface area of the solid = 2(28 × 24 + 25 × 24 + 28 × 25)
Surface area of the solid = 2(1972)
Surface area of the solid = 3944
What is the data correlation in the scatter plot below?
No correlation
Positive
Negative

Answers
The data correlation in the scatter plot above include the following: B. positive.
What is a positive correlation?In Mathematics, a positive correlation is used to described a scenario in which two variables move in the same direction and are in tandem.
This ultimately implies that, a positive correlation exist when two variables have a linear relationship or are in direct proportion. Therefore, when one variable increases, the other variable generally increases, as well.
By critically observing the scatter plot shown in the image attached above, we can reasonably infer and logically deduce that there is a positive correlation between the x-values and y-values because they both increase simultaneously.
Read more on positive correlation here: brainly.com/question/3753830
#SPJ1
help quick due in 10 minutes you will be reported if you spam Ivan is 75 inches tall if his brother Logan was 5 inches shorter, he would be exactly half Evan's height How tall is Logan? Enter your answer as a decimal in the box,
Answers
Answer:
35
Step-by-step explanation:
if not correct I'm very very sorry I tried my best for this</3
please help please...

Answers
The required coordinate of B' is B' = (4, -5), across the y-axis after reflection. Option A is correct.
What is the transformation of geometry over the coordinate plane?Transform the shapes on a coordinate plane by rotating, reflecting, or translating them.
here,
Given that a point B (-4, -5) is reflected across the y-axis, the Coordinate of image B' is to be determined.
Since the coordinate is reflected across the y-axis,
The equation of trasformation is given as,
(x , y) ⇒ (-x , y)
So, the image of B,
B' = (-(-4), -5)
B' = (4, -5)
Thus, the required coordinate of B' is B' = (4, -5), across the y-axis after reflection. Option A is correct.
Learn more about transformation here: https://brainly.com/question/18065245
#SPJ1
A 2-column table with 4 rows. Column 1 is labeled x with entries 1, 2, 3, 4. Column 2 is labeled y with entries 11, 22, 33, 44. What relationship between the quantities is shown in the table? The relationship between quantities is +10. The relationship between quantities is ×11. The relationship between quantities is – 30. The relationship between quantities is + 20. A 2-column table with 4 rows. Column 1 is labeled x with entries 1, 2, 3, 4. Column 2 is labeled y with entries 11, 22, 33, 44. What relationship between the quantities is shown in the table? The relationship between quantities is +10. The relationship between quantities is ×11. The relationship between quantities is – 30. The relationship between quantities is + 20. A 2-column table with 4 rows. Column 1 is labeled x with entries 1, 2, 3, 4. Column 2 is labeled y with entries 11, 22, 33, 44. What relationship between the quantities is shown in the table? The relationship between quantities is +10. The relationship between quantities is ×11. The relationship between quantities is – 30. The relationship between quantities is + 20. A 2-column table with 4 rows. Column 1 is labeled x with entries 1, 2, 3, 4. Column 2 is labeled y with entries 11, 22, 33, 44. What relationship between the quantities is shown in the table? The relationship between quantities is +10. The relationship between quantities is ×11. The relationship between quantities is – 30. The relationship between quantities is + 20.
Answers
The relationship between the quantities shown in the table is +10. The values in column 2 (y) are obtained by adding 10 to the corresponding values in column 1 (x).
How to explain the relationshipIn the given table, the values in column 1 (labeled "x") are 1, 2, 3, and 4. The values in column 2 (labeled "y") are 11, 22, 33, and 44.
To determine the relationship between the quantities in the table, we can compare the values in column 2 (y) with the corresponding values in column 1 (x).
If we subtract each value in column 1 from the corresponding value in column 2, we find that:
11 - 1 = 10
22 - 2 = 20
33 - 3 = 30
44 - 4 = 40
By observing these results, we can see that the difference between each value in column 2 and its corresponding value in column 1 is always 10.
Learn more about table on
https://brainly.com/question/12151322
#SPJ1
Suppose that the volume of a right circular cylinder is 500 A cubic
centimeters and the radius of its base is 5 centimeters. What is the
height of the cylinder?
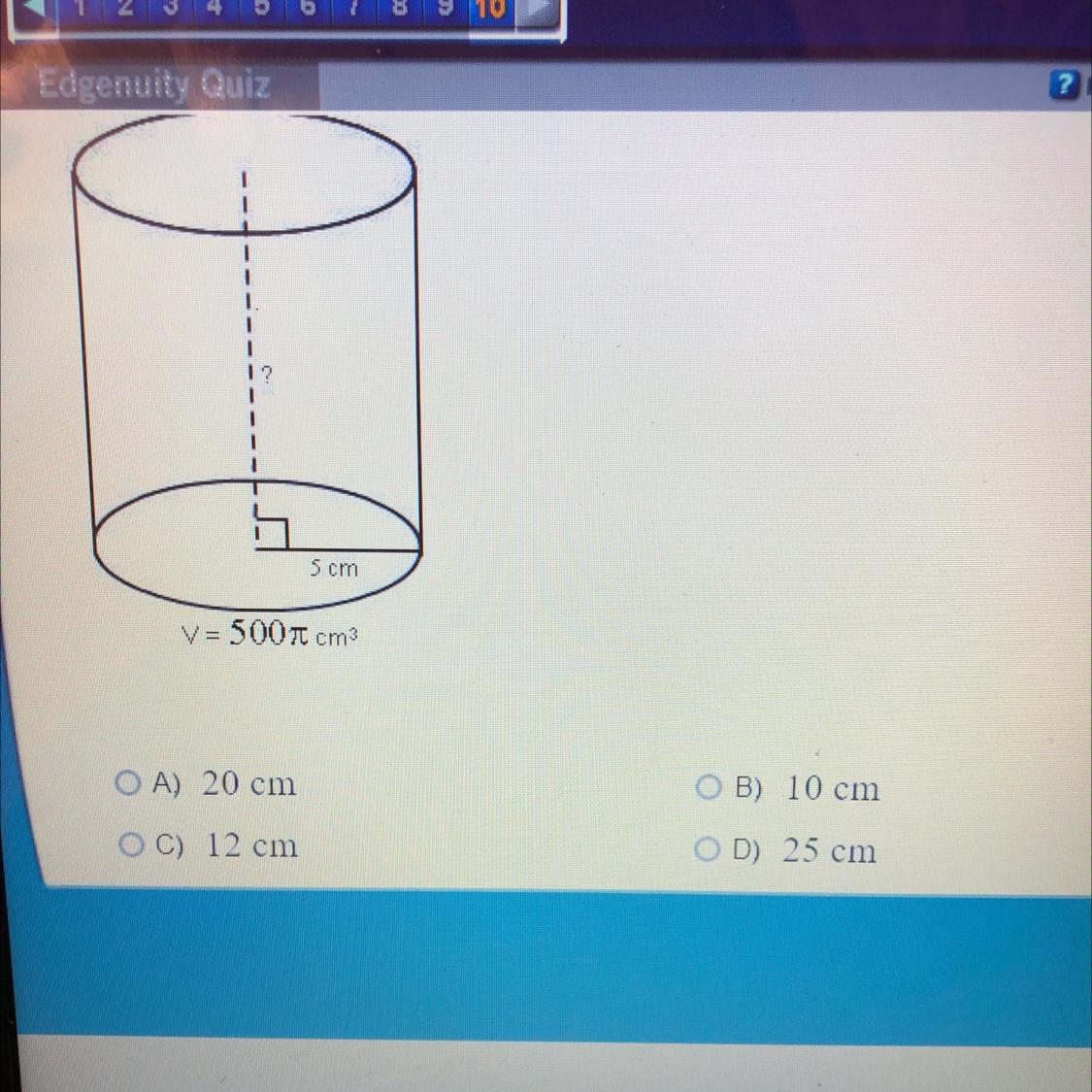
Answers
The height of the right circular cylinder with volume of 500π cubic centimetre and radius of 5 centimetre is 20 cm.
Volume of a cylindervolume = πr²h
where
r = radiush = heightTherefore,
volume = 500π cm³
r = 5 cm
Therefore,
volume of the cylinder = πr²h
500π = 5²πh
500π = 25πh
divide both sides by 25π
500π / 25π = 25πh / 25π
h = 20 cm
learn more on cylinder here: https://brainly.com/question/11083770
Answer:
A) 20 cm
Step-by-step explanation:
what divided by 2 equals 6.5
Answers
Answer:
hope this helps, take care and stay safe
Step-by-step explanation:
you can do this by timing 6.5 by 2 which = 13. if you get stuck on questions like this, do the rewind effect, that is when you do the opposite of the question, which is what i did above, you can check this in 2 ways, on a calculator (if of course you are allow) or do the question again by using what you have work out, so 13 divide by 2 = 6.5.
The number 13 is divided by 2 to give the number 6.5.
Used the concept of divide which states that,
The division method is used to distribute a group of things into equal parts. The division is just the opposite of multiplications.
To find the number that is divided by 2 to give the number 6.5
Let us assume that the number = x
Hence, it can be written as,
x ÷ 2 = 6.5
x/2 = 6.5
Multiply both sides 2;
x = 2 × 6.5
x = 13
Therefore, the number of the given condition is 13.
To learn more about the divide visit:
https://brainly.com/question/28119824
#SPJ6
B
a
A
b
Find the missing side c if Angle B -45 and side a=13
Round your answer to the nearest hundredth if necessary.

Answers

AB and BC are perpendicular lines find the value of x.
Answers
The equation is written as x + 25° + 25° = 90°. Then the value of the variable 'x' is 40°.
What is an angle?The inclination is the separation seen between planes or vectors that meet. Degrees are another way to indicate the slope. For a full rotation, the angle is 360°.
Adjacent angle - In math, two points are nearby in the event that they have a typical side and a typical vertex.
AB and BC are perpendicular lines. Then the equation is given as,
x + 25° + 25° = 90°
x + 50° = 90°
x = 90° - 50°
x = 40°
The equation is written as x + 25° + 25° = 90°. Then the value of the variable 'x' is 40°.
More about the angled link is given below.
https://brainly.com/question/15767203
#SPJ1
The complete question is given below.

Solve for x
(2^2/x) (2^4/x) = 2^12

Answers
\( \textsf{\qquad\qquad\huge\underline{{\sf Answer}}} \)
Let's solve ~
\(\qquad \sf \dashrightarrow \:(2 {}^{ \frac{2}{x} } ) \sdot(2 {}^{ \frac{4}{x} } ) = 2 {}^{12} \)
\(\qquad \sf \dashrightarrow \:(2 {}^{ \frac{2}{x} + \frac{4}{x} } ) = 2 {}^{12} \)
\(\qquad \sf \dashrightarrow \:(2 {}^{ \frac{6}{x} } ) = 2 {}^{12} \)
Now, since the base on both sides are equal, therefore their exponents are equal as well ~
\(\qquad \sf \dashrightarrow \: \dfrac{6}{x} = 12\)
\(\qquad \sf \dashrightarrow \:x = \dfrac{6}{12} \)
\(\qquad \sf \dashrightarrow \:x = \dfrac{1}{2} \)
or
\(\qquad \sf \dashrightarrow \:x = 0.5\)
Hope you got the required Answer ~
A diphosphonate kit contian 180 mCi of Tc99m in 30 ml when it is prepared at 8am. Immediately, a 20 mCi dose is withdrawn for a bone scan. if the patient arrives late at 9:30 and half the volume is accidentally discharged, how much volume from the kit must now be added to the syringe to correct the dose to 20 mCi? (no other doses have been withdrawn meanwhile, and the decay factor for 1.5 hrs is 0.841)
Answers
The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
To solve this problem, we can use the concept of radioactive decay and the decay factor. Here's how we can calculate the required volume to correct the dose:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = Initial activity * Decay factor
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = Initial activity - 20 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = Remaining activity * Decay factor
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = Desired activity at 9:30 / Remaining activity at 9:30 * Volume at 9:30
Calculate the remaining volume at 9:30:
Remaining volume = Volume at 8 am - Volume withdrawn - Volume accidentally discharged
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume
Let's perform the calculations step by step:
Determine the initial activity of the kit:
Initial activity = 180 mCi
Calculate the decayed activity at 9:30 (after 1.5 hours):
Decay factor = 0.841
Decay activity = 180 mCi * 0.841 = 151.38 mCi
Calculate the remaining activity after withdrawing 20 mCi at 8 am:
Remaining activity = 180 mCi - 20 mCi = 160 mCi
Calculate the remaining activity at 9:30:
Remaining activity at 9:30 = 160 mCi * 0.841 = 134.56 mCi
Calculate the desired activity at 9:30 (20 mCi):
Desired activity at 9:30 = 20 mCi
Calculate the volume needed to achieve the desired activity:
Volume needed = (Desired activity at 9:30 / Remaining activity at 9:30) * Volume at 9:30
Volume at 9:30 = Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Volume needed = (20 mCi / 134.56 mCi) * 15 ml = 2.236 ml
Calculate the remaining volume at 9:30:
Remaining volume = 30 ml - (30 ml / 2) = 15 ml
Calculate the volume that needs to be added:
Volume to be added = Volume needed - Remaining volume = 2.236 ml - 15 ml = -12.764 ml
Since the calculated volume to be added is negative, it means that no additional volume is required. The remaining Kit volume in the syringe is sufficient to correct the dose to 20 mCi.
For such more questions on Kit Volume Correction
https://brainly.com/question/22971212
#SPJ8
Analysis of daily output of a factory shows that, on average, the number of units per hour y produced after t hours of production is
y = 102t + 0.5t2 − t3, 0 ≤ t ≤ 10.
(a) Find the critical values of this function. (Assume −[infinity] < t < [infinity]. Enter your answers as a comma-separated list.)
t =
(b) Which critical values make sense in this particular problem? (Enter your answers as a comma-separated list.)
(c) For which values of t, for 0 ≤ t ≤ 10, is y increasing? (Enter your answer using interval notation.)
Answers
The critical values for the function are t = 6 , -5.667 where t = 6 makes sense . At t = 6 , y is increasing
According to the question,
After t hours of production, a plant produces an average of y units per hour, according to analysis of its daily output is
y = 102t + 0.5t² - t³ , 0 ≤ t ≤ 10
(a) To calculate critical values for the given function
We have to differentiate it w.r.t time and then have to put y'=0
=> y = 102t + 0.5t² - t³
Derivating w.r.t time
=> y' = 102 + t - 3t²
Equating to zero,
=> 102 + t - 3t² = 0
Solving quadratic equation,
=> t = 6 , -5.667 are critical values
(b) t = 6 makes sense in particular problem because time cannot be negative.
(c) To check increasing value
Derivate y' w.r.t time again
=> y" = 1 - 6t
Putting critical value,
At t = 6
y" < 0 , Therefore at t = 6 function is increasing
Hence , For t = 6 y is increasing
To know more about Critical value here
https://brainly.com/question/29095707
#SPJ4
A customer spends a total of $52.25 at an amusement park. The customer buys a $30.25 ticket to enter the park and 4 game tickets.
If each game ticket costs the same amount, x, which statement is true?
Responses
An equation that can be used to find x is 4(x+30.25)=52.25, and each game ticket costs $5.50.
An equation that can be used to find x is 4 ( x + 30.25 ) = 52.25 , and each game ticket costs $ $ 5.50 .
An equation that can be used to find x is 4(x+30.25)=52.25, and each game ticket costs $18.00.
An equation that can be used to find x is 4 ( x + 30.25 ) = 52.25 , and each game ticket costs $ $ 18.00 .
An equation that can be used to find x is 4x+30.25=52.25, and each game ticket costs $5.50.
An equation that can be used to find x is 4 x + 30.25 = 52.25 , and each game ticket costs $ $ 5.50 .
An equation that can be used to find x is 4x+30.25=52.25, and each game ticket costs $18.00.
Answers
Answer: I believe its: An equation that can be used to find x is 4x+30.25=52.25, and each game ticket costs $5.50.
Step-by-step explanation:
well, 52.25 - 30.25 is 22$
22 divided by 4 is 5.50
4 times x plus 30.25 is 52.25
so 4x+30.25= 52.25
Suppose an annuity pays 4% annual interest, compounded annually. If you invest $4,500 in this annuity annually for 10 years, what percentage of the total balance is interest earned? Round your answer to the nearest hundredth of a percent. Do NOT round until you have calculated the final answer.
Answers
\(~~~~~~~~~~~~\stackrel{\textit{payments at the beginning of the period}}{\textit{Future Value of an annuity due}} \\\\ A=pmt\left[ \cfrac{\left( 1+\frac{r}{n} \right)^{nt}-1}{\frac{r}{n}} \right]\left(1+\frac{r}{n}\right)\)
\(\qquad \begin{cases} A=\textit{accumulated amount} \\ pmt=\textit{periodic payments}\dotfill & 4500\\ r=rate\to 4\%\to \frac{4}{100}\dotfill &0.04\\ n= \begin{array}{llll} \textit{times it compounds per year}\\ \textit{annually, thus once} \end{array}\dotfill &1\\ t=years\dotfill &10 \end{cases}\)
\(A=4500\left[ \cfrac{\left( 1+\frac{0.04}{1} \right)^{1 \cdot 10}-1}{\frac{0.04}{1}} \right]\left(1+\frac{0.04}{1}\right) \\\\\\ A=4500\left[ \cfrac{(1.04)^{10}-1}{0.04} \right](1.04) \implies A \approx 56188.58\)
so every year you were putting in 4500 bucks, so for 10 years that'd be a total deposits for 4500*10 = 45000, so let's squeeze out the 45000 from the the total, that gives us 56188.58 - 45000 ≈ 11188.58.
so, if we take 56188.58 to be the 100%, what's 11188.58 off of it in percentage?
\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 56188.58 & 100\\ 11188.58& x \end{array} \implies \cfrac{56188.58}{11188.58}~~=~~\cfrac{100}{x} \implies 56188.58x=1118858 \\\\\\ x=\cfrac{1118858}{56188.58}\implies x\approx \stackrel{\%}{19.91}\)
please fast if could

Answers
Answer:9/41
SOH = opposite over hypotenuse
Step-by-step explanation:
What is the value of the expression -3(3+2)
Answers
Answer:
-15
Step-by-step explanation: