Answers
Answer:
(0, ∞)
Step-by-step explanation:
A good place to start is by visualizing what the graph looks like on a number line.
For x > 0, it is an open circle at x=0, and shading to the right extending to infinity.
__
So, the left end of the interval is 0, but 0 is not included in the interval.
The right end of the interval is infinity, but there is no such number, so "infinity" is not included in the interval.
"Not included" means you use round brackets ( ) for the corresponding end of the interval. ("Included" would mean you use square brackets [ ].)
So, the interval 0 < x < ∞ is written in interval notation as ...
(0, ∞)
Related Questions
if h(x)=(f o g)(x) and h(x)=\sqrt[4]{x+7} find g(x) if f(x)= \sqrt[4]{x+1}
Answers
The function g(x), considering that h(x) is the composite function of f(x) and g(x), is given as follows:
g(x) = x + 6.
What is the composite function of f(x) and g(x)?The composite function of f(x) and g(x) is given by the following rule:
h(x) = (f ∘ g)(x) = f(g(x)).
It means that the output of the inside function serves as the input for the outside function.
The functions for this problem are defined as follows:
\(h(x) = \sqrt[4]{x + 7}\)\(f(x) = \sqrt[4]{x + 1}\)Hence the function g(x) is defined as follows:
g(x) = x + 6.
As the application of the composite function is given as follows:
\(h(x) = (f \circ g)(x) = f(x + 6) = \sqrt[4]{x + 6 + 1} = \sqrt[4]{x + 7}\)
More can be learned about composite functions at https://brainly.com/question/10687170
#SPJ1
The measures of the angles of △ABC are given by the expressions in the table.

Answers
The angles of the triangle are 125 degrees, 20 degrees, and 35 degrees.
Define triangles.A triangle is a closed geometric shape with three sides, three angles, and three line segments. Three non-collinear points are joined by line segments to create the simplest polygon, which has three non-collinear points.
Triangles can be categorized according to the size of their sides and angles. Triangles can be categorized as equilateral (all sides are equal in length), isosceles (both sides are equal in length), or scalene based on their sides (all sides are different in length). Triangles can be categorized as acute (all angles are less than 90 degrees), obtuse (one angle is greater than 90 degrees), or right (one angle is greater than 90 degrees) (one angle is exactly 90 degrees).
In any triangle, the sum of the three interior angles is always 180 degrees. Therefore, we can write:
a + b + c = 180
Substituting the given values, we get:
(6x-1) + 20 + (x+14) = 180
Simplifying and solving for x, we get:
7x + 33 = 180
7x = 147
x = 21
Now that we have the value of x, we can substitute it back into the expressions for the angles to find their values:
angle a = (6x-1) = (6*21-1) = 125 degrees
angle b = 20 degrees
angle c = (x+14) = (21+14) = 35 degrees
Therefore, the angles of the triangle are 125 degrees, 20 degrees, and 35 degrees.
To know more about triangles, visit:
https://brainly.com/question/17335144
#SPJ1
A group of 8 friends went to lunch and spent a total of $76, which included the food bill and a tip of $16. They decided to split the bill and tip evenly among themselves. Which equations and solutions describe the situation? Select two options. The equation StartFraction 1 over 8 EndFraction (x + 16) = StartFraction 76 over 8 EndFraction represents the situation, where x is the food bill. The equation StartFraction 1 over 8 EndFraction (x + 16) = 76 represents the situation, where x is the food bill. The solution x = 60 represents the total food bill. The solution x = 60 represents each friend’s share of the food bill and tip. The equation 8 (x + 16) = 76 represents the situation, where x is the food bill.
YALL PLEASE HELP ASAP
Answers
Answer:
The solution x = 5 represents each friend's share of the food bill and tip.
RATE 5 stars and mark brainliest
A barn contains 11 animals. 7 of the animals are bats and the rest are mice. An animal leaves the barn at random, and then a second animal leaves th at random. Copy and complete the tree diagram, which shows all the possible outcor What is the probability that a mouse leaves first and then a bat? Give your answer as a fraction in its simplest form.
Answers
The probability that a mouse leaves first and then a bat is given as follows:
14/55.
How to calculate a probability?The parameters that are needed to calculate a probability are listed as follows:
Number of desired outcomes in the context of a problem or experiment.Number of total outcomes in the context of a problem or experiment.Then the probability is calculated as the division of the number of desired outcomes by the number of total outcomes.
As the animal is not replaced, the probabilities for this problem are given as follows:
Mice leaves first -> 4/11.Bat leaves second: -> 7/10.Hence the probability is given as follows:
4/11 x 7/10 = 2/11 x 7/5 = 14/55.
Learn more about the concept of probability at https://brainly.com/question/24756209
#SPJ1
consider a normal population with u= 75 and o= 10. a sample of at least which size needs to be obtained in order to achieve a standard error or om= 2.00 or less.

Answers
n = 25
=====================================================
Explanation:
The standard error formula for the mean is
\(\sigma_{M} = \frac{\sigma}{\sqrt{n}}\\\\\)
Since we want this 2.00 or less, this means,
\(\sigma_{M} \le 2.00\\\\\frac{10}{\sqrt{n}} \le 2.00\\\\10 \le 2.00\sqrt{n}\\\\2.00\sqrt{n} \ge 10\\\\\sqrt{n} \ge \frac{10}{2.00}\\\\\sqrt{n} \ge 5\\\\n \ge 5^2\\\\n \ge 25\\\\\)
The sample size needs to be n = 25 or larger.
In other words, the sample size needs to be at least 25.
Which of the following systems of inequalities has point D as a solution?

Answers
Answer:
f(x) \(\leq\) 3x + 4
g(x) ≥ -1/2x - 5
Step-by-step explanation:
Point D is below f(x) and above g(x)
Helping in the name of Jesus.
What are the values of A, B, C, and D?
A = 0; B = 1; C = -3; D = 3
A = 0; B = 1; C = 3; D = -3
A = 1; B = 0; C = -3; D = 3
A = 1; B = 0; C = 3; D = -3
Don’t know real answer

Answers
The values of A, B, C and D are (d) A = 1, B = 0, C = 3 and D = -3
How to solve for A, B, C and D?From the question, we have:
x^3 + 8x - 3 = Ax^3 + 5Ax + Bx^2 + 5B + Cx + D
Collect like terms
x^3 + 8x - 3 = Ax^3 + Bx^2 + 5Ax + Cx + 5B + D
By comparing the coefficients, we have:
Ax^3 = x^3
Bx^2 = 0
5Ax + Cx = 8x
5B + D = -3
Remove the x factors
A = 1
B = 0
5A + C = 8
5B + D = -3
Substitute A = 1 in 5A + C = 8
5(1) + C = 8
Solve for C
C = 3
Substitute B = 0 in 5B + D = -3
5(0) + D = -3
Solve for B
D = -3
Hence, the values of A, B, C and D are (d) A = 1, B = 0, C = 3 and D = -3
Read more about partial fractions at:https://brainly.com/question/18958301
#SPJ6
HELP I DONT KNOW THIS IS IT A B C OR D

Answers
Answer:
C
Step-by-step explanation:
Because it’s just flipped to the other side
Which of these rational numbers is a repeating decimal? Type all that apply.

Answers
Answer:
- 0.347
2.153
Step-by-step explanation:
Answer:
- 0.347 and 2.153
Hope this helps :)
Explanation below.
Step-by-step explanation:
The lines on top of the decimals tell that the decimal is repeating, and both - 0.347 and 2.153 have lines so they are repeating decimals.
51) Write the equation of the line passing through (-2, 5) and perpendicular x + 3y = 15.

Answers
Answer: plz mark me brainliest
Step-by-step explanation:
I need points to ask a question
Solve the following compound inequality
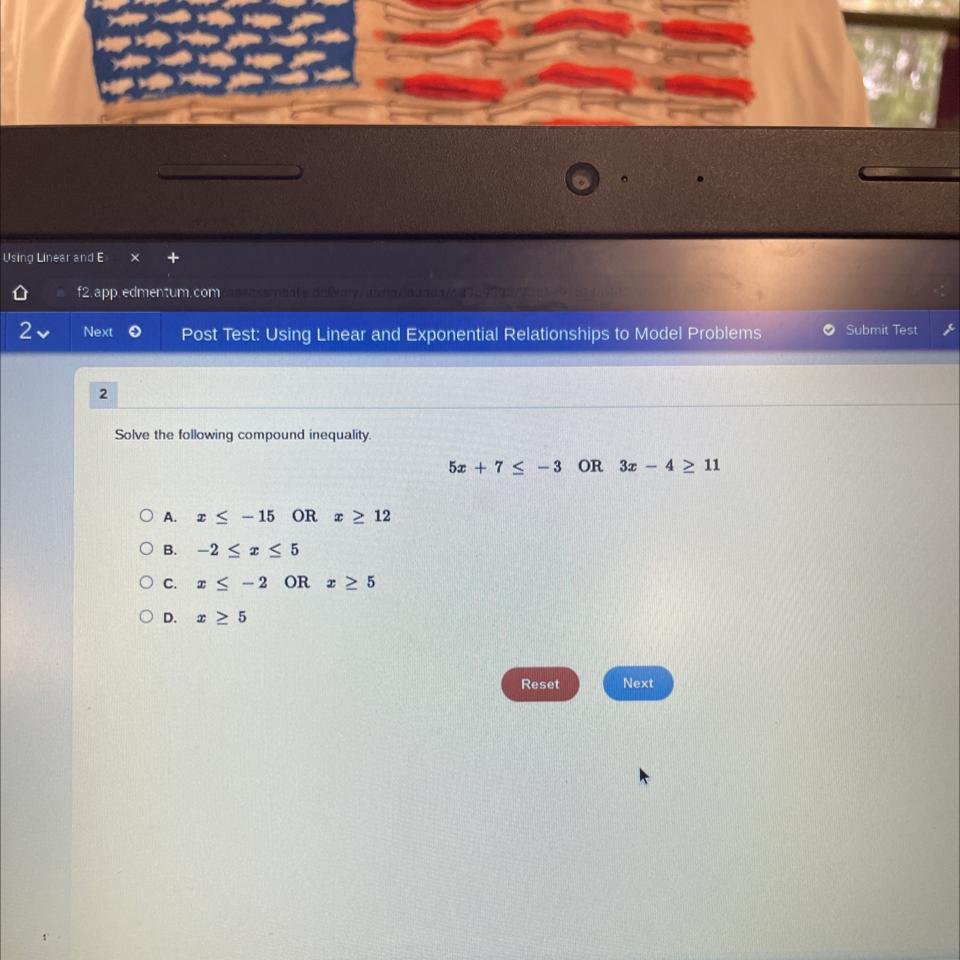
Answers
The solution of the compound inequality 5x + 7 ≤ - 3 or 3x - 4 ≥ 11 is x ≤ -2 or x ≥ 5. Therefore, the answer is C.
How to solve compound inequalities?An inequality is an expression containing <, >, ≤ and ≥.
A compound inequality is an inequality that combines two simple inequalities.
Therefore, let's solve the compound inequality as follows:
5x + 7 ≤ - 3 or 3x - 4 ≥ 11
5x + 7 ≤ - 3
5x ≤ -3 - 7
5x ≤ - 10
divide both sides by 5
x ≤ - 10 / 5
x ≤ -2
3x - 4 ≥ 11
3x ≥ 11 + 4
3x ≥ 15
x ≥ 15 / 3
x ≥ 5
Therefore,
x ≤ -2 or x ≥ 5
learn more on inequality here: https://brainly.com/question/28600203
#SPJ1
Find the length of the line joining A (3,5) and B (1,3)
Answers
Answer:
2√2 units.
Step-by-step explanation:
To find the length of the line joining points A(3, 5) and B(1, 3), we can use the distance formula. The distance formula is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
Substituting the coordinates of points A and B into the formula, we have:
d = sqrt((1 - 3)^2 + (3 - 5)^2)
= sqrt((-2)^2 + (-2)^2)
= sqrt(4 + 4)
= sqrt(8)
= 2sqrt(2)
Therefore, the length of the line joining points A and B is 2√2 units.
Engineers must consider the breadths of male heads when designing helmets. The company researchers have determined that the population of potential clientele have head breadths that are normally distributed with a mean of 6.7-in and a standard deviation of 1.1-in.In what range would you expect to find the middle 50% of most head breadths
Answers
Answer:
\( 6.7 -0.674 *1.1 =5.96\)
\( 6.7 +0.674 *1.1 =7.44\)
Step-by-step explanation:
Let X the random variable that represent the head breadths of a population, and for this case we know the distribution for X is given by:
\(X \sim N(6.7,1.1)\)
Where \(\mu=6.7\) and \(\sigma=1.1\)
We want the range of the middle 50% values on the distribution. Since the normal distribution is symmetrical we know that in the tails we need to have the other 50% and on each tail 25% by symmetry.
We can use the z score formula given by:
\(z=\frac{x-\mu}{\sigma}\)
The critical values that accumulates 0.25 of the area on each tail we got:
\( z_{crit}= \pm 0.674\)
And if we solve x from the z score we got:
\( x = \mu \pm z \sigma\)
And replacing we got:
\( 6.7 -0.674 *1.1 =5.96\)
\( 6.7 +0.674 *1.1 =7.44\)
Object A is moving at 30 ft per sec. Object B is moving at 20 mph.
Answers
Answer:
what we have to find or to prove.
On one day at a local minigolf course, there were 320 customers who paid a total of $2,900. If the cost for a child is $7 per game and the cost for an adult is $10 per game, write a system of equations to model this scenario, where x represents the number of children and y represents the number of adults who played that day.
7x + 10y = 2900
x + y = 320
7x + 10y = 320
x + y = 2900
10x + 7y = 2900
x + y = 320
10x + 7y = 320
x + y = 2900
Brainiest for correct answer
Answers
A system of equations to model this scenario is given as follows -
x + y = 320
7x + 10y = 2900
What is expression?In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context.Mathematical symbols can designate numbers (constants), variables, operations, functions, brackets, punctuation, and grouping to help determine order of operations and other aspects of logical syntax.The general equation of a straight line is → y = mx + c{m} - slope {c} - intercept along the y - axis.
Given is that on one day at a local minigolf course, there were 320 customers who paid a total of $2,900. The cost for a child is $7 per game and the cost for an adult is $10 per game.
Let {x} represents the number of children and {y} represents the number of adults who played that day. We can write the given system of equations as -
x + y = 320
7x + 10y = 2900
Therefore, a system of equations to model this scenario is
x + y = 320
7x + 10y = 2900
To solve more questions on expressing evaluation, visit the link below -
brainly.com/question/1041084
#SPJ1
How many 5/8 inch binder clips, laid side by side, make a length of 11 1/4 inches?
Answers
Answer:
18
Step-by-step explanation:
Because 5/8×18 is 11 1/4
Answer:
what he said
Step-by-step explanation:
The width of a rectangle is 2cm more than 8 times the length. The perimeter is 68cm. What are the width and length of the rectangle?
Answers
Answer:
Length = 3.56cm
Width = 30.48cm
Step-by-step explanation:
We can use the following equation ty o solve
\(68 = 2(2 + 8x) + 2x\)
Length = x
Width = 2 + 8x
Reduce
68 = 4 + 18x
x = 3.56
We then plug x in width equation and get 30.48
Find each product
(n-6)(n+6)
Answers
Answer:
n squared - 10n + 24
Step-by-step explanation:
Need help Do today
2x+y=11
7x=14
Answers
Answer:
{x,y} = {2,7}
Step-by-step explanation:
sorry if i got it wrong
Determine how many liters a right circular cylindrical tank holds if it is 6 m long and 13 m in diameter.
Answers
The tank holds approximately 994,040 liters.
To solve this problem
The volume of a right circular cylinder is given by the formula:
V = πr^2h
Where
r is the radius of the cylinderh is its height π is a mathematical constant approximately equal to 3.14159The cylinder's diameter is specified as 13 m, hence the radius may be computed using the formula: r = d/2 = 13/2 = 6.5 m
The cylinder is described as having a 6 m length.
These values are substituted into the volume calculation to produce the following result:
V = π(6.5)^2(6)
V ≈ 994.04 cubic meters
Since 1 cubic meter equals 1000 liters, we can convert the volume to liters by multiplying by 1000.
V = 994.04 cubic meters x 1000 liters/cubic meter
V = 994,040 liters
Therefore, the tank holds approximately 994,040 liters.
Learn more about volume of cylinder here : brainly.com/question/27535498
#SPJ1
please help and don't say soothing random to get points

Answers
Answer: Last equation (D)
Step-by-step explanation:
Since they want the perpendicular slope, we must take the negative reciprocal if the slope in the equation given. So the negative reciprocal of -1/3 is 3 so that takes out the first and third equation. Now we have to use point slope which is y - y1= m (x - x1) . Doing this gives us y - 5 = 3(x+2) which is the last equation.
A boat crew rowed 105 kilometers downstream, with the current, in 5 hours. The return trip upstream, against the current, covered the same distance, and it took 21 hours. Find the crew is rowing rate in still water.rowing rate=_______ kilometers per hour
Answers
It's important to notice that downstream indicates that the river goes in the same direction that the boat crew, so we add; while upstream they have opposite directions so we subtract.
First, we find the ratio in each case.
\(\begin{gathered} \text{down}=\frac{105\operatorname{km}}{5hr}=21\operatorname{km}/hr \\ up=\frac{105\operatorname{km}}{21hr}=5\operatorname{km}/hr \end{gathered}\)Then, we form the following system
\(\begin{gathered} x+y=21 \\ x-y=5 \end{gathered}\)The first equation is with the current and the second one is against. Let's combine the equations and solve for x
\(\begin{gathered} x+x+y-y=21+5 \\ 2x=26 \\ x=\frac{26}{2} \\ x=13 \end{gathered}\)Therefore, the rowing rate in still water is 13 kilometers per hour.In the triangle below, find the measurements of the unknown angles. a 75 • A. 75 1059 B. 40°. 80° O c. 50, 10° O D. 25°, 50 O E 35°. 70
Answers
answer:
explanation:
hope it helps!


Select the correct answer.
Which graph represents the solutions to this equation?
x2 + 8x = -20
(as a graph pls!)
Answers
Answer:
Step-by-step explanation:

WILL GIVE BRAINLIEST FOR CORRECT ANSWER: All 5 students in Mrs.Awful's class score 50 on a test. What is the class's average score on this test?
Answers
Answer:
50
Step-by-step explanation:
If everyone scored 50, the average is just 50.
The math would also be:
50 + 50 + 50 + 50 + 50 / 5 = 250 / 5 = 50
Answer:
50
Step-by-step explanation:
In short explanation, since all the students scored the same score, the average will be the that score
Since all students scored 50, the average will be 50.
Proof:
\(50 + 50 + 50 + 50 + 50 = 250\)
\(250 \div 5 = 50\)
A pizza company runs a marketing campaign based on their delivery time for pizzas. They claim that they will deliver a pizza within 30 minutes of ordering or it is free. In practice the time it takes to prepare a pizza and it being delivered is normally distributed with mean 25 minutes and standard deviation 3 minutes. What is the probability a pizza is delivered for free?On a particular Sunday, 40 pizzas were ordered. What is the probability that more than 2 were delivered for free?If the company wants to reduce the proportion of pizzas that are delivered free to 1%, what should the delivery time be advertised as?
Answers
Answer:
0.0475 = 4.75% probability a pizza is delivered for free.
0.2955 = 29.55% probability that more than 2 were delivered for free.
The delivery time should be advertised as 32 minutes.
Step-by-step explanation:
To solve this question, we need to understand the binomial distribution and the normal distribution.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
In which \(C_{n,x}\) is the number of different combinations of x objects from a set of n elements, given by the following formula.
\(C_{n,x} = \frac{n!}{x!(n-x)!}\)
And p is the probability of X happening.
Normal Probability Distribution:
Problems of normal distributions can be solved using the z-score formula.
In a set with mean \(\mu\) and standard deviation \(\sigma\), the z-score of a measure X is given by:
\(Z = \frac{X - \mu}{\sigma}\)
The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the p-value, we get the probability that the value of the measure is greater than X.
Normally distributed with mean 25 minutes and standard deviation 3 minutes.
This means that \(\mu = 25, \sigma = 3\)
What is the probability a pizza is delivered for free?
More than 30 minutes, which is 1 subtracted by the p-value of Z when X = 30.
\(Z = \frac{X - \mu}{\sigma}\)
\(Z = \frac{30 - 25}{3}\)
\(Z = 1.67\)
\(Z = 1.67\) has a p-value of 0.9525
1 - 0.9525 = 0.0475
0.0475 = 4.75% probability a pizza is delivered for free
What is the probability that more than 2 were delivered for free?
Multiple pizzas, so the binomial probability distribution is used.
0.0475 probability a pizza is delivered for free, which means that \(p = 0.0475\)
40 pizzas, which means that \(n = 40\)
This probability is:
\(P(X > 2) = 1 - P(X \leq 2)\)
In which
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2)\)
So
\(P(X = x) = C_{n,x}.p^{x}.(1-p)^{n-x}\)
\(P(X = 0) = C_{40,0}.(0.0475)^{0}.(0.9525)^{40} = 0.1428\)
\(P(X = 1) = C_{40,1}.(0.0475)^{1}.(0.9525)^{39} = 0.2848\)
\(P(X = 2) = C_{40,2}.(0.0475)^{2}.(0.9525)^{38} = 0.2769\)
Then
\(P(X \leq 2) = P(X = 0) + P(X = 1) + P(X = 2) = 0.1428 + 0.2848 + 0.2769 = 0.7045\)
\(P(X > 2) = 1 - P(X \leq 2) = 1 - 0.7045 = 0.2955\)
0.2955 = 29.55% probability that more than 2 were delivered for free.
If the company wants to reduce the proportion of pizzas that are delivered free to 1%, what should the delivery time be advertised as?
The 99th percentile, which is X when Z has a p-value of 0.99, so X when Z = 2.327.
\(Z = \frac{X - \mu}{\sigma}\)
\(2.327 = \frac{X - 25}{3}\)
\(X - 25 = 2.327*3\)
\(X = 32\)
The delivery time should be advertised as 32 minutes.
Question 2
On holiday you change £350 into Dollars and receive $588
If you used these Dollars to buy a gift for $126, how much does the gift cost in pounds?
Answers
The cost of the gift in the pounds is a 107.10 Pounds.
According to the statement
we have to find the cost of the gift in the pounds.
So, For this purpose, we know that the
The pound is the main unit of sterling, and the currency itself may be referred to by the compound noun pound sterling or the term British pound.
From the given information:
you change 350 pounds into dollars and get 588 dollars.
And the price of gift in dollars is a 126.
We know that the
1 Pound sterling equals to the 1.68 United States Dollar
it means
350 pounds in dollars = 1.68 *350
350 pounds in dollars = 588 dollars
And according to this
1 dollar = 0.85 pounds
So,
126 dollars into pounds = 126*0.85
126 dollars into pounds = 107.10 Pounds.
So, The cost of the gift in the pounds is a 107.10 Pounds.
Learn more about pounds here
https://brainly.com/question/2202418
#SPJ9
A ship X sailing with a velocity (21 kmh 052⁰) observes a light fron a lighthuse due North. The bearing of the liglhthouse from the ship 20 minutes later is found to be 312. calcuate correct to thre sigificant figures
i) the orignal distance when the lighthoues is due West of the ship from the time when it is due North of the ship.
ii) the time in minutes, when the lighthouse is due West of the ship from the time when it is due North of the ship.
iii) the distance in km of the ship from the lighthoue when the light.hose is due West of the ship
Answers
i) the original distance when the lighthouse is due West of the ship is 7 km
ii) The time in minutes when the lighthouse is due West of the ship is 21 minutes
iii) The distance in km of the ship from the lighthouse when the lighthouse is due West of the ship is 29.97 km
To solve this problem, we'll use the concepts of relative velocity and trigonometry. Let's break down the problem into three parts:
i) Finding the original distance when the lighthouse is due West of the ship:
The ship's velocity is given as 21 km/h at a bearing of 052°. Since the ship observed the lighthouse due North, we know that the angle between the ship's initial heading and the lighthouse is 90°.
To find the distance, we'll consider the ship's velocity in the North direction only. Using trigonometry, we can determine the distance as follows:
Distance = Velocity * Time = 21 km/h * (20 min / 60 min/h) = 7 km (to three significant figures).
ii) Finding the time in minutes when the lighthouse is due West of the ship:
To find the time, we need to consider the change in angle from 052° to 312°. The difference is 260° (312° - 052°), but we need to convert it to radians for calculations. 260° is equal to 260 * π / 180 radians. The ship's velocity in the West direction can be calculated as:
Velocity in West direction = Velocity * cos(angle) = 21 km/h * cos(260 * π / 180) ≈ -19.98 km/h (negative because it's in the opposite direction).
To find the time, we can use the formula:
Time = Distance / Velocity = 7 km / (19.98 km/h) = 0.35 h = 0.35 * 60 min = 21 minutes (to three significant figures).
iii) Finding the distance in km of the ship from the lighthouse when the lighthouse is due West of the ship:
We can use the formula for relative velocity to find the distance:
Relative Velocity = sqrt((Velocity in North direction)² + (Velocity in West direction)²)
Using the values we calculated earlier, we have:
Relative Velocity = sqrt((21 km/h)² + (-19.98 km/h)²) ≈ 29.97 km/h (to three significant figures).
Therefore, the ship is approximately 29.97 km away from the lighthouse when the lighthouse is due West of the ship.
For more question on distance visit:
https://brainly.com/question/30395212
#SPJ8
The diameters of bolts produced in a machine shop are normally distributed with a mean of 5.48 millimeters and a standard deviation of 0.07 millimeters. Find the two diameters that separate the top 3% and the bottom 3%. These diameters could serve as limits used to identify which bolts should be rejected. Round your answer to the nearest hundredth, if necessary.
Answers
The two diameters that separate the top 35 from the bottom 35 in the normal distribution are 5.35 mm and 5.61 mm .
Normal distributions are crucial to statistics because they are widely used in the natural and social sciences to represent real-valued covariates whose distributions are unknown.
Some of their significance comes from the main limit theorem. This claim states that, in some cases, the average of many samples (observations) of a stochastic process with limited mean and variance constitutes itself as a random variable, whose distribution tends to become more normal as the number of samples increases. Because of this, the distributions of physical quantities, like misspecification, which are thought to be the consequence of hundreds of distinct processes, are frequently close to normal.First we will find the bottom 3% such that P(X ≤ x) = 0.03
⇒ \(P(\frac{X-5.48}{0.07}\leq \frac{x-5.48}{0.07} )=0.03\)
⇒\(P(Z\leq \frac{x-5.48}{0.07} )=0.03\)
Now we will use the normal table to calculate the corresponding z-score.
\(\frac{x-5.48}{0.07} =-1.88\\\\\implies x = 5.348\)
Now we will find the same for the top part of the distribution.
\(P(\frac{X-5.48}{0.07}\leq \frac{x-5.48}{0.07} )=0.97\\\\\implies P(Z\leq \frac{x-5.48}{0.07} )=0.97\)
Now we will use the normal table to calculate the corresponding z-score.
\(\frac{x-5.48}{0.07} =1.88\\\\\implies x = 5.612\)
The two diameters that separate the top 35 from the bottom 35 in the normal distribution are 5.35 mm and 5.61 mm .
To learn more about normal distribution visit:
https://brainly.com/question/14916937
#SPJ1
Mrs. Fields needs more chocolate chips to make cookies. The store has bags that weigh 0.45 lbs., 0.434 lbs., and 0.4 lbs. Which bag should she purchase if she wants the most chocolate chips?
Answers
Answer:
bag weigh 0.45 lbs
Step-by-step explanation:
