How many unique sets of 3 prime numbers exist for which the sum of the numbers is 44?

The area of region of the function f on the interval [1, 2] is found to be 3/2 square units using the integration.

In calculus, integration can be used to find the area of the region under a curve.

In this case, we want to find the area of the region under the graph of the function f on the interval [1, 2], where

f(x) = ∫3/2 square units.

We can start by graphing the function on the interval [1, 2]:

We can see that the graph of f is a horizontal line at y = 3/2 between x = 1 and x = 2.

Therefore, the area of the region under the graph of f on the interval [1, 2] is simply the area of a rectangle with base 1 and height 3/2:

Area = base x height

= 1 x 3/2

= 3/2 square units.

The area of the region under the graph of the function f on the interval [1, 2] is 3/2 square units.

Know more about the area of region

https://brainly.com/question/1297097

#SPJ11

Answer:

A. Sample space = 6

B. 0.17

C. No

D. Yes

Step-by-step explanation:

A. The sample space of an experiment is the set of all possible outcomes of that experiment.

since there are three colours and 2 outcomes for a coin toss,

sample space = 3 * 2 = 6

B. Probability of picking a green first = 4/12 = 1/3

probability of a tail = 1/2

Probability of a green and a tail, P(A) = 1/3 * 1/2 = 0.17

C. No.

Considering the two events;

A; green card is picked first

C ; a green or red card is picked

There is an intersection point for the two events.  Therefore, they are not mutually exclusive.

D. Yes.

Considering the two events;

A; green card is picked first

B ; a blue or red card is picked

There is no intersection point for the two events. Therefore, they are mutually exclusive.

The probability of her winning is 1/5.

We have that odds in favor of a particular event are given by Number of favorable outcomes to Number of unfavorable outcomes. This is:

Therefore, odds in favor of the winning is

Answer: 1 : 4

Answer:

The probability is 20%.

Step-by-step explanation:

convert the fraction into percentage.

Chad used the scale of 1 scale inch which is equal to 9 feet.

In the conventional system of measuring, an inch is a unit of length. Either in or " can be used to denote length in inches. For instance, 16 in or 16" can be used to write 5 inches.

Given that,

The length of the gym in real life = 81 feet

The length of the gym in scale drawing = 9 inches

1 scale inch = length of the gym in real life/length of the gym in the scale drawing

1 scale inch = 81/9 = 9

Thus, Chad used the scale of 1 scale inch which is equal to 9 feet.

To know more about scale inch visit: brainly.com/question/30129840

#SPJ4

Answer:

The slope of the line is 3 and the y-intercept is (3/2) three-halves.

Step-by-step explanation:

The data provided is:

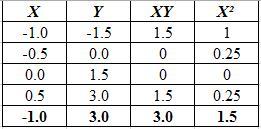
 X     Y

-1.0     -1.5

-0.5     0.0

0.0     1.5

0.5     3.0

The slope of the linear function is denoted by, b and the intercept is denoted by, a.

The formula to compute the slope and intercept are:

\(a &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} \\\\b &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2}\)

Compute the values required in Excel.

Compute the slope and intercept as follows:

\(a &= \frac{\sum{Y} \cdot \sum{X^2} - \sum{X} \cdot \sum{XY} }{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = \frac{ 3 \cdot 1.5 - (-1) \cdot 3}{ 4 \cdot 1.5 - (-1)^2} \approx \frac{3}{2} \\ \\b &= \frac{ n \cdot \sum{XY} - \sum{X} \cdot \sum{Y}}{n \cdot \sum{X^2} - \left(\sum{X}\right)^2} = \frac{ 4 \cdot 3 - (-1) \cdot 3 }{ 4 \cdot 1.5 - \left( -1 \right)^2} \approx 3\end{aligned}\)

Thus, the slope of the line is 3 and the y-intercept is (3/2) three-halves.

Answer:

D: The slope is 3, and the y-intercept is 3/2

Step-by-step explanation:

I got it correct on Edge 2020

Answer: Option C, the median is 5.

Step-by-step explanation:

The median is the value that is just in the middle of our data set (the possible values in the histogram)

the set is S = {2, 3, 4, 5, 6, 7, 8, 9}

And if we take in account the number of times that each value is repeated, we get:

S = {2, 3, 3, 4, 4, 4, 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 9}

So we have 17 values, and the one exactly in the middle will be the median.

To find the point in the middle, we can use that we have 17 values, because 17 is odd, we can do

17 - 1 = 16

16/2 = 8.

17 - 8 = 9.

Then the 9nth point is our median:

the 9th point is a 5.

Then the correct option is C

Answer: 22/13

Step-by-step explanation:

65e = 110

Divide 63 on both sides anyou get 22/13

The value of the given integral is - (√3/3).

The integral given is ∫4√3 dx S √√64-x² 0. To evaluate this integral, we need to make a substitution that will simplify the integrand. The most helpful substitution for this integral is x = 8 sin θ (option B).

Using this substitution, we can rewrite the integral as ∫4√3 cos θ dθ from 0 to π/6. We can then simplify the integrand by using the identity cos 2θ = 1 - 2sin²θ and substituting u = sin θ.

This gives us the integral ∫(4√3/2)(1 - u²) du from 0 to 1/2.

Integrating this expression, we get [(4√3/2)u - (4√3/6)u³] from 0 to 1/2, which simplifies to (2√3/3) - (32√3/48) = (√3/3) - (2√3/3) = - (√3/3).

Therefore, the value of the given integral is - (√3/3).

To know more about integral refer here:

https://brainly.com/question/31433890#

#SPJ11

Answer:

The Total Surface Area of cone is 264 cm²

Step-by-step explanation:

Radius (r) = 6 cm

Slant height (l) = 8 cm

To find TSA of cone

A = πr(l + r)

A = 22/7 × 6 × (8 + 6)

A = 22/7 × 6 × (14)

A = 22/7 × 84

A = 22 × 12

A = 264 cm²

Thus, The Total Surface Area of cone is 264 cm²

-TheUnknownScientist 72

The probability that a person arriving to use the machine will find it idle is 1/3 or 0.3333. Option a is correct.

Use the concept of an M/M/1 queue to calculate the probability, which models a single-server queue with exponential interarrival times and exponential service times.

In this case, the interarrival time follows an exponential distribution with a rate parameter of λ = 5 persons per hour (or 1/12 persons per minute). The service time (copying time) also follows an exponential distribution with a rate parameter of μ = 1/8 persons per minute (since each person uses the machine for an average of 8 minutes).

In an M/M/1 queue, the probability that the system is idle (no person is being served) can be calculated as:

P_idle = ρ⁰ × (1 - ρ), where ρ is the traffic intensity, defined as the ratio of the arrival rate to the service rate. In this case, ρ = λ/μ.

Plugging in the values, we have:

ρ = (1/12) / (1/8) = 2/3

P_idle = (2/3)⁰ × (1 - 2/3) = 1/3

Therefore, the probability is 1/3 or approximately 0.3333.

Thus, option (A) is the correct answer.

Learn more about probability https://brainly.com/question/31828911

#SPJ11

The measure of angle c is 70 degrees.

If angle a and angle b are complementary, it means that the sum of their measures is equal to 90 degrees.

Given:

Measure of angle a = 10x + 10

Measure of angle b = 20

We can set up the equation:

(10x + 10) + 20 = 90

Simplifying the equation:

10x + 30 = 90

Subtracting 30 from both sides:

10x = 60

Dividing both sides by 10:

x = 6

Now, we have found the value of x to be 6.

To find the measure of angle c, we can substitute the value of x into the equation for angle a:

Measure of angle a = 10x + 10

Measure of angle a = 10(6) + 10

Measure of angle a = 60 + 10

Measure of angle a = 70

As a result, angle c has a measure of 70 degrees.

for such more question on angle

https://brainly.com/question/25716982

#SPJ8

Answer:

610

Step-by-step explanation:

Given:

Add:

259 + 431 = 690

Subtract:

1300 - 690 = 610

So, on Wednesday 610 emails were sent out.

Hope this helped.

On average, a customer spends approximately 1.16 minutes waiting time on hold before they can start speaking to a representative.

To find the average waiting time for a customer on hold before they can start speaking to a representative, we need to consider both the arrival rate of calls and the average service time of the staff members.

Given:

9 staff members taking calls.

On average, one call arrives every 5 minutes (standard deviation of 5 minutes).

Each staff member spends on average 18 minutes with each customer (with a standard deviation of 27 minutes).

To calculate the average waiting time, we need to use queuing theory, specifically the M/M/c queuing model. In this model:

"M" stands for Markovian or memoryless arrival and service times.

"c" represents the number of servers.

In our case, we have an M/M/9 queuing model since we have 9 staff members.

The average waiting time for a customer on hold is given by the following formula:

Waiting time = (1 / (c * (μ - λ))) * (ρ / (1 - ρ))

Where:

c = number of servers (staff members) = 9

μ = average service rate (1 / average service time)

λ = average arrival rate (1 / average interarrival time)

ρ = λ / (c * μ)

First, let's calculate the average arrival rate (λ):

λ = 1 / (average interarrival time) = 1 / 5 minutes = 0.2 calls per minute

Next, calculate the average service rate (μ):

μ = 1 / (average service time) = 1 / 18 minutes = 0.0556 customers per minute

Now, calculate ρ:

ρ = λ / (c * μ) = 0.2 / (9 * 0.0556) ≈ 0.407

Finally, calculate the waiting time:

Waiting time = (1 / (c * (μ - λ))) * (ρ / (1 - ρ))

= (1 / (9 * (0.0556 - 0.2))) * (0.407 / (1 - 0.407))

≈ 1.16 minutes

Therefore, on average, a customer spends approximately 1.16 minutes waiting on hold before they can start speaking to a representative.

For more details about waiting time

https://brainly.com/question/24168195

#SPJ4

The area of the remaining rectangular plot of land is 4680m²

Area of rectangle:

Area of rectangle means the area covered by the rectangle.

The formula for area of rectangle is

A = l x b

where,

l is the length of the rectangle

b is the breadth or width of the rectangle

Given,

A rectangular plot of land measures 40.0 m by 120.0 m, with a parcel 10.0 m by 12.0 m out of one corner for an electrical transformer.

Here we need to find the remaining area of the rectangular plot land.

For that first, we have to find the area of each separately,

Like,

The area of the rectangular plot is,

A₁ = 40.0 x 120.0 m²

A₁ = 4800m²

Similarly, the area of the electric transformer is,

A₂ = 10.0 x 12.0 m²

A₂ = 120m²

Now the remining area is,

A = A₁ - A₂

A = 4800 - 120 m²

A = 4680m²

Therefore, the area of the remaining rectangular plot is 4680m².

To know more about Area of rectangle here.

https://brainly.com/question/20693059

#SPJ4

well, from 273 to 250 is 23 bucks, so that's the difference.

we know 273 is the original price, or namely the 100%, so what's 23 bucks off of it in percentage?

\(\begin{array}{ccll} amount&\%\\ \cline{1-2} 273&100\\ 23&x \end{array}\implies \cfrac{273}{23}=\cfrac{100}{x}\implies \implies 273x=2300 \\\\\\ x=\cfrac{2300}{273}\implies x\approx 8.42\)

Answer:

80000000000000x200000004500 =

1.6e+25 which is essentially 1.6 with 25 0's after it

Step-by-step explanation:

May I have brainliest please? I'm trying to get 15 and I'm so close :)

Answer:

9

Step-by-step explanation:

63+9=72

72/8=9

hope this helped

Answer:

\(8n - 9 = 63 \\ 63 + 9 = 8n \\ 72 \div 8 = n \\ n = 9\)

Answer:

So that it can run faster

Answer:

\(a = change \: in \: v \div time\)

Step-by-step explanation:

Change in V =28-0

=28

time =4 sec

Therefore acceleration =28 ÷4

7m/s^-2

Prevalence rates are a measure of how common a disease is in a population.

To calculate the prevalence rate, you would divide the number of current cases of the disease by the total population at risk of the disease. This can give you an idea of the overall burden of the disease in a given population. It's important to note that prevalence rates can vary depending on factors such as age, gender, geographic location, and other demographic or health-related factors. Additionally, prevalence rates can change over time as new cases are identified and as treatments or prevention strategies are implemented. Overall, understanding the prevalence of a disease can help public health officials and healthcare providers identify areas of need and develop targeted interventions to reduce the impact of the disease on affected populations.

To know more about prevalence rates, visit:

https://brainly.com/question/14375847

#SPJ11

Answer: The building is 54 feet tall.

Step-by-step explanation:

Both the computers will take 18 minutes to do the job together.

The slower computer sends all the company's email in 45 minutes.

The faster computer completes the same job in 30 minutes.

Let's take minutes t  to complete the task together.

As they complete one job, we get the following equation:

\(\frac{t}{45}\)+\(\frac{t}{30}\)=1

LCM of 45 and 30 is:

45 = 3 x 3 x 5

30 = 2 x 3 x 5

LCM = 2 x 3 x 3 x 5 = 90

Now, solving for t;

⇒\(\frac{2t+3t}{90} = 1\\\frac{5t}{90} =1\\5t=90\\\)

Dividing both sides by 5;

\(\frac{5t}{5}=\frac{90}{5}\)

We get t = 18

Hence, it will take both the computers 18 minutes to do the job together.

A company has two large computers. The slower computer can send all the company's emails in 45 minutes. The faster computer can complete the same job in 30 minutes. If both computers are working together, how long will it take them to do the job?

Learn more about work and time here https://brainly.com/question/13086625

#SPJ4

The new vector →u - →v is 〈 −10,5 〉. Hence, the correct option is (A) 〈 −10,5 〉.

Given vectors are →u = 〈 −6,−1 〉 and →v = 〈 4,−6 〉.We need to find the new vector →u − →v.Vector subtraction can be found by adding the additive inverse of the vector which we want to subtract. Therefore, the additive inverse of vector →v = 〈 4, −6 〉 is 〈 −4, 6 〉.Now, →u − →v  = →u + (−→v)  =  〈 −6,−1 〉 + 〈 −4,6 〉= 〈 −6−4,−1+6 〉 = 〈 −10,5 〉.Therefore, the new vector →u - →v is 〈 −10,5 〉. Hence, the correct option is (A) 〈 −10,5 〉.

Learn more about vector :

https://brainly.com/question/15709504

#SPJ11

Answer:

375\(\sqrt[n]{x}\)

Step-by-step explanation:

Answer: A. 1/11

B. 2/11

C. 0

D. 1/11

Hope this helps!

Answer:

6-11

Step-by-step explanation:

By applying dilatation and congruency theorem, it can be concluded that the distance between points R and R' is 3 units (option A).

Dilation is a transformation of a geometric shape, either becoming larger or smaller, without changing the original shape using a certain scale factor.

Two shapes are said to be congruent if a pair of corresponding sides have the same ratio and the corresponding angles have the same measure.

From the problem we obtained the following information:

QR is dilated to create Q'R' ⇒ QR // Q'R'

The dilatation factor is 1.5 ⇒ Q'R'/QR = 1.5

Now we look at the ΔTRQ and ΔTR'Q':

QR // Q'R'

∠TRQ = ∠TR'Q'

So ΔTRQ is congruent to ΔTR'Q' and TR'/TR = Q'R'/QR

Now we can calculate y using this equation:

   TR'/TR = Q'R'/QR

(6 + y) / 6 = 1.5

      6 + y = 9

            y = 3

Thus, the distance between points R and R' is 3 units.

To learn about dilatation, click here: https://brainly.com/question/29474743

#SPJ4

Complete question :

From a barrel of colored marbles, you randomly select 1 blue 6 yellow 7 red 4 green and 6 purple marbles. Find the experimental probability of randomly selecting a marble that is NOT yellow.

Answer:

Step-by-step explanation:

Total number of marbles :

Blue = 1 ; yellow = 6 ; red = 7 ; green = 4 ; purple = 6

Total = (1 + 6 + 7 + 4 + 6) = 24 marbles

Probability of selecting marble that is not yellow :

Number of marbles that aren't yellow / total number of marbles

Marbles that aren't yellow = 24 - 6 = 18

P(selecting a marble that isn't yellow) = 18 / 24 = 3/4

Answer: 12

Step-by-step explanation:

Answer:

D

Step-by-step explanation:

Given a tangent and a secant from an external point to the circle, then

The product of the external part and the whole secant is equal to the square of the tangent, that is

8(8 - 6 + 2x) = 12²

8(2 + 2x) = 144 ( divide both sides by 8 )

2 + 2x = 18 ( subtract 2 from both sides )

2x = 16 ( divide both sides by 2 )

x = 8

Then

GH = - 6 + 2x = - 6 + 2(8) = - 6 + 16 = 10 → D

Answer:

\(\textsf{GH=10}\)

Step-by-step explanation:

\((EF)^{2} =FG(FH)\)

\((12)^{2} =8(8-6+2x)\)

\(144=8(2+2x)\)

\(144=16+16x\)

\(16x=144-16\)

\(16x=128\)

\(x=128/16=8\)

So, \(GH=-6+2(8)=\)

\(-6+16=\)

\(=10\)

\(\textsf{OAmalOHopeO}\)

To approximate the area under the curve y = x³ from x = 3 to x = 7 using a right endpoint approximation with 6 subdivisions, the formula for Right Endpoint Approximation is:

RIEMANN SUM = ∑ f(xi)Δx

The interval is divided into n equal parts which can be expressed as:

Δx = (b - a) / n

where a and b are the lower and upper bounds respectively, n is the number of subdivisions.

Δx = (7 - 3) / 6 = 4 / 6 = 0.6666666667

Then, we can calculate the values of xi:

xi = a + iΔx

x0 = 3

x1 = 3.6666666667

x2 = 4.3333333333

x3 = 5

x4 = 5.6666666667

x5 = 6.3333333333

x6 = 7

We can now substitute the values of xi into the function, f(x) = x³ and obtain the values of f(xi).

f(x0) = 3³ = 27

f(x1) = 3.6666666667³ = 50.847221820371

f(x2) = 4.3333333333³ = 84.703703672997

f(x3) = 5³ = 125

f(x4) = 5.6666666667³ = 189.58271616609

f(x5) = 6.3333333333³ = 273.96296293926

f(x6) = 7³ = 343

Now, the Riemann sum can be obtained using the formula above.

RIEMANN SUM = ∑ f(xi)Δx

= [f(x0) + f(x1) + f(x2) + f(x3) + f(x4) + f(x5) + f(x6)]Δx

= [27 + 50.847221820371 + 84.703703672997 + 125 + 189.58271616609 + 273.96296293926 + 343] × 0.6666666667

= 1598.5479336901

Therefore, the approximate area under the curve y = x³ from x = 3 to x = 7 using a right endpoint approximation with 6 subdivisions is 1598.5479336901.

To learn more about approximation, refer below:

https://brainly.com/question/29669607

#SPJ11