how many meters in 200 km
Answers
Related Questions
2. Help me find the mode of these data set: 12, 10, 10, 10, 13,12, 11, 13, 10
(2 Points)
1. 10
2. 10 & 12
3. no mode
4. 12
Answers
Answer:
10 is the answer for this
please mark me as brilliant
I don’t know what I’m doing wrong for this

Answers
Answer:
Step-by-step explanation:
I guess you want to draw the graph.
The graph is a straight line
-6x - 20 = 4y
When x = 0:
-6(0) - 20 = 4y
y = -20/4 = -5
So, one point on the graph
= (0, -5)
When y = -2:
Plugging y = -2 into the equation:
-6x - 20 = 4(-2)
-6x = -8 + 20 = -12
x = -2
So, another point is (-2, -2)
Mark these 2 points on the graph paper
and draw a line passing through them.
Scientists often use a process called carbon dating to estimate the age of archaeological finds. The process measures the amount of carbon-14, a: radioactive isotope with a halfflife of 5,730 years. If a sample of wood from an ancient artifact had 20 grams of carbon-14 initially, the amount remaining, in grams, is given by A(t)=20(1/2) v/S,730 where tis the number of years since the tree died. How many grams would be present after 5,730 years? Select one: a. 40 g
b. 0.27 g
c. 5 g
d. 109
Answers
After 5,730 years, 10 grams of carbon-14 would be present.
Scientists often use a process called carbon dating to estimate the age of archaeological finds. The process measures the amount of carbon-14, a: radioactive isotope with a half life of 5,730 years. If a sample of wood from an ancient artifact had 20 grams of carbon-14 initially, the amount remaining, in grams, is given by :
A(t)=20(1/2) ^ (t/5,730)
Substituting t = 5,730 in the given equation, we get:
A(5,730) = 20(1/2)^(5,730/5,730)
Simplifying, we get:
A(5,730) = 20(1/2)^1
A(5,730) = 20(1/2)
A(5,730) = 10
Hence, after 5,730 years, 10 grams of carbon-14 would be present.
To learn more about carbon dating visit : https://brainly.com/question/15673495
#SPJ11
A bank account starts with $3.00. The amount in the account doubles every year .
Answers
Answer:
Step-by-step explana
multiply it by 2 or sdd itself to it
The account will have $1536.007 after 9 years.
Part A:
To express the total amount of money A(t) in the account after 7 years, we can use the formula:
A(t) = P\((2^t)\)
where:
A(t) is the total amount in the account after t years,
P is the initial amount in the account (starting with $3.00 in this case),
t is the number of years.
Substituting the values into the formula, we get:
A(t) = 3 (\(2^7\))
A(t) = 3 x 128
A(t) = 384
Therefore, the total amount of money in the account after 7 years is $384.
B) To find out after how many years the account will have $1536.007, we need to solve the equation:
1536.007 = 3 \((2^t)\)
Dividing both sides of the equation by 3, we get:
512.0023333333 = \(2^t\)
Taking the logarithm (base 2) of both sides, we have:
log2(512.0023333333) = t
t = 9.000317.
Therefore, the account will have $1536.007 after 9 years.
Learn more about Equation here:
https://brainly.com/question/29538993
#SPJ2
−8x 4y>3 6x−7y<−5 is (2,3) a solution of the system?
Answers
The ordered pair (2,3) is not a solution of the system
How to determine if (2,3) a solution of the system?From the question, we have the following parameters that can be used in our computation:
−8x + 4y > 3
6x - 7y < −5
The solution is given as
(2, 3)
Next, we test this value on the system
So, we have
−8(2) + 4(3) > 3
-4 > 3 --- false
This means that (2,3) is not a solution of the system
Read more about inequality at
https://brainly.com/question/32124899
#SPJ4
At Modern Fashion, each week that a coat that costs $120 does not sell the price is reduced, the sequence describes the deduction in the price: $120.00, $107.50, $95.00, $82.50 What will be the price of the coat after the sixth week? Write the recursive and explicit for Modern Fashion.
Answers
Answer:$57.50
Step-by-step explanation:
Recursive formula:
Let P(n) represent the price of the coat in the nth week.
P(n) = P(n-1) - $12.50
Explicit formula:
To find the price of the coat in any given week directly, we can use the following formula:
P(n) = $120 - $12.50 * (n-1)
Using the explicit formula, we can calculate the price after the sixth week:
P(6) = $120 - $12.50 * (6 - 1)
= $120 - $12.50 * 5
= $120 - $62.50
= $57.50
i think
After the sixth week, the price of the coat will be $57.50.
Recursive formula: P(n) = P(n-1) - 12.50, where P(n) is the price of the coat on the nth week.
Explicit formula: P(n) = 132.50 - 12.50n, where P(n) is the price of the coat on the nth week.
i need help on this and yea

Answers
Answer:
3
Step-by-step explanation:
PLSS HELPPP ME IM BEGGING ITS FOR A TEST DUE IN 5 MINS!!!!!!!!!!!!!!!!!!

Answers
Answer:
d
Step-by-step explanation:
the product of z and the complex number 5-6i is a real number. find two possible nonzero values of z.
Answers
To find the values of z that make the product with the complex number 5-6i a real number, we need to consider the imaginary part of the product.
The product of z and 5-6i can be written as:
z * (5 - 6i)
Expanding this expression, we get:
5z - 6zi
For the product to be a real number, the imaginary part (-6zi) must be equal to zero. This means that the coefficient of the imaginary unit i, which is -6z, must be zero.
Setting -6z = 0, we find:
z = 0
So, one possible nonzero value of z is 0.
However, since we are looking for nonzero values of z, we need to find another value that satisfies the condition.
Let's consider the equation for the imaginary part:
-6z = 0
Dividing both sides of the equation by -6, we have:
z = 0/(-6)
z = 0
Again, we find z = 0, which is not a nonzero value.
Therefore, there are no other nonzero values of z that make the product with the complex number 5-6i a real number. The only value that satisfies the condition is z = 0.
A driver travels 208 miles in 4 hours. what is the driver's speen,in miles per hour ?
___miles per hour
Answers
Answer:
52
Step-by-step explanation:
miles per hour so 208, which is miles and 4 which is hours so 208/4 which is 52
Answer:
Hi there,
52 miles/hr
Step-by-step explanation:
we just divide 208 by 4
A plane travels a distance of 3,300 miles at a rate of 550 mph. How long will it take
the plane to reach its destination?
Answers
Answer:
6 hours
Step-by-step explanation:
Divide 3300 by 550, so it's 6.
A chair cost $250 last year and $175 this year by what percent did the price decrease?
Answers
Answer:
I believe it is 50% decreased, not sure
Step-by-step explanation:
Answer:
30%
Step-by-step explanation:
in order to find the percentage of the price decrease,we must find the difference between the prices
250-175=75
the price has dropped 75$
to find the percentage, we do 75/250
which can be simplified to 3/10 or 30%
We can check this by finding 30% of 250 which is 75
75=75
Please help ASAP I’ll mark you as brainlister

Answers
The cost of 7 chairs and 2 tables is equal.If the cost of 6 chairs and 5 tables is 10575, find the cost of 12 chairs.
Answers
Answer:
5400
Step-by-step explanation:
Let x represent the cost of a chair and y represent the cost of a table. We can use this to set up a system of equations:
7x=2y
6x+5y=10575
We can solve this system using substitution.
Start by rewriting the first equation in terms of x.
\(7x=2y\\\text{Divide both sides by 7}\\x=\frac{2}{7}y\)
Substitute this into the second equation:
\(6(\frac{2}{7}y)+5y=10575\\\frac{12}{7}y+5y+10575\\\frac{12}{7}y+\frac{35}{7}y=10575\\\frac{47}{7}y=10575\)
Multiply both sides by 7
\(47y=74025\)
Divide both sides by 47
\(y=1575\)
This means...
\(7x=2(1575)\\7x=3150\)
Divide both sides by 7
\(x=450\)
One chair costs 450. Now, multiply this number by 12 to find the cost of 12 chairs.
\(450*12=5400\)
12 chairs cost 5400.
- My family wants to start a food business. Every Sunday, the family prepares the best dishes. We need a loan to start our business as a family. We decided to get an SBA Loan and they offered a PPP (Paycheck Protection Program) loan option. The initial amount will be 20,000. This loan has an interest 4. 5% compounded quarterly. What will be the account balance after 10 years?
I’ll mark as BRANLIEST!!
35 POINTS!!
Answers
This loan has an interest 4. 5% compounded quarterly, account balance after 10 years:
The initial loan amount is $20,000, and it has an interest rate of 4.5% compounded quarterly. You would like to know the account balance after 10 years.
To calculate the account balance, we will use the compound interest formula:
A = P(1 + r/n)^(nt)
Where:
A = the future value of the loan
P = the initial loan amount ($20,000)
r = the annual interest rate (0.045)
n = the number of times the interest is compounded per year (4, since it is compounded quarterly)
t = the number of years (10)
Plugging in the values:
A = 20000(1 + 0.045/4)^(4*10)
A = 20000(1.01125)^40
A ≈ 30,708.94
The account balance after 10 years will be approximately $30,708.94.
To know more about interest, refer here:
https://brainly.com/question/20406888#
#SPJ11
suppose that a high school marching band has 108 members. of these 108 band members, 39 are seniors, 23 play the trumpet, and 8 are seniors who play the trumpet. what is the probability that a randomly selected band member is a senior given that he or she plays the trumpet? give your answer as a percentage, rounded to one decimal place.
Answers
The probability that a randomly selected band member is a senior given that he or she plays the trumpet is 34.78%.
Probability is defined as the likeliness of an event to happen. It can be calculated by dividing the total desired outcomes by the total outcomes.
P = desired outcomes / total outcomes
Of the 108 band members, if 23 play the trumpet, and 8 are seniors who play the trumpet, then the probability that a randomly selected band member is a senior given that he or she plays the trumpet is 8 divided by 23.
P = 8/23 x 100
P = 34.78%
Learn more about probability here: https://brainly.com/question/6649771
#SPJ4
*twists ankle from jumping* aCK-

Answers
Answer: second sign
Step-by-step explanation:
And what it is you’re saying if either of them are greater, less than or equal to
Since 3/8=0.375 and 1/2=0.5, it leads to 1/2 being greater to 3/8.
Consider the PDE au(x, t) = 4 d²u(x, t) 2 Ət əx² For each of BCs and ICs, solve the initial value problem. du(π,t) a) BCs: u(0,t)=0 = = 0 and əx IC: u(x,0) = x ANSWER: f(x)= n=1 u(2,t) = 0 and u(0,t)=0 u(x,0)=sin x ANSWER: f(x)=¹1_sin(2 + nx) na n=1 1+ 2 X b) BCs: IC: 8 (2n-1) T n+1 (-1)041 -4(2n-1)²t sin(2-nπ) nπ 1- 2 e sin (2n-1) 2 na sin X 2 -(nn)²t x -X
Answers
the solution for the initial value problem is: u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t) where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
The given partial differential equation is:
au(x, t) = 4 * (d²u(x, t) / dt²) / (dx²)
a) BCs (Boundary Conditions):
We have u(0, t) = 0 and u(π, t) = 0.
IC (Initial Condition):
We have u(x, 0) = x.
To solve this initial value problem, we need to find a function f(x) that satisfies the given boundary conditions and initial condition.
The solution for f(x) can be found using the method of separation of variables. Assuming u(x, t) = X(x) * T(t), we can rewrite the equation as:
X(x) * T'(t) = 4 * X''(x) * T(t) / a
Dividing both sides by X(x) * T(t) gives:
T'(t) / T(t) = 4 * X''(x) / (a * X(x))
Since the left side only depends on t and the right side only depends on x, both sides must be equal to a constant value, which we'll call -λ².
T'(t) / T(t) = -λ²
X''(x) / X(x) = -λ² * (a / 4)
Solving the first equation gives T(t) = C1 * exp(-λ² * t), where C1 is a constant.
Solving the second equation gives X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) + C3 * cos(sqrt(-λ² * (a / 4)) * x), where C2 and C3 are constants.
Now, applying the boundary conditions:
1) u(0, t) = 0:
Plugging in x = 0 into the solution X(x) gives C3 * cos(0) = 0, which implies C3 = 0.
2) u(π, t) = 0:
Plugging in x = π into the solution X(x) gives C2 * sin(sqrt(-λ² * (a / 4)) * π) = 0. To satisfy this condition, we need the sine term to be zero, which means sqrt(-λ² * (a / 4)) * π = n * π, where n is an integer. Solving for λ, we get λ = ± sqrt(-4n² / a), where n is a non-zero integer.
Now, let's find the expression for u(x, t) using the initial condition:
u(x, 0) = X(x) * T(0) = x
Plugging in t = 0 and X(x) = C2 * sin(sqrt(-λ² * (a / 4)) * x) into the equation above, we get:
C2 * sin(sqrt(-λ² * (a / 4)) * x) * C1 = x
This implies C2 * C1 = 1, so we can choose C1 = 1 and C2 = 1.
Therefore, the solution for the initial value problem is:
u(x, t) = sin(sqrt(-λ² * (a / 4)) * x) * exp(-λ² * t)
where λ = ± sqrt(-4n² / a), and n is a non-zero integer.
Note: Please double-check the provided equation and ensure the values of a and the given boundary conditions are correctly represented in the equation.
To know more about Equation related question visit:
https://brainly.com/question/29657983
#SPJ11
PLZ ANSWER THIS. I really need help from smart people.
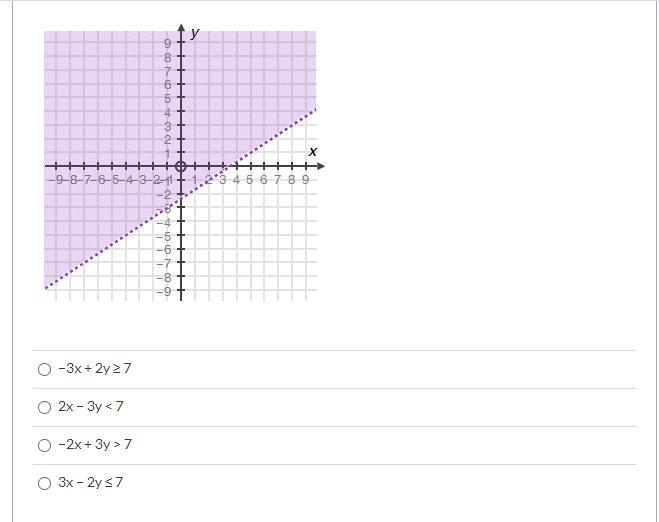
Answers
Answer:
2x-3y<7
Step-by-step explanation:
Hope it helps (:
nomas necesito la respuesta para (D)

Answers
Answer:
Tanong mo sananay mo mgaling yun
You are given a sample of metal and asked to determine its specific heat. You weigh the sample and find that its weight is $28.4 \mathrm{~N}$. You carefully add $1.25 \times 10^4 \mathrm{~J}$ of heat energy to the sample and find that its temperature rises $18.0 \mathrm{C}^{\circ}$. What is the sample's specific heat?
Answers
The specific heat of the given sample is approximately 239.6 J/(kg·°C). This value indicates the amount of heat energy required to raise the temperature of 1 kilogram of the sample by 1 degree Celsius.
To determine the specific heat of the given sample, we can use the formula Q = mcΔT, where Q is the heat energy added, m is the mass of the sample, c is the specific heat, and ΔT is the change in temperature. By rearranging the formula, we can solve for c.
In this case, we are given the heat energy Q = 1.25 × 10^4 J, the mass m = 28.4 N (weight in newtons), and the change in temperature ΔT = 18.0 °C. To calculate the specific heat c, we rearrange the formula Q = mcΔT and solve for c.
First, we convert the weight from newtons to kilograms by dividing it by the acceleration due to gravity (9.8 m/s^2). So, the mass of the sample in kilograms is 28.4 N / 9.8 m/s^2 = 2.90 kg.
Substituting the given values into the formula, we have 1.25 × 10^4 J = c × 2.90 kg × 18.0 °C. Now, we can solve for c by dividing both sides of the equation by (2.90 kg × 18.0 °C):
c = (1.25 × 10^4 J) / (2.90 kg × 18.0 °C) ≈ 239.6 J/(kg·°C).
Learn more about specific heat here:
https://brainly.com/question/31608647
#SPJ11
help me plssssssssssssssssssss

Answers
Answer: y-3
Step-by-step explanation:
because its shifted 3 units down so going down the y axis 3 spaces.
This is because every x-coordinate is shifted 1 unit to the left (negative direction), and every y-coordinate is shifted 3 units down (negative direction).
the measure of two vertical angles are 8x-18 and 6x+14 find x
A:16
B:110
C:32
D:70
18+14=32
32 divided by 2 = 16
is this right??
Answers
When the measure of two vertical angles are 8x-18 and 6x+14, x is A. 16.
How to illustrate the information?It should be noted that vertically opposite angles are equal. In this case, we have to equate both angles given. This will be illustrated as:
Angle 1 = Angle 2
8x - 18 = 6x + 14
Collect like terms
8x - 6x = 14 + 18
2x = 32
Divide
x = 32/2
x = 16
The value of x is 16.
Learn more about angles on:
brainly.com/question/25716982
#SPJ1
A rectangle has one vertex at (0, 4) on
a coordinate plane. The rectangle has
at least one side with a length of
6 units. Which vertices could represent
the other three vertices of the
rectangle?
Select all the correct answers.
A (0, -2), (-2, -2), and (-2, 4)
B (3, 4), (3, 1), and (0, 1)
(6, 4), (0, 2), and (6, 2)
D(-6, 4), (0, 5), and (-6, 5)
E (0, 6), (2, 6), and (2, 4)
Answers
The vertices that could represent the other three vertices of the rectangle are (6, 4), (0, 2), and (6, 2)
Which vertices could represent the other three vertices of the rectangle?From the question, we have the following parameters that can be used in our computation:
Vertex = (0, 4)
The rectangle has at least one side with a length of 6 units
So, we have
Possible vertices = (6, 4), (0, 2), and (6, 2)
In the above vertices, we have
Lengths = 6 units and 2 units
Hence, the vertices that could represent the other three vertices of the rectangle are (6, 4), (0, 2), and (6, 2)
Read more about rectangles at
https://brainly.com/question/24571594
#SPJ1
Let X1, X2,.....X80 be a random sample of size 80 taken from the population with p.d.f
f(x) = 3x2, 0 < x <1.
Find the mean and variance of the population and then use the Central Limit Theorem to approximate P(80). Show you work.
Answers
The sample mean of the population is 3/4 and the variance is 3/80. Using the central limit theorem, P(\(\bar{X}\) > 0.8) can be simplified as 0.003.
The mean of the population can be computed as follows:
µ = ∫x f(x) dx from 0 to 1
= ∫x (3x²) dx from 0 to 1
= 3/4
The variance of the population can be computed as follows:
σ² = ∫(x-µ)² f(x) dx from 0 to 1
= ∫(x-(3/4))² (3x²) dx from 0 to 1
= 3/80
By the Central Limit Theorem, as the sample size n = 80 is large, the distribution of the sample mean \(\bar{X}\) can be approximated by a normal distribution with mean µ and variance σ²/n.
Therefore, P(\(\bar{X}\) > 0.8) can be approximated by P(Z > (0.8-0.75)/(sqrt(3/80)/sqrt(80))), where Z is a standard normal random variable.
Simplifying, we get P(\(\bar{X}\) > 0.8) ≈ P(Z > 2.73) ≈ 0.003.
To know more about sample mean, refer here:
https://brainly.com/question/31101410#
#SPJ11
I need to find the easiest way to learn how to divide fractions
Answers
Step-by-step explanation:
to divide fractions you just flip the fraction after the divide symbol then you multiple.
e.g. \(\frac{1}{2}\)÷\(\frac{2}{3}\) = \(\frac{1}{2}\)×\(\frac{3}{2}\)..... then multiply!
Answer:
you can get chance to learn various types of fraction if you meet to your math teacher.
Step-by-step explanation:
I couldn't do because there is no system for making questions of fraction and solutions because keyboard goes give me to keep denominator.
25. (03.07 LC)Choose the equation of the vertical line passing through the point (-2, 3). (1 point)O y = 3O x = 3O y = -2O x = -2
Answers
A vertical line can be written algebraicaly in the form:
x = c
where c is a constant.
You have the point (-2,3), a vertical line which crosses this point is x = -2, because the x-coordinate of the point is x=-2.
Rachel states that -5.5 is an integer because it is negative. Is she correct. Why or why not?
Answers
Answer:
She is incorrect.
Step-by-step explanation:
She is incorrect.
An integer is a whole number, zero, and the opposites of the whole numbers. There cannot be a decimal part or fractional part to an integer.
Here are the integers:
..., -3, -2, -1, 0, 1, 2, 3, ...
-5.5 is not an integer.
Rachel's statement that -5.5 is an integer because it is negative is not correct because -5.5 is a rational number.
Given,
Rachel states that -5.5 is an integer because it is negative.
We need to find out whether Rachel's statement is correct and give a reason.
What are integers?Integers are 0,±1, ±2, ±3, ±4, ±5, ±6, ±7, ±8,......
It includes all whole numbers.
We have,
-5.5 is a negative rational number.
Integer has no decimal point.
-5.5 is not an integer.
Thus Rachel's statement that -5.5 is an integer because it is negative is not correct.
Learn more about the difference between integers and rational numbers here:
https://brainly.com/question/13212492
#SPJ2
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has:_________
Answers
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has exactly one solution.
This is because the linear function intersects the quadratic function at its minimum point, where there is only one value of x that satisfies both equations.
If a nonlinear system of equations contains one linear function that touches the quadratic function at its minimum, then the system has one unique solution.
Here's a step-by-step explanation:
1. A nonlinear system is a set of equations where at least one of the equations is not linear.
2. In this case, the nonlinear system contains one linear function and one quadratic function.
3. The quadratic function has a minimum point, which is the lowest point of its parabolic graph.
4. The linear function touches the quadratic function at its minimum, which means they intersect at exactly that point.
5. Since the two functions intersect at one point, the system has one unique solution, which corresponds to the coordinates of that intersection point.
Visit here to learn more about quadratic function:
brainly.com/question/30929439
#SPJ11
Question
The population of a certain bacteria can be modeled by the function P(t) = 2,000(1.034), where t
represents the number of hours after an experiment has started. What does 2,000 represent in the
function?
Answers
The number 2,000 represent the number of bacteria at t = 0 in the function.
What is an exponent?Consider the function:
y = a (1 ± r) ˣ
Where x is the number of times this growth/decay occurs, a = initial amount, and r = fraction by which this growth/decay occurs.
If there is a plus sign, then there is exponential growth happening by r fraction or 100r %
If there is a minus sign, then there is exponential decay happening by r fraction or 100r %
The population of a certain bacteria can be modeled by the function
\(\rm P(t) = 2,000\times (1.034) ^t\)
Where t represents the number of hours after an experiment has started.
The number 2,000 represent the number of bacteria at t = 0 in the function.
More about the exponent link is given below.
https://brainly.com/question/5497425
#SPJ1