how many cubic inches will a rectangular pyramid hold if its 15 in height by 12 inches base
Answers
The number of cubic inches that the rectangular pyramid will hold if it has 15 inches height and 12 inches base is 720 inches³.
Here we have to find the volume of the pyramid since cubic unit means the volume.
We know that,
Volume of any pyramid = 1/3 × Base area × Height
Here the given pyramid is a rectangular pyramid.
Base of the pyramid will be a rectangle.
So, base area = length × width
Now given that,
Base is 12 inches.
Since there is only a dimension, width and length will be equal to 12 inches.
So base area = 12 × 12 = 144 inches²
Height = 15 inches
Volume of the pyramid = 1/3 × 144 × 15
= 720 inches³
Hence the volume is 720 inches³.
Learn more about Volume here :
https://brainly.com/question/17615619
#SPJ1
Related Questions
The product of 4 and the difference of a number and 7.
Answers
Answer:
simplified: 4x−28
Step-by-step explanation:
The product of 4 and the difference of a number and 7 can be written as 4(x-7) where x is the number you are looking for.
What is the area of the obtuse triangle below?
I 12
1
1
21
O A. 39 sq. units
O B. 21 sq. units
O c. 126 sq.
units
O D. 252 sq. units

Answers
Answer:
C 126 sq. units
Step-by-step explanation:
A = 1/2(b)(h)
A = 1/2(21)(12)
A = 1/2 × 252
A = 126 sq. units
$18.39 is what percent of $329.64?
Answers
18.39 is 5.58% of 329.64.
We have to find that 18.39 is what percent of 120?
First, make the assumption that 329.64 is 100% as it is our output value.
We next represent the value we seek with x, therefore
100% = 329.64
And, x% = 18.39
Now, we get pair of simple equations
100% = 329.64 ........(1)
x% = 18.39 ........(2)
Now by simply dividing equation 1 by equation 2 and note of the fact that the LHS of both equations have the same unit (%);
100% / x% = 329.64 / 18.39
Taking the reciprocal of both sides, we get
x% / 100% = 18.39 / 329.64
or x = 5.58%
Hence, 18.39 is 5.58% of 329.64.
To learn more about percentages, visit: https://brainly.com/question/14319057
#SPJ9
Note: Enter your answer and show all the steps that you use to solve this problem in the space provided. You have a credit card with a balance of $754.43 at a 13.6% APR. You have $300.00 available each month to save or pay down your debts. a. How many months will it take to pay off the credit card if you only put half of the available money toward the credit card each month and make the payments at the beginning of the month? b. How many months will it take to pay off the credit card if you put all of the available money toward the credit card each month and make the payments at the beginning of the month? Be sure to include in your response: • the answer to the original question • the mathematical steps for solving the problem demonstrating mathematical reasoning
Answers
a. It will take 7 months to pay off the credit card.
b. it will take 4 months to pay off the credit card.
Since, APR stands for Annual Percentage Rate. It is the interest rate charged on a loan or credit card, expressed as a yearly percentage rate. The APR takes into account not only the interest rate, but also any fees or charges associated with the loan or credit card.
a. If you put half of the available money each month toward the credit card, then you are paying $150.00 per month towards the credit card balance.
We can use the formula for the present value of an annuity to find how many months it will take to pay off the credit card:
PV = PMT × ((1 - (1 + r)⁻ⁿ) / r)
where:
PV is the present value of the debt
PMT is the payment amount per period
r is the monthly interest rate
n is the number of periods
Substituting the values, we get:
754.43 = 150 × ((1 - (1 + 0.011333)⁻ⁿ) / 0.011333)
Simplifying and solving for n, we get:
n = log(1 + (PV ×r / PMT)) / log(1 + r)
n = log(1 + (754.43×0.011333 / 150)) / log(1 + 0.011333)
n = 6.18
Therefore, it will take 7 months to pay off the credit card if you put half of the available money each month toward the credit card.
b. If you put all of the available money each month toward the credit card, then you are paying $300.00 per month towards the credit card balance.
754.43 = 300 ×((1 - (1 + 0.011333)⁻ⁿ) / 0.011333)
Simplifying and solving for n, we get:
n = log(1 + (PV × r / PMT)) / log(1 + r)
n = log(1 + (754.43× 0.011333 / 300)) / log(1 + 0.011333)
n = 3.43
Therefore, it will take 4 months to pay off the credit card if you put all of the available money each month toward the credit card.
Learn more about APR, visit:
brainly.com/question/13597527
#SPJ1
NEED HELP 45 POINTS PLZ
Is there enough information to prove that the triangles are congruent?
If yes, provide the correct Triangle Congruence Postulate or Theorem and a congruence statement.
If no, justify your answer.
put your answer in comments plz because it will be deleted

Answers
Which of the following are point-slope equations of the line going through
(-3, 4) and (2, 1).
Answers
Answer:
-0.6x+2.2
Step-by-step explanation:
I graphed it in desmos

SOMEBODY HELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIESTHELP MATH 100 POINTS BRAINLIEST⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️ HELP MATH 100 POINTS BRAINLIEST ⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️⚠️HELP MATH 100 POINTS BRAINLIEST
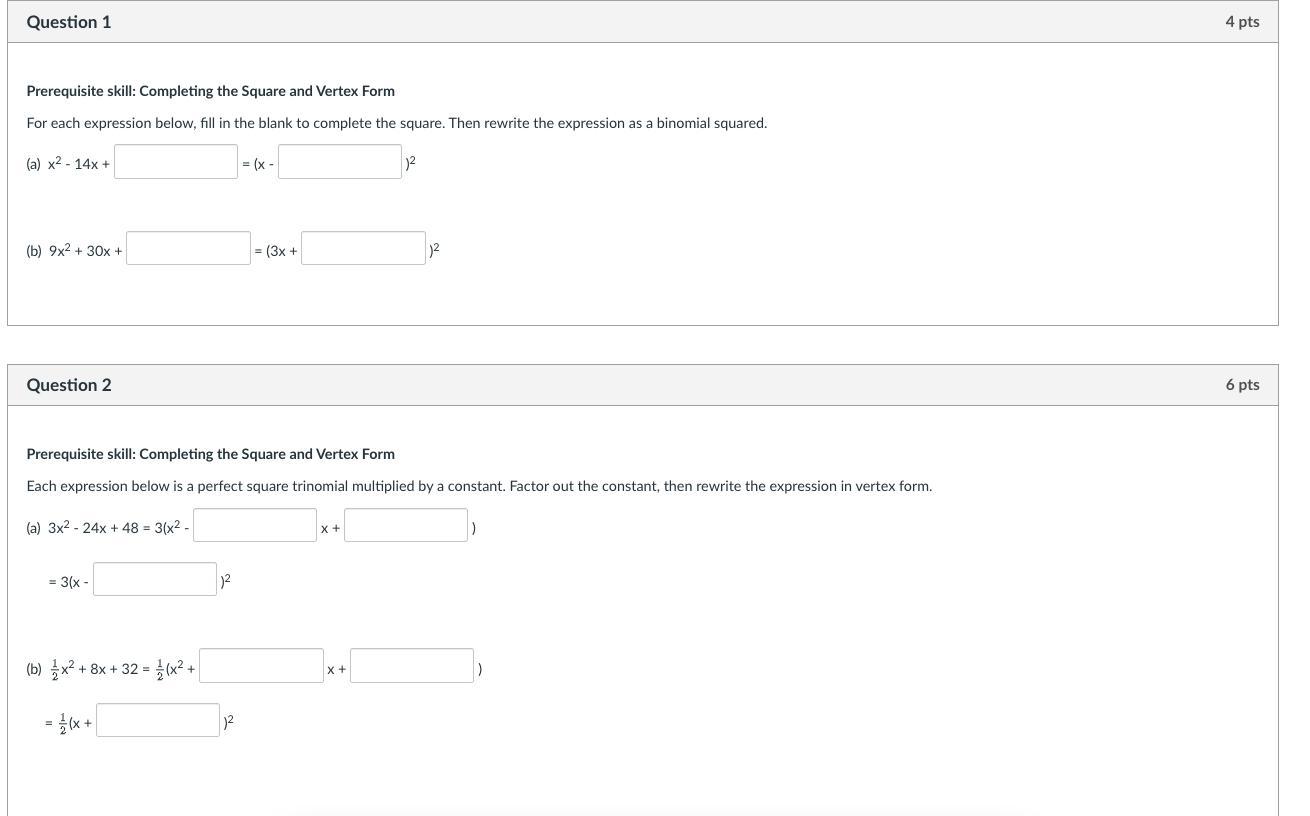
Answers
Answer:
\(\textsf{1.(a)} \quad x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
\(\textsf{1.(b)} \quad 9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\begin{aligned}\textsf{2.(a)}\quad3x^2-24x+48&=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\\&=3\left(x-\boxed{4}\right)^2\end{aligned}\)
\(\begin{aligned}\textsf{2.(b)}\quad \dfrac{1}{2}x^2+8x+32&=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\\&=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\end{aligned}\)
Step-by-step explanation:
Question 1(a) When completing the square for a quadratic equation in the form ax² + bx + c where the leading coefficient is one, we need to add the square of half the coefficient of the x-term:
\(x^2-14x+\left(\dfrac{-14}{2}\right)^2\)
\(x^2-14x+\left(-7\right)^2\)
\(x^2-14x+49\)
We have now created a perfect square trinomial in the form a² - 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Therefore:
\(a^2=x^2 \implies a=1\)
\(b^2=49=7^2\implies b = 7\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(x^2-14x+\boxed{49}=\left(x-\boxed{7}\right)^2\)
(b) When completing the square for a quadratic equation where the leading coefficient is not one, we need to add the square of the coefficient of the x-term once it is halved and divided by the leading coefficient, and then multiply it by the leading coefficient:
\(9x^2 + 30x +9\left(\dfrac{30}{2 \cdot 9}\right)^2\)
\(9x^2 + 30x +9\left(\dfrac{5}{3}\right)^2\)
\(9x^2 + 30x +9 \cdot \dfrac{25}{9}\)
\(9x^2 + 30x +25\)
We have now created a perfect square trinomial in the form a² + 2ab + b². To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 +2ab + b^2 = (a +b)^2}\)
Therefore:
\(a^2=9x^2 = (3x)^2 \implies a = 3x\)
\(b^2=25 = 5^2 \implies b = 5\)
Therefore, the perfect square trinomial rewritten as a binomial squared is:
\(9x^2 + 30x +\boxed{25}= \left(3x +\boxed{5}\right)^2\)
\(\hrulefill\)
Question 2(a) Factor out the leading coefficient 3 from the given expression:
\(3x^2-24x+48=3\left(x^2-\boxed{8}\:x+\boxed{16}\right)\)
We have now created a perfect square trinomial in the form a² - 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2 -2ab + b^2 = (a -b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=3\left(x-\boxed{4}\right)^2\)
(a) Factor out the leading coefficient 1/2 from the given expression:
\(\dfrac{1}{2}x^2+8x+32=\dfrac{1}{2}\left(x^2+\boxed{16}\:x+\boxed{64}\right)\)
We have now created a perfect square trinomial in the form a² + 2ab + b² inside the parentheses. To factor a perfect square trinomial, use the following formula:
\(\boxed{a^2+2ab + b^2 = (a +b)^2}\)
Factor the perfect square trinomial inside the parentheses:
\(=\dfrac{1}{2}\left(x+\boxed{8}\right)^2\)
Step-by-step explanation:
Since ABCD is a rectangle
⇒ AB = CD and BC = AD
x + y = 30 …………….. (i)
x – y = 14 ……………. (ii)
(i) + (ii) ⇒ 2x = 44
⇒ x = 22
Plug in x = 22 in (i)
⇒ 22 + y = 30
⇒ y = 8
Which classification best represents a triangle with side lengths 6 cm, 10 cm, and 12 cm?
acute, because 62 + 102 < 122
acute, because 6 + 10 > 12
obtuse, because 62 + 102 < 122
obtuse, because 6 + 10 > 12
Answers
Answer:
To determine the classification of a triangle based on its side lengths, we can use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the lengths of the legs (the shorter sides) is equal to the square of the length of the hypotenuse (the longest side).
For this particular triangle with side lengths 6 cm, 10 cm, and 12 cm, we can apply the Pythagorean theorem to determine whether the triangle is acute (all angles are less than 90 degrees), obtuse (one angle is greater than 90 degrees), or right (one angle is equal to 90 degrees).
Using the Pythagorean theorem, we find:
6^2 + 10^2 = 136
12^2 = 144
Since 136 is less than 144, we know that 6 cm, 10 cm, and 12 cm are the side lengths of a triangle that is obtuse (one angle is greater than 90 degrees), because the longest side (the hypotenuse) is greater than the sum of the squares of the lengths of the other two sides.
Therefore, the correct answer is: obtuse, because 6^2 + 10^2 < 12^2.
Give the slope and the y-intercept of the line y=10x+9
Answers
Answer:
Slope: 10
Y-intercept: +9
Step-by-step explanation:
An equation written in slope-intercept form is y=mx+b. "m" is your slope and b is your y-intercept.
Express 35 degrees into centesimal measure (grade, minute, second).[FULL PROCESS REQUIRED]
Answers
Answer:
sorreyyyy mateeeeee dont know the answer
I need help! 25 brainly points!

Answers
The surface areas for each figures are:
220 ft² 410 cm²596 cm²360 cm²Surface area of cylinders include: 132π mm²22π ft²396π square inches.How to calculate surface areas?1. The surface area of the cuboid is:
Top and bottom: 2(10 ft x 4 ft) = 80 ft²
Front and back: 2(10 ft x 5 ft) = 100 ft²
Sides: 2(4 ft x 5 ft) = 40 ft²
Total surface area = 80 + 100 + 40 = 220 ft²
2. The surface area of the cuboid is:
Top and bottom: 2(18 cm x 5 cm) = 180 cm²
Front and back: 2(18 cm x 5 cm) = 180 cm²
Sides: 2(5 cm x 5 cm) = 50 cm²
Total surface area = 180 + 180 + 50 = 410 cm²
3. The surface area of the prism is:
Top and bottom: 2(5 cm x 14 cm) = 140 cm²
Front and back: 2(5 cm x 12 cm) = 120 cm²
Sides: 2(12 cm x 14 cm) = 336 cm²
Total surface area = 140 + 120 + 336 = 596 cm²
4. The surface area of the stacked cuboids is:
Top and bottom of first cuboid: 2(6 cm x 7 cm) = 84 cm²
Front and back of first cuboid: 2(6 cm x 2 cm) = 12 cm²
Sides of first cuboid: 2(7 cm x 2 cm) = 28 cm²
Front and back of second cuboid: 2(7 cm x 2 cm) = 28 cm²
Sides of second cuboid: 2(2 cm x 4 cm) = 8 cm²
Front and back of third cuboid: 2(2 cm x 10 cm) = 40 cm²
Sides of third cuboid: 2(10 cm x 8 cm) = 160 cm²
Total surface area = 84 + 12 + 28 + 28 + 8 + 40 + 160 = 360 cm²
5. The surface area of the cylinder is:
Top and bottom: 2π(6 mm)² = 72π mm²
Side: 2π(6 mm)(5 mm) = 60π mm²
Total surface area = 72π + 60π = 132π mm²
6. The surface area of the cylinder is:
Top and bottom: 2π(1 ft)² = 2π ft²
Side: 2π(1 ft)(10 ft) = 20π ft²
Total surface area = 2π + 20π = 22π ft²
7. The surface area of the cylinder stacked on a cube is:
Top and bottom of cylinder: 2π(5 m)² = 50π m²
Side of cylinder: 2π(5 m)(8 m) = 80π m²
Surface area of cube: 6(10 m x 13 m) = 780 m²
Total surface area = 50π + 80π + 780 = (130π + 780) m²
8. The surface area of the cylinder is:
Top and bottom: 2π(9 in)² = 162π in²
Side: 2π(9 in)(4 in) = 72π in²
Therefore, the total surface area of the cylinder is:
2(162π in²) + 72π in² = 396π in²
So the surface area of the cylinder is 396π square inches.
Find out more on surface area here: https://brainly.com/question/16519513
#SPJ1
Image transcribed:
Find the surface area of each figure.
10 ft
18 cm
5 cm
4 ft
5 ft
3.
4.
6 cm
7 cm
2 cm
5 cm
12 cm
14 cm
4 cm
10 cm
8 cm
Find the surface area of each cylinder. Leave your answer in terms of π.
5.
6 mm
6.
1 ft
5 mm
10 ft
7.
5 m
8.
4 in.
8 m
10 m
9 in.
13 m
11 m
247
Journal and Practice Workbook
Geometry
What does 14 + 7 = ???
Guys help!!!
Ples halp!
mef neesd helpepep¡
mefnei fneafi eisafneioeale¡¡¡¡¡¡¡
Answers
Answer:
21
Step-by-step explanation:
:)
Hope this helps
PLEASE HELP I DO ANYTHING

Answers
Answer:
Step-by-step explanation: 4 if i believe
house designer uses computer-aided drawings to illustrate new houses. She likes to show her drawings to clients on a large screen. She often uses the zoom-in function to enlarge the drawings so that clients can see certain features better.
Each click of the zoom-in button results in a 10 percent increase in the size of a drawing.
(a) On a certain drawing of a house, the width of the front door is 3 inches on screen, using the default settings. Make a table of values to show the width of the door on screen after each of the first four clicks of the zoom-in button. These values should be accurate to the thousandths place.
(b) Write an algebraic rule for the function that will give the display size of the door for any number of clicks.
c) To show clients a detail on the front door, she needs to zoom in so the door is approximately 3 feet wide on screen. How many clicks of the zoom-in button will be needed to make this enlargement? Explain how you got your answer.
d) Suppose one click of the zoom-out button results in a 10 percent decrease in the size of the drawing. How many clicks of the zoom-out button would it take to transform the display of the door from 3 feet wide back to a width of approximately 3 inches?
Explain how you got your answer.


Answers
(a) Clicks Width of Door (inches)
1 3.3
2 3.63
3 3.99
4 4.39
(b) The function is y = 3 (1.1)ˣ.
(c) It would take about 15 clicks of the zoom-in button to make the door approximately 3 feet wide on the screen.
(d) It would take about 12 clicks of the zoom-out button to transform the display of the door from 3 feet wide back to a width of approximately 3 inches.
(a)
Clicks Width of Door (inches)
1 3.3
2 3.63
3 3.99
4 4.39
(b) Let x be the number of clicks and y be the width of the door on the screen. Then, we can write the algebraic rule as:
y = 3 (1.1)ˣ
(c) To make the door approximately 3 feet wide on screen, we need to convert 3 feet to inches, which is 36 inches. Then, we need to solve for x in the equation:
3 (1.1)ˣ = 36
Dividing both sides by 3, we get:
(1.1)ˣ = 12
Taking the logarithm of both sides (with base 1.1), we get:
x = log(12) / log(1.1) ≈ 14.7
So, it would take about 15 clicks of the zoom-in button to make the door approximately 3 feet wide on the screen.
(d) To transform the display of the door from 3 feet wide back to a width of approximately 3 inches, we need to find the number of clicks of the zoom-out button that will result in a width of approximately 3 inches. We can use the same formula as before, but with the initial width of 36 inches (since we are zooming out):
36 (0.9)ˣ = 3
Dividing both sides by 36, we get:
(0.9)ˣ = 1/12
Taking the logarithm of both sides (with base 0.9), we get:
x = log(1/12) / log(0.9) ≈ 11.5
So, it would take about 12 clicks of the zoom-out button to transform the display of the door from 3 feet wide back to a width of approximately 3 inches.
To learn more about the exponential function;
https://brainly.com/question/14344314
#SPJ1
John made a kite with all four sides the same length, as shown below. What is the perimeter of the kite?
Answers
Answer:
There's no images attached
The average annual cost (including tuition, room, board, books, and fees) to attend a public college takes nearly a third of the annual income of a typical family with college-age children (Money, April 2012). At private colleges, the average annual cost is equal to about 60% of the typical family's income. The following random samples show the annual cost of attending private and public colleges.
Private colleges: 52.8, 43.2, 45.0, 33.3, 44.0, 30.6, 45.8, 37.8, 50.5, 42.0.
Public colleges: 20.3, 22.0, 28.2, 15.6, 24.1, 28.5, 22.8, 25.8, 18.5, 25.6, 14.4, 21.8.
Required:
a. Based on your computation of the two sample means and the two sample standard deviations, find the degrees of freedom.
b. What is the point estimate of the difference between the two population means?
c. Develop a 95% confidence interval of the difference between the annual cost of attending private and pubic colleges.
Answers
Howard slept from 9 PM to until 6 AM the next morning. how many minutes did he sleep?
Answers
hope this helps :)
Plot each point and form the triangle ABC. Verify that the triangle ABC is a right triangle. Find its area.
A=(-2,11) B = (4.6) C=(-1,0)
Choose the correct graph below that shows points A, B, C, and triangle ABC.
D.
ОА.
Ов.
Q
a
a
To show that the triangle is a right triangle, show that the sum of the squares of the lengths of two of the sides (the legs) equals the square of the length
of the third side (the hypotenuse).
Sum of the squares of the lengths of the legs of the triangle =
Square of length of the hypotenuse of the triangle =
Find the area of the triangle.
square units
Area =
?
Click to select your answer(s).
Assignments - Goo
Take a Test - Hudso...
O
Microsoft Teams
Answers
Answer:
Step-by-step explanation:
AB=√[(4+2)²+(6-11)²]=√61
BC=√[(-1-4)²+(0-6)²]=√61
AC=√[(-1+2)²+(0-11)²]=√122
AC²=AB²+BC²
So it is a right angled triangle.

The area of the triangle is (8/5)sqrt(1199) square units.
We are given that;
Coordinates= A=(-2,11) B = (4.6) C=(-1,0)
Now,
we can plug in one point on line AB, such as A(-2, 11), and solve for b:
y = mx + b 11 = (-5/6)(-2) + b 11 = (5/3) + b b = 11 - (5/3) b = (28/3)
Hence, the equation of line AB is:
y = (-5/6)x + (28/3)
Now we can set y equal to 0 (the y-coordinate of C) and solve for x:
y = (-5/6)x + (28/3)
0 = (-5/6)x + (28/3) (-5/6)
x = -(28/3)
x = -(28/3)/(-5/6)
x = (56/15)
Therefore, point D has coordinates (56/15, 0). To find the height of the triangle, we need to find the distance between points A and D using the distance formula:
\(h = AD = sqrt((x_2 - x_1)^2 + (y_2 - y_1)^2) h = sqrt((56/15 - (-2))^2 + (0 - 11)^2) h = sqrt((136/15)^2 + 121) h = sqrt(18496/225 + 121) h = sqrt(45121/225) h = (3/15)sqrt(5024)\)
Now we can plug in the values of b and h into the area formula and simplify:
\(A = (1/2)bh A = (1/2)(sqrt(61))((3/15)sqrt(5024)) A = (1/10)sqrt(61)sqrt(5024) A = (1/10)sqrt(307584) A = (1/10)(16)sqrt(1199) A = (8/5)sqrt(1199)\)
Therefore, by the given triangle answer will be (8/5)sqrt(1199) square units.
Learn more about the triangle;
https://brainly.com/question/2773823
#SPJ2
Juliet has a choice between receiving a monthly salary of $1900 from a company or a base salary of $1800 and a 5% commission on the amount of furniture she sells during the month. For what amount of sales will the two choices be equal?
Answers
Juliet will earn the same amount of money whether she chooses a monthly salary of $1900 from the company or a base salary of $1800 plus a 5% commission on furniture sales if her sales amount to $2000.
To find the amount of sales for which the two salary choices are equal, we set the equation for the base salary plus commission equal to the equation for the flat monthly salary. The equation can be written as:
1800 + 0.05x = 1900
where x is the amount of furniture sales in dollars.
Simplifying and solving for x, we get:
0.05x = 100
x = 2000
If she sells less than $2000 of furniture, she will earn more with the flat monthly salary of $1900. If she sells more than $2000 of furniture, she will earn more with the base salary plus commission. This calculation provides an important decision-making tool for Juliet, as she can tailor her salary choice based on her expected sales for the month.
For such more questions on amount
https://brainly.com/question/24644930
#SPJ8
A waterfall has a height of 1900 feet. A pebble is thrown upward from the top of the falls with an initial velocity of 12 feet per second. The height, h, of the pebble after t seconds is given by the equation h=-16t^2+12t+1900. How long after the pebble is thrown will it hit the ground?
Answers
Answer:
Step-by-step explanation:
h is the height of the pebble after a certain amount of time has gone by. Since we are told to find that time when the pebble is on the ground, we say that h = 0 since the height of something on the ground has no height at all. Then factor the quadratic.
\(-16t^2+12t+1900=0\)
Throw that into the quadratic formula or however you were taught to factor irrational quadratics (maybe completing the square?) to get that
t = 11.27869 sec and t = -10.52869 sec
Since we all know that time will never carry a negative value, we will disregard it and go with 11.27869 seconds. Not sure to where you are told to round.
In Rebecca's neighborhood, 89% of the houses have garages and 48% have a
garage and a pool. What is the probability (in percent) that a house in her
neighborhood has a pool, given that it has a garage? Round your answer to 1
decimal place.
Answers
why are there two of these?
Answer:
53.9
Step-by-step explanation:
89% of all houses have garages and 48% have garages and pools. We try to find houses with a pool that have a garage. Let's assume that there are 100 houses in her neighborhood. then 89 of them have garages and 48 of them have garages and pools. 48 / 89 = about 0.5393. Conver this to percent and we get 53.9
7x2x2x2 is the prime factorization for which of the following
А
72
B
56
С
44
D
28
Answers
Just multiply all numbers and see which number from the choices match your answers after doing the multiplication! Hope I helped!
Age of Senators The average age of senators in the 108th Congress was 56.5 years. If the standard deviation was 12.5 years, find the Z-scores corresponding to the oldest and youngest senators of age 85 and 39. Round z scores to two decimal places. Part: 0/2 Part 1 of 2 The Z-score corresponding to the oldest senator of age 85 is oll
Answers
Rounding to two decimal places, the Z-score corresponding to the youngest senator of age 39 is -1.40.
To find the Z-score corresponding to a particular value in a normal distribution, we use the formula:
Z = (x - μ) / σ
where x is the value of interest, μ is the mean, and σ is the standard deviation.
Part 1 of 2: For the oldest senator of age 85:
Z = (x - μ) / σ = (85 - 56.5) / 12.5 ≈ 2.28
Rounding to two decimal places, the Z-score corresponding to the oldest senator of age 85 is 2.28.
Part 2 of 2: For the youngest senator of age 39:
Z = (x - μ) / σ = (39 - 56.5) / 12.5 ≈ -1.4
Rounding to two decimal places, the Z-score corresponding to the youngest senator of age 39 is -1.40.
Learn more about standard deviation here :
brainly.com/question/29991053
#SPJ4
find the absolute valve of 1 1/2 - 2/31
Answers
Answer: To find the absolute value of the expression 1 1/2 - 2/31, we first need to convert the mixed number 1 1/2 into an improper fraction.
1 1/2 can be written as (2 * 1 + 1) / 2, which is equal to 3/2.
Now we can subtract 2/31 from 3/2:
3/2 - 2/31 = (3 * 31 - 2 * 2) / (2 * 31) = (93 - 4) / 62 = 89/62.
The absolute value of a fraction is the positive value without considering its sign. So, the absolute value of 89/62 is 89/62.
Therefore, the absolute value of 1 1/2 - 2/31 is 89/62.
Please answer this!
Who invented maths?
Answers
Answer:
ancient greek invented math
Kayla bought a new leather jacket for $139.99, with 8.625% sales tax, write the equation for the purchase and justify the value of j.
Answers
Answer:
j = 139.99 + 139.99 * 0.08625
Answer:
Step-by-step explanation:
A blogger had 400 subscribers to her blog in January. The number of subscribers has grown by a factor of 1.5 every month since then. Write a sequence to represent the number of subscribers in the 3 months that followed.
Answers
Answer:
\(600, 900, 1350\)
Step-by-step explanation:
Given
\(a = 400\) -- initial subscribers
\(b = 1.5\) -- growth factor
Required
Determine the number of subscribers in the next three months
To do this, we make use of:
\(y = ab^x\)
In this case:
x is the number of months
y is the number of subscribers
So:
when x = 1;
\(y = ab^x\)
\(y = 400 * 1.5^1\)
\(y = 400 * 1.5\)
\(y = 600\)
when x = 2
\(y = 400 * 1.5^2\)
\(y = 400 * 2.25\)
\(y = 900\)
when x= 3
\(y = 400 * 1.5^3\)
\(y = 400 * 3.375\)
\(y = 1350\)
So, the next three number of subscribers is:
\(600, 900, 1350\)
HELPPPPPPP ASAPPPPPPPPPPP
What is the height of the cannon before it is launched, at t=0? Remember to include units.
A projectile’s maximum height is shown by the vertex of the parabola. When does the cannonball reach its maximum height? Round to the nearest whole number and remember to include units.
What is the maximum height of the cannonball? Round to the nearest whole number and remember to include units.
How long does it take the cannonball to land on the ground? Round your answer to the nearest whole number and remember to include your units.
If you launch the cannonball from the ground instead (hi=0), what does that change in the original equation?
What would be the equation of the cannonball’s path if it was launched with the same velocity, but from the ground instead?
Using this new equation, what is the new maximum height of the ball and how long did it take to hit the ground? Round to the nearest whole number and remember to include units.

Answers
Since t = 0 corresponds to the initial launch, the cannonball hits the ground after 4 seconds.
What is equation?An equation is a mathematical statement that shows the equality between two expressions, often with one or more variables. It consists of two sides separated by an equal sign. An equation may have one or more solutions, which are values of the variables that make both sides of the equation equal. Equations are commonly used in many branches of mathematics, as well as in physics, engineering, and other sciences, to model relationships between quantities and to solve problems.
Here,
To find the height of the cannon before it is launched, we can look at the equation h(t) = −4.9t² + 19.8t + 58 and plug in t=0:
h(0) = −4.9(0)² + 19.8(0) + 58
= 58 meters
To find when the cannonball reaches its maximum height, we can use the formula for the x-coordinate of the vertex of a parabola:
x = -b/2a, where a=-4.9 and b=19.8.
Plugging in these values, we get x = -19.8/(2*(-4.9))
= 2.02 seconds
To find the maximum height of the cannonball, we can plug in the value of t we just found (t=2.02 seconds) into the original equation and solve for h:
h(2.02) = −4.9(2.02)² + 19.8(2.02) + 58
≈ 65 meters
To find how long it takes the cannonball to land on the ground, we can look at the equation h(t) = −4.9t² + 19.8t + 58 and set h(t) = 0 (since the cannonball hits the ground when its height is 0):
−4.9t² + 19.8t + 58 = 0
Solving for t using the quadratic formula, we get t ≈ 4 seconds.
If we launch the cannonball from the ground instead (hi=0), the initial height term in the equation disappears and we get:
h(t) = −4.9t² + 19.8t
To find the new equation of the cannonball's path if launched from the ground, we simply remove the initial height term hi from the original equation:
h(t) = −4.9t² + 19.8t
To find the new maximum height of the ball and how long it takes to hit the ground, we can use the same methods as before, but with the new equation.
The x-coordinate of the vertex is x = -b/2a
= -19.8/(2*(-4.9))
= 2.02 seconds.
Plugging this into the new equation, we get:
h(2.02) = −4.9(2.02)² + 19.8(2.02)
≈ 64 meters
To find the time it takes to hit the ground, we set h(t) = 0 and solve for t: −4.9t² + 19.8t = 0, which gives t = 0 or t = 4 seconds (the same as before).
However, since we know the cannonball was launched from the ground, we can ignore the solution t=0, and conclude that the cannonball hits the ground after approximately 4 seconds.
To know more about equation,
https://brainly.com/question/28243079
#SPJ1
-1/4 plus 3/5
Answer or else
Answers
The algebric expression -1/4 + 3/5 is equal to 7/20 when simplified.
To solve the expression -1/4 + 3/5, we need to find a common denominator for the fractions and then perform the addition.
The common denominator for 4 and 5 is 20. We can rewrite the fractions with this denominator:
-1/4 = -5/20
3/5 = 12/20
Now that the fractions have the same denominator, we can add them:
-5/20 + 12/20 = (-5 + 12)/20 = 7/20
Therefore, -1/4 + 3/5 is equal to 7/20.
To further simplify the fraction, we can check if there is a common factor between the numerator and denominator. In this case, 7 and 20 have no common factors other than 1, so the fraction is already in its simplest form.
Thus, the final answer is 7/20.
For more such question on algebric expression. visit :
https://brainly.com/question/4344214
#SPJ8
solve for x, using the secant lines. 53° 189°
Answers
The measure of the arc opposite to 189° is 136°.
What are secant lines?Secant lines are lines that intersect a curve at two distinct points. They are used to approximate the slope of the curve by measuring the change in the y-coordinate of the two points divided by the change in the x-coordinate of the two points.
The measure of the angle opposite to 189° is x.
To solve for x, we can use the property of alternate interior angles.
The sides of the two secant lines that intersect outside the circle form alternate interior angles whose measures are equal.
Therefore, the two angles formed by the secant lines inside the circle must have the same measure.
Therefore, 53° + x° = 189°.
Subtracting 53° from both sides, we get x° = 136°.
For more questions related to arc
https://brainly.com/question/29860198
#SPJ1
