How i can answer this question, NO LINKS, if you answer correctly i will give u brainliest!

Answers
Answer:
Step-by-step explanation:
x^2.x^1
=9^2.9^1
= 9 multiplied by 9
=81
9 multiplied by 1
=9
81 multiplied by nine
=585.198599
Related Questions
when the factors of a trinomial are (x-p) and (x+q) then the constant term of the trinomial is: A. The product of -p and qB. The quotient of -p and q C. The sum of -p and q D. The difference -p and q

Answers
In this problem, we want to determine which variables will give us the constant term of the trinomial.
We are given the binomials
\((x-p)(x+q)\)When mutliplying these binomials, we can use the distributive property, or we can use the FOIL method.
Using distribution, we get:
\(x(x+q)-p(x+q)\)Distributing the x and p for each term, we have
\(x^2+qx-px-pq\)Recall that a constant term is any number that does not have a variable "attached" to it. For example, these are constants:
\(4,6,7...\)However, this is an abstract example. So for our purposes, the only true variable will be x, while p and q represent some unknown real numbers.
Since x is our variable, we see only the last term has no x attached to it.
\(x^2+qx-px-\boxed{pq}\)Therefore, the constant term of the trinomial is the product of -p and q.
You are going to deposit $2,500 in an account that pays .51 percent interest compounded quarterly. How much will you have in 5 years?
$2,770.82
$2,753.70
$2,767.74
$2,781.86
$2,765.62
Answers
The amount you will have in 5 years with an initial deposit of $2,500 in an account that pays .51 percent interest compounded quarterly is $2,767.74.
To calculate the interest earned for the next 5 years at a quarterly compounding rate of .51 percent, we use the formula given below;A = P(1 + r/n)^(nt)
where, A is the amount,P is the principal, r is the interest rate in decimal, n is the number of times compounded per year and t is the number of years we will invest in.
Using the formula, we can get the answer. Therefore, the amount you will have in 5 years with an initial deposit of $2,500 in an account that pays .51 percent interest compounded quarterly is $2,767.74.
Learn more about investment at
https://brainly.com/question/27949667
#SPJ11
Which of the following is the parent function of all absolute value functions?
f(x) = 3x
f(x) = |x|
f(x) = 2|x|
f(x)= x^2
Answers
Answer:
(B.) f(x) = |x|
Step-by-step explanation:
Just took the test%
Elimination was used to solve a system of equations.
One of the intermediate steps led to the equation 9x = 27.
Which of the following systems could have led to this equation?
O
9x + 2y = 21
-9x - 2y = 21
10x - y = 15
x+y = - 12
7x - 2y = 15
x + y = 6
4x + 3y = 24
-5x - 3y = 3
Answers
The system of equation that could have led to the equation 9x = 27 is
7x - 2y = 15
x + y = 6
The correct option is the third option
7x - 2y = 15
x + y = 6
Solving systems of equationsFrom the question, we are to determine the system that could have led to 9x = 27
1.
9x + 2y = 21
-9x - 2y = 21
Subtracting, we get
9x + 2y = 21
-9x - 2y = 21
-------------------
18x + 4y = 0
2.
10x - y = 15
x + y = - 12
Subtracting, we get
10x - y = 15
x + y = - 12
---------------------
9x -2y = 27
3.
7x - 2y = 15
x + y = 6
Here, multiply the second equation by 2
2 × [x + y = 6]
2x + 2y = 12
Now, add to the first equation
7x - 2y = 15
2x + 2y = 12
------------------
9x = 27
4.
4x + 3y = 24
-5x - 3y = 3
Subtracting, we get
4x + 3y = 24
-5x - 3y = 3
---------------------
9x + 6y = 21
Hence, the system of equation that could have led to the equation 9x = 27 is
7x - 2y = 15
x + y = 6
The correct option is the third option
7x - 2y = 15
x + y = 6
Learn more on Systems of equations here: https://brainly.com/question/12691830
#SPJ1
F(x)=12, then x=
I need it
Answers
Select the correct answer from each drop-down menu.
Consider quadrilateral EFGH on the coordinate grid.
-6
E
-4
1
LL
F
>+
Y
6-
2-
O
-4-
-6-
H
-N
G
05.
6
In quadrilateral EFGH, sides FG and EH are
are
X
because they
The area of quadrilateral EFGH is closest to
✓square units.
Sides EF and GH
First box ( not congruent, congruent).
Second box ( each have a length of 5.83, each have a length of 7.07, have different lengths)
Third box ( not congruent, congruent with lengths of 4.24, congruent with length of 5.83)
Fourth box (41, 34, 25, 30)

Answers
In quadrilateral EFGH, sides FG and EH are congruent because they each have a length of 7.07. Sides EF and GH are not congruent. The area of quadrilateral EFGH is closest to 41 square units.
How to calculate the distance between the two points?For the width, we would determine the distance between the vertices F (-1, 4) and G(4, -1)
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance FG = √[(4 - (-1))² + (-1 - 4)²]
Distance FG = √[5² + (-5)²]
Distance FG = √50
Distance FG = 7.07 units.
Distance EH = √[(1 - (-4))² + (-4 - 1)²]
Distance EH = √[5² + (-5)²]
Distance EH = √50
Distance FG = 7.07 units.
For the length, we would determine the distance between the vertices E (-4, 1) and F (-1, 4)
Distance = √[(x₂ - x₁)² + (y₂ - y₁)²]
Distance EF = √[(-1 - (-4))² + (4 - 1)²]
Distance EF = √[3² + (3)²]
Distance EF = √9
Distance EF = 3 units.
Distance HG = √[(4 - 1)² + (1 - (-4))²]
Distance HG = √[3² + (5)²]
Distance HG = √34 units.
Mathematically, the area of a rectangle can be calculated by using this formula:
Area of rectangle = length × width
Area of rectangle = √34 × 7.07
Area of rectangle = 41.22 square units.
Read more on area of a rectangle here: brainly.com/question/25292087
#SPJ1
NEED HELP ASAP PLEASE

Answers
Answer:
729
Step-by-step explanation:
9x9x9 = 729 in^3
I have been trying to find the answer for 10 minutes now..Please help!

Answers
Plugging in the values, we see that object 1 has more potential energy (the ball to the left)
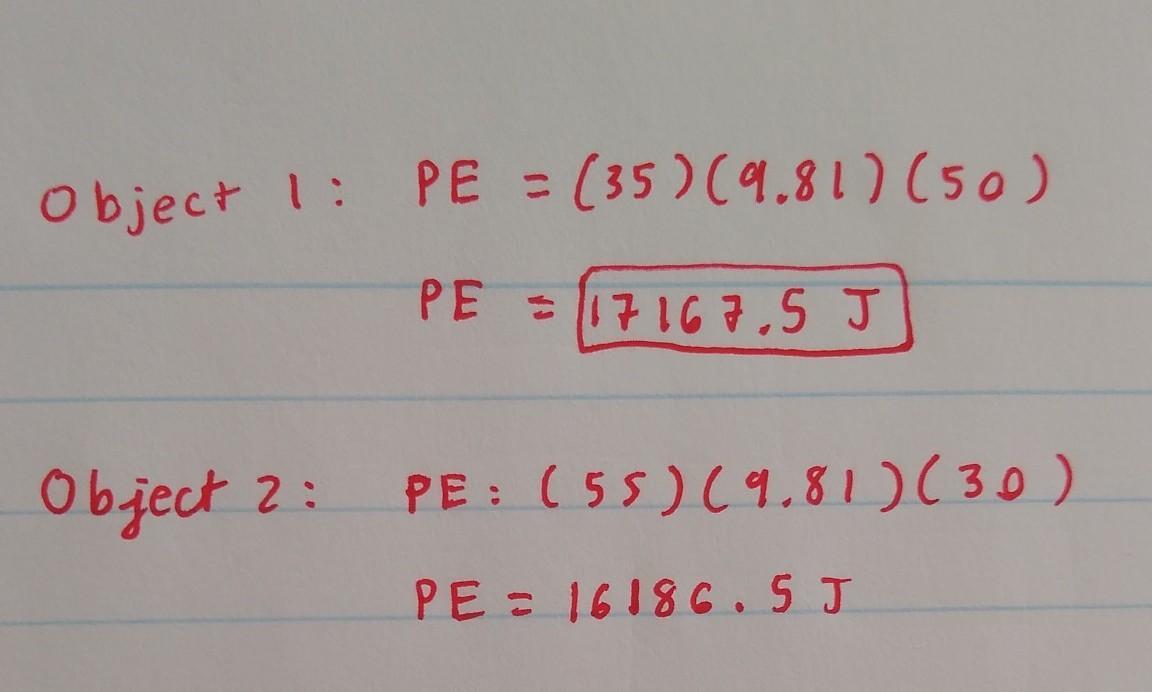
right triangle trigonometry
please help!

Answers
Answer:
AB = 9.06
Step-by-step explanation:
Side AB is adjacent to angle B, To calculate it, the cosine trig ratio is used:
\(cos39^{o} =\frac{AB}{11.66}\)
\(AB=11.66cos39^{o} =9.06\)
Hope this helps
ahhhh if someone can please help!!

Answers
Answer and Step-by-step explanation:
The y-intercept is (0, 3)
The value 3 is in the y place.
#teamtrees #WAP (Water And Plant)
A parallelogram has area of 65 square units and a height of 5. Find its base. II
Answers
Answer: 13
Step-by-step explanation:
For questions 19-27, use the ellipse defined by the following equation: 2(x+4)^2+3(y-1)^2=24.
19. write the equation of the ellipse in standard form.
20. What are the coordinates of the center?
21. What is the length of the major axis?
22. What is the length of the minor axis?
23. What is the sum of the focal radii?
24.What are the coordinates of the foci?
25. What are the coordinates of the vertices?
26. Find the eccentricity of the ellipse.
27. Draw a sketch of the ellipse.
PLEASE SHOW WORK!!
Answers
Answer:
\(\textsf{19.} \quad \dfrac{(x+4)^2}{12}+\dfrac{(y-1)^2}{8}=1\)
\(\textsf{20.} \quad \textsf{Center}: \;\;(-4, 1)\)
\(\textsf{21.} \quad \textsf{Major axis}:\;\;4\sqrt{3}\)
\(\textsf{22.} \quad \textsf{Minor axis}:\;\;4\sqrt{2}\)
\(\textsf{23.} \quad \textsf{Sum of the focal radii}:\;\;4 \sqrt{3}\)
\(\textsf{24.} \quad \textsf{Foci}:\;\;(-6, 1)\;\; \textsf{and}\;\;(-2,1)\)
\(\begin{aligned}\textsf{25.} \quad &\textsf{Vertices}:\;\;(-4-2\sqrt{3}, 1) \;\; \textsf{and}\;\; (-4+2\sqrt{3}, 1)\\ &\textsf{Co-vertices}:\;\;(-4, 1-2\sqrt{2}) \;\; \textsf{and}\;\; (-4, 1+2\sqrt{2})\end{aligned}\)
\(\textsf{26.} \quad \textsf{Eccentricity}\;\;\dfrac{\sqrt{3}}{3}\)
27. See attachment.
Step-by-step explanation:
\(\boxed{\begin{minipage}{5 cm}\underline{General equation of an ellipse}\\\\$\dfrac{(x-h)^2}{a^2}+\dfrac{(y-k)^2}{b^2}=1$\\\end{minipage}}\)
Given equation:
\(2(x+4)^2+3(y-1)^2=24\)
To write the equation of the ellipse in standard form, divide both sides by 24 so that the right side of the equation is equal to one:
\(\implies \dfrac{2(x+4)^2}{24}+\dfrac{3(y-1)^2}{24}=\dfrac{24}{24}\)
\(\implies \dfrac{(x+4)^2}{12}+\dfrac{(y-1)^2}{8}=1\)
Therefore:
\(h = -4\)\(k = 1\)\(a^2 = 12 \implies a=2\sqrt{3}\)\(b^2 = 8 \implies b=2 \sqrt{2}\)The center of the ellipse is (h, k).
Therefore, the coordinates of the center are (-4, 1).
As a > b, the ellipse is horizontal, so 2a is the major axis and 2b is the minor axis. Therefore:
Major axis = 2 × 2√3 = 4√3Minor axis = 2 × 2√2 = 4√2The focal radius is the distance from a point on the ellipse to a focus.
The sum of the focal radii is equal to the length of the major axis.
Therefore, the sum of the focal radii is 4√3.
As a > b, the coordinates of the foci are (h±c, k).
As c² = a² - b², first find the value of c:
\(\implies c^2=12-8\)
\(\implies c=\sqrt{4}=2\)
Therefore, the coordinates of the foci are:
(-4+2, 1) = (-2, 1)(-4-2, 1) = (-6, 1)As a > b, the coordinates of the vertices are (h±a, k):
(-4-2√3, 1) and (-4+2√3, 1)and the coordinates of the co-vertices are (h, k±b):
(-4, 1-2√2) and (-4, 1+2√2)The eccentricity of the ellipse is:
\(\implies e=\dfrac{c}{a}=\dfrac{2}{2\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)

by including another variable in the regression, you could group of answer choices decrease the regression r2 if that variable is important. decrease the variance of the estimator of the coefficients of interest. eliminate the possibility of omitted variable bias from excluding that variable. look at the t-statistical of the coefficient of that variable and include the variable only if the coefficient is statistically significant at the 1% level.
Answers
Careful consideration and statistical analysis should be undertaken to determine the appropriate variables to include in a regression model.
By including another variable in a regression analysis, several outcomes are possible. Let's consider the statements you provided one by one:
1. Decrease the regression R^2 if that variable is important:
- If the added variable is important and has a meaningful relationship with the dependent variable, it can increase the explanatory power of the regression model, thereby increasing the R^2.
However, if the added variable is not relevant or has a weak relationship with the dependent variable, it can decrease the R^2.
2. Decrease the variance of the estimator of the coefficients of interest:
- Including additional variables in a regression model can sometimes help to reduce the variance of the coefficient estimators for the variables of interest.
This is because including more relevant variables can help to explain some of the variance in the dependent variable, leaving less unexplained variance for the coefficients of interest.
3. Eliminate the possibility of omitted variable bias from excluding that variable:
- Omitted variable bias can occur when an important variable is not included in the regression model.
Including all relevant variables in the model can help reduce the risk of omitted variable bias, as it allows for a more comprehensive analysis of the relationship between the dependent variable and the independent variables.
4. Look at the t-statistic of the coefficient of that variable and include the variable only if the coefficient is statistically significant at the 1% level:
- The t-statistic measures the statistical significance of a coefficient. Inclusion of a variable in a regression model is often based on its statistical significance.
If the coefficient of the variable is statistically significant at the desired significance level (e.g., 1%), it suggests that the variable has a meaningful impact on the dependent variable and can be included in the model.
It is important to note that the effect of including an additional variable in a regression model depends on various factors such as the relationship between the variables, sample size, multicollinearity, and the specific research context.
Therefore, careful consideration and statistical analysis should be undertaken to determine the appropriate variables to include in a regression model.
To know more about variables refer here:
https://brainly.com/question/15078630#
#SPJ11
Look at photo for question ?

Answers
Answer:
1/3n - 3<6
n < 27
Step-by-step explanation:
1/3n - 3<6
Add 3 to each side
1/3n -3+3<6+3
1/3 n <9
Multiply by 3
1/3n *3 < 9*3
n < 27
So what can we do with this

Answers
Answer:
(-5, -3)
Step-by-step explanation:
Divide by 2
Suppose X has an exponential distribution with parameter λ=1. Let Y=e^−X.Find the probability density function of Y.
Answers
The probability density function of Y is f_Y(y) = 1, for y ∈ (0, 1).
Given that X has an exponential distribution with λ=1.
Let X be a random variable with an exponential distribution characterized by parameter λ=1. This implies that the probability density function of X is given by:
f_X(x) = λ * e^(-λx) = e^(-x), for x ≥ 0.
Now, we are asked to find the probability density function of Y, where Y = e^(-X). To do this, we'll use the transformation technique. First, we find the inverse transformation X = g(Y) by solving for X:
X = -ln(Y)
Next, we compute the derivative of g(Y) with respect to Y:
dg(Y)/dY = -1/Y
Now, we can use the transformation technique formula to find the pdf of Y:
f_Y(y) = f_X(g(y)) * |dg(y)/dy| = e^(-(-ln(y))) * |-1/y|
Simplifying this expression, we get:
f_Y(y) = y * (1/y) = 1, for y in the range (0, 1).
So, the probability density function of Y is f_Y(y) = 1, for y ∈ (0, 1).
To know more about probability density function, refer to the link below:
https://brainly.com/question/31040390#
#SPJ11
4.5 ×10⁵ as an ordinary number
Answers
The required, 4.5 × 10⁵ as an ordinary number is 450,000.
An ordinary number is a number that is expressed in the usual way, using digits 0-9 without any exponent notation or other mathematical symbols.
4.5 × 10⁵ means 4.5 multiplied by 10 raised to the power of 5. To write this as an ordinary number, we simply need to perform this multiplication:
4.5 × 10⁵ = 4.5 × 100,000 = 450,000
Therefore, 4.5 × 10⁵ as an ordinary number is 450,000.
Learn more about ordinary numbers here:
https://brainly.com/question/7244720
#SPJ1
Find the best linear approximation, L(x), to f(x) = e' near x = 0. i.L(x) = x+1 ii. L(x) = x iii. LX) = c + 1
Answers
The best linear approximation to the function f(x) = e^x near x = 0 is L(x) = x + 1.
The given function is f(x) = e^x near x = 0.
To find the best linear approximation, L(x), we use the formula:
L(x) = f(a) + f'(a)(x-a),
where a is the point near which we are approximating.
Let a = 0, so that a is near the point x = 0.
f(a) = f(0) = e^0 = 1
f'(x) = d/dx (e^x) = e^x;
so f'(a) = f'(0) = e^0 = 1
Substituting these values into the formula: L(x) = 1 + 1(x-0) = x + 1
Therefore, the best linear approximation to f(x) = e^x near x = 0 is L(x) = x + 1.
For instance, linear approximation is used to approximate the change in a physical quantity due to a small change in another quantity that affects it.
To know more about linear approximation, visit:
https://brainly.com/question/1621850
#SPJ11
PLEASE HELP!! Due very soon!!! - The graph below represents the height of a football pass, in feet, x seconds after the ball is thrown. Which of the following best describes the interpretation of f(2)? (Attached are the multiple choice answers)

Answers
Answer:
The ball is 7 feet above the ground 2 seconds after it is thrown.
Step-by-step explanation:
As per the given statement, we are given a graph of function \(f(x)\) where 'x' is time (in seconds) in the current scenario.
Time is plotted on x axis and height of football is plotted on y axis.
\(f(x)\) is the height of football according to change in time.
Following are the few things that can be observed from the given curve:
1. Initial Height of football is ~4.8 feet i.e. at 0 seconds of time.
2. Football reaches a maximum height of ~7.2 feet at 1.5 seconds.
3. After 1.5 seconds, the height of football starts decreasing.
Here f(2) means, the height of ball at 2 seconds of time.
It is clearly visible from the given graph that height is 7 feet at 2 seconds.
Please refer to the attached answer image. Height at 2 seconds is marked as point P.
Hence, The ball is 7 feet above the ground 2 seconds after it is thrown.

Abcd is a rectangle.

Answers
How many of the positive integer factors of 15552 are perfect squares? (WILL MARK BRAINLIEST IF CORRECT)
Answers
15552|2
7776|2
3888|2
1944|2
972|2
486|2
243|3
81|3
27|3
9|3
3|3
1
\(15552=2^6\cdot 3^5=(2^3\cdot3^2)^2\cdot 3\)
\((3+1)\cdot(2+1)=4\cdot 3=12\)
It's 12
Help no links please

Answers
(a) Find the sum of the first 200 natural numbers. (b) A golfball is dropped from a height of 30ft to the pavement. It always rebounds three fourths of the distance that it drops. How far (up and down) will the ball have traveled when it hits the pavement for the 6th time? (5)
Answers
a. the sum of the first 200 natural numbers is 20,100. b. when the ball hits the pavement for the 6th time, it will have traveled approximately 104 feet in total (up and down).
(a) To find the sum of the first 200 natural numbers, we can use the formula for the sum of an arithmetic series.
The sum of the first n natural numbers is given by the formula: Sn = (n/2)(a + l), where Sn represents the sum, n is the number of terms, a is the first term, and l is the last term.
In this case, we want to find the sum of the first 200 natural numbers, so n = 200, a = 1 (the first natural number), and l = 200 (the last natural number).
Substituting these values into the formula, we have:
Sn = (200/2)(1 + 200)
= 100(201)
= 20,100
Therefore, the sum of the first 200 natural numbers is 20,100.
(b) The ball rebounds three-fourths of the distance it drops, so each time it hits the pavement, it travels a total distance of 1 + (3/4) = 1.75 times the distance it dropped.
For the 6th rebound, we need to find the distance the ball traveled when it hits the pavement.
Let's represent the initial drop distance as h (30 ft).
The total distance traveled after the 6th rebound is given by the sum of a geometric series:
Distance = h + h(3/4) + h(3/4)^2 + h(3/4)^3 + ... + h(3/4)^5 + h(3/4)^6
Using the formula for the sum of a geometric series, we can simplify this expression:
Distance = h * (1 - (3/4)^7) / (1 - 3/4)
Simplifying further:
Distance = h * (1 - (3/4)^7) / (1/4)
= 4h * (1 - (3/4)^7)
= 4 * 30 * (1 - (3/4)^7)
Calculating the value:
Distance ≈ 4 * 30 * (1 - 0.1335)
≈ 4 * 30 * 0.8665
≈ 104 ft
Therefore, when the ball hits the pavement for the 6th time, it will have traveled approximately 104 feet in total (up and down).
Learn more about natural numbers here
https://brainly.com/question/2228445
#SPJ11
Are repeating decimals like 34.79 rational numbers?
Answers
Answer:
Yes. 34.79 is a rational number because it can be written as a fraction.
Step-by-step explanation:
Hoped this helped.
You have just received your first paycheck of $4,400 from your new job. You visit the dealership with your friend in search of a car. You see a a used car for $4000. The manager tell you that he will give you a discount of 50 percent. When you get home, your parents tell you that they will pay 50 % of the remaining balance.
You are excited when your friend tell you that you will get the car for "free". You will not have to pay any of your own money for the car?
Answer the questions below by showing your work for each question. Answer must be in full sentence.
a) Is your friend correct in assuming that you will not have to pay any of your own money for the car? Why or why not. Proof it.
b) How much if any of your own money will you have to pay for the car?
Skip to navigation
Pls help me
Answers
Answer: see below...
Step-by-step explanation:
a) no: 50% of 4,000 is 2,000. 50% of 2,000 is a 1,000. So the car is not “free”, you will have to pay a $1,000.
b) $1,000
A helicopter is descending from an altitude of 1,500 feet. The helicopter descends at a constant rate of 280 feet per minute. Which function can be used to determine H, the height of the helicopter above the ground after m, minutes? A H=280m+1,500H=280m+1,500H=280m+1,500 B H=1,500−280mH=1,500-280mH=1,500−280m C H=1,500m+280H=1,500m+280H=1,500m+280 D H=280m−1,500H=280m-1,500H=280m−1,500
Answers
The function that can be used to get the height of the helicopter above the ground is: H=280m−1,500
What is a function in mathematics?A function is a statement, rule, or law in mathematics that establishes the link between an independent variable and a dependent variable (the dependent variable).
How to solve for the function
The value 280 is the constant rate that the helicopter is said to be descending.
The altitude from which it is coming down is given as 1500 feet
The function would be written as H=280m−1,500
Read more on functions here: https://brainly.com/question/10439235
#SPJ1
find all the asymtotes. explain how you got to your answer very
clearly. refer to the example photo of how to properly answer the
questions
Find all of the asymptotes, both vertical and horizontal, for the function g(x) = and be certain to explain your answers. 22 + 5x + 4 3.x2 +r-2 In. 'ind all of the vertical asymptotes for the function
Answers
The horizontal asymptote of the function is y = 0.
The function g(x) has two vertical asymptotes, one at\(x = (-r + \sqrt (r^2 + 24))/6\) and the other at \(x = (-r - \sqrt(r^2 + 24))/6\), and a horizontal asymptote at y = 0.
The asymptotes of a function, we need to determine when the function is undefined.
Vertical asymptotes occur when the denominator of a fraction is equal to zero, while horizontal asymptotes occur when the value of the function approaches a constant as x approaches infinity or negative infinity.
Starting with the given function \(g(x) = (22 + 5x + 4)/(3x^2 + r - 2)\), we can find the vertical asymptotes by setting the denominator equal to zero and solving for x:
\(3x^2 + r - 2 = 0\)
This is a quadratic equation, and we can solve for x using the quadratic formula:
\(x = (-r \± \sqrt (r^2 + 24))/6\)
Since we don't know the value of r, we cannot determine the exact values of the vertical asymptotes.
We can say that there are two vertical asymptotes, one at \(x = (-r + \sqrt (r^2 + 24))/6\)and the other at\(x = (-r - \sqrt (r^2 + 24))/6\).
To find the horizontal asymptotes, we need to look at the behavior of the function as x approaches infinity and negative infinity.
We can do this by dividing both the numerator and denominator by the highest power of x:
\(g(x) = (22/x^2 + 5/x + 4/x^2) / (3 - 2/x^2 + r/x^2)\)
As x approaches infinity, the terms with the highest power of x dominate the fraction, so we can simplify the expression to:
\(g(x) \approx 22/3x^2\)
As x approaches negative infinity, the terms with the highest power of x are still dominant, so we get the same result:
\(g(x) \approx 22/3x^2\)
For similar questions on horizontal
https://brainly.com/question/30197734
#SPJ11
Sam needs to rent a van for a school field trip. Van Company A charges a one time fee of $250 plus $10 for each mile driven. Van Company B charges a one time fee of $150 plus $12 for each mile driven.
At how many miles are they the same price?
Answers
D.y = 10x + 250
y = 12x + 150 is the correct answer to the question





The inverse function of f(x)= 1/2x +10 shown.
h(x) =2x- ____
What’s the missing value
Answers
Answer:20
Step-by-step explanation:
y=1/2x+10
1/2x=y-10
x=2y-20
y=2x-20
A ____ should ALWAYS be representative of the general population.
A. Mode
B. Survey
C. Sample
D. Dot plot
(7th grade math)