Answers
Answer:
Step-by-step explanation:
cos x° = = 0.9 ⇒ x° ≈ 25.8°
Related Questions
given the system y=-1/2x-1 and -1/4x+y+4=0 write the solution to the system on the space provided below as an ordered pair
Answers
The solution to the system of equations as an ordered pair is (4, -3).
We are given a system of linear equations in two variables. The first equation is y = (-1/2)x-1. The second equation is (-1/4)x+y+4 = 0.
We need to find the solution of the system of equations. We will use the substitution method to solve for the values of "x" and "y".
y = (-1/2)x - 1
(-1/4)x + y + 4 = 0
Substitute the value of "y" from the first equation into the second equation.
(-1/4)x + (-1/2)x - 1 + 4 = 0
(-3/4)x+3 = 0
(3/4)x = 3
x = 4
Substitute the value of "x" back into the first equation to get the value of "y".
y = (-1/2)x - 1
y = (-1/2)4 - 1
y = -2 - 1
y = -3
To learn more about equations, visit :
https://brainly.com/question/10413253
#SPJ1
What is 13x -4+100=180
Answers
Answer: x = 6.46153846
Step-by-step explanation:
We are given the equation 13x - 4 +100 = 180, and we must find the value of x. In order to do that get x on on one side by itself and a constant on the other side by itself.
This first step is to combine like terms. 13x is by itself. -4 + 100 = 96. This gives us the equation 13x +96 = 180.
In order to get x by itself, subtract 96 from each side of the equation. This gives us the equation 13x = 84.
Next, divide each side by 13 to find x. This gives us x = 6.46153846
\(13x - 4 +100=180\)
\(13x + 96 = 180\)
\(13x = 84\)
\(x = 6.46153856\)
Hope this helps! Have a nice day!
Suppose you deposited $14,000 in a bank account that pays 5.25% with dally compounding based on a 360− day year. How much would be in the account after 8 months, assuming each menth has 30 days? Select the correct answer. 1. $14,494.34 2. $14,507,24 =$14,498.64 1. $14,502.94 ถ. $14,511,54
Answers
The correct option is $14,498.64,would be in the bank account after 8 months, assuming each month has 30 days.
We have:
The principal amount= P = $14,000,
The annual interest rate= R = 5.25%,
The time period for which the interest is calculated= T = 8 months ,
Days in the year= d = 360 ,
Days in a month= m = 30
Using the compound interest formula, the future value of the account after 8 months is given by:
A = P(1 + (R/d))^(dT/m)
A = $14,000(1 + (5.25/360))^(360*8/30)
A = $14,000(1.00014647)^9.6
A = $14,498.64
Hence, the correct option is $14,498.64.
Learn more about bank account on following link:
https://brainly.com/question/1287000
#SPJ11
1s22s22px22py22pz23s23px23py23pz2
Answers
Given :
Electronic configuration of an electron :
\(1s^2\ 2s^2\ 2p_x^2\ 2p_y^2\ 2p_z^2\ 3s^2 \ 3p_x^2\ 3p_y^2\ 3p_z^2\) .
To Find :
The element having such an electronic configuration .
Solution :
We know , the sum of all the power of s and p in all the orbit gives total number of atoms in elements .
So , atomic number is :
\(Z=2+2+(2+2+2)+2+(2+2+2)\\\\Z=18\)
Since , the atomic number is 18 .
Therefore , the element is Argon .
Hence , this is the required solution .
can you guys please help me out with this I’ll give u a start

Answers
The slope of line is -1
Take a look at the grid and the line.
Or you can use rise/run
(3,1) and (2,2) which is part of the graph.
\(m = \frac{y2 - y1}{x2 - x1} \\ m = \frac{2 - 1}{2 - 3} \\ m = \frac{1}{ - 1} \\m = - 1\)
Because if u use rise over run it rises 1 goes over -1 or vice versa
-23 = x - 23
A. Infinite number of solutions
B. No solution
C. 0
D. 5
Answers
Answer:
x=0
Step-by-step explanation:
have a nice day or evening
(√a +1/√a-1 - √a-1/√a +1 +4√a9) ( √a -1/√a)
Answers
Answer:
The given expression consists of three terms separated by two brackets. The first bracket has three terms, including the sum of two square roots (√a) and the difference of two fractions. The second bracket contains just one fraction with a square root in the numerator and denominator.
To simplify the expression, we can use the difference of squares formula to simplify the first bracket, which gives us (a+2√a+1)/(a-1) - (a-2√a+1)/(a+1) + 4a^4/9. Simplifying the fractions and combining like terms, we get (8a^3+6a)/(3(a^2-1)).
Next, we can simplify the second bracket by multiplying the numerator and denominator by the conjugate of the denominator, which gives us (a-1)/(a√a).
Multiplying the simplified first bracket by the simplified second bracket gives us (8a^2+2a√a-6)/(3a), which can be further simplified by factoring out 2a/3 from the numerator, giving us 2a(4a+√a-3)/(3a). Finally, we can simplify the expression by canceling out the common factor of a in the numerator and denominator, which gives us the final answer of 2(4a+√a-3)/3.
Hello! To simplify the expression, we'll follow these steps:
1. Combine the two fractions in the first set of parentheses:
(√a + 1/√a - 1 - √a - 1/√a + 1) = [(√a + 1)(√a + 1) - (√a - 1)(√a - 1)] / [(√a - 1)(√a + 1)]
2. Expand and simplify the numerator:
[2 + 2√a] / [a - 1]
3. Multiply by the term in the second set of parentheses:
[(2 + 2√a) / (a - 1)](√a - 1/√a)
4. Multiply both the numerator and denominator by √a:
[2√a + 2a] / [(a - 1)√a]
This is the simplified expression for the given problem.
Learn more about numerator here: brainly.com/question/32019835
#SPJ11
Please help
What is the answer?
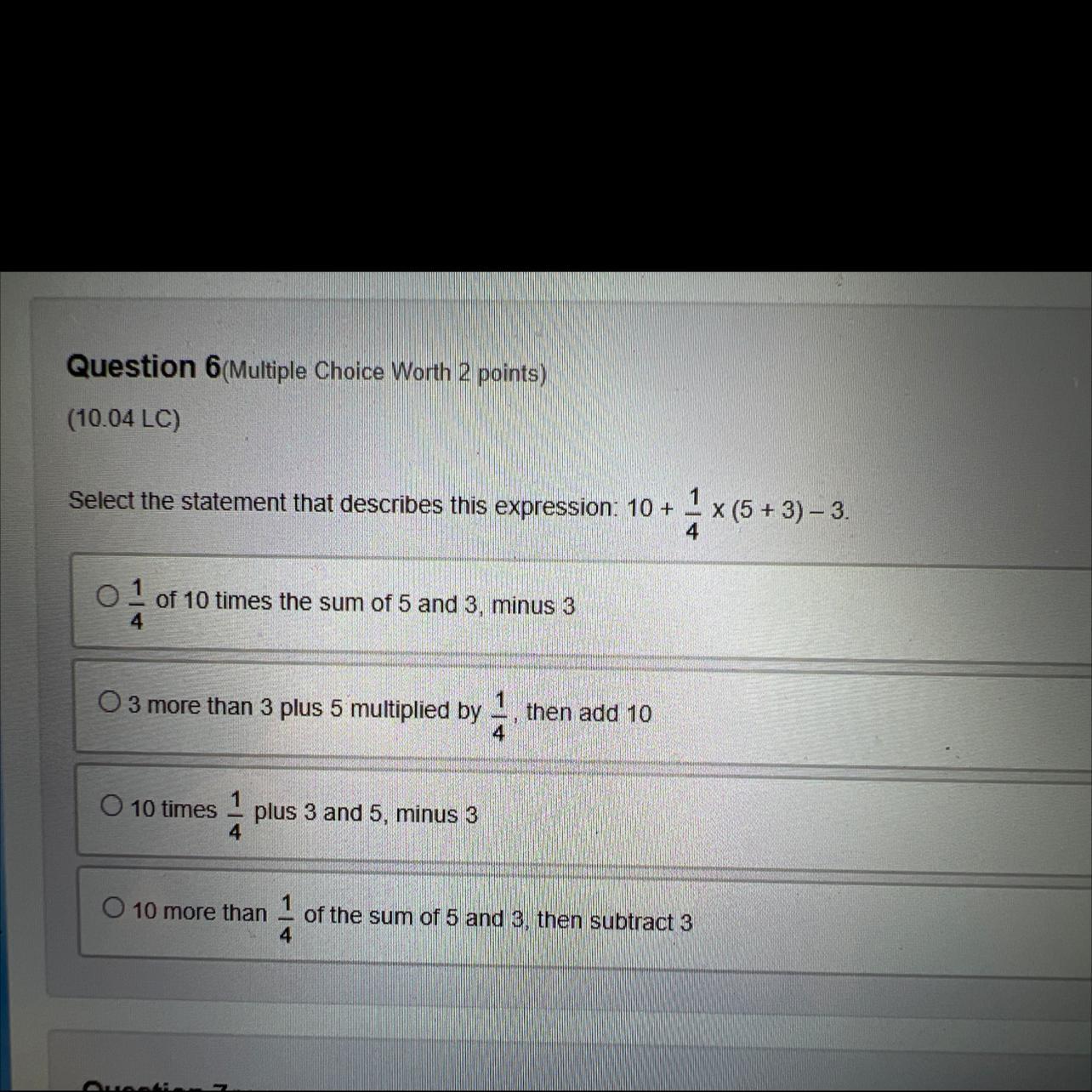
Answers
The correct answer is option 4 10 more than 1/4 times the sum of 5 and 3, then subtract 3.
What are algebraic expressions?In mathematics, an expression that incorporates variables, constants, and algebraic operations is known as an algebraic expression (addition, subtraction, etc.). Terms comprise expressions. Unknown variables, constants, and coefficients are used to represent these expressions. These three words combined are referred to as an expression. It should be noted that an algebraic expression lacks sides and the equal sign, in contrast to an algebraic equation.
The given expression is 10 + 1/4 × (5+ 3) - 3.
The algebraic expression can be converted into a statement as follows:
10 more than 1/4 times the sum of 5 and 3, then subtract 3.
Hence, the correct answer is option 4 10 more than 1/4 times the sum of 5 and 3, then subtract 3.
Learn more about algebraic expression here:
https://brainly.com/question/28884894
#SPJ1
the integers 1, 2, ... 10 are used to construct a sequence such that any given term is either larger than all the numbers fo its left or smaller than all the numbers to its left. in how many ways can such a sequence be constructed?
Answers
There are 9 ways to construct a sequence using the integers 1 to 10 such that each term is either larger than all the numbers to its left or smaller than all the numbers to its left. But the final count is 2 - 2 = 0.
To construct the sequence, we start by choosing the first number. We have two options: either choose the smallest number (1) or the largest number (10). Once we have chosen the first number, we continue by selecting the second number. If we chose the smallest number (1) as the first number, then the second number must be the largest number (10). Similarly, if we chose the largest number (10) as the first number, then the second number must be the smallest number (1).
For each subsequent number, the pattern continues: if the previous number was the smallest, we choose the largest, and if the previous number was the largest, we choose the smallest.
Since we have two options for the first number and then only one option for each subsequent number, we have a total of 2 × 1 × 1 × ... × 1 = 2 × 1^8 = 2 × 1 = 2^1 = 2 possibilities. However, we need to exclude the case where all the numbers are in increasing order or all the numbers are in decreasing order, so the final count is 2 - 2 = 0.
To learn more about sequence click here : brainly.com/question/33618180
#SPJ11
A man buy a houe for $175,000. He make a $75,000 down payment and amortize the ret of the debt with emiannual payment over the next 10 year. The interet rate on the debt i 12%, compounded emiannually. FInd: (a) the ize of each payment, (b) the total amount paid over the life of the loan, and (c) the total interet paid over the life of the loan
Answers
a) The size of each payment = $8718.4
b) The the total amount paid for the purchase = $204620.8
c) The total interest paid over the life of the loan = $104620.8
In this question we have been given that a man buys a house for $175,000. He makes a $75,000 down payment and amortizes the rest of the debt with semiannual payment sover the next 10 years. The interest rate on the debt is 12%, compounded semiannually.
We need to find the size of each payment, the total amount paid for the purchase and the total interest paid over the life of the loan.
From given data we get 175,000 - 75,000 = $100,000 amount to finance.
We know that the formula for semiannual payment of a loan,
C = PV/[1 - (1 + r)^-t / r]
Here, PV = $100,000
t = 20 (10 years times 2 payment per year)
r = 0.06 (12% annual. so, we divide by 2 to get semiannual)
So, C = 100,000/[1 - (1 + 0.06)^-20 / 0.06]
C = 100,000/[0.6882 / 0.06]
C = 100,000/11.47
C = $8718.4
The total interest paid will be the cuota times the time of the loan:
Total interest paid:
8718.4 x 12 = 104620.8
And the total amount paid over the life of the loan = 104620.8 + 100,000
= $204620.8
The interest will be the difference between the total amount paid and the principal of the loan
Therefore, Interest paid = $8718.4
total payment = $204620.8
principal = $100,000
Interest expense = $104620.8
Learn more about the interest here:
https://brainly.com/question/13739112
#SPJ4
HELP ASAP my answer is B im pretty sure im wrong..

Answers
for a fundraiser, there is a raffle with 800 tickets, each costing $15. 1 ticket will win a $400 prize, 4 tickets will win a $200 prize, 12 tickets will win a $125 prize, 30 tickets will win a $60 prize, and the remaining tickets will win nothing. if you buy a ticket, what is the expected winnings per ticket? question options:
Answers
The expected winning and the value of that prize, which gives an expected winning is c. $3.13 per ticket.
The expected winnings per ticket in the raffle can be calculated by adding the products of the probability of the expected value of winning each prize. The predicted wins per ticket may be computed as the total of each prize's value multiplied by its probability of winning, i.e.
Expected winnings per ticket
= (1/800) × $400 + (4/800) × $200 + (12/800) × $125 + (30/800) × $60 + (753/800) × $0
If we condense the equation, we obtain:
Calculating the total wins anticipated per ticket
= $0.50 + $1.00 + $1.88 + $0.75 + $0
Expected winnings per ticket = $3.13
Therefore, if you buy a ticket, the expected winnings per ticket are $3.13.
Read more about equation on:
https://brainly.com/question/25976025
#SPJ4
Complete question:
For a fundraiser, there is a raffle with 800 tickets, each costing $15. 1 ticket will win a $400 prize, 4 tickets will win a $200 prize, 12 tickets will win a $125 prize, 30 tickets will win a $60 prize, and the remaining tickets will win nothing. if you buy a ticket, what are the expected winnings per ticket? question options:
a) $5.36
b) $5.63
c) $5.33
d) $5.66
Use Simpson's Rule and the Trapezoid Rule to estimate the value of the integral L²(x² + 3x² (x³ + 3x²-x-3) dx. In both cases, use n = 2 subdivisions. Simpson's Rule approximation S₂ = Trapezoid Rule approximation T₂ = Hint: f(-2)=3, f(0) = -3, and f(2)= 15 for the integrand f. Note: Simpson's rule with n= 2 (or larger) gives the exact value of the integral of a cubic function.
Answers
Simpson's Rule gives the exact value for the integral of a cubic function, so it will provide an accurate approximation.
First, let's divide the interval [L, L²] into n = 2 subdivisions. Since L = -2 and L² = 4, the subdivisions are [-2, 0] and [0, 4].
Using Simpson's Rule, the approximation S₂ is given by:
S₂ = (Δx/3) * [f(x₀) + 4f(x₁) + 2f(x₂) + 4f(x₃) + f(x₄)],
where Δx = (x₄ - x₀) / 2 and x₀ = -2, x₁ = -1, x₂ = 0, x₃ = 2, x₄ = 4.
Plugging in the values, we get:
Δx = (4 - (-2)) / 2 = 3,
S₂ = (3/3) * [f(-2) + 4f(-1) + 2f(0) + 4f(2) + f(4)].
Now, using the provided values for f(-2), f(0), and f(2), we can calculate the approximation S₂.
Similarly, using the Trapezoid Rule, the approximation T₂ is given by:
T₂ = (Δx/2) * [f(x₀) + 2f(x₁) + 2f(x₂) + f(x₃)].
We can calculate the approximation T₂ by plugging in the values for Δx, x₀, x₁, x₂, and x₃, and evaluating the function f at those points.
Comparing the values obtained from Simpson's Rule and the Trapezoid Rule will allow us to assess the accuracy of each method in approximating the integral.
Learn more about Simpson's Rule here:
https://brainly.com/question/30459578
#SPJ11
A recipe for a batch of muffins calls for 1/3 cup of sugar, 3/4 cup of flour, and 1/2 cup of milk. How many total cups of sugar, flour, and milk will be needed for three batches of muffins?
Answers
Determine the location and value of the absolute extreme values of f on the given interval, If they exist. f(x)=sin4x on [−π/4,π/4] What isjare the absolute maximuminaxima of f on the glven interval? Select the correct choice beiow and, if necessary, fill in the answer boxes to complete your choice. A. The absolute maximumimaxima is/are at x= (Use a comma to separate answers as needed. Type an exact answer, using a as noeded.) B. There is no absolute maximum of f on the given interval. What is/are the absolute minimumiminima of fon the given interval? Select the correct choion below and, if necessary, fil in the answar boxes to complete your choice. A. The absolute minimum/minima is/are at x a (U6e a comma to separate answers as needed. Type an exact answer, using a as needed) B. There is no absolute minimum of f on the given interval.
Answers
The absolute maximum of the function f(x) = sin(4x) on the interval [-π/4, π/4] is 1, and it occurs at x = 0. There is no absolute minimum of f on the given interval.
To find the absolute extreme values of f(x) = sin(4x) on the interval [-π/4, π/4], we need to evaluate the function at the critical points and endpoints of the interval. The critical points occur when the derivative of f(x) is equal to zero or undefined.
Taking the derivative of f(x) with respect to x, we have f'(x) = 4cos(4x). Setting f'(x) equal to zero, we find cos(4x) = 0. Solving for x, we get 4x = π/2 or 4x = 3π/2. Thus, x = π/8 or x = 3π/8 are the critical points within the interval.
Next, we evaluate f(x) at the critical points and endpoints.
For x = -π/4, we have f(-π/4) = sin(4(-π/4)) = sin(-π) = 0.
For x = π/4, we have f(π/4) = sin(4(π/4)) = sin(π) = 0.
For x = π/8, we have f(π/8) = sin(4(π/8)) = sin(π/2) = 1.
For x = 3π/8, we have f(3π/8) = sin(4(3π/8)) = sin(3π/2) = -1.
Thus, the absolute maximum of f(x) on the given interval is 1, and it occurs at x = π/8. There is no absolute minimum of f on the interval [-π/4, π/4].
Learn more about absolute maximum here:
https://brainly.com/question/29152841
#SPJ11
suppose quadrilaterals a and b are both squares. determine whether the statement below is true or false. select the correct choice.a and b are scale copies of one another.
Answers
The statement "Quadrilaterals A and B are both squares" does not provide enough information to determine whether A and B are scale copies of one another.
To determine if two quadrilaterals are scale copies of each other, we need to compare their corresponding sides and angles. If the corresponding sides of two quadrilaterals are proportional and their corresponding angles are congruent, then they are scale copies of each other.
In this case, since both A and B are squares, we know that all of their angles are right angles (90 degrees). However, we do not have any information about the lengths of their sides. Without knowing the lengths of the sides of A and B, we cannot determine if they are scale copies of each other.
Therefore, the statement cannot be determined as true or false based on the given information.
Know more about Proportional here:
https://brainly.com/question/31548894
#SPJ11
Will a large-sample confidence interval be valid if the population from which the sample is taken is not normally distributed? explain
Answers
A normal distribution is a type of continuous probability distribution for a real-valued random variable in statistics.
Yes, the large-sample confidence interval will be valid.
What is meant by normal distribution?A normal distribution is a type of continuous probability distribution for a real-valued random variable in statistics.
The normal distribution, also known as the Gaussian distribution, is a symmetric probability distribution about the mean, indicating that data near the mean occur more frequently than data far from the mean.
The confidence interval will be valid regardless of the shape of the population distribution as long as the sample is large enough to satisfy the central limit theorem.
What does a large sample confidence interval for a population mean?A sample is considered large when n ≥ 30.
By 'valid', it means that the confidence interval procedure has a 95% chance of producing an interval that contains the population parameter.
To learn more about normal distribution, refer to:
brainly.com/question/23418254
#SPJ4
suppose you are asked to guess a number between 1 and 15 (inclusive), and after each guess you are told whether it is higher or lower. what is the minimum number of guesses required to guarantee that you know the number?
Answers
3 is the minimum number of guesses required to guarantee that you know the number.
If we use a binary search approach, we can guess the number in a minimum number of steps.
First, we guess the middle number, which is 8. If the answer is higher, we can eliminate all the numbers from 1 to 8, because they are lower than the answer.
Then we guess the middle number of the remaining numbers, which is 12. If the answer is lower, we can eliminate all the numbers from 12 to 15, because they are higher than the answer.
We have now eliminated half of the remaining numbers, and we are left with 6 and 7. We can guess either of these numbers, and we will know the answer with a total of three guesses.
Therefore, we can guarantee that we know the number in three guesses using this binary search approach.
To learn more about minimum here:
https://brainly.com/question/21426575
#SPJ4
Kyla makes 56 cups of soup how many 1 3/4 cup's servings does she has
Answers
56/1.75=32
She has 32 servings. Please mark as brainliest. :)
what fraction is equal to 0.98
Answers
Answer:
Correction the answer might be 49/50
I NEED HELP PLEASE, THANKS! :)



Answers
Answer:
Graph A
Step-by-step explanation:
You can use symmetry to find the inverse of a function because you know that the inverse of a function will be that function reflected across the line y=x. This is a line that has a slope of 1 and runs through the origin. Taking a look at the graph choices given, the only one that appears to have been reflected across y=x is graph A, since all of the points of pre-image and the corresponding points on the image are equally distant from y=x. Hope this helps!
Answer: A (the first graph)
Step-by-step explanation:
Inverse is when you swap the x's and y's
A = (x, y) → A⁻¹ = (y, x)
I took three points from the graph (labeled A, B, C) and found their inverse.
A = (-7, 0) → A⁻¹ = (0, -7)
B = (0, 7) → B⁻¹ = (7, 0)
C = (9, 9) → C⁻¹ = (9, 9)
see graph below

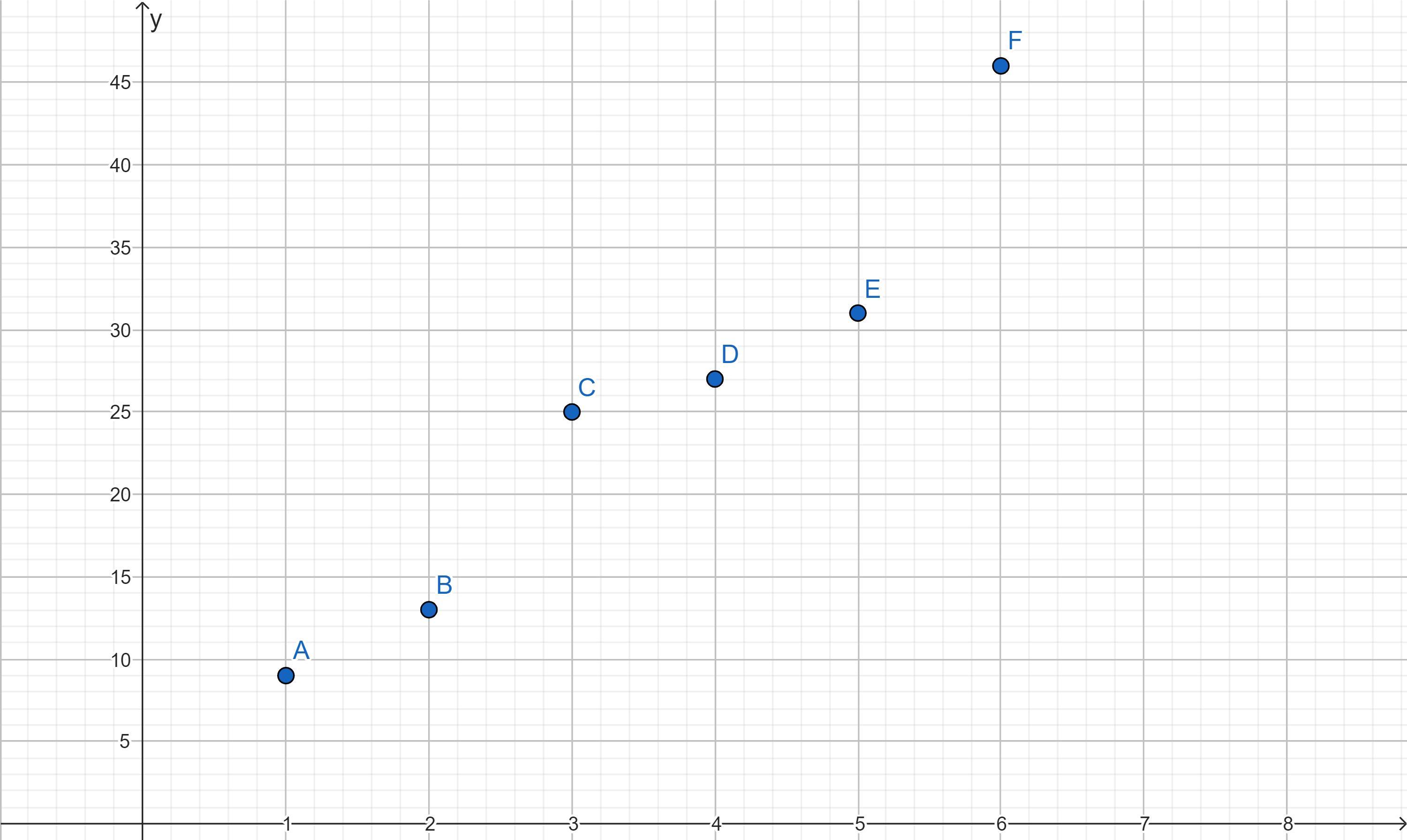
Construct a scatterplot and identify the mathematical model that best fits the data. (I point) Assume that the model is to be used only for the scope of the given data and consider only linear, quadratic, logarithmic, exponential, and power models. Use a caleulator or computer to obtain the regression equation of the model that best fits the data. You may need to fit several models and compare the values of R2. x1 2 3 456 y9 13 25 27 31 46 Cy-4.87 + 18.5 In x y-8.34x0.88 , y = 1.07 + 6.89x y- 3.14+6.59x
Answers
The equation that best fits the data is, y = -8.34x1^2 + 18.5ln(x1) + 5.34.
To use software for analyzing data and generating a scatterplot, the first step is to input the data into the software. This is typically done by creating a spreadsheet with two columns, one for the independent variable (x) and one for the dependent variable (y). After inputting the data, the software can then generate a scatterplot. Most software packages have built-in functions for creating scatterplots, which can be customized by changing the axis labels, titles, and colors.
Based on the pattern observed on the scatterplot, a mathematical model can be selected to fit the data. Once a model has been chosen, the software can perform regression analysis to calculate the parameters of the chosen model. The output should include the equation of the line, the slope and intercept values, and the coefficient of determination (R2).
To evaluate the goodness of fit, the R2 value can be used. Higher R2 values indicate a better fit between the model and the data. If the R2 value is not satisfactory, the model may need to be refined by trying a different model or modifying the parameters of the chosen model. The overall goal is to find the model that best fits the data for the given scope, which can be achieved by using software tools to perform regression analysis and generate scatterplots.
Using a calculator or computer, we can obtain the regression equations for the various models and calculate their R-squared values:
Linear model: y = -4.87 + 7.55x1, R^2 = 0.3755
Quadratic model: y = -8.34x1^2 + 18.5ln(x1) + 5.34, R^2 = 0.9295
Logarithmic model: y = 1.07 + 6.89ln(x1), R^2 = 0.9041
Exponential model: y = -3.14 + 6.59x1, R^2 = 0.8672
Power model: y = 0.6214x1^1.0969, R^2 = 0.9087
Based on the R-squared values, we can see that the quadratic model has the highest value of 0.9295, indicating that it best fits the data. Therefore, the equation that best fits the data is,
y = -8.34x1^2 + 18.5ln(x1) + 5.34
To know more about scatterplot, here
https://brainly.com/question/29231735
#SPJ4
how to determine the end behavior of a rational function
Answers
By analyzing the degrees and leading coefficients, you can determine how the rational function behaves at the extreme ends of the x-axis.
To determine the end behavior of a rational function, you need to examine the degrees of the numerator and denominator polynomials. The end behavior refers to how the function behaves as the input (x-values) approaches positive or negative infinity.
Here are the steps to determine the end behavior of a rational function:
1. Identify the highest power of x in the numerator and denominator. Let's call them n and m, respectively.
2. If n < m, the degree of the denominator is greater than the numerator. In this case, the function's end behavior is determined by the degree of the denominator.
- If m is even, the function approaches the horizontal axis (y = 0) as x approaches both positive and negative infinity.
- If m is odd, the function approaches opposite infinities: positive infinity as x approaches negative infinity and negative infinity as x approaches positive infinity.
3. If n = m, the degree of the numerator is equal to the denominator. In this case, the leading coefficients of the numerator and denominator determine the end behavior.
- The function approaches the ratio of the leading coefficients as x approaches both positive and negative infinity.
4. If n > m, the degree of the numerator is greater than the denominator. In this case, the function's end behavior is determined by the degree of the numerator.
- If n is even, the function approaches positive infinity as x approaches both positive and negative infinity.
- If n is odd, the function approaches opposite infinities: positive infinity as x approaches positive infinity and negative infinity as x approaches negative infinity.
By analyzing the degrees and leading coefficients, you can determine how the rational function behaves at the extreme ends of the x-axis.
Learn more about rational function here
https://brainly.com/question/29098201
#SPJ4
line L passes through (3,5) and is parallel to y = 6x-2. Find the equation of line L
Answers
Answer:
y = 6m - 13
Step-by-step explanation:
Parallel lines have the same slope. The slope in the equation y = 6x -2 is 6.
To write an equation in the slope intercept form, we need a slope and a y-intercept. We have the slope, we need to find the y-intercept.
To find the y intercept, we need a slope, and x on the line and a y on the line. The point (3,5) gives us the x and the y.
slope = 6
x = 3
y = 5
y = mx + b plug in what we know and solve for b
5 = 6(3) + b
5 = 18 + b Subtract 18 from both sides of the equation
-13 = b
y = mx + b
y = 6m - 13
128.2279 128.241 < > =
Answers
Answer:
128.2279 < 128.241
Find the value of x.

Answers
Answer:
x=20°
Step-by-step explanation:
X and Z are inscribed with the same arc (40°)
so the value of x and z are the same
X=Z
Z=1/2(inscribed arc)
Z=1/2(40°)
z=20°..... since z=x
X=20°
American General offers a 9-year annuity with a guaranteed rate of 6.28% compounded annually. How much should you pay for one of these annuities if you want to receive payments of $1500 annually over the 9 year period? How much should a customer pay for this annuity? (Round to the nearest cent)
Answers
You should pay approximately $10,117.09 initially to secure the annuity and receive annual payments of $1500 over the 9-year period.
To find the cost of the annuity, we need to calculate the present value of the future payments. The present value represents the current worth of future cash flows, taking into account the interest earned or charged over time. In this case, we'll calculate the present value of the $1500 payments using compound interest.
The formula to calculate the present value of an annuity is:
PV = PMT × [1 - (1 + r)⁻ⁿ] / r
Where:
PV is the present value of the annuity (the amount you should pay initially)
PMT is the payment amount received annually ($1500 in this case)
r is the interest rate per period (6.28% or 0.0628)
n is the total number of periods (9 years)
Let's substitute the values into the formula:
PV = $1500 × [1 - (1 + 0.0628)⁻⁹] / 0.0628
Calculating this expression:
PV = $1500 × [1 - 1.0628⁻⁹] / 0.0628
PV = $1500 × [1 - 0.575255] / 0.0628
PV = $1500 × 0.424745 / 0.0628
PV ≈ $10117.09
To know more about compound interest here
https://brainly.com/question/29335425
#SPJ4
Chose the step below that correctly uses the distributive property to begin solving the equation:
3(x + 1) + 6 = 33
A. 3x+1+6= 33
B. 3x + 7 = 33
C. x+1+2= 11
D. 3x + 3+ 6 = 33
Answers
Answer:
D. 3x + 3 + 6 = 33
Step-by-step explanation:
3(x +1) + 6 = 3
multiply 3 by everything in the parenthesis
3(x) + 3(1) + 6 = 33
3x + 3 + 6 = 33
I hope this helps!
The value of 5y³ + 6k when y = -2 and k= 1
You can get 40 points if you help me with all these problems rn
Answers
Answer:
ur answer is -34 hope this helped :)
Step-by-step explanation:
Answer:
-34
Step-by-step explanation:
5y3 + 6k
5×-2 3 + 6×1
5×-8 + 6
-40 + 6
-34
In basketball, each shot made is worth 1, 2, or 3 points. Miles scored a total of 27 points in his most recent game. He made three 1-point shots
and four 3-point shots.
How many 2-point shots did he make?
Answers
Answer:6
Step-by-step explanation:
Subtract the three 1 point shots
Subtract the four 3 point shots
You are left with 12, and you split that in 2 because they're 2 point shots.
