Answers
Answer:
B, or in other words, the last solution is correct.
Step-by-step explanation:
Parallel lines haves the same slope, meaning that Street 2 will have the same slope as Street 1. Street one, according to the graph, has a slope of 1. Thus, Street 2 will have a slope of 1.
By this logic, we can get rid of A and C as choices, as they have a slope of -2 or 2. Now we have choices B and D left.
It can't be B, as the slope is -1, not 1.
Therefore, the answer is D.
Related Questions
what is 10×27.54????????
Answers
Remember that when you multiply a number by 10, the decimal point is moved one place to the right. Then:
\(10\times27.54=275.4\)Therefore, the answer is 275.4
can someone help me on this question please
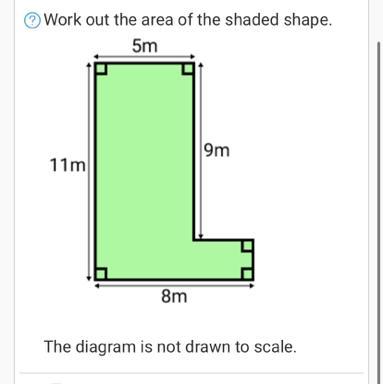
Answers
Answer:
61m^2
Step-by-step explanation:
1. Split the shape into squares or rectangles
5x9 Rectangle, 8x2 Rectangle
2. Find Area of Each Individual Shape
45, 16
3. Add Areas Together
45+16=61
4. Add Units Squared to the final answer
61m^2

A circular mosaic has radius 3 meters. Find the area. Round your answer to the nearest hundredth.
Group of answer choices
56.52 square meters
18.84 square meters
28.26 square meters
6.14 square meters
Answers
A circle is a round-shaped figure that has no corners or edges. If a circular mosaic has radius 3 meters then the area is 28.26 square meters.
What is Circle?A circle is a round-shaped figure that has no corners or edges. In geometry, a circle can be defined as a closed, two-dimensional curved shape.
Given that a circular mosaic has radius 3 meters.
We need to find the area of circular mosaic.
Area of circle=πr²
Here r=3
π=3.142
Substitute the values of pi and r in Area formula
Area =3.142*3²
=3.142*9
=28.26
Therefore area of circular mosaic is 28.26 square meters.
To learn more on Circle click:
https://brainly.com/question/11833983
#SPJ1
Susan is attending a talk at her son's school. There are 8 rows of 10chairs where 54 parents are sitting. Susan notices that every parent is either sitting on their own or next to just one other person. What is the largest possible number of adjacent empty chairs in a single row at that talk?
Answers
Answer:
The largest possible number of adjacent empty chairs in a single row is 3
Step-by-step explanation:
The parameters given are;
The number of chairs = 8 × 10 = 80 chairs
The number of parents = 54
Sitting arrangements of parents = Alone or to one other person
Therefore;
The maximum number of parents on a row = 1 + 1 + 0 + 1 + 1 + 0 + 1 + 1 + 0 + 1 = 7
Hence when the rows have the maximum number of parents occupying the seats we have for the 8 rows;
7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56
But there are only 54 parents, therefore, up to the 7th row will have 7 parents while the 8th row will have only 5 parents to make the possible sitting arrangement to be as follows;
7 + 7 + 7 + 7 + 7 + 7 + 7 + 5 = 54
The sitting arrangement for the 8th row is therefore
1 + 1 + 0 + 1 + 1 + 0 + 1 + 0 + 0 + 0
Hence there will be three empty seats in the 8th row making the largest possible number of adjacent empty chairs in a single row = 3.
The value of y varies directly with x. If x=104, then y=78. What is the value of x when y=39?
58
58
52
52
29.25
29.25
69.3
Answers
Answer: 52
Step-by-step explanation:
Since the value of y varies directly with x, y = kx where k is a constant.
Since x=104, then y=78, we need to calculate the constant k. This will be:
y = kx
78 = 104k
k = 78/104
k = 0.75
What is the value of x when y=39?
Since y = =kx
39 = 0.75x
x = 39/0.75
x = 52
hey please help i’ll give brain

Answers
Answer:
The answer is 6. commutative property of multiplication states that no matter the order, as long as all numbers are there, it equals the same amount.
Step-by-step explanation:
Answer:
6
Step-by-step explanation:
It's more like the missing property. This question is an example of the commutative property for multiplication. It does not matter what order you do the multiplying. 4*6 is the same as 6 * 4
How do you do substitution on the two equations explain pls

Answers
Answer:
You simply separate like terms
if length of a rectangle is (x+7) and breath is (x+5). find the area of the rectangle
Answers
Step-by-step explanation:
Area of rectangle is length x breadth.
Area = (x + 7)(x + 5)
= (x² + 5x + 7x + 35)
= (x² + 12x + 35)
HELP PLZ 30 POINTS UwU

Answers
Angle 1 = 130°
Angle 2 = 124°
Angle 3 = 56°
Angle 4 = 52°
Angle 5 = 72°
Angle 6 = 94°
I primarily used the triangles to get my answers. Remember the angles in a triangle add up to 180°.
Answer:
Angle 1 = 130°
Angle 2 = 124°
Angle 3 = 56°
Angle 4 = 52°
Angle 5 = 72°
Angle 6 = 94°
Step-by-step explanation:
a six foot man standing 200 feet from a tower observes the angle of elevation to the top of the tower to be 67 degrees. how high is the tower?
Answers
So, the height of the tower is approximately 363.6 feet.
You can use trigonometry to solve this problem.
If we call the height of the tower "h" and the distance between the man and the base of the tower "d", then the angle of elevation is defined as the angle between the line of sight from the observer to the top of the tower and the horizontal line.
We can use the tangent function to relate the angle of elevation to the height and distance.
tan(67) = h/d
We know that the distance between the man and the tower is 200 feet. We can use this information to find the height of the tower.
h = d * tan(67)
h = 200 * tan(67)
The height of the tower is approximately 363.6 feet.
Please note that due to the approximation of the trigonometric functions, the answer may not be exactly as calculated.
To learn more about angle of elevation
Visit; brainly.com/question/16716174
#SPJ4
Given box with
h= 2x-2 l = x + 5 w= 3x + 4 Write a polynomial that represents the volume of the box. Please use the palette below to enter your answer.
Answers
Here volume of the cuboid is 6x³ + 32x² + 2x - 40.
A cuboid's volume is calculated by summing its length, width, and height.
The number that is used to calculate how much room there is inside a cuboid is called its volume. A cuboid is a common three-dimensional form that surrounds us. Based on a form's parameters, such as its length, width, and height, the term "volume" is used to describe how much of that shape may be contained.
So Here,
height (h) = 2x - 2
Length (l) = 3x + 4
Breadth (b) = x + 5
Volume = l × b × h
= (3x + 4) × (x + 5) × (2x - 2)
= [(3x + 4)(x + 5)](2x - 2)
= (3x² + 13x + 20] (2x - 2)
Volume = 6x³ - 6x² + 38x² - 38x + 40x - 40
Volume (V) = 6x³ + 32x² + 2x - 40
To learn more about cuboid's volume
https://brainly.com/question/29424737
#SPJ4

130 is 1/10 of 13 true or false
Answers
Answer:
This is true.
Step-by-step explanation:
Finding 1/10 of a number is the same as dividing it by 10. 130 divided by 10 is 13.
Solve the following inequalities, if it is known that the function g is decreasing on its domain. g(5-x^2)≤g(3x-5), Dg=(-∞,4)
Answers
For the following inequalities, if it is known that the function g is decreasing on its domain. g(5-x^2)≤g(3x-5) the solution is mathematically given as
1 ≤ x < 6
What is the following inequalities g(5-x^2)≤g(3x-5)?
Generally, the equation for the inequalities is mathematically given as
g(5-x^2)≤g(3x-5)
therefore,
x^2<5x+6
-1< x <6
In conclusion, the solution to the inequalities are
1 ≤ x < 6
Read more about Inequality
https://brainly.com/question/19491153
Ared candle is 8 inches tall and burns at a rate of inch per hour. 1 A blue candle is 6 inches tall and burns at a rate of inch per hour. 5 After how many hours will both candles be the same height? Enter your answer in the box.
Answers
Answer:
After 8 hrs both candles would've burned out completely, so they'll, more or less, be at the same height.
PLEASEE HELP ASAP!! 50 POINTS!
Select the correct answer. The graph of function f is shown. If g(x) = -2f(x), which graph is the graph of function g?




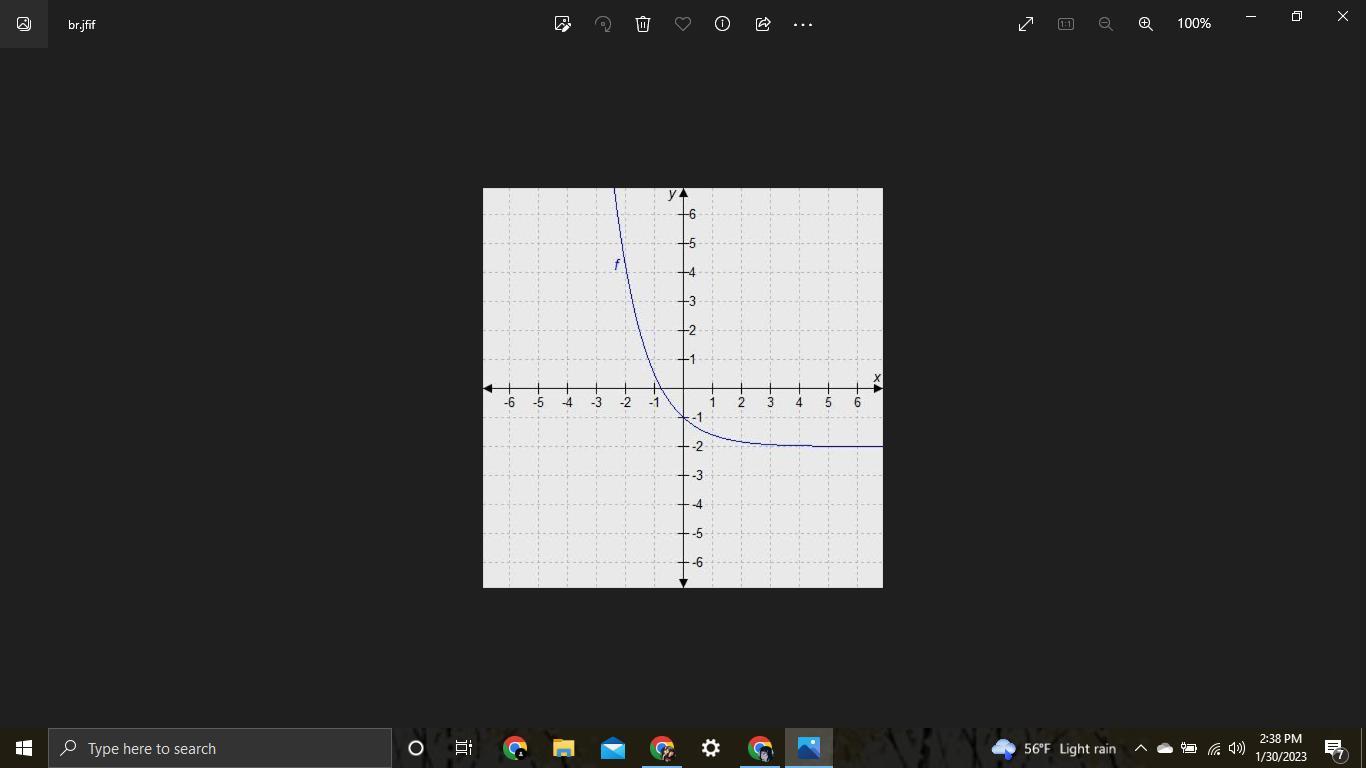
Answers
The graph of function f is shown. If g(x) = -2f(x), which graph is the graph of function g is show on the attachment
What is a graph?Note that the new function, g(x), provides a value for y that is -2 times the value returned by f(x). That means that for the same value of x, the resulting value of g(x) will be -2 times that provided by f(x).
See the attached image. The table shows how the values of y change for each value of x used in the respective function. Plot those new values to produce the graph.
Learn more about graphs on https://brainly.com/question/17267403
#SPJ1

Can someone help on this question from khanademy geometry. Finding the equation for the circle

Answers
The equation of the circle graphed in this problem is:
(x - 5)² + y² = 16.
What is the equation of a circle?The equation of a circle of center \((x_0, y_0)\) and radius r is given by:
\((x - x_0)^2 + (y - y_0)^2 = r^2\)
For the circle graphed, we have that:
The center is at point (5,0), hence \(x_0 = 5, y_0 = 0\).The radius is of 4 units.Hence the equation of the circle graphed is:
(x - 5)² + y² = 16.
More can be learned about the equation of a circle at https://brainly.com/question/24307696
#SPJ1
What is the answer for -3p(p+2) - (2p+3) using the distribution method?
Answers
Answer: -3p^2-8p-3
Step-by-step explanation: By distributing we get, -3p^2-6p-2p-3. Then simplify accordingly.
To figure out this problem, we need to break down the steps:
-3p(p + 2) - (2p + 3)
because -3p is next to the equation in parentheses, (p + 2), you should multiply -3p into both p and 2
-3p x p = -3p² (if you multiply a variable (p) by another of the same variable with no power, it becomes squared)
-3p x 2 = -6p
so the first part of the equation went from -3p(p + 2) to -3p² -6p
and the second part of the equation has no multiplying to do
so now we add like terms!
-3p² -6p - 2p + 3
-3p² -8p + 3
order from greatest power to least power (first goes the number/variable with the highest power, then the term with a variable, and lastly the number. Right now it is currently in the correct order).
-3p² -8p + 3 is your final answer
A partly-full paint can ha5 0.816 U.S. gallons of paint left in it. (a) What is the volume of the paint, in cubic meters? (b) If all the remaining paint is used to coat a wall evenly (wall area =13.2 m
2
), how thick is the layer of wet paint? Give your answer in meters. (a) Number Units (b) Number Units
Answers
(a) The volume of the paint in the can is approximately 0.003086 cubic meters.
(b) The thickness of the layer of wet paint on the wall is approximately 0.06182 meters.
:(a) To convert the volume of the paint from gallons to cubic meters, we need to use the conversion factor 1 U.S. gallon = 0.00378541 cubic meters. Given that the paint can has 0.816 U.S. gallons of paint left, we can calculate the volume in cubic meters by multiplying 0.816 by the conversion factor. The result is approximately 0.003086 cubic meters.
(b) To find the thickness of the layer of wet paint on the wall, we need to divide the volume of the paint (in cubic meters) by the area of the wall (in square meters). The remaining paint can cover an area of 13.2 square meters, so dividing the volume of the paint (0.003086 cubic meters) by the wall area (13.2 square meters) gives us approximately 0.0002333 meters or 0.06182 meters when rounded.
Learn more about volume here:
brainly.com/question/28058531
#SPJ11
9. Determine where the graph represents a function explain your answer.

Answers
The vertical line test is a visual test to determine if a graph represents a function; since a function can only have one output for every input if a vertical line intersects a curve in more that one point the it is not the graph of a function.
In this case we any vertical line will only intersect one point then we conclude that:
The graph represents a function. Using the vertical line test, the graph intersects any vertical line at only one point.
spent $95 buying 13 books to donate to the local elementary school. Activity books cost $5 each and story books cost $11 each, how many of each type of book did purchase?
Answers
Answer:
Number of Activity books = 8
Number of Storybooks = 5
Explanation:
Let x represent the number of activity books.
Let y represent the number of storybooks.
Let's go ahead and set up our equations as follows;
\(\begin{gathered} x+y=13\ldots\ldots\text{.}\mathrm{}\text{Equation 1} \\ 5x+11y=95\ldots\ldots\ldots\ldots\text{.Equation 2} \end{gathered}\)From equation 1, we can see that x = 13 - y
Let's go ahead and substitute the value of x into equation 2 and solve for y;
\(\begin{gathered} 5(13-y)+11y=95 \\ 65-5y+11y=95 \\ 6y=30 \\ y=\frac{30}{6} \\ y=5 \end{gathered}\)Since y = 5, let's substitute the value of y into equation 1 and solve for x;
\(\begin{gathered} x+5=13 \\ x=13-5 \\ x=8 \end{gathered}\)x+4 ≥ 9 and 2x-5 ≥3
x ≥ ?
Answers
Answer:
1. x ≥ 5
2. x ≥ 4
Step-by-step explanation:
1. 5 + 4 ≥ 9
2. 2(4)-5≥3
2x4= 8
8-5≥3
Which is the correct solution to ‐3x<21?

Answers
this is because, when dividing an inequality by a negative number, you must flip the inequality sign
-3x < 21
x > -7
Answer:
Top right
Step-by-step explanation:
When mult/dividing by a negative number, the sign always flips.
Consider the following vector function. r(t) = 3t, 1 2 t2, t2 (a) find the unit tangent and unit normal vectors t(t) and n(t).
Answers
The unit tangent vector t(t) is (3, 4t, 2t) / sqrt(9 + 20t^2), and the unit normal vector n(t) is (3, 4, 2t) / sqrt(25 + 4t^2).
The unit tangent vector t(t) of the given vector function r(t) = (3t, 1 + 2t^2, t^2) is obtained by dividing the derivative of r(t) by its magnitude. The derivative of r(t) is (3, 4t, 2t), and the magnitude of this vector is sqrt(9 + 20t^2). Therefore, t(t) = (3, 4t, 2t) / sqrt(9 + 20t^2).
The unit normal vector n(t) can be obtained by dividing the derivative of t(t) by its magnitude. The derivative of t(t) is (3, 4, 2t), and the magnitude of this vector is sqrt(25 + 4t^2). Thus, n(t) = (3, 4, 2t) / sqrt(25 + 4t^2).
These unit vectors t(t) and n(t) represent the direction of motion and the direction of the curve's curvature at each point t, respectively, providing valuable information about the behavior of the vector function r(t).
To know more about vector,
https://brainly.com/question/33923402#
#SPJ11
a polyhedron has all faces triangles or quadrilaterals, and $1001$ edges. what is the difference between the maximum and minimum possible numbers of faces?
Answers
Using Euler'formula, the difference between maximum and minimum possible numbers of faces is 96.
A polyhedron is a 3D shape with flat faces, straight edges, and sharp vertices (corners). "polyhedron" meaning "many" and "polyhedron" meaning "area". Therefore, when many planes are joined, they form a polyhedron.
Because all faces are triangles. So on a triangular base with triangular faces on both sides that meet at the vertex.
Therefore, the minimum number of triangular faces of a regular polyhedron is = 4
Next, the double pyramid has "2n" triangular faces. where n is a natural number greater than 2 and 'n' represents the number of sides of the base of the pyramid.
A polyhedron having equal quadrilateral faces is known as regular hexahedron.
quadrilateral faced polyhedron with total sides 100 and vertices 6 , then using Euler's formula
F + V-E = 2
=> F + 6- 100= 2 => F = 96 maximum faces possible = 96
Now the difference between maximum and minimum number of faces = 100 - 4 = 96
So the difference between maximum and minimum faces is 96.
To learn more about Polyhedron, refer:
https://brainly.com/question/27231951
#SPJ4
4PLEASE HELP ME THIS IS URGENT I WILL GIVE BRAINLIEST

Answers
Answer:
9.3 ft
Step-by-step explanation:
Simplify the expression.
6(z + 4) + 1 =
Answers
Answer:
6z+25
Step-by-step explanation:
6(z+4)+1
=6z+24+1
=6z+25
Answer: 4+2
Step-by-step explanation:
z=1
6(4+1=5)+1=6
11. Simplify the expression.
2x - 5(3x-4)
Answers
Answer:
Your answer is -13x + 20
Step-by-step explanation:
2x - 5*(3x - 4)
Discribute the -5.
2x + [ (-5)(3x) + (-5)(-4) ]
2x + [ (-15x +20) ]
2x - 15x + 20
- 13x + 20
What’s the value of x

Answers
Answer:
C. x=42
Step-by-step explanation:
16 + 3x + y = 180
126 + 16 + y = 180
y = 38
16 + 3x + 38 = 180
54 + 3x = 180
3x = 126
x=42
If you have 10 tennis players in a tournament with a round-robin setup, what is the total number of games they will need to play before each player has played every other player?
45, 15, 50, 8, 10, Any
Answers
In a 10-player round-robin tennis tournament, each player must play 45 games, and a total of 90 games will be played in the tournament.
A round-robin tournament is a type of competition in which every participant plays against every other participant. In a 10-player tournament, the number of games needed can be calculated using the formula for combination.
The density of a tournament can be defined as the number of games each player must participate in to play against every other player.
To calculate the density of a 10-player round-robin tournament, we use the formula
=> n(n-1)/2,
where n is the number of players.
In this case, n = 10. So, the density of the tournament is
=> 10(10-1)/2 = 45.
This means that each player must play 45 games in total, and each game involves 2 players.
So, there will be a total of
=> 45*2 = 90
games played in the tournament.
To summarize, The density of the tournament, 45 games per player, is calculated using the formula n(n-1)/2.
To know more about total here.
https://brainly.com/question/14286201
#SPJ4
Please help ASAP!!!!!!

Answers
Answer:
see explanation
Step-by-step explanation:
(f + g)(x) = f(x) + g(x), so
f(x) + g(x)
= x² + 5x + 6 + x + 3 ← collect like terms
= x² + 6x + 9
-------------------------------------------------
(f - g)(x) = (f(x) - g(x), so
f(x) - g(x)
= x² + 5x + 6 - (x + 3) ← distribute by - 1
= x² + 5x + 6 - x - 3 ← collect like terms
= x² + 4x + 3
---------------------------------------------------
(f • g)(x)
= f(x) × g(x)
= (x² + 5x + 6)(x + 3)
Each term in the second factor is multiplied by each term in the first factor, that is
x²(x + 3) + 5x(x + 3) + 6(x + 3) ← distribute parenthesis
= x³ + 3x² + 5x² + 15x + 6x + 18 ← collect like terms
= x³ + 8x² + 21x + 18
---------------------------------------------------------------
(\(\frac{f}{g}\) )(x)
= \(\frac{f(x)}{g(x)}\)
= \(\frac{x^2+5x+6}{x+3}\) ← factor the numerator
= \(\frac{(x+2)(x+3)}{x+3}\) ← cancel common factor (x + 3) on numerator/ denominator
= x + 2
