How do I solve a Pythagorean triangle of 7 squared + 2 squared and then the number after what would it be when u square root it
Answers
To solve a Pythagorean triangle of 7 squared + 2 squared, you need to use the Pythagorean theorem.
The Pythagorean theorem states that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides. In this case, the hypotenuse is the unknown side, which we'll call x. So, we have:
7² + 2² = x²
Simplifying this equation, we get:
49 + 4 = x²
53 = x²
To find the value of x, we need to take the square root of both sides:
√53 = x
So the answer to the problem is √53. When you square root it, you get a decimal approximation of approximately 7.28.
In summary, to solve a Pythagorean triangle, you need to use the Pythagorean theorem and find the square root of the sum of the squares of the other two sides to find the length of the unknown side.
Learn more about Pythagorean theorem here: https://brainly.com/question/28981380
#SPJ11
Related Questions
What is the perimeter of rhombus wxyz? startroot 13 endroot units 12 units startroot 13 endroot units 20 units
Answers
The correct option C.4 square root 13 units; is the obtained perimeter of the rhombus WXYZ.
Define the term rhombus?It is a unique instance of a parallelogram in which the diagonals meet at a 90-degree angle and all sides are equal. This is a rhombus' fundamental characteristic. A rhombus has a diamond-shaped shape.The congruence of the sides is one of the characteristics of rhombuses.
As a result, we only need to use the distance formula to get the length with one side.
Using the distance formula, find one side as;
d = √(x₂ - x₁)² + (y₂ - y₁)²
The distance at line YZ is:
YZ = √(5 - 3)² + (5 - 2)²
YZ = √13
Perimeter = 4 x (length of one side)
Perimeter = 4 √13
Thus, the obtained perimeter of the rhombus WXYZ is 4√13 units.
To know more about the rhombus, here
https://brainly.com/question/88523
#SPJ4
The correct question is-
What is the perimeter of rhombus wxyz?
A.square root 13 units
B.12 units
C.4 square root 13 units
D.20 units

the square root of 97 is between _ and _,and it is closer to_
Answers
Answer:
between 9 and 10. it is closer to 10
Someone help what would my average be if I got 100% on my both of my tests? I just wanna know
Answers
Answer:
To figure out your average, you add them together then divide by2
Step-by-step explanation:
I'm doing a test now please help!!!!!!
Ann and Tori wanted to estimate the average weight of an Oreo cookie to determine if it was less than advertised (34 grams for 3 cookies). They selected a random sample of 36 cookies and found the weight of each cookie (in grams). The mean weight was 11.3921 grams with a standard deviation of Sx= 0.0817 grams.
Construct and interpret a 90% confidence interval for the true mean weight of an Oreo cookie. Show your calculations and round your interval to 3 decimal places.
Answers
Answer:
the answer is equal to 90%of 11.3921 which is 1.25313= 1.253
A=2br÷6r
Make r the subject
Answers
Answer:
b / 3
Step-by-step explanation:
2br = 2r * b
6r = 2r * 3
A = 2br ÷ 6r
= ( 2r * b ) / ( 2r * 3 )
A = b / 3
What number is increased by 40% become 28?
a.5 b. 10 c. 15 d. 20
Answers
Answer:
d. 20
Step-by-step explanation:
28 ÷ (100%+40%)
= 28 ÷ 140%
= 28 ÷ 1.4 = 20
Answer:
option d
Step-by-step explanation:
Let the number be x
40% of x = 0.40x
Increased by 40% = 28
That is ,
x + 0.40x = 28
1.40x = 28
\(x = \frac{28}{1.40}\\\)
\(x = \frac{28 \times 100}{1.40 \times 100 } = \frac{28 \times 100}{140} =\frac{4 \times 100}{20} = 4 \times 5 = 20\)
Therefore, the number is 20
A bank officer wants to determine the amount of the average total monthly deposits per customer at the bank. He believes an estimate of this average amount using a confidence interval is sufficient. How large a sample should he take to be within $200 (MOE) of the actual average with 99% confidence? He assumes the standard deviation of total monthly deposits for all customers is about $1000
Answers
After calculating and analyzing the given question, the bank officer should be inclined to take a sample of at least 133 under the condition of within $200 (MOE) of the actual average with 99% confidence.
In the event of determining the size sample needed for understanding average total monthly deposits by implementing the formula
n = (z x Σ / E)²
here,
n = sample size,
z = z-score involving the desired level of confidence,
Σ = population standard deviation,
E = margin of error
Staging the values in the formula
n = (2.576 * 1000 / 200)² = 132.71
≈ 133
After calculating and analyzing the given question, the bank officer should be inclined to take a sample of at least 133 under the condition of within $200 (MOE) of the actual average with 99% confidence.
To learn more about monthly deposits,
https://brainly.com/question/31112326
#SPJ4
If 0° < θ < 90° or 180° < θ < 270°, explain why sin 2θ is always positive.
Answers
Using a trigonometric identity, since in the first quadrant and in the third quadrant the sine and the cosine have the same sign, \(\sin{2\theta}\) is always positive.
What is the trigonometric identity for sin 2θ?It is given by:
\(\sin{2\theta} = 2\sin{\theta}\cos{\theta}\)
In the first quadrant(0° < θ < 90°) and in the third(180° < θ < 270°), the sine and the cosine have the same sign, hence the multiplication is positive and \(\sin{2\theta}\) is always positive.
More can be learned about trigonometric identities at https://brainly.com/question/24496175
#SPJ1
Quadratic worded question
The owner of a fish shop bought x kilograms of salmon for $400 from the wholesale market. At the end of the day, all except for 2 kg of the fish were sold at a price per kg that was $10 more than what the owner paid at the market. From the sale of the fish, a total of $540 was made. Calculate how many kilograms of salmon the fish-shop owner bought at the market.
Answers
Answer: 23 kg
Step-by-step explanation:
Let's begin by using algebra to solve the problem.
Let x be the number of kilograms of salmon the fish-shop owner bought at the market.
We know that the total cost of the salmon was $400, so we can write:
400 = x * c
where c is the cost per kilogram of salmon.
We also know that all except for 2 kg of the fish were sold at a price per kg that was $10 more than what the owner paid at the market. So the price per kilogram of salmon at the fish shop was c + 10.
The total revenue from the sale of the fish was $540, so we can write:
540 = (x - 2) * (c + 10)
Now we can use these two equations to solve for x.
First, we can use the first equation to solve for c:
c = 400 / x
Then we can substitute this expression for c into the second equation:
540 = (x - 2) * (400/x + 10)
Simplifying this equation:
540 = 4000/x + 10x - 20 - 80/x
Multiplying both sides by x:
540x = 4000 + 10x^2 - 20x - 80
10x^2 - 20x - 4600 = 0
Dividing both sides by 10:
x^2 - 2x - 460 = 0
We can solve for x using the quadratic formula:
x = [2 ± sqrt(4 + 4*460)] / 2
x = [2 ± 44] / 2
Discarding the negative solution, we get:
x = (2 + 44) / 2
x = 23
Therefore, the fish-shop owner bought 23 kilograms of salmon at the market.
A _________ indicates the outer edge of a roadway, and it may be crossed only by traffic moving to or from the shoulder.
Answers
Answer:
edge lines
Step-by-step explanation:
What is the method of comparing Coefficient
Answers
Answer: In mathematics, the method of equating the coefficients is a way of solving a functional equation of two expressions such as polynomials for a number of unknown parameters. It relies on the fact that two expressions are identical precisely when corresponding coefficients are equal for each different type of term.
.
Need Help ASAP
Slope = -7;(4,-30)
Answers

Answer:
y=-7x-2
Step-by-step explanation:
I assume you need the equation for the line, so that's what I'm solving for here.
1. Start by putting the slope and the coordinates into point slope form, which is y-y1=m(x-x1)
y+30=-7(x-4)
2. Distribute -7 to (x-4) (or multiply x and -4 by -7).
y+30=-7x+28
3. Subtract 30 from both sides to get y by itself.
y=-7x-2
The camera cost $540 if the sales tax is 7.2% what is the tax charge and the total cost?
Answers
Solution:
The cost of the Camera is $540
The sales tax is 7.2%
To find the tax charge, the formula is
\(Tax\text{ charge}=Cost\text{ of item}\times\frac{sales\text{ tax }\%}{100}\)Substitute into the formula above
\(\begin{gathered} Tax\text{ charge}=540\times\frac{7.2}{100} \\ Tax\text{ charge}=\text{\$38.88} \end{gathered}\)Hence, the tax charged is $38.88.
The total cost of the Camera will be
\(=540+38.88=\text{\$578.88}\)Hence, the total cost of the Camera is $578.88
(a) Show that the vectors u1 = (2, 0, 3), u2 = (−3, 0, 2) and u3 = (0, 7, 0) form an orthogonal basis for R 3 .(b) Write v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (−3, 0, 2) and u3 = (0, 7, 0).
Answers
Main Answer:The linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
Supporting Question and Answer:
How can we express a vector as a linear combination of vectors using a system of equations?
To express a vector as a linear combination of vectors using a system of equations, we need to find the coefficients that multiply each given vector to obtain the desired vector. This can be done by setting up a system of equations, where each equation corresponds to the components of the vectors involved.
Body of the Solution:
(a) To show that the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3, we need to demonstrate two conditions: orthogonality and linear independence.
Orthogonality: We need to show that each pair of vectors is orthogonal, meaning their dot product is zero.u1 · u2 = (2)(-3) + (0)(0) + (3)(2) = -6 + 0 + 6 = 0
u1 · u3 = (2)(0) + (0)(7) + (3)(0) = 0 + 0 + 0 = 0
u2 · u3 = (-3)(0) + (0)(7) + (2)(0) = 0 + 0 + 0 = 0
Since the dot product of every pair of vectors is zero, they are orthogonal.
2.Linear Independence: We need to show that the vectors u1, u2, and u3 are linearly independent, meaning that no vector can be written as a linear combination of the other vectors.
We can determine linear independence by forming a matrix with the vectors as its columns and performing row operations to check if the matrix can be reduced to the identity matrix.
[A | I] = [u1 | u2 | u3 | I] =
[2 -3 0 | 1 0 0]
[0 0 7 | 0 1 0]
[3 2 0 | 0 0 1]
Performing row operations:
R3 - (3/2)R1 -> R3
R1 <-> R2
[1 0 0 | -3/2 1 0]
[0 1 0 | 0 1 0]
[0 0 7 | 0 0 1]
Since we can obtain the identity matrix on the left side, the vectors u1, u2, and u3 are linearly independent.
Therefore, the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3.
(b) To write v = (1, 2, 3) as a linear combination of u1, u2, and u3, we need to find the coefficients x, y, and z such that:
v = xu1 + yu2 + z*u3
Substituting the given vectors and coefficients:
(1, 2, 3) = x(2, 0, 3) + y(-3, 0, 2) + z(0, 7, 0)
Simplifying the equation component-wise:
1 = 2x - 3y
2 = 7y
3 = 3x + 2y
From the second equation, we can solve for y:
y = 2/7
Substituting y into the first equation:
1 = 2x - 3(2/7)
1 = 2x - 6/7
7 = 14x - 6
14x = 13
x = 13/14
Substituting the found values of x and y into the third equation
3 = 3(13/14) + 2(2/7)
3 = 39/14 + 4/7
3 = 39/14 + 8/14
3 = 47/14
Therefore, we have determined the values of x, y, and z as follows:
x = 13/14
y = 2/7
z = 47/14
Thus, we can write the vector v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) as:
v = (13/14)u1 + (2/7)u2 + (47/14)u3
Therefore, v can be expressed as a linear combination of the given vectors.
Final Answer:Therefore,the linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
To learn more about a vector as a linear combination of vectors using a system of equations from the given link
https://brainly.com/question/30758379
#SPJ4
The linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
To express a vector as a linear combination of vectors using a system of equations, we need to find the coefficients that multiply each given vector to obtain the desired vector. This can be done by setting up a system of equations, where each equation corresponds to the components of the vectors involved.
Body of the Solution:
(a) To show that the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3, we need to demonstrate two conditions: orthogonality and linear independence.
Orthogonality: We need to show that each pair of vectors is orthogonal, meaning their dot product is zero.
u1 · u2 = (2)(-3) + (0)(0) + (3)(2) = -6 + 0 + 6 = 0
u1 · u3 = (2)(0) + (0)(7) + (3)(0) = 0 + 0 + 0 = 0
u2 · u3 = (-3)(0) + (0)(7) + (2)(0) = 0 + 0 + 0 = 0
Since the dot product of every pair of vectors is zero, they are orthogonal.
2.Linear Independence: We need to show that the vectors u1, u2, and u3 are linearly independent, meaning that no vector can be written as a linear combination of the other vectors.
We can determine linear independence by forming a matrix with the vectors as its columns and performing row operations to check if the matrix can be reduced to the identity matrix.
[A | I] = [u1 | u2 | u3 | I] =
[2 -3 0 | 1 0 0]
[0 0 7 | 0 1 0]
[3 2 0 | 0 0 1]
Performing row operations:
R3 - (3/2)R1 -> R3
R1 <-> R2
[1 0 0 | -3/2 1 0]
[0 1 0 | 0 1 0]
[0 0 7 | 0 0 1]
Since we can obtain the identity matrix on the left side, the vectors u1, u2, and u3 are linearly independent.
Therefore, the vectors u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) form an orthogonal basis for R^3.
(b) To write v = (1, 2, 3) as a linear combination of u1, u2, and u3, we need to find the coefficients x, y, and z such that:
v = xu1 + yu2 + z*u3
Substituting the given vectors and coefficients:
(1, 2, 3) = x(2, 0, 3) + y(-3, 0, 2) + z(0, 7, 0)
Simplifying the equation component-wise:
1 = 2x - 3y
2 = 7y
3 = 3x + 2y
From the second equation, we can solve for y:
y = 2/7
Substituting y into the first equation:
1 = 2x - 3(2/7)
1 = 2x - 6/7
7 = 14x - 6
14x = 13
x = 13/14
Substituting the found values of x and y into the third equation
3 = 3(13/14) + 2(2/7)
3 = 39/14 + 4/7
3 = 39/14 + 8/14
3 = 47/14
Therefore, we have determined the values of x, y, and z as follows:
x = 13/14
y = 2/7
z = 47/14
Thus, we can write the vector v = (1, 2, 3) as a linear combination of u1 = (2, 0, 3), u2 = (-3, 0, 2), and u3 = (0, 7, 0) as:
v = (13/14)u1 + (2/7)u2 + (47/14)u3
Therefore, v can be expressed as a linear combination of the given vectors.
Therefore, the linear combination of v = (13/14)u1 + (2/7)u2 + (47/14)u3
Learn more about linear combination
https://brainly.com/question/32297475
#SPJ4
use logarithmic differentiation to find the derivative of y = 3 √x(x −2) / x^2 1 . leave your answer unsimplified.
Answers
To use logarithmic differentiation to find the derivative of y = 3√x(x −2) / x^2, we first take the natural logarithm of both sides:
ln(y) = ln(3√x(x −2) / x^2)
Then we use the logarithmic differentiation rule, which states that if y = f(x) is a function of x, then
y' / y = (ln(f(x)))'
Using this rule, we can find the derivative of ln(y) and simplify it:
ln(y) = ln(3) + (1/2)ln(x(x-2)) - 2ln(x)
ln(y)' = 0 + (1/2)(1/(x(x-2)))(2x-2) - 2*(1/x)
ln(y)' = (x-1)/(x(x-2))
Now we can find y' by multiplying both sides of the original equation by y and substituting in the expression we just found for ln(y)':
y = 3√x(x −2) / x^2
ln(y) = ln(3) + (1/2)ln(x(x-2)) - 2ln(x)
y' / y = (x-1)/(x(x-2))
y' = y*(x-1)/(x(x-2))
Substituting the original expression for y, we have:
y' = (3√x(x −2) / x^2)*((x-1)/(x(x-2)))
Therefore, the derivative of y = 3√x(x −2) / x^2 is y' = (3√x(x −2) / x^2)*((x-1)/(x(x-2))).
To know more about logarithmic differentiation, visit the link given below:
https://brainly.com/question/30766127
#SPJ4
Use distributive property to rewrite expression -8((-2-3/4)-8)
Answers
this is due very soon
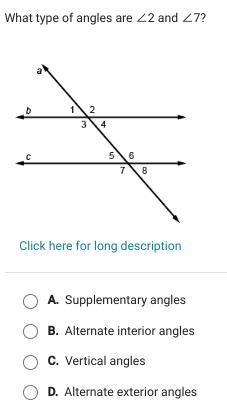
Answers
Answer:
Angles 2 and 7 are opposite exterior angles.
Step-by-step explanation:
Angles 2 and 7 are on the outside so they are exterior, They are also on the opposite sides of the transversal so they are opposite.
Angles 2 and 7 are opposite exterior angles.
How many solutions does the equation -2 + 2y + 3 = 3
a) none
b) one
c) infinity
d) three
Answers
Answer:
one
Step-by-step explanation:
y=1
hope this helps
Answer:
one
Step-by-step explanation:
the quadratic $x^2-3x 1$ can be written in the form $(x b)^2 c$, where $b$ and $c$ are constants. what is $b c$?
Answers
The value of b = -3/2 and c = -5/4
To write the quadratic x² - 3x + 1 in the form (x + b)² + c, we can expand (x + b)² and compare it to the given expression:
(x + b)² = x² + 2bx + b²
Comparing this to the given expression x² - 3x + 1, we see that we need:
2bx = -3x, so b = -3/2
b² + c = 1, so substituting b = -3/2 gives:
(9/4) + c = 1
so c = 1 - 9/4
= 4/4 - 9/4
= -5/4
The quadratic x² - 3x + 1 can be written in the form (x - 3/2)² + ( - 5/4).
Therefore, the value of b = -3/2 and c = -5/4
Learn more about Quadratic Equation here
https://brainly.com/question/30098550
#SPJ4
Given question is incomplete, the complete question is below
the quadratic x²-3x + 1 can be written in the form (x +b)² + c, where b and c are constants. what is b, c?
- 5/6 x 1/8 as decimal
Answers
Answer:
.125
Step-by-step explanation:
Answer:
Im guessing the X is supposed to be multiplication.
-0.10416
Exact Form = -5/48
Step-by-step explanation:
The difference between three times a number and eight equals negative five. What is the number?
6.3
-4.3
-1
1
Answers
Answer:
it's 1
Step-by-step explanation:
when one is multiplied by three times.it gives us three and its difference result negative five 3–8 = -5
Draw the image of quadrilateral ABCD under a translation by 1 unit to the right and 4 units up
Answers
To draw the image of quadrilateral ABCD under a translation by 1 unit to the right and 4 units up, we will move each point of the quadrilateral in the specified direction.
Let's assume the coordinates of the original quadrilateral ABCD are as follows:
A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), D(x₄, y₄)
To perform the translation, we will add the given values to the x-coordinates and y-coordinates of each point:
A'(x₁ + 1, y₁ + 4), B'(x₂ + 1, y₂ + 4), C'(x₃ + 1, y₃ + 4), D'(x₄ + 1, y₄ + 4)
Now, plot the original quadrilateral ABCD and then move each point to its corresponding new position.
For example, if point A had coordinates (2, 3), after the translation, it will move to (2 + 1, 3 + 4) = (3, 7). Similarly, you can calculate the new coordinates for points B, C, and D using the same process.
Once you have the new coordinates for each point, connect them to form the image of the quadrilateral ABCD under the translation.
The new quadrilateral A'B'C'D' will be a shifted version of the original quadrilateral, 1 unit to the right and 4 units up.
It's important to note that the scale and proportions of the quadrilateral will remain the same after the translation. Only its position in the coordinate plane will change.
For more such questions on quadrilateral.
https://brainly.com/question/23935806
#SPJ8
Tyler ate x fruit snacks, and Han 3/4 less than that
Answers
Chanda is planning to visit universities over the summer to help decide where she
wants to attend college. The first two universities on her proposed route are 6
inches apart on Claudias map. In real life, this distance is 30 miles. What scale
does the map use? 1 in = miles.
Answers

Two bags contain white and yellow balls. Bag 1 contains two white balls and four yellow balls. Bag 2 contains four white balls and five yellow balls. A ball is drawn at random from each container. What is the probability that both balls are white?
A. 1/9
B. 1/6
C. 4/27
D. 10/201
Answers
Answer:
C. 4/27
Step-by-step explanation:
Let's use the multiplication rule of probability to calculate the probability that both balls drawn are white:
P(white ball from Bag 1) = 2/6 = 1/3
P(white ball from Bag 2) = 4/9
Therefore, the probability of drawing a white ball from each bag is:
P(white from Bag 1 and white from Bag 2) = P(white from Bag 1) * P(white from Bag 2)
= (1/3) * (4/9)
= 4/27
So, the answer is C. The probability that both balls are white is 4/27.
Lliana started to evaluate the function f(x)=2x^2-3x+7 for the input value 2. What is the value of the function when x=2?
Answers
Answer:it is 9 because you subtract 6 from the 8 and then you add 2 and 7 to get 9
Step-by-step explanation:
If pound of cheese costs $3.43, what is the cost per pound?
PLS HELP
Answers
Answer:
$3.43
Step-by-step explanation:
Cost per pound means how much you are paying for one pound of the item. In this question it says a pound of cheese costs 3.43, therefore each pound of cheese costs 3.43. We can also use the equation 3.43x where x represents the amount of pounds you are purchasing. Just multiply the two and you will get a cost for any amount (pounds) of cheese.
if a franchise company wants to study the relationship between the income of the people living in a neighborhood and the number of sales made at their store in that neighborhood. which statistical method would be best to use in this situation? group of answer choices hypothesis test regression analysis contingency table confidence interval
Answers
The best statistical method to use for studying the relationship between the income of people living in a neighborhood and the number of sales made at the franchise company's store in that neighborhood would be regression analysis.
Regression analysis would be the best statistical method to use in this situation.
It would help to determine the relationship between the income of people living in a neighborhood and the number of sales made at the franchise company's store in that neighborhood.
The regression analysis would provide a model that would help to predict the expected number of sales based on the income levels of the neighborhood.
to learn more about regression analysis click here:
brainly.com/question/28178214
#SPJ11
please help i’ll mark you brainlesttt

Answers
Answer:
Side length = 5 root 2
perimeter is (5 root 2)*3
Step-by-step explanation:
Use pythagoras
a^2 = b^2 + c^2
a^2 = 5 root 2
(5 root 2)^2 = (c^2)/2 + c^2
75 = (c^2)/2 + c^2
150 = c^2 + 2c^2
150 = 3c^2
50=c^2
root of 50 = 5 root 2
as it is equiliateral triangle all sides are the same
Answer:
Side: 10
Perimeter: 30
Step-by-step explanation:
An equilateral triangle has a height of 5√3. What is the length of each side in the equilateral triangle? What is the perimeter of the equilateral triangle?
In triangles with angles with 30°, 60°, and 90°, the hypotenuse (the angle opposite to the 90° angle) is twice as long as the base, and the height is √3 times as long as the base. To make it easier, this is a list of the sides:
x = base
√3 * x = height
2x = hypotenuse.
Look at the drawing I have attached below
If AD is the base of the triangle ADC, then CD, the height is √3 times AD. If we set AD as x, CD = √3*x = 5√3
√3*x = 5√3
Divide both sides by √3.
x = 5
Then, because altitudes in equilateral triangles bisect the base (CD cuts AB in half), then AB = 10.
The sides in equilateral triangles are equal, so each side is 10.
Then, the perimeter must be 30.
I hope this helps! Feel free to ask any questions!

Simplifying algebraic expressions

Answers
Answer:
Step-by-step explanation:
Plug in 5 for h
6(5)+7(5)
30+35=65
65
Answer:
\( \sf \: 6h + 7h = 65\)
Step-by-step explanation:
Given information,
→ 6h + 7h
→ h = 5
Now the final value will be,
→ 6h + 7h
→ 6(5) + 7(5)
→ 30 + 35
→ 65 => final value
Hence, the answer is 65.