how can i tell if an inequality will have a solid line
Answers
The line in a graph of an inequality will be solid if the inequality symbol is ≤ or ≥, or if the inequality is true for all values on both sides of the line.
A solid line in a graph of an inequality means that the values on either side of the line are included in the solution set. To determine if an inequality will have a solid line, you must analyze the inequality symbol.
If the inequality symbol is < or >, then the line will be dashed, indicating that only the values on one side of the line are included in the solution set.
If the inequality symbol is ≤ or ≥, then the line will be solid, indicating that values on both sides of the line are included in the solution set.
For example, consider the inequality x ≥ 0. To graph this inequality, you would draw a line at x = 0. Since the inequality symbol is ≥, you would draw a solid line at x = 0, indicating that the values x = 0 and all values greater than 0 are included in the solution set.
You can also determine if an inequality will have a solid line by solving the inequality. If the inequality is true for all values on both sides of the line, then the line will be solid. For example, consider the inequality x² ≥ 0. Solving this inequality, you get x ≥ 0 and x ≤ 0. Since the inequality is true for all values greater than 0 and all values less than 0, you would draw a solid line at x = 0, indicating that all values of x, including x = 0, are included in the solution set.
The line in a graph of an inequality will be solid if the inequality symbol is ≤ or ≥, or if the inequality is true for all values on both sides of the line.
Learn more about inequality here:
https://brainly.com/question/30231190
#SPJ4
complete question
How can I tell if an inequality will have a solid line?
Related Questions
Let the long-run profit function for a representative firm is given by π i
=p 2
−2p−399, where p is the price of computer. The inverse market demand for computer is given by p=39−0.009q, where q is unit of computers. Suppose technology for producing computers is identical for all firms and all firms face identical input prices. (a) Find the firm's output supply function. (b) Find the market-equilibrium price and the equilibrium number of firms. (c) Find the number of computers sold by each firm in the long run.
Answers
(a) The firm's output supply function is given by q = (p + 199) / 2.
(b) The market-equilibrium price is $32.56, and the equilibrium number of firms is 10.
(c) Each firm sells 70 computers in the long run.
To find the firm's output supply function, we need to maximize the firm's profit function, which is given by π = p^2 - 2p - 399. In the long run, firms will produce where marginal cost equals marginal revenue. Marginal revenue can be obtained by differentiating the inverse market demand function with respect to q, and marginal cost is equal to the derivative of the profit function with respect to q. Equating the two, we get:(39 - 0.009q) = (2q - 2) / q
Simplifying the equation, we find:
q = (p + 199) / 2
This represents the firm's output supply function.
To find the market-equilibrium price and the equilibrium number of firms, we need to find the intersection point of the market demand and supply. Substituting the output supply function into the inverse market demand function, we have:p = 39 - 0.009((p + 199) / 2)
Simplifying and solving for p, we get:
p ≈ $32.56
Substituting this price back into the output supply function, we find:
q = (32.56 + 199) / 2 ≈ 115.78
Given that each firm produces 70 computers in the long run, we can calculate the equilibrium number of firms:
Number of firms = q / 70 ≈ 10
Since each firm sells 70 computers in the long run, and there are 10 firms, the total number of computers sold by each firm is:70 * 10 = 700
Learn more about Equilibrium
brainly.com/question/30694482
#SPJ11
The strength of a rectangular beam varies jointly as its width and the square of its depth. If the strength of a beam 2 inches wide by 10 inches deep is 1000 pounds per square inch, what is the strength of a beam 4 inches wide and 8 inches deep?
Answers
Answer:
yes
Step-by-step explanation:
i know this
PLEASE HELP ME URGENT

Answers
Answer:
Hello! answer: 39
Step-by-step explanation:
Formula for triangles area: base × height ÷ 2
Formula for squares area: base × height
5 × 3 = 15 15 ÷ 2 = 7.5 since there are 4 triangles that are the exact same I will just multiply by 4 so I have all the triangles so 7.5 × 4 = 30 now the square is just 3 × 3 so... 3× 3 = 9 now we add these up 30 + 9 = 39 therefore the surface area is 39
Answer:
39
Step-by-step explanation:
5x3=15
15/2=7.5
7.5x4=30
3x3=9
30+9=39
Sin x = - 1/2
where (-360 < x < 360)
Answers
Answer:
-30, 210 and 330 degrees
Step-by-step explanation:
Given the expression Sin x = - 1/2
x = arcsin(-1/2)
x = -30 degrees
Since sin is negative in the third and fourth quadrant
x = 180 + 30
x = 210 degrees
In the fourth quadrant
x = 360 - 30
x = 330
Hence the value of x within the interval -360 < x < 360 are -30, 210 and 330 degrees
A cylindrical object is 3.13 cm in diameter and 8.94 cm long and
weighs 60.0 g. What is its density in g/cm^3
Answers
A cylindrical object is 3.13 cm in diameter and 8.94 cm long and weighs 60.0 g. The density of the cylindrical object is 0.849 g/cm^3.
To calculate the density, we first need to find the volume of the cylindrical object. The volume of a cylinder can be calculated using the formula V = πr^2h, where r is the radius (half of the diameter) and h is the height (length) of the cylinder.
Given that the diameter is 3.13 cm, the radius is half of that, which is 3.13/2 = 1.565 cm. The length of the cylinder is 8.94 cm.
Using the values obtained, we can calculate the volume: V = π * (1.565 cm)^2 * 8.94 cm = 70.672 cm^3.
The density is calculated by dividing the weight (mass) of the object by its volume. In this case, the weight is given as 60.0 g. Therefore, the density is: Density = 60.0 g / 70.672 cm^3 = 0.849 g/cm^3.
Visit here to learn more about cylindrical:
brainly.com/question/31350681
#SPJ11
Consider the following functions. \[ f(x)=\frac{x}{x+1}, \quad g(x)=\frac{1}{x} \] Find \( (f \circ g)(x) \). Find the domain of \( (f \circ g)(x) \). (Enter your answer using interval notation.) Find
Answers
The domain of \( (f \circ g)(x) \) is all real numbers except \( -1 \), which can be written in interval notation as: \( (-\infty, -1) \cup (-1, \infty) \)
To find \( (f \circ g)(x) \), we need to substitute \( g(x) \) into \( f(x) \).
\( (f \circ g)(x) \) is equal to \( f(g(x)) \), so we need to replace \( x \) in the function \( f(x) \) with \( g(x) \):
\( (f \circ g)(x) = f(g(x)) = f\left(\frac{1}{x}\right) \)
Now let's substitute \( \frac{1}{x} \) into the function \( f(x) \):
\( f\left(\frac{1}{x}\right) = \frac{\frac{1}{x}}{\frac{1}{x}+1} \)
Simplifying the expression, we have:
\( (f \circ g)(x) = \frac{\frac{1}{x}}{\frac{1}{x}+1} \)
To find the domain of \( (f \circ g)(x) \), we need to consider the restrictions on the values of \( x \) that make the expression defined.
In the expression \( (f \circ g)(x) = \frac{\frac{1}{x}}{\frac{1}{x}+1} \), the denominator \( \frac{1}{x}+1 \) should not be equal to zero, as division by zero is undefined.
Setting \( \frac{1}{x}+1 \) not equal to zero, we have:
\( \frac{1}{x}+1 \neq 0 \)
Subtracting 1 from both sides, we get:
\( \frac{1}{x} \neq -1 \)
Taking the reciprocal of both sides, we have:
\( x \neq -\frac{1}{1} \)
Simplifying, we get:
\( x \neq -1 \)
Therefore, the domain of \( (f \circ g)(x) \) is all real numbers except \( -1 \), which can be written in interval notation as:
\( (-\infty, -1) \cup (-1, \infty) \)
Know more about reciprocal here:
https://brainly.com/question/33582378
#SPJ11
10.04 × 8.8= ?
can you help me again please
Answers
Answer:
10.04 × 8.8 =?, ? = 88.352 :)
Answer:
88.352
Step-by-step explanation:
10.04
x. 8.8
=88.352
Triangle TABLE has vertices M(-7,-1) A(5,6) L(2,-3) write the equations of the line that contains the altitude of the triangle that passes through vertex T Brainly
Answers
For the given coordinates the area of the triangle will be 248.5 square units.
What is the equation?An equation is a statement that two expressions, which include variables and/or numbers, are equal. In essence, equations are questions, and efforts to systematically find solutions to these questions have been the driving forces behind the creation of mathematics.
It is given that,triangle TABLE has vertices M(-7,-1) A(5,6) L(2,-3)
x₁,y₁=(-7,-1)
x₂,y₂=(5,6)
x₃,y₃=(2,-3)
We must utilize the triangle's vertices to calculate the area of the triangle in order to obtain the equation,
S=1/2[-7(6-(-3)+5(-3-(-1)+2(-1-(6)]
S=248.5
Thus, for the given coordinates the area of the triangle will be 248.5 square units.
Learn more about the equation here,
https://brainly.com/question/10413253
#SPJ1
Which expression is equivalent to 5(w+4) when w= 9?
519)
9(5)
5(9)+4
O 5(9)+20
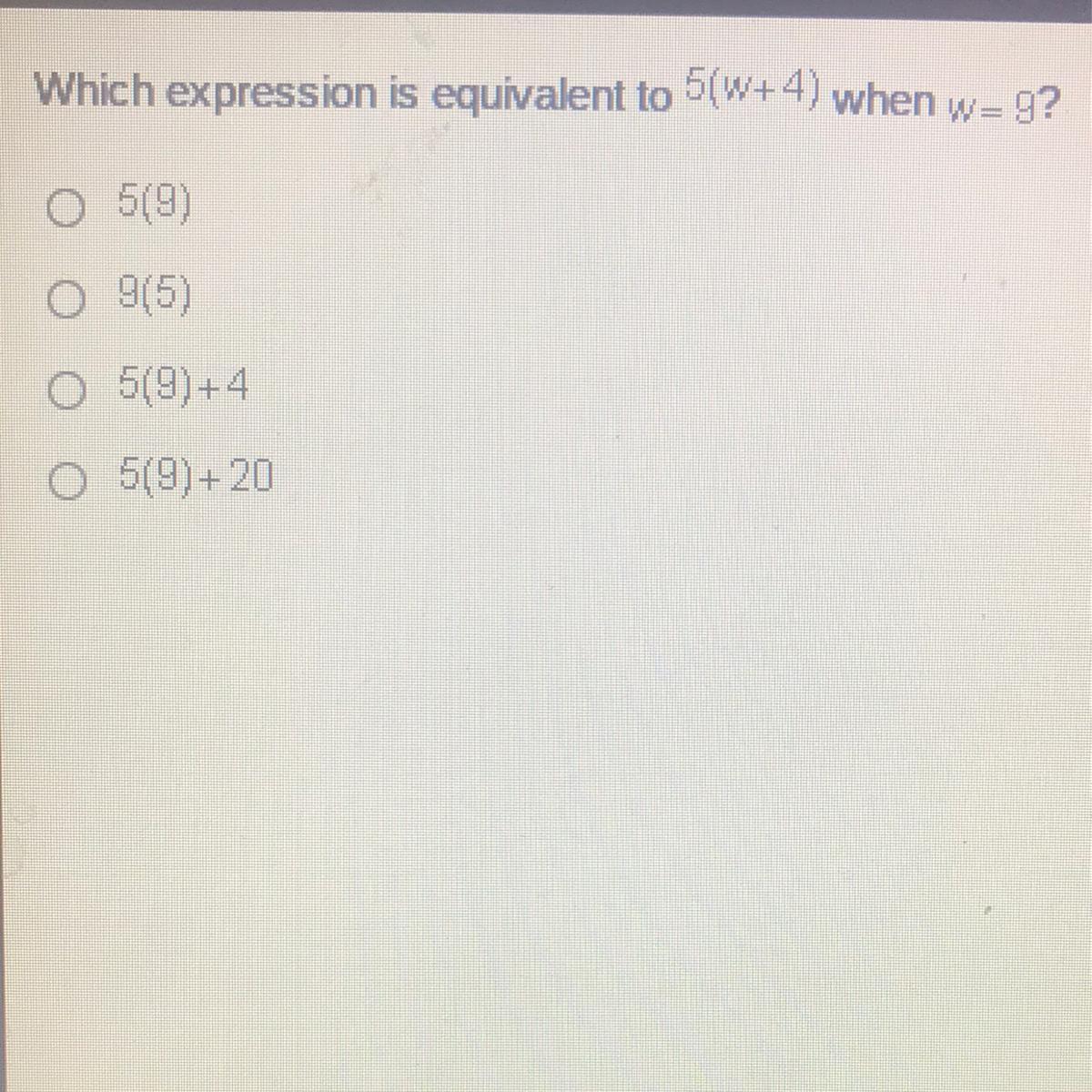
Answers
Answer:
D
Step-by-step explanation:
\(5(9 + 4) \\ 5(13) \\ 65 \\ prove \: it \: d \: answer \\ 5(9) + 20 \\ 45 + 20 \\ = 65\)
which of the following is true about block design? i. the random assignment of units to treatments in a block design is accomplished in groups. ii. a type of block design is matched pairs. iii. the purpose of blocking is to increase variation in results.
Answers
None of the statements you have provided are true about block design.
Here is an explanation of each statement:
i. The random assignment of units to treatments in a block design is not necessarily accomplished in groups. In a block design, units are randomly assigned to treatments within blocks, where a block is a group of units that are similar in some relevant way. For example, if you are conducting an experiment to compare the effectiveness of different fertilizers on plant growth, you might create blocks based on soil type, since different soil types may have different levels of nutrients that could affect plant growth. Within each block, you would then randomly assign the units (plants) to different fertilizers.
ii. Matched pairs is not a type of block design. Matched pairs is a type of experimental design in which pairs of units are matched on some relevant characteristic (e.g., age, gender, weight, etc.), and one member of each pair is randomly assigned to the experimental treatment while the other is assigned to the control.
iii. The purpose of blocking is not to increase variation in results. The purpose of blocking is to control for variables that could affect the outcome of the experiment. By grouping units that are similar in some way, you can reduce the influence of these variables on the results of the experiment. For example, if you are comparing the effectiveness of different fertilizers on plant growth and you have blocks based on soil type, you can be more confident that any differences in plant growth are due to the fertilizers and not to differences in soil type.
Thus, None of the statements you have provided are true about block design.
To learn more about Block Designing,
visit; brainly.com/question/27231083
#SPJ4
Answer:
Random assignment is done SEPARATELY in the blocks/groups.
Matched pair design IS a type of block design.
The purpose of blocking is to DECREASE variation
DOUBLE CHECK
FLVS has different versions of this exact question. All of the above are true. If your question states that blocking is to increase variation, then that option is NOT true - check EVERYTHING. Otherwise you will not get points.
Step-by-step explanation:
Got this correct on the Segment Exam.
Help please! Im on my last question! 15 points.
Question below!

Answers
Answer:
n^2 + 12 = 61
-12 -12
n^2 = 49
Step-by-step explanation:
7 is your answer
7 x 7 = 49 + 12 = 61
4) Find the LCM of 20 and 9
Answers
Answer:
least common multiple is 180
what is 11÷132?? anwser please
Answers
Answer:
11÷132= 0.0833333333
but i think u wanted this answer
132÷11= 12
Combining Like Term
Which of the following expressions are the same? Write 3 sentences to show or explain how you know.
Expression A: 10x - 4x - 4
Expression B: 14x - 4
Expression C: 5x+x-4

Answers
Answer:
Step-by-step explanation:
b
Give the integers p and q such that Nul A is a subspace of Rp and Col A is a subspace of Rq where A is a
(a) 3 x 5 matrix.
(b) 6 x 2 matrix.
(c) 3 x 3 matrix.
Answers
a) We must have p = 5 and q = 3.
b) p = 2 and q = 6.
c) p = q = 3,
a) For a 3 x 5 matrix A, we have A: R^5 → R^3. Since Nul A is a subspace of R^5 and A maps from R^5 to R^3, we must have p = 5 and q = 3.
(b) For a 6 x 2 matrix A, we have A: R^2 → R^6. Since Col A is a subspace of R^6 and A maps from R^2 to R^6, we must have p = 2 and q = 6.
(c) For a 3 x 3 matrix A, we have A: R^3 → R^3. Since Nul A is a subspace of R^3 and Col A is also a subspace of R^3, we can choose either p = q = 3 or p = q = 2. If we choose p = q = 3, then A maps from R^3 to R^3 and both Nul A and Col A are subspaces of R^3. If we choose p = q = 2, then A maps from R^3 to R^2 and we have Nul A as a subspace of R^2 and Col A as a subspace of R^3.
Learn more about subspace here:
https://brainly.com/question/30318872
#SPJ11
Show how to evaluate the functionf(x)= 2e^(4x)-e^(3x)+5e^(x)+1efficiently.Hint: Consider letting z=e^(x)
Answers
The answer to the given question is the function.
f(x)= 2e^(4x)-e^(3x) +5e^(x)+1.
To evaluate the function f(x) = 2e^(4x) - e^(3x) + 5e^(x) + 1 efficiently, we can use the hint given and let z = e^(x). This allows us to simplify the function and make it easier to evaluate.
First, we can substitute z for e^(x) in the function:
f(x) = 2e^(4x) - e^(3x) + 5e^(x) + 1
f(x) = 2z^4 - z^3 + 5z + 1
Now, we can use the distributive property to simplify the function further:
f(x) = 2z^4 - z^3 + 5z + 1
f(x) = z^3(2z - 1) + 5z + 1
Finally, we can evaluate the function by plugging in the value of z:
f(x) = z^3(2z - 1) + 5z + 1
f(x) = e^(3x)(2e^(x) - 1) + 5e^(x) + 1
By using the substitution of z = e^(x), we were able to simplify the function and make it easier to evaluate. This is an efficient way to evaluate the function f(x) = 2e^(4x) - e^(3x) + 5e^(x) + 1.
For more similar questions on substitution:
brainly.com/question/4449154
#SPJ11
Walmart pays $2.50 for a 30 pack of individual chips. They markup the chips by 319%? How much is the 30 pack of chips at Walmart? Include a unit/label with your answer. ROUND TO THE NEAREST CENT
Answers
Answer:
$7.98
Step-by-step explanation:
I am not sure if this is right but hopefully this helps!
Indicate whether (1, 5) is a solution of the given system.
Answers
Answer:
To determine whether (1, 5) is a solution of a given system, you need to substitute these values into the equations of the system and check whether the resulting statements are true.
For example, if the given system is represented by the equations y = 2x + 1 and y = x - 3, then you would substitute 1 for x and 5 for y in each equation and check whether the resulting statements are true.
Substituting these values into the first equation, we get:
5 = 2(1) + 1
5 = 2 + 1
5 = 3
This statement is not true, so (1, 5) is not a solution of this system.
On the other hand, if the given system is represented by the equations y = 2x + 1 and y = 5, then substituting the values (1, 5) into both equations would result in true statements, so (1, 5) would be a solution of this system.
I hope this helps! Let me know if you have any more questions.
Step-by-step explanation:
A skateboarder goes off of a ramp at a speed of 52 ft./s. The ramp is 5 ft. above the ground with a 30°
angle of elevation. Which set of parametric equations represents the skater's jump? The acceleration due
to gravity is 32 ft/s^2.
Answers
The set of parametric equations representing the skater's jump is:
x = 52t
y = 5 + 16t²
We have,
Let's denote the time as t.
Horizontal motion:
The skateboarder's horizontal velocity remains constant throughout the jump, so the horizontal position (x) can be represented as:
x = vt
where v is the horizontal velocity, which in this case is 52 ft/s.
Vertical motion:
The vertical position (y) can be determined using the equations of motion under constant acceleration.
The skateboarder experiences acceleration due to gravity (g) acting downward.
The initial vertical position is 5 ft, and the initial vertical velocity is
0 ft/s.
Using the equation of motion:
\(y = y_0 + vy_0t + 0.5gt^2\)
Substituting the given values:
y = 5 + 0t + 0.5(32)t²
y = 5 + 16t²
Thus,
The set of parametric equations representing the skater's jump is:
x = 52t
y = 5 + 16t²
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ4
Solve the following absolute value inequality. 3x - 727 x < 16 X > [?]
![Solve the following absolute value inequality. 3x - 727 x < 16 X > [?]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/B0bSWamIe1mxhvCDQBcD834x4vPcaO7y.jpeg)
Answers
Answer:
-2
Step-by-step explanation:
3|x-7|<= 27
then |x-7|<=27/3=9
hence, -9<=x-7<=9
therefore, -2<=x<=16
How do
you write 0.4 as a fraction?
Answers
Answer:
Step-by-Step Solution
0.4 = 2/5 as a fraction
To convert the decimal 0.4 to a fraction, just follow these steps:
Step 1: Write down the number as a fraction of one:
0.4 = 0.41
Step 2: Multiply both top and bottom by 10 for every number after the decimal point:
As we have 1 numbers after the decimal point, we multiply both numerator and denominator by 10. So,
0.41 = (0.4 × 10)(1 × 10) = 410.
Step 3: Simplify (or reduce) the above fraction by dividing both numerator and denominator by the GCD (Greatest Common Divisor) between them. In this case, GCD(4,10) = 2. So,
(4÷2)(10÷2) = 2/5 when reduced to the simplest form.
find the value of r so that the line through (2,-3) and (-4,r) has a slope of -1/2 | please explain steps
Answers
Answer:
r = 0
Step-by-step explanation:
slope formula is the difference of the y-values over the difference of the x-values
[r-(-3) / -4-2] = -1/2
r+3/-6 = -1/2
cross-multiply:
2(r+3) = (-1)(-6)
2r + 6 = 6
2r = 0
r = 0
Find the dimensions of a rectangular box of maximum volume suchthat the sum of the lengths of its 12 edges is 30 ft. (Let x, y,and z be the dimensions of the rectangular box.)(x, y, z) = (_______)
Answers
The dimensions of the rectangular box of maximum volume are (5, 5, 5) ft.
To find the dimensions of a rectangular box of maximum volume, we need to use the method of optimization. Let x, y, and z be the dimensions of the rectangular box. The sum of the lengths of its 12 edges is 30 ft, which means:
2x + 2y + 2z = 30
x + y + z = 15
The volume of the rectangular box is given by V = xyz. To find the maximum volume, we need to find the critical point(s) of V. We can use the method of Lagrange multipliers to do this. Let L = xyz + λ(x + y + z - 15), where λ is the Lagrange multiplier.
Taking partial derivatives of L with respect to x, y, z, and λ, we get:
dL/dx = yz + λ = 0
dL/dy = xz + λ = 0
dL/dz = xy + λ = 0
dL/dλ = x + y + z - 15 = 0
Solving these equations, we get:
x = y = z = 5
λ = -25
To learn more about Volume :
https://brainly.com/question/463363
#SPJ11
Solve for x in the equation x squared minus 12 x + 59 = 0.
Answers
Answer:
4 11/12
Step-by-step explanation:
x2−4x−12<0
x2+10x−24<0
x−1=2y
x=−5912
Decimal Form:
x=−4.91¯6
Mixed Number Form:
x=−4 11/12
Answer:
There is no solution to this.
Step-by-step explanation:
Maybe check for a typo?
you would first need to calculate the discriminant, D= b^2-4 a c
D= (-12)^2 -4*1*59
Simplify
D=-92
Since D<0, the quadratic equation has no real solutions.
how to determine if an integral is convergent or divergent
Answers
A. To determine if an integral is convergent, we analyze the function's behavior, integrability, apply integration techniques, and examine its limits, ensuring they are finite, leading to a finite result.
B. To determine if an integral is divergent, we look for infinite limits, vertical asymptotes, and erratic behavior within the integration interval, indicating the lack of a finite value for the integral.
A. To determine if an integral is convergent, we need to consider several approaches. First, we check for basic convergence criteria such as infinite limits or vertical asymptotes.
Then, we examine integrability, ensuring the function is continuous or has a finite number of discontinuities. Next, we simplify the integral using integration techniques.
Finally, we analyze the behavior of the function at infinity and apply comparison tests if necessary to establish convergence.
B. To determine if an integral is divergent, we follow a series of steps. First, we check for basic divergence criteria such as infinite limits or vertical asymptotes.
Then, we examine integrability, looking for discontinuities that prevent integration. Next, we simplify the integral using integration techniques. Finally, if the integral does not converge, it is deemed divergent.
for such more question on convergence
https://brainly.com/question/23558817
#SPJ8
"Another name for Phase 5: Systems Implementation is ________.
A) Feasibility
B) Conversion
C) Analysis
D) Development"
Answers
Phase 5: The system of implementation is conversion.
Option B is the correct answer.
We have,
Phase 5 of the system development life cycle is commonly referred to as "Conversion" or "Systems Implementation."
During this phase,
The focus shifts from planning and designing the system to actually implementing it.
This phase involves the conversion of the old system to the new system, which includes activities such as data conversion, software installation, hardware setup, user training, and system testing.
The term "Conversion" is used because it signifies the transition from the old system to the new system.
It involves migrating data, processes, and operations from the existing system to the new system.
This phase ensures that the newly developed system is successfully integrated into the organization and becomes fully operational.
Thus,
Phase 5: The system of implementation is conversion.
Learn more about the system of implementations here:
https://brainly.com/question/30569936
#SPJ1
Consider the multivariable function f\left(x,y,z\right)=\frac{x^3-2.5y^2+\frac{z}{2}}{z\left(x-y\right)}f ( x , y , z ) = x 3 − 2.5 y 2 + z 2 z ( x − y ). Evaluate f\left(2,3,1\right)f ( 2 , 3 , 1 ). Round your answer to two decimal places.
Answers
Answer:
\(f\left(2,3,1\right)=\bold{14}\)
Step-by-step explanation:
Given the function:
\(f\left(x,y,z\right)=\frac{x^3-2.5y^2+\frac{z}{2}}{z\left(x-y\right)}\)
To find:
The value of \(f(2, 3, 1)\) = ?
Solution:
\(f(2, 3, 1)\) means the values of \(x, y\ and\ z\) as:
\(x=2\\y=3\\z=1\)
Let us put the given values in the given function and let us solve for it:
\(\Rightarrow f\left(2,3,1\right)=\dfrac{2^3-2.5\times 3^2+\frac{1}{2}}{1\left(2-3\right)}\\\\\Rightarrow f\left(2,3,1\right)=\dfrac{8-2.5\times 9+0.5}{1\left(-1\right)}\\\\\Rightarrow f\left(2,3,1\right)=\dfrac{8-22.5+0.5}{-1}\\\\\Rightarrow f\left(2,3,1\right)=\dfrac{-14}{-1}\\\\\Rightarrow f\left(2,3,1\right)=\bold{14}\)
Therefore, the answer is:
\(f\left(2,3,1\right)=\bold{14}\)
Use the equation y+5=x4 to fill in the missing values in the table below
heeeeeeeeeelllllllllppppppppppp pleeaaassseee

Answers
Answer:
hope this helps
Step-by-step explanation:
1.-2
2.-5
3.20
4.-12
The missing values in the relationship given are :
43-5-5/4-3/4Given the equation :
y + 5 = 4x
Value of y when x = 12 :
Put x = 12 in the equation :
y + 5 = 4(12)
y + 5 = 48
y = 48 - 5
y = 43
Value of y when x = 0
Put x = 0 in the equation :
y + 5 = 4(0)
y + 5 = 0
y = 0 - 5
y = - 5
Value of x when y = 0
Put y = 0 in the equation :
0 + 5 = 4x
-5 = 4x
Divide both sides by 4
-5/4 = x
Value of x when y = - 8
Put y = - 8 in the equation :
-8 + 5 = 4x
-3= 4x
Divide both sides by 4
-3/4= x
The missing values are : 43, - 5, - 5/4 and - 3/4
Learn more : https://brainly.com/question/18112348
What is the completely factored form of this polynomial?
– 8x²+
+ 16
Answers
Answer:
-8(x²-2)
Step-by-step explanation:
Factor -8 out of -8x²
-8(x²)+16
Factor -8 out of 16.
-8(x²)-8(-2)
Factor -8 out of -8(x²)-8(-2).
Instructions: Find the value of the trigonometric ratio. Make sure to simplify the fraction if
needed.

Answers
Step-by-step explanation:
\( \sin(x) = \frac{12}{13} \)
The value of the trigonometric ratio are; \(\sin(x) = \dfrac{\text{12}}{\text{13}}\).
On which triangle can we apply trigonometric ratios?Trigonometric ratio can be defined in terms of ratios of perpendicular, bases and hypotenuse.
Trigonometric ratio are defined only in right angled triangles (triangles whose one angle is of 90 degree measure).
Trigonometric ratios for a right angled triangle are from the perspective of a particular non-right angle.
In a right angled triangle, two such angles are there which are not right angled(not of 90 degrees).
From the considered angle, the side opposite to it is called perpendicular, and the remaining side will be called base.
From that angle suppose its measure is θ,
\(\sin(\theta) = \dfrac{\text{Length of perpendicular}}{\text{Length of Hypotenuse}}\)
\(\sin(x) = \dfrac{\text{12}}{\text{13}}\)
Therefore, The value of the trigonometric ratio are; \(\sin(x) = \dfrac{\text{12}}{\text{13}}\).
Learn more about trigonometric ratios here:
https://brainly.com/question/22599614
#SPJ2