Hiro has 5 kilog of potatos a 2 kg of onions he plans to use 3. 25 kg of potatoes and 550 grams of onions for recipe. How many total kilograms of the produce will not be used?
Answers
Hiro will not use a total weight of 3.2 kg of production for 5 kilos of potatoes a 2 kg of onions he plans to use 3.
To find out how many total kilograms of produce Hiro will not use, we need to subtract the number of potatoes and onions he will use for the recipe from the total amount he has. Here's how we can approach the problem:
First, we need to convert 550 grams of onions to kilograms by dividing by 1000:
550 g ÷ 1000 = 0.55 kg
Now we can add up the number of potatoes and onions Hiro will use for the recipe:
3.25 kg (potatoes) + 0.55 kg (onions) = 3.8 kg
Next, we can subtract the amount of produce used from the total amount Hiro has:
5 kg (potatoes) + 2 kg (onions) - 3.8 kg (produce used) = 3.2 kg
Learn more about the weight of production at
https://brainly.com/question/21273553
#SPJ4
Related Questions
find the missing side length.

Answers
Use the formula shown:
6^2 + 2.5^ = c^2
36 + 6.25 = c^2
42.25 = c^2
Take the square root of both sides:
c = 13/2 as a fraction or 2.5495 as a decimal (round off as needed)
2 Which Venn diagram shows the correct relationship among different sets of numbers and the
correct placement of -648?
Integers
Whole
numbers
-648
-648
F
Whole
numbers
H
Integers
Rational numbers
Rational numbers
Integers
Whole
numbers
J
Whole
numbers
-648
Integers
-648
Rational numbers
Rational numbers
Answers
The Venn diagram shows the correct relationship among different sets of numbers and the correct placement of -648 is (f) rational number , integer (-648) and whole number
Whole number the numbers without fractions and it is a collection of positive integers and zero.
-648 is not a whole number because it is negative.
Integers is a whole number that can be positive, negative, or zero
Integers can be negative so -648 is an integer
Rational number any number that can be written as a fraction, where both the numerator (the top number) and the denominator (the bottom number) are integers, and the denominator is not equal to zero.
Rational includes integer and whole number.
To know more about Venn diagram click here :
https://brainly.com/question/29301560
#SPJ4
The given question is incomplete the complete question is :
Which Venn diagram shows the correct relationship among different sets of numbers and the correct placement of -648?

100 points! WILL GIVE BRAINLIST FOR FIRST ANSWER
A building covers an area of 600 square ft. the eight is 45 feet what is the volume?
Answers
Answer:
27000
Step-by-step explanation:
600(45)=27000
Answer:
27000
Step-by-step explanation:
Find the square root of the following decimal numbers.
(b) 0.0016
Answers
The square root of the decimal number is √0.0016 = 0.04
How to find the square root of the decimal number?Here we can find the square root of the decimal number:
N = 0.0016
Notice that we can write this number as:
0.0016 = 16*10⁻⁴
Now we can take the square root of that, so we will get:
√(16*10⁻⁴)
We can distribute the square root to get:
√16*√10⁻⁴
These two are easy, we will get:
√16*√10⁻⁴ = 4*10⁻² = 0.04
That is the square root.
Learn more about square roots at:
https://brainly.com/question/428672
#SPJ1
A moving company drove one of its trucks 100,042 miles one year. A second truck was driven 98,117 miles, and a third truck was driven 120,890 miles. How many miles were driven by all three trucks?
Answers
What is the mode for the month?
A) 22
B) 20
C) 21
D) 20.4

Answers
Math help
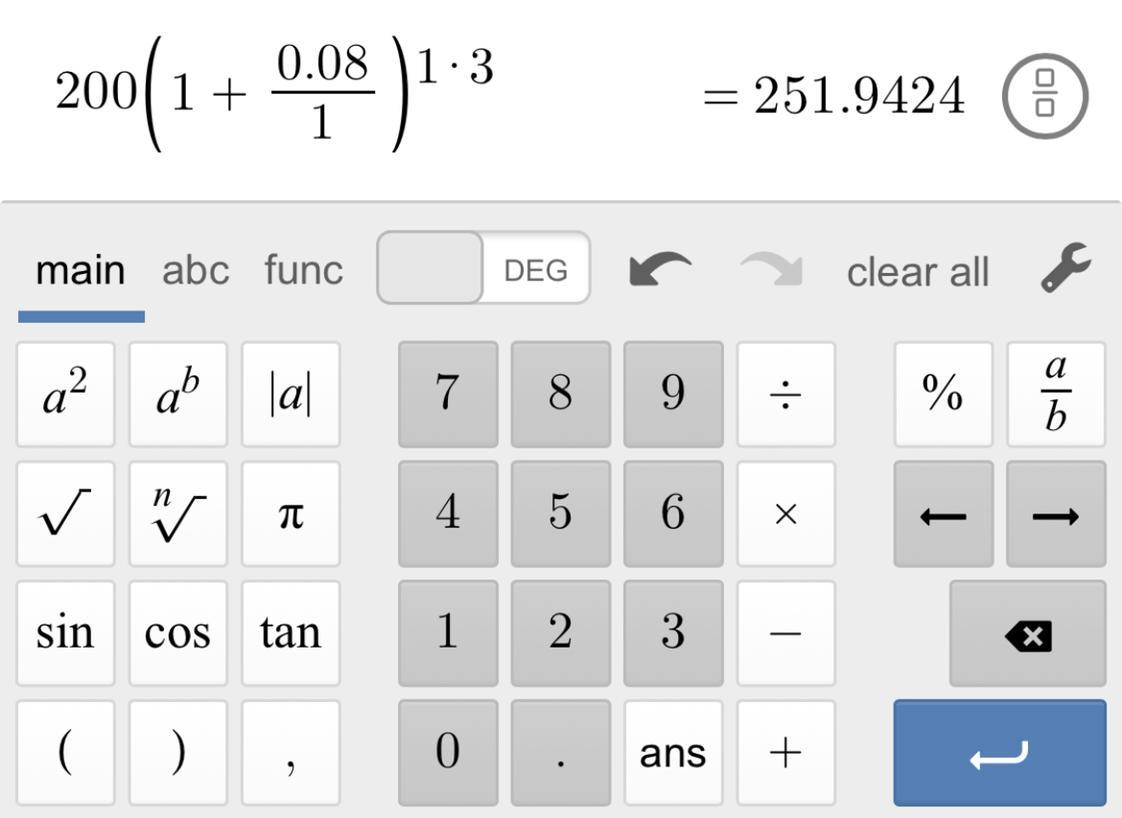
Sally puts $200.00 in a bank account. This account
earns 8% compound interest. How much money is
in the account after three years?
Answers
Answer:
B $240.00
Step-by-step explanation:
thats the correct answer
Use A=P(1+r/n)^nt to solve!
A = Amount after time
P = Initial value
t = Time in years
r = Rate
n = Number of compounds(¿?)
A=200(1+0.08/1)^1x3
There is $251.94 in the account after three years!
Find the slope of the line passing through the points (-6, -5) and (4,4).
Answers
Answer:
9/10 or 0.9
Step-by-step explanation:
Slope of a line passing through two points (x1, y1) and (x2, y2) is given by
Slope m = rise/run
where
rise = y2 - y1
run = x2 - x1
Given points (- 6, - 5) and (4, 4),
rise = 4 - (-5) = 4 + 5 = 9
run = 4 - ( - 6) = 4 + 6 = 10
Slope = rise/run = 9/10 or 0.9
4
2
▸
Which number completes the system of linear
inequalities represented by the graph?
y22x-2 and x + 4y2-12v
-12
-3
4
6
Answers
The complete system of linear inequalities represented by the graph is y ≥ 2x – 2 and x + 4y ≥ -12.
What is inequality?A mathematical phrase in which the sides are not equal is referred to as being unequal. In essence, a comparison of any two values reveals whether one is less than, larger than, or equal to the value on the opposite side of the equation.
As per the given graph.
The inequality y ≥ 2x – 2 is represented by the red line.
The blue line goes from (0,-3) so it must satisfy the inequality.
Thus, 0 + 4(-3) = -12
Thus, x + 4y ≥ -12 will be the inequality.
Hence "The complete system of linear inequalities represented by the graph is y ≥ 2x – 2 and x + 4y ≥ -12".
For more about inequality,
brainly.com/question/20383699
#SPJ1
The given question is incomplete, the complete question follows,
Which number completes the system of linear inequalities represented by the graph?
y >= 2x – 2 and x + 4y >= ?

Need help on this! Please someone help!!!

Answers
This can be easily solved, especially with a calculator.
With the calculator, you can find that \(\sqrt{42}\) is about 6.4807.
Multiply that by 2, you get about 13 inches.
If you can't use a calculator, then you can just estimate. Since we know that \(\sqrt{36}\) is 6 and \(\sqrt{49}\) is 7, \(\sqrt{42}\) is in between them, so you can just say somewhere around 6.5.
Multiply 2 * 6.5 and you get 13 inches.
Dominic is shopping at a store that is offering a discount of 15%, percent off the usual price of any item. 1. Write an equation that represents the amount of discount offered (d) on an item whose usual price is p. 2. How much discount does Dominic receive on an item whose usual price is pounds 80pounds,
Answers
Dominic receives 12 pounds on an item whose usual price is 80 pounds
Write an equation that represents the amount of discount offered (d) on an item whose usual price is p.The given parameters are:
Discount =15%
Price = p
Amount of discount = d
The equation that represents the amount of discount offered (d) on an item whose usual price is p is
d = Discount * p
This gives
d = 15% * p
Evaluate
d = 0.15p
How much discount does Dominic receive on an item whose usual price is 80 pounds,In (a), we have
d = 0.15p
Here, p = 80
So, we have
d = 0.15 * 80
Evaluate
d = 12
Hence, Dominic receives 12 pounds on an item whose usual price is 80 pounds
Read more about discounts at:
https://brainly.com/question/7459025
#SPJ1
Answer:
If the store is offering a discount of 15% off the usual price
the equation is \(D=0.15p\)
Dominic gets a £12
discount on an item whose usual price i
The dimension of the row space of a 3 x 3 matrix A is 2. (a) What is the dimension of the column space of A? (b) What is the rank of A? (c) What is the nullity of A? (d) What is the dimension of the solution space of the homogeneous system Ax = 0?
Answers
a) the dimension of its column space is also 2. b) the rank of A is 2. c) the nullity of matrix A is 1. d) the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
(a) The dimension of the row space of a matrix is equal to the dimension of its column space. So, if the dimension of the row space of matrix A is 2, then the dimension of its column space is also 2.
(b) The rank of a matrix is defined as the maximum number of linearly independent rows or columns in the matrix. Since the dimension of the row space of matrix A is 2, the rank of A is also 2.
(c) The nullity of a matrix is defined as the dimension of the null space, which is the set of all solutions to the homogeneous equation Ax = 0. In this case, the matrix A is a 3 x 3 matrix, so the nullity can be calculated using the formula:
nullity = number of columns - rank
nullity = 3 - 2 = 1
Therefore, the nullity of matrix A is 1.
(d) The dimension of the solution space of the homogeneous system Ax = 0 is equal to the nullity of the matrix A. In this case, we have already determined that the nullity of matrix A is 1. Therefore, the dimension of the solution space of the homogeneous system \(A_x = 0\) is also 1.
Know more about matrix here:
brainly.com/question/24079385
#SPJ4
#2 A student wants to determine if the proportion of times a spun penny lands on heads is different from 0.5. She spins a penny 50 times and records the number of times it lands on heads.
What is the appropriate inference procedure?
one-sample t-test for μ
one-sample z-test for p
one-sample t-test for diff
two-sample z-test for Pâ-Pâ
Answers
The appropriate inference procedure is a one-sample z-test for p.
A one-sample z-test for the percentage would be the proper inference method in this case.
This is due to the fact that we only have one sample of coin flips and wish to determine whether the population's genuine percentage of heads (p), which represents the proportion of heads in the population, differs substantially from 0.5 (our null hypothesis).
In a one-sample z-test for the percentage, the sample proportion (p-hat) is calculated, and the standard error formula is used to get a z-statistic, which is then compared to a normal distribution to provide a p-value.
If the p-value is less than the significance level, which is typically 0.05, the null hypothesis is rejected.
To learn more about the z-test;
https://brainly.com/question/30998088
#SPJ1
Carbon-14 Dating Skeletal remains had lost 70% of the C-34 they only contained. Determine the approximate apen years of the bones. (Assume the art of carbon 10 is 5730 years Round your answer to the nearest whole number
Answers
Carbon-14 Dating Skeletal remains that had lost 70% of the C-14 they initially contained need to be evaluated for their age.
To approximate the age of the bones, carbon-14 dating method is used.
Carbon-14 dating is a technique used to determine the age of an artifact containing organic material by measuring the amount of carbon-14 remaining in the sample. C-14 is formed in the atmosphere when neutrons from cosmic radiation interact with nitrogen atoms.
When a living organism dies, it stops taking in carbon-14, and the carbon-14 it contains starts to decay into nitrogen-14 at a steady rate. So the remaining amount of C-14 can be used to determine the age of the sample.
Carbon-14 has a half-life of about 5730 years which means that after 5730 years, half of the initial amount of C-14 will remain in the sample. The time elapsed for the decay of a radioactive substance to half of its initial amount is known as its half-life.
Therefore, if an organism had 100 units of C-14 when it died, it would have 50 units of C-14 after 5730 years, 25 units of C-14 after 11,460 years, and so on.
To determine the approximate age of the bones, we use the following formula:
Amount of C-14
Remaining = Initial amount of C-14 x (0.5)^(t/h)where t is the time elapsed and h is the half-life of carbon-14.
The skeletal remains had lost 70% of the C-14 they only contained.
Therefore, the remaining amount of C-14 is 30% or 0.30 of the initial amount of C-14.
Therefore,
Amount of C-14
Remaining = 0.30 x Initial amount of C-14
Putting this value in the formula we get,0.30 x Initial amount of C-14 = Initial amount of C-14 x (0.5)^(t/h
)Dividing by Initial amount of C-14 on both sides we get,0.30 = 0.5^(t/h)
Taking natural logarithm on both sides we get,
ln 0.30 = (t/h) ln 0.5
Solving for t, we get,
t = (ln 0.30)/(ln 0.5 x h)t = (ln 0.30)/(ln 0.5 x 5730)≈ 11,113
Therefore, the bones are approximately 11,113 years old. Rounding this to the nearest whole number, the approximate age of the bones is 11,113 years.
To know more about Carbon-14 visit:
https://brainly.com/question/15721348
#SPJ11
School is 2 miles from home along a straight road. The table shows your distance from home as you walk home at a constant rate.
Time (min)
10
20
30
Distance from home (miles)
1.5
1
0.5
Is the relationship in the table proportional?
Find your distance from school for each time in the table.
Write an equation representing the relationship between the distance from school and time walking.
Answers
oliver sewed a quilt 3 2/3 feet long and 2 1/4 feet wide. what is the area of her quilt?
Answers
Answer:
8.25 feet
Step-by-step explanation:
3 2/3 times 2 1/4 equals 8.25
Use the graph above to identify the corresponding y-value for each given x-value.
1. x=2, y =
2. x = -3, y =
3. x = 1, y =
4. x = 0, y =

Answers
Answer:
Step-by-step explanation:
4 is the answer
which is the equation of a parabola with focus (0 5) and directrix y=-5
Answers
The equation of parabola will be x^2 = 20y.
The given focus is (0, 5) and the given directrix is y = -5.
Let (x, y) be any point on the parabola.
The distance from (x, y) to the focus (0, 5) is given by:
sqrt((x-0)^2 + (y-5)^2)
The distance from (x, y) to the directrix y = -5 is simply |y - (-5)| = |y + 5|
By definition of a parabola, these distances are equal. Therefore, we have:
sqrt((x-0)^2 + (y-5)^2) = |y + 5|
Squaring both sides, we get:
\((x-0)^{2} + (y-5)^{2} = (y + 5)^{2}\)
Simplifying and rearranging, we get:
\(x^{2}\) = 4(5)y
Therefore, the equation of the parabola with focus (0, 5) and directrix y = -5 is:
\(x^{2}\) = 20y.
To know more about equation of a parabola refer here:
https://brainly.com/question/28122787?#
SPJ11
6. Ainsley invests in a bank account that
earns interest compounded yearly.
The expression 680(1.031) can be
used to find the account balance in
t years.
Part A
What was Ainsley's initial
investment?
$
Answers
Ainsley's initial investment was approximately $660.184.
How to determine Ainsley's initial investmentLet's denote Ainsley's initial investment as x.
The expression 680(1.031) represents the account balance after one year, given that the initial investment of x earns an interest rate of 3.1% (or 0.031 in decimal form) compounded yearly.
So, we can set up the equation:
x(1.031) = 680
To solve for x, we need to divide both sides of the equation by 1.031:
x = 680 / 1.031
Evaluating the expression:
x ≈ 660.184
Therefore, Ainsley's initial investment was approximately $660.184.
Learn more about expression at https://brainly.com/question/1859113
#SPJ1
1. Find an equivalent ratio to 12:9 such that the second number is 3.
O a. 6:3
O b. 4:3
O c. 9:3
Answers
Answer:
B. 4:3
Step-by-step explanation:
Divide both by 3:
12/3 = 4
9/3 = 3
4:3
Solve for hhh.
\dfrac{h}6-1 = -3
6
h
−1=−3start fraction, h, divided by, 6, end fraction, minus, 1, equals, minus, 3
h =h=h, equals
Answers
The value of the variable h in the given fraction problem (h/6) - 1 = -3 is; h = -12
How to Solve Fraction Problems?
We are given the fraction problem as (h/6) - 1 = -3
Now, from this given fraction problem, the first step will be to rearrange the equation by adding 1 to both sides to get;
(h/6) - 1 + 1 = -3 + 1
(h/6) = -2
Now, the next step will be to multiply both sides by 6 to get;
(h/6) * 6 = -2 * 6
h = -12
Read more about Solving Fraction at; https://brainly.com/question/11562149
#SPJ1
Complete question is;
Solve for h if (h/6) - 1 = -3
Solve the differential equation y
′′
+
2
y
′
+
y
=
e
−
2
t
ln
t
by variation of parameters.
Answers
Answer:
\(y(t)=c_1e^{-t}+c_2te^{-t}+\frac{1}{2}t^2\ln(t)e^{-t}-\frac{3}{4} t^2e^{-t}\)
Step-by-step explanation:
Given the second-order differential equation. Solve by using variation of parameters.
\(y''+2y'+y=e^{-t}\ln(t)\)
(1) - Solve the DE as if it were homogeneous to find the homogeneous solution
\(y''+2y'+y=e^{-t}\ln(t) \Longrightarrow y''+2y'+y=0\\\\\text{The characteristic equation} \rightarrow m^2+2m+1=0, \ \text{solve for m}\\\\m^2+2m+1=0\\\\\Longrightarrow (m+1)(m+1)=0\\\\\therefore \boxed{m=-1,-1}\)
\(\boxed{\left\begin{array}{ccc}\text{\underline{Solutions to Higher-order DE's:}}\\\\\text{Real,distinct roots} \rightarrow y=c_1e^{m_1t}+c_2e^{m_2t}+...+c_ne^{m_nt}\\\\ \text{Duplicate roots} \rightarrow y=c_1e^{mt}+c_2te^{mt}+...+c_nt^ne^{mt}\\\\ \text{Complex roots} \rightarrow y=c_1e^{\alpha t}\cos(\beta t)+c_2e^{\alpha t}\sin(\beta t)+... \ ;m=\alpha \pm \beta i\end{array}\right}\)
Notice we have repeated/duplicate roots, form the homogeneous solution.
\(\boxed{\boxed{y_h=c_1e^{-t}+c_2te^{-t}}}\)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Now using the method of variation of parameters, please follow along very carefully.
\(\boxed{\left\begin{array}{ccc}\text{\underline{Variation of Parameters Method(1 of 2):}}\\ \text{Given a DE in the form} \rightarrow ay''+by"+cy=g(t) \\ \text{1. Obtain the homogenous solution.} \\ \Rightarrow y_h=c_1y_1+c_2y_2+...+c_ny_n \\ \\ \text{2. Find the Wronskain Determinant.} \\ |W|=$\left|\begin{array}{cccc}y_1 & y_2 & \dots & y_n \\y_1' & y_2' & \dots & y_n' \\\vdots & \vdots & \ddots & \vdots \\ y_1^{(n-1)} & y_2^{(n-1)} & \dots & y_n^{(n-1)}\end{array}\right|$ \\ \\ \end{array}\right}\)
\(\boxed{\left\begin{array}{ccc}\text{\underline{Variation of Parameters Method(2 of 2):}}\\ \text{3. Find} \ W_1, \ W_2, \dots, \ W_n.\\ \\ \text{4. Find} \ u_1, \ u_2, \dots, \ u_n. \\ \Rightarrow u_n= \int\frac{W_n}{|W|} \\ \\ \text{5. Form the particular solution.} \\ \Rightarrow y_p=u_1y_1+u_2y_2+ \dots+ u_ny_n \\ \\ \text{6. Form the general solution.}\\ y_{gen.}=y_h+y_p\end{array}\right}\)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
(2) - Finding the Wronksian determinant
\(|W|= \left|\begin{array}{ccc}e^{-t}&te^{-t}\\-e^{-t}&e^{-t}-te^{-t}\end{array}\right|\\\\\Longrightarrow (e^{-t})(e^{-t}-te^{-t})-(te^{-t})(-e^{-t})\\\\\Longrightarrow (e^{-2t}-te^{-2t})-(-te^{-2t})\\\\\therefore \boxed{|W|=e^{-2t}}\)
(3) - Finding W_1 and W_2
\(W_1=\left|\begin{array}{ccc}0&y_2\\g(t)&y_2'\end{array}\right| \ \text{Recall:} \ g(t)=e^{-t} \ln(t)\\\\\Longrightarrow \left|\begin{array}{ccc}0&te^{-t}\\e^{-t} \ln(t)&e^{-t}-te^{-t}\end{array}\right|\\\\\Longrightarrow 0-(te^{-t})(e^{-t} \ln(t))\\\\\therefore \boxed{W_1=-t\ln(t)e^{-2t}}\)
\(W_2=\left|\begin{array}{ccc}y_1&0\\y_1'&g(t)\end{array}\right| \ \text{Recall:} \ g(t)=e^{-t} \ln(t)\\\\\Longrightarrow \left|\begin{array}{ccc}e^{-t}&0\\-e^(-t)&e^{-t} \ln(t)\end{array}\right|\\\\\Longrightarrow (e^{-t})(e^{-t} \ln(t))-0\\\\\therefore \boxed{W_2=\ln(t)e^{-2t}}\)
(4) - Finding u_1 and u_2
\(u_1=\int \frac{W_1}{|W|}; \text{Recall:} \ W_1=-t\ln(t)e^{-2t} \ \text{and} \ |W|=e^{-2t} \\\\\Longrightarrow \int\frac{-t\ln(t)e^{-2t}}{e^{-2t}} dt\\\\\Longrightarrow -\int t\ln(t)dt \ \text{(Apply integration by parts)}\\\\\\\boxed{\left\begin{array}{ccc}\text{\underline{Integration by Parts:}}\\\\uv-\int vdu\end{array}\right }\\\\\text{Let} \ u=\ln(t) \rightarrow du=\frac{1}{t}dt \\\\\text{an let} \ dv=tdt \rightarrow v=\frac{1}{2}t^2 \\\\\)
\(\Longrightarrow -\Big[(\ln(t))(\frac{1}{2}t^2)-\int [(\frac{1}{2}t^2)(\frac{1}{t}dt)]\Big]\\\\\Longrightarrow -\Big[\frac{1}{2}t^2\ln(t)-\frac{1}{2}\int (t)dt\Big]\\\\\Longrightarrow -\Big[\frac{1}{2}t^2\ln(t)-\frac{1}{2}\cdot\frac{1}{2}t^2 \Big]\\\\\therefore \boxed{u_1=\frac{1}{4}t^2-\frac{1}{2}t^2\ln(t)}\)
\(u_2=\int \frac{W_2}{|W|}; \text{Recall:} \ W_2=\ln(t)e^{-2t} \ \text{and} \ |W|=e^{-2t} \\\\\Longrightarrow \int\frac{\ln(t)e^{-2t}}{e^{-2t}} dt\\\\\Longrightarrow \int \ln(t)dt \ \text{(Once again, apply integration by parts)}\\\\\text{Let} \ u=\ln(t) \rightarrow du=\frac{1}{t}dt \\\\\text{an let} \ dv=1dt \rightarrow v=t \\\\\Longrightarrow (\ln(t))(t)-\int[(t)(\frac{1}{t}dt )] \\\\\Longrightarrow t\ln(t)-\int 1dt\\\\\therefore \boxed{u_2=t \ln(t)-t}\)
(5) - Form the particular solution
\(y_p=u_1y_1+u_2y_2\\\\\Longrightarrow (\frac{1}{4}t^2-\frac{1}{2}t^2\ln(t))(e^{-t})+(t \ln(t)-t)(te^{-t})\\\\\Longrightarrow\frac{1}{4}t^2e^{-t}-\frac{1}{2}t^2\ln(t)e^{-t}+ t^2\ln(t)e^{-t}-t^2e^{-t}\\\\\therefore \boxed{ y_p=\frac{1}{2}t^2\ln(t)e^{-t}-\frac{3}{4} t^2e^{-t}}\)
(6) - Form the solution
\(y_{gen.}=y_h+y_p\\\\\therefore\boxed{\boxed{y(t)=c_1e^{-t}+c_2te^{-t}+\frac{1}{2}t^2\ln(t)e^{-t}-\frac{3}{4} t^2e^{-t}}}\)
Thus, the given DE is solved.

Eli runs 5 meters per second.
On a coordinate plane, a line goes through points (1, 5) and (2, 10)..
Use the graph to identify the independent and the dependent variable. Check all that apply.
The two variables are Eli and 5.
The two variables are meters and seconds.
Meters are graphed on the x-axis.
Meters are graphed on the y-axis.
Seconds is the independent variable.
Seconds is the dependent variable.
Answers
Answer:
the two variables are meters and seconds,. meters are graphed on the y- axis, seconds is the independent variable....2,4,5
Answer:
right answer lol
Step-by-step explanation:

He park trail is 10x^2+4x+2 miles long. The hiker has traveled 5x-1 miles. How much farther does the hiker need to travel to get to the end of the trail
Answers
Answer:
\(10x^2-x+3\) miles.
Step-by-step explanation:
It is given that,
Total length of park trail = \(10x^2+4x+2\) miles
Total length traveled by hiker = \(5x-1\) miles
We need to find the length of trail hiker need to travel to get to the end of the trail.
Required length \(=10x^2+4x+2-(5x-1)\)
\(=10x^2+4x+2-5x+1\)
\(=10x^2+(4x-5x)+(2+1)\)
\(=10x^2-x+3\)
Therefore, hiker need to travel \(10x^2-x+3\) miles to get to the end of the trail.
A man bought a car for 5500 cedis and sold it for 6500 cedis .find the percentage gain
Answers
Answer:
Around 18.18%
Step-by-step explanation:
We can use the percentage increase formula to find the gain here. The formula goes:
\(\frac{new-original}{original}\cdot100\).
We know that the new value is 6500, and the old value is 5500, so we can substitute inside the equation.
\(\frac{6500-5500}{5500}\cdot100\\\\\frac{1000}{5500}\cdot100 \\\\0.\overline{18} \cdot100\\\\18.\overline{18}\)
Which rounds to 18.18%.
Hope this helped!
Calculate the expected value of the scenario.xP(x;)- $1.250.1- $0.250.4$00.2$1.250.3 (Expected value = $ “ANSWER”)

Answers
The Expected Value of a Discrete Probability Distribution
Given a number of events:
x = {x1, x2, x3,..., xn}
And their respective probabilities:
P = {p1, p2, p3,..., pn}
The expected value is calculated as follows:
\(Ex=\sum ^{i=n}_{i=1}x_i\cdot p_i\)We are given:
x = {-1.25, -0.25, 0, 1.25}
P = {0.1, 0.4, 0.2, 0.3}
Substituting:
\(Ex=(-1.25)\cdot0.1+(-0.25)\cdot0.4+(0)\cdot0.2+(1.25)\cdot0.3\)Calculating:
\(\begin{gathered} Ex=-0.125-0.1+0+0.375 \\ Ex=0.15 \end{gathered}\)The expected value is $0.15
A bookstore sells cookbooks, novels and reference books. The ratio of the number of
cookbooks to the number of novels is 2:11. The ratio of the number of cookbooks to
the number of reference books is 3: 4. What is the ratio of the number of cookbooks
to the number of novels to the number of reference books at the bookstore?
Answers
Step-by-step explanation:
cookbooks : novels 2 : 11 So 6 : 33 cookbooks : reference books 3 : 4 So 6 : 8
novels : cookbooks : reference books
33 : 6 : 8Answer:
6 : 33 : 8
Step-by-step explanation:
cookbook = C
novel = N
reference book = R
C : N = 2 : 11
C : R = 3 : 4
C : N : R = ?
Start with C : N = 2 : 11
2 is not divisible by 2, so multiply this ratio by 3.
C : N = 6 : 33
C : R = 3 : 4 multiply by 2 to get
C : R = 6 : 8
C : N : R = 6 : 33 : 8
I need the answer ASAP

Answers
Answer:
\(p\leq 56\)
Step-by-step explanation:
Plz mark brainliest!
Enlarge the figure given below by a scale factor of 2.5. Find the perimeter of the new scaled copy.

Answers
The perimeter of the new scaled copy of the figure is:
40 feet + 20.5 feet = 60.5 feet
What do you mean by perimeter?Perimeter is the total length of the boundary or the sum of all the sides of a two-dimensional shape, such as a polygon or a circle.
To enlarge the figure given below by a scale factor of 2.5, we need to multiply all the dimensions of the figure by 2.5.
4 feet x 2.5 = 10 feet
Therefore, the new side length of the square base is 10 feet.
The height of the triangle is 3 feet, and the hypotenuse is 5 feet. To find the length of the base, we can use Pythagorean theorem:
a² + b² = c²
3² + b² = 5²
9 + b² = 25
b² = 16
b = 4
To scale the triangle by a factor of 2.5, we need to multiply both the height and the base by 2.5:
3 feet x 2.5 = 7.5 feet
4 feet x 2.5 = 10 feet
The square base has four sides, each of length 10 feet, so its perimeter is:
4 x 10 feet = 40 feet
We need to add up all three sides to find the perimeter,
10 feet + 7.5 feet + 3 feet = 20.5 feet
To know more about Pythagorean theorem visit:
brainly.com/question/14930619
#SPJ1
pls help pls pls help
Solve the problem below and explain your process.
If the area of a rectangle is (15x2 - 16x - 15) square feet, and its length is (3x - 5) feet,find its width.
Answers
Answer:
Step-by-step explanation:
x^2 + 8x +15 is the area
x+5 is the length
x+3 is the width
(x+5)(x+3)=
x^2 + 3x +5x +15
x^2 +8x + 15