Answers
Related Questions
consider the functions f(x)=x^2 and g(x) = sqrt(x) (a) use linear approximation to approximate the value of f(3.01)
Answers
Using linear approximation, the value of f(3.01) can be approximated by evaluating the tangent line to the function f(x) = x^2 at x = 3 and using it to estimate the value at x = 3.01.
Linear approximation is a method used to estimate the value of a function near a specific point by considering the tangent line at that point. The tangent line is a linear function that approximates the behavior of the original function in the vicinity of the point.
To approximate f(3.01) using linear approximation, we start by finding the slope of the tangent line at x = 3. This can be done by taking the derivative of f(x) = x^2, which is f'(x) = 2x. Evaluating f'(3) gives us the slope of the tangent line at x = 3.
Next, we use the point-slope form of a linear equation to write the equation of the tangent line. Plugging in the values x = 3, y = f(3) = 9, and the slope from f'(3), we can determine the equation of the tangent line.
Finally, we evaluate the tangent line at x = 3.01 to approximate the value of f(3.01). This can be done by substituting x = 3.01 into the equation of the tangent line and solving for y. The resulting value is an approximation of f(3.01) using linear approximation.
To know more about linear approximation click here: brainly.com/question/30403460
#SPJ11
Let $A=\int_a^b f(x) \mathrm{d} x$. Recall that the value of A may be approximated by the Trapezoidal rule on $n$ intervals of width $h=\frac{(b-a)}{n}$ using the formula
$$
T_n=\frac{h}{2} \cdot(f(a)+2 \cdot f(a+h)+2 \cdot f(a+2 \cdot h)+\ldots+2 \cdot f(a+(n-1) \cdot h)+f(b))
$$
For $f(x)=x^2 \cdot \sin (2 \cdot x)$ and $a=0, b=1$, calculate $A$ using Maple to 10 decimal places by using Maple's integration command. Now using a Maple loop, calculate $T_8, T_{16}$ and $T_{32}$ using 10 digit _arithmetic (the default).
Answers
This code will calculate $T_8$, $T_{16}$, and $T_{32}$ using the Trapezoidal rule with 10-digit arithmetic. The `evalf[10]` function is used to obtain the results with 10 decimal places.
To calculate the definite integral $A=\int_a^b f(x) \, dx$ with $f(x)=x^2 \sin(2x)$, $a=0$, and $b=1$, we can use Maple's integration command. Here's the Maple code to calculate the value of $A$:
```maple
f := x -> x^2*sin(2*x);
A := Int(f(x), x = 0 .. 1, 'method' = 'quad');
```
Running this code will give us the value of $A$ to 10 decimal places using Maple's integration command.
To calculate $T_n$ using the Trapezoidal rule with different values of $n$ and 10-digit arithmetic, we can use a Maple loop. Here's the Maple code to calculate $T_8$, $T_{16}$, and $T_{32}$:
```maple
a := 0;
b := 1;
n_values := [8, 16, 32];
for n in n_values do
h := (b - a) / n;
T := 1/2 * h * (f(a) + 2 * add(f(a + i * h), i = 1 .. n-1) + f(b));
evalf[10](T);
end;
```
Running this code will calculate $T_8$, $T_{16}$, and $T_{32}$ using the Trapezoidal rule with 10-digit arithmetic. The `evalf[10]` function is used to obtain the results with 10 decimal places.
Please note that you need to have Maple installed and properly set up to run these commands.
Learn more about arithmetic here
https://brainly.com/question/7882626
#SPJ11
Bill weighs 120 lb and is gaining 10 pounds per month. Phil weighs 204 pounds and is losing 4 pounds per month.
How much will Bill and Phil weigh when they weigh the same amount? Answer (write the number only)
Answers
Answer:
180 pounds
Step-by-step explanation:
In six months Bill's weight will be increased by 60 pounds
10 pounds*6 months=60 pounds
120+60=180
In six months Phil will lose 24 pounds decreasing his weight from 204 to 180
4 pounds*6 months=24 pounds
204-24=180
Answer:
180 lbs
Step-by-step explanation:
204-24= 180
120+60=180
multiply each by 6
What is m
Round the answer to the nearest whole number.
O 30°
O 35°
O 55°
O 60°
Answers
Answer:
30
Step-by-step explanation:
fufyfuf7fjcjcufuy7fufucyyxyvkbuvufudydy shut up
PLEASE HELPPP MEE.....

Answers
Answer:
C ⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀
what's the value of k and p?
\(y = - 5.797 \\ x = 4.0 \\ \frac{k}{y} = \frac{p}{x} + 1\)
Answers
Answer:
We know that:
y = -5.797
x = 4.0
and:
k/y = p/x + 1
We can rewrite this as:
k = (p/x + 1)*y = p*(y/x) + y
Replacing the values of x and y, we get:
k = p*(-5.797/4.0) + (-5.797)
We could simplify this to get:
k = p*(-1.44925) - 5.797
So we ended with a linear equation, so for a given value of p, we know the k.
Now, we could solve this if we add the restriction that k and p must be integers.
Then we can return to:
k = (p/x + 1)*y = (p + x)*(y/x)
replacing the values we get:
k = (p + 4.0)*(-5.797/4.0)
if p = 3996, then p + 4 = 4000
and 4000*(-5.797/4.0) = 1000*(-5.797) = -5797
Then if we take p = 3996, k will also be an integer:
k = (3996 + 4.0)*(-5.797/4.0) = -5797
Then:
p = 3996
k = -5797
is a possible solution of the problem.
Simplify x + 3x – 36.
3x – 36
3x2 – 36
4x – 36
4x2 – 36
Answers
Answer:
4x - 36
Step-by-step explanation:
All we do in this equation is combine the like terms x and 3x and get 4x - 36 :)
Write a number so that the equation will have an infinate number of solutions
3x+5=3x+
Answers
Answer:
3x+5=3x+5
they are both the same line
Answer:
3x+5=3x+5
It is same line
Step-by-step explanation:
2sin^2x= sin^2x+sinxcosx/cotx
Answers
cot(x) = cos(x) / sin(x)
so
cos(x) / cot(x) = 1 / (1/sin(x)) = sin(x)
Then
sin²(x) + sin(x) cos(x) / cot(x) = sin²(x) + sin²(x) = 2 sin²(x)
which of the following is true about the expected value of perfect information?
a. It is the amount you would pay for any sample study.
b. It is calculated as EMV minus EOL.
c. It is calculated as expected value with perfect information minus maximum EMV.
d. It is the amount charged for marketing research.
Answers
The expected value of perfect information (EVPI) is calculated as EVwPI minus maximum EMV. It quantifies the value of perfect information in decision-making.
The expected value of perfect information (EVPI) is a concept used in decision analysis. It represents the maximum amount of money an individual would pay to have perfect information about an uncertain event before making a decision.
To calculate EVPI, you start with the expected value with perfect information (EVwPI), which is the expected value when you have complete and accurate information about the uncertain event. Then, you subtract the maximum expected monetary value (EMV) from the EVwPI.
The EMV represents the expected monetary value of the decision without any additional information. By subtracting the maximum EMV from the EVwPI, you are essentially measuring the value of the additional information in terms of monetary gain.
To know more about Monetary visit.
https://brainly.com/question/28199887
#SPJ11
How do I solve this.

Answers
Answer:
sec θ
Step-by-step explanation:
cos θ + sin θ tan θ
= cos θ + sin θ (sin θ / cos θ)
= cos θ + (sin²θ)/cos θ
= cos θ + (1 - cos²θ) / cosθ
= cos θ + 1/cos θ - cos²θ/cos θ
= cos θ + 1/cos θ - cos θ
= 1/cos θ
= sec θ
Write a linear equation that represents the area and a linear equation that represents the perimeter of the rectangle.
(3x-3) cm and
6 cm
I need a linear equation for for area and a linear equation for perimeter.
Answers
Answer:
Assuming that (3x - 3) and 6 are the sides of the rectangle,
Area:
A = l × w
y = (3x - 3) × (6)
y = 18x - 18
Perimeter:
P = 2l + 2w
y = 2(3x - 3) + 2(6)
y = 6x - 6 + 12
y = 6x + 6
The required linear equation for the area and perimeter of the rectangle is y = 18[x - 1] and z = 6[x + 1] respectively.
Given that, to determine the linear equation that represents the area and a linear equation that represents the perimeter of the rectangle.
The rectangle is 4 sided geometric shape whose opposites are equal in length and all angles are about 90°.
here,
Length = 3x + 3
Width = 6
Area of the rectangle = y, = length × width
y = [3x - 3 ] × [6]
y = 18x - 18 = 18[x -1]
Perimeter of the rectangle = 2[length + width]
z = 2 [3x - 3 + 6]
z = 2 [3x + 3]
z = 6[x + 1]
Thus, the required linear equation for the area and perimeter of the rectangle is y = 18[x - 1] and z = 6[x + 1] respectively.
Learn more about rectangles here:
brainly.com/question/15019502
#SPJ2
What number is 7% smaller than 96
Answers
Answer:
89.28
Step-by-step explanation:
First lets find 7% of 96
96 x 0.07 = 6.72
then subtract 6.72 from 96
96-6.72=89.28
The requried, a number that is 7% smaller than 96 is approximately 89.28.
To find a number that is 7% smaller than 96, we need to calculate 7% of 96 and then subtract that value from 96.
Calculate 7% of 96.
7% of 96 = (7/100) * 96 = 0.07 * 96 = 6.72
To get a number that is 7% smaller than 96, we need to subtract the value we found in Step 1 from 96. subtract the calculated value from 96.
Number = 96 - 6.72 = 89.28
Therefore, a number that is 7% smaller than 96 is approximately 89.28.
Learn more about numbers here:
https://brainly.com/question/20070294
#SPJ4
Jerry bought baseball cards for $5.25 each, and then sold them for $6.30 each. How much profit, in dollars, did Jerry make for selling each one of the baseball cards?
Answers
Answer: $1.05
Step-by-step explanation:
The profit made will be calculated as the difference between the selling price and the cos price. This will be:
= Selling price - Cost price
= $6.30 - $5.25
= $1.05
Therefore, Jerry will make $1.05 profit on each baseball card that's sold.
Using the table and the assumption stated above, determine which of the following conditions are true in this specific case with respect to (a) price, (b) output, and (c) profits. multiple choice 1 a, d, and h b, f, and h a, e, and g c, f, and i
Answers
Based on the information, we can infer that the correct option is A, since all the conditions are true based on the information in the table.
What conditions are true in real life?To identify the conditions that are true in real life we must take into account each of them and contrast it with the reality of the difference between a monopoly and a competitive system. In this case we can infer that the true conditions compared to reality are:
A. The monopoly generally sets higher prices on products than a competitive system.E. Although the monopoly controls a large part of the economy, production is less to maintain a range of consumption and customer needs.G. In monopoly setting higher prices contributes to higher profits than in the competitive system.Learn more about monopoly in: https://brainly.com/question/33076874
#SPJ1

Find the mean, lower quartile and higher quartile
As well as interquartile range

Answers
The mean is 24.31
The lower quartile is 18.
The Higher quartile is 31.
The interquartile range is 13.
What is a mean?It is the average value of the set given.
It is calculated as:
Mean = Sum of all the values of the set given / Number of values in the set
We have,
From the stem and leaf table, we have,
10, 13, 15, 16, 17, 18, 18, 21, 24, 25, 26, 27, 27, 28, 30, 30, 31, 32, 33, 46, 48, 49
Now,
Mean
= 10 + 13 + 15 + 16 + 17 + 18 + 18 + 21 + 24 + 25 + 26 + 27 + 27 + 28 + 30 + 30 + 31 + 32 + 33 + 46 + 48 / 22
= 535 / 22
= 24.31
Lower quartile
First half = 18
Higher quartile
Upper half = 31
Interquartile range.
= Higher quartile - Lower quartile
= 31 - 18
= 13
Thus,
Mean = 24.31
Lower quartile = 18
Upper quartile = 31
Interquartile range = 13
Learn more about mean here:
https://brainly.com/question/23263573
#SPJ1
Matthew recorded the grade-level and instrument of everyone in the middle school School of Rock below. Seventh Grade Students Instrument# of Students Guitar13 Bass11 Drums5 Keyboard3 Eighth Grade Students Instrument# of Students Guitar9 Bass14 Drums8 Keyboard8 Based on these results, express the probability that a student chosen at random will play the keyboard as a decimal to the nearest hundredth.
Answers
Using it's concept, it is found that the probability that a student chosen at random will play the keyboard is of 0.15.
What is a probability?A probability is given by the number of desired outcomes divided by the number of total outcomes.
In this problem:
There is a total of 13 + 11 + 5 + 3 + 9 + 14 + 8 + 8 = 71 students.Of those, 11 play the keyboard.Hence:
\(p = \frac{11}{71} = 0.15\)
The probability that a student chosen at random will play the keyboard is of 0.15.
You can learn more about the probability concept at https://brainly.com/question/15536019
The sum of the ages of Noi's and Noy's is 26 years. The different between four times Noi's age and two times Noy's age is 28 years. Find the age of Noi and Noy.
WRITE AS AN EQUATION
Answers
Answer:
The age of Noi is 13.333 Years and the age of Noy is 12.67 years
Step-by-step explanation:
The given information are;
The sum of the ages of Noi and Noy = 26 years
Four times Noi's age - Two times Noy's age = 28
Let the age of Noi = X and let the age of Noy = Y
We have;
X + Y = 26 years.................(1)
4X - 2Y = 28 years.............(2)
Divide equation (2) by 2 to get;
(4X - 2Y)/2 = (28 years)/2 which gives;
2X - Y = 14 years.................(3)
Add equation (3) to equation (1), to get;
X + Y + 2X - Y = 26 years + 14 years
3X = 40 years
X = 40/3 = 13.333 Years
From equation (1), X + Y = 26 years, therefore;
Y = 26 - X = 26 - 13.33 = 12.67 years
Therefore, the age of Noi = 13.333 Years and the age of Noy = 12.67 years.
Alex leaves home, travels 5 miles east, and arrives at the library. He leaves the library and travels 3 miles north to a friend's house. This trip can be plotted on the coordinate plane, where home is the point (0,0). Alex wants to find out how far his house is from his friend's house and uses the distance formula. Which other formula can he use?.
Answers
Alex uses the Pythagorean distance method to calculate the distance between his home and his friend's home.
5² (a) + 3² (β). Can use any other formulas
Given
After leaving his house, Alex drives five miles to the east to reach the library. He leaves the library and drives three miles to a friend's home in the north.
Home would be, followed by the library and the homes of your friends.
By the Pythagoras theorem, we now have points a, b, and c.
House a2 plus library b2 equals friend's house c2.
He must utilize this formula to resolve the issue. √5² + 3².
√5² + 3².
Learn more about Pythagorean here
https://brainly.com/question/15190643
#SPJ4
PLS HELP ILL MARK AS BRAINLIEST
Given the triangle below, find the value of x and the perimeter of the triangle.

Answers
-7 = 5x -32
25 = 5x
x = 5
Then replace x with 5 and add up the numbers. Then your done.
Find the pay per hour if you earned $120.67 for 16 hours worked.
$1632.32
$1642.72
$6.42
$7.54
Answers
Answer:
$7.54 is the right answer
Answer:
The answer should be $7.54
Step-by-step explanation:
120.67 ÷ 16 = 7.54
120.67 Being the pay for 16 hours
16 being the number of hours
Which tatement would be the mot important in explaining why 2 3 = 6 9 ? A quare i hown and divided into 9 equal-ized quare of 3 row and 3 column. The firt two column are haded. A. 6 of the 9 ame-ized quare are haded and therefore repreent 2 3. B. 6 of the 9 ame-ized quare are haded and therefore repreent 6 9. C. The haded area repreent both 2 3 and 6 9 of the whole hape. D. 2 of the 3 column are haded and therefore repreent 6 9
Answers
The most appropriate statement is that C. The shaded area represent both 2/3 and 6/9 of the whole shape.
What are Fractions?Fractions are numbers which are of the form a/b where a and b are real numbers. This implies that a parts of a number b.
Given a square.
This square is divided in to 9 equal sized squares, with 3 rows and 3 columns.
Out of the 9 equal sized squares, 6 squares are shaded.
We can write the fraction of shaded squares to total number of squares as 6/9.
In the same way, we have in the question that, 6 squares which are shaded is the squares in the first two columns, where each column has three squares.
So we can say that, out of 3 equal sized columns, two columns are shaded.
Fraction of shaded columns to total columns is 2/3.
So 2/3 = 6/9.
Hence shaded area represent both 2/3 and 6/9 of the whole shape.
Learn more about Fractions here :
https://brainly.com/question/10354322
#SPJ1

Malian bought a laptop with a 10% discount. She also bought a mouse for 13.99 and spent 621.49 before tax. Write an equation to find the original cost of the laptop.
Answers
Answer:
(621.49 x 0.1) + 13.99 = x
Step-by-step explanation:
I hope this helps
Sides of a triangle are in the ratio 12:17:25 and its perimeter is 540 cm. Find its area
Answers
Answer:
102
Step-by-step explanation:
(b•h)/2
(12•17)/2
204/2
i need more answers can u give me more answers?
Answers
Answer:
yeah i can help give you answers so what do you need help with
Step-by-step explanation:
Donna has boxes of doughnuts. Each box contains doughnuts. After eating one doughnut, Donna is able to rearrange the remaining doughnuts into bags so that each bag contains doughnuts, and none are left over. What is the smallest possible value of
Answers
The smallest possible value of doughnuts in each box is 2. The smallest possible value of doughnuts in each box is 2.
In order for Donna to rearrange the remaining doughnuts into bags so that each bag contains the same number of doughnuts and none are left over, the number of doughnuts in each box must be divisible by the number of bags. Since there are no doughnuts left over, this means that the number of doughnuts in each box must be a multiple of the number of bags.
To find the smallest possible value, we need to find the smallest common multiple of the numbers 1, 2, 3, 4, 5, 6, 7, 8, and 9 (since there are 9 possible numbers of bags). The smallest common multiple of these numbers is 2, so the smallest possible value of doughnuts in each box is 2.Therefore, the smallest possible value of doughnuts in each box is 2.
To know more about value visit:
https://brainly.com/question/30145972
#SPJ11
What is the value of x?
(Not multiple choice)
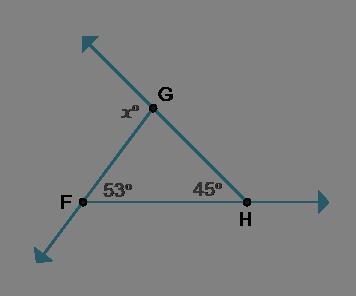
Answers
Answer:
x= 82°
Step-by-step explanation:
According to the angle sum property, sum of all angle in a triangle is 180°
45°+53°+x= 180°
98°+x= 180°
x= 180-98
x= 82°
is 15 square rooted rational
Answers
Answer: The square root of 15 is a rational number
explanation: if 15 is a perfect square. ... Since 15 is not a perfect square, it is an irrational number. This means that the answer to the square root of 15 will have an infinite number of decimals. The decimals will not terminate and you cannot make it into an exact fraction.
Find the value of x. (4x + 12)° 64°

Answers
Answer:
C. 13Step-by-step explanation:
the angle of measure 4x + 12 and the angle of measure 64 are Vertically opposite angles then they are equal in measure
therefore
4x + 12 = 64
⇔ 4x = 64 - 12
⇔ 4x = 52
⇔ x = 52/4
⇔ x = 13
solve for [0,2pi]:cos 2x= 1/2
Answers
We are given the following equation:
\(\cos 2x=\frac{1}{2}\)To solve for "x" we will take arccos to both sides:
\(2x=\text{arccos}(\frac{1}{2})\)Solving the operations:
\(2x=\frac{\pi}{3}\)This is for the first quadrant. Dividing both sides by 2:
\(x=\frac{\pi}{6}\)For the second quadrant we have:
\(2x=\frac{5\pi}{3}\)Dividing both sides by 2:
\(x=\frac{5\pi}{6}\)For the third quadrant we have:
\(2x=\frac{7\pi}{3}\)Dividing by 2:
\(x=\frac{7\pi}{6}\)For the fourth quadrant:
\(2x=\frac{11\pi}{3}\)Dividing by 2:
\(x=\frac{11\pi}{6}\)Therefore, the values of "x" are:
\(x=\frac{\pi}{6},\frac{5\pi}{6},\frac{7\pi}{6},\frac{11\pi}{6}\)