Answers
Answer:
then get un stuck
Step-by-step explanation:
Answer:
y = 2x - 4
Step-by-step explanation:
Slope intercept form: y=mx+b
m=2
point (2,0) means x=2 and y=0
Plug into the equation:
0 = 2(2)+b
0 = 4+b
b = -4
Resulting equation:
y = 2x - 4
Graph:
Start at origin -4 on y-axis. Since slope is 2/1, rise 2 and run 1 to find the line.
Related Questions
A college professor wants to survey a sample of students taking her large lecture course. There are about 150
students in the course, and 10 of those students are graduate students. She wants to take a systematic random
sample of approximately 30 students.
Which of these strategies will accomplish her intended design?
a. randomness select 15 men and 15 women from the class for the survey
b. randomly select 2 graduate students and 28 other students for the survey
c. randomly selects one of the first 5 students to arrive to class, and every 5th student thereafter to take the survey
d. randomly select one of the first 15 students to arrive to class, and every 15th student thereafter to take the survey
e. assign each student a number and use a computer to randomly select 30 students for the survey
Answers
Answer:
B
Step-by-step explanation:
B is the only answer that will ensure she gets graduate students in the sample without getting too few or too many.
Using the concept of systematic sampling, it is found that the correct option is:
c. randomly selects one of the first 5 students to arrive to class, and every 5th student thereafter to take the survey
In a systematic sample, every kth element is chosen.
In this problem, she wants a sample of 30 students, and in total, there are 150 students.
\(\frac{150}{30} = 5\)
Hence, one of the first 5, and then every 5th student should be chosen, and option c is correct.
A similar problem is given at https://brainly.com/question/25122507
Find the slope
Help pls due in one hour

Answers
which of these collections of subsets are partitions of {1, 2, 3, 4, 5, 6}? a) {1, 2}, {2, 3, 4}, {4, 5, 6} b) {1}, {2, 3, 6}, {4}, {5} c) {2, 4, 6}, {1, 3, 5} d) {1, 4, 5}, {2, 6}
Answers
The collections of subsets that are partitions of {1, 2, 3, 4, 5, 6} are options (b) and (c).
Among the given options, collections (b) and (c) are partitions of the set {1, 2, 3, 4, 5, 6}. In option (b), the subsets {1}, {2, 3, 6}, {4}, and {5} form a partition since each element of the set belongs to exactly one subset.
Similarly, in option (c), the subsets {2, 4, 6} and {1, 3, 5} form a partition as each element is assigned to exactly one subset. On the other hand, options (a) and (d) do not satisfy the criteria of being a partition.
A partition of a set is a collection of subsets that satisfies two conditions: The subsets are non-empty. Every element in the original set belongs to exactly one subset in the collection. Let's analyze each option to determine if it is a partition of {1, 2, 3, 4, 5, 6}:
a) {1, 2}, {2, 3, 4}, {4, 5, 6}
This option does not form a partition since the element 2 belongs to both the subsets {1, 2} and {2, 3, 4}. So, option (a) is not a partition.
b) {1}, {2, 3, 6}, {4}, {5}
This option forms a partition. Each element belongs to exactly one subset, and the subsets are non-empty. So, option (b) is a partition.
c) {2, 4, 6}, {1, 3, 5}
This option forms a partition. Each element belongs to exactly one subset, and the subsets are non-empty. So, option (c) is a partition.
d) {1, 4, 5}, {2, 6}
This option does not form a partition since the elements 2 and 6 do not belong to any subset in this collection. So, option (d) is not a partition.
Therefore, the collections of subsets that are partitions of {1, 2, 3, 4, 5, 6} are options (b) and (c).
To know more about subsets click here
brainly.com/question/31739353
#SPJ11
true or false: if a and b are matrices corresponding to orthogonal projections, then the matrix is also the matrix corresponding to some orthogonal projection.
Answers
True , if a and b are matrices corresponding to orthogonal projections, then the matrix is also the matrix corresponding to some orthogonal projection .
Given :
Orthogonal projections of matrices :
A square matrix P is called an orthogonal projector (or projection matrix) if it is both idempotent and symmetric that is, P^2 = P and P′ = P .
The matrix must obey or to be the both symmetric and idempotent matrices to be an orthogonal projector .
so the matrix is also the matrix corresponding to some orthogonal projection .
Learn more about the matrix here:
https://brainly.com/question/28180105
#SPJ4
A spreadsheet ,
a. calculates the interest rate of a new car loan
b. organizes large amounts of information such as a warehouse inventory
c. gives directions to a new location
d. creates a technical drawing
Answers
Jocelyn is going to invest in an account paying an interest rate of 2.3% compounded
continuously. How much would Jocelyn need to invest, to the nearest hundred
dollars, for the value of the account to reach $550 in 15 years?
Answers
9514 1404 393
Answer:
$400
Step-by-step explanation:
The formula for the value of an account with interest rate r compounded continuously for t years is ...
A = Pe^(rt)
We want to find P when A = 550, r = .023, and t = 15.
550 = Pe^(0.023·15) ≈ 1.41199P
P = 550/1.41199 = 389.52 ≈ 400
Jocelyn would need to invest about $400 to reach $550 in 15 years.
Find the volume of the solid formed by rotating the region in the 1st quadrant enclosed by the curves y=x^1/4 and y=x/64 about the y-axis
Answers
The volume of the solid is (3π/5) units^3. To find the volume of the solid formed by rotating the region in the 1st quadrant enclosed by the curves y=x^1/4 and y=x/64 about the y-axis, we can use the method of cylindrical shells.
First, we need to determine the limits of integration. Since the region is in the 1st quadrant, we can integrate from y=0 to y=1. To find the corresponding x-values for these limits, we can set y=x^1/4 and y=x/64 equal to 1 and solve for x:
x^1/4 = 1 => x = 1
x/64 = 1 => x = 64
So, our limits of integration are x=1 to x=64.
Next, we need to find an expression for the radius of each cylindrical shell. The radius is simply the distance from the y-axis to the curve at a given y-value. So, for a given y, the radius is:
r = x - x^1/4
Finally, we need to find an expression for the height of each cylindrical shell. The height is the infinitesimal change in y, which is simply dy. So, the volume of each cylindrical shell is:
dV = 2πr dy
Putting it all together, we have:
V = ∫(2πr) dy from y=0 to y=1
= ∫2π(x - x^1/4) dy from y=0 to y=1
= 2π ∫(x - x^1/4) dy from y=0 to y=1
= 2π ∫(y^4 - y) dy from y=0 to y=1
= 2π [y^5/5 - y^2/2] from y=0 to y=1
= 2π [(1/5) - (1/2)]
= (3π/5) units^3
Therefore, the volume of the solid is (3π/5) units^3.
Learn more about quadrant here:
https://brainly.com/question/26426112
#SPJ11
What is the distance between the following points?

Answers
Answer:
The answer is 6 i believe sorry if i am wrong
Find the value of y for the given value of x.a. y = 10x; x = -3b. y = 6 - 2x; x = 11 c. y = 4x + 5; x = 1/2
Answers
Part a
y = 10x
For x=-3
substitute the value of x in the equation and evaluate it
y=10(-3)=-30
Part b
y = 6 - 2x
For x=11
y=6-2(11)=-16
Part c
y = 4x + 5
For x=1/2
y=4(1/2)+5=7
Brandy needs 2
yards of fabric to make one blanket. If she wants to make four blankets, how much total fabric will she need ?
Answers
Because 2y * 4 strands = 8
Please Help I WILL MARK YOU BRAINLIEST.SHOW YOUR WORK PLEASE

Answers
Answer:
3⅞ is the answer to the question.
Step-by-step explanation:
The ten lightest tomatoes are in ¼, ⅜, ½, ⅝ and ⅞.
In ¼, there are 3 tomatoes, so that would be “¼×3=¾”.
In ⅜, there are 2 tomatoes, so that would be “⅜×2=¾”.
In ½, there are 3 tomatoes, so it would be “½×3=3/2”.
In ⅝, there is 1 tomato, so it would be “⅝×1=⅝”.
In ⅞, there is 1 tomato, so that would be “⅞×1=⅞”.
Now add all together:
¾ + ¾ + 3/2 + ⅝ + ⅞
= 5+5+7+6+8/8
= 31/8
= 3⅞
arrange the given steps in the correct order to prove that 3n6, 3^k 3^k+1 < (k+1)!
3^k+1 < (k+1) * 3^k
For n = 7.3^7 = 2187 < 7! + 5040
3^k=1 < (k+1) * k!
3^k+1 = 3 * 3^k
Answers
The correct order of steps to prove the inequality 3^n < (n+1)! for n = 7 is as follows: 3^k < (k+1) * k!, 3 * 3^k = 3^(k+1), 3^(k+1) < (k+1) * 3^k; For n = 7, 3^7 = 2187: 2187 < 7! + 5040.
To prove the inequality 3^n < (n+1)! for n = 7, we can follow these steps:
Start with the assumption that 3^k < (k+1) * k! is true for some positive integer k.
Multiply both sides of the inequality by 3 to get 3^(k+1) < 3 * (k+1) * k!.
Simplify the right side to obtain 3^(k+1) < (k+1) * (k+1) * k!.
Rewrite (k+1) * (k+1) as (k+1)^2.
By substitution, we have 3^(k+1) < (k+1)^2 * k!.
Now, consider the case where n = 7. We substitute k = 6 in the inequality.
Evaluating both sides of the inequality for n = 7, we find that 3^7 = 2187.
Calculate (7+1)! = 8! = 40320.
Compare the values: 2187 < 40320.
Since 2187 is indeed less than 40320, the inequality holds true for n = 7.
Therefore, we have successfully shown that 3^n < (n+1)! for n = 7.
To know more about inequality,
https://brainly.com/question/24848865
#SPJ11
Find a formula for the polynomial P(x) with - degree 3 - a root of multiplicity 2 at x=4 - a root of multiplicity 1 at x=−5 - y-intercept (0,−48) P(x)=
Answers
The polynomial P(x) can be represented as P(x) = a(x - 4)^2(x + 5), where a is a constant.
Given that P(x) has a degree of 3, a root of multiplicity 2 at x = 4, and a root of multiplicity 1 at x = -5, we can determine the general form of the polynomial. A root of multiplicity 2 at x = 4 indicates that the factor (x - 4) appears twice in the polynomial, and a root of multiplicity 1 at x = -5 indicates that the factor (x + 5) appears once.
Hence, the polynomial can be written as P(x) = a(x - 4)^2(x + 5), where a is a constant that needs to be determined.
To find the value of a, we can use the y-intercept information. The y-intercept is given as (0, -48), which means that when x = 0, P(x) = -48. Substituting these values into the polynomial equation, we have -48 = a(0 - 4)^2(0 + 5).
Simplifying this equation, we get -48 = 100a. Solving for a, we find a = -48/100 = -12/25.
Therefore, the polynomial P(x) is P(x) = (-12/25)(x - 4)^2(x + 5).
learn more about polynomial equation here:
https://brainly.com/question/28947270
#SPJ11
y f(n) = sin nπ/2 then G(n) = 2/π² (Sin nπ/2 - Sin² nπ/2)
Answers
The function G(n) in terms of f(n) is G(n) = 2/π² (f(n) - f²(n)).
To find the function G(n) in terms of f(n) based on the given expression, we substitute f(n) into the formula for G(n):
G(n) = 2/π² (Sin nπ/2 - Sin² nπ/2)
Replacing Sin nπ/2 with f(n), we have:
G(n) = 2/π² (f(n) - Sin² nπ/2)
Since f(n) is defined as f(n) = Sin nπ/2, we can simplify further:
G(n) = 2/π² (Sin nπ/2 - Sin² nπ/2)
Now we can substitute f(n) = Sin nπ/2 into the equation:
G(n) = 2/π² (f(n) - f²(n))
Therefore, the function G(n) in terms of f(n) is G(n) = 2/π² (f(n) - f²(n)).
Learn more about function here:
https://brainly.com/question/11624077
#SPJ11
Joaquin took a quiz worth 45 points. He earned 40 points. What was his score
(percent) in the gradebook?
Answers
Answer:
88.8888888889% or 88% rounded
plz Brainliest?!?!?
a tree is sold based on the circumstances of the tree .if a tree has a radius of 4 inches then what is the circumference of the tree
Answers
Answer:
circumference =2πr
2x22/7x4
44/7x4
=176/7
=25.142857
Use a and b = < 5, 1, -2> Find ||al| (answer1] Find [answer2] Find b-a [answer3] Find a b [answer4] . Find a x b [answer5]
Find the limit lime-T/6 cose, sin30,0
Answers
1) ||a|| = sqrt(30) 3) b - a = <5 - 5, 1 - 1, -2 - (-2)> = <0, 0, 0> 4)a · b = 55 + 11 + (-2)*(-2) = 25 + 1 + 4 = 30 5) a x b = <(1*(-2) - (-2)1), (-25 - 5*(-2)), (51 - 15)> = <0, -20, 0>. lim(T → 6) (cos(e) + sin(30) + 0) = cos(6) + sin(30) + 0
Norm of vector a: The norm (or magnitude) of a vector is found by taking the square root of the sum of the squares of its components. For vector a = <5, 1, -2>, the norm ||a|| is calculated as follows:
||a|| = sqrt(5^2 + 1^2 + (-2)^2) = sqrt(30) = answer1.
Cross product of vectors a and b: The cross product of two vectors is calculated using the determinant of a 3x3 matrix. For vectors a = <5, 1, -2> and b = <5, 1, -2>, the cross product a x b is found as follows:
a x b = <(1*(-2) - (-2)1), (-25 - 5*(-2)), (51 - 15)> = <0, -20, 0> = answer5.
Difference b-a: To find the difference between vectors b and a, we subtract the corresponding components. For vectors a = <5, 1, -2> and b = <5, 1, -2>, we have:
b - a = <5 - 5, 1 - 1, -2 - (-2)> = <0, 0, 0> = answer3.
Dot product of vectors a and b: The dot product of two vectors is found by multiplying the corresponding components and summing the results. For vectors a = <5, 1, -2> and b = <5, 1, -2>, we have:
a · b = 55 + 11 + (-2)*(-2) = 25 + 1 + 4 = 30 = answer4.
Limit evaluation: To find the limit of the given expression, we substitute the given value into the trigonometric functions:
lim(T → 6) (cos(e) + sin(30) + 0) = cos(6) + sin(30) + 0 = answer5.
To learn more about vectors click here, brainly.com/question/24256726
#SPJ11
Which graph solves the following system? x+2y=4 5x−2y=8

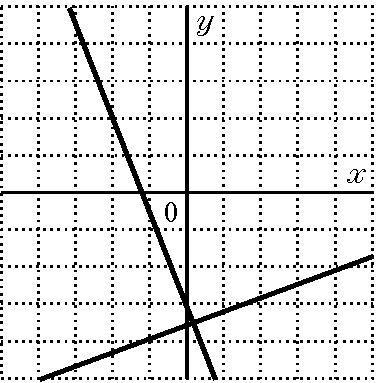


Answers
Answer:
elimination method
x+2y=4 1
5x-2y=8 2
1+2
6x=12
x=2
plug into x+2y=4
2+2y=4
2y=4-2
2y=2
y=1
(2,1)
so graph 1
the height of a projectile at time t is represented by the function h (t)= −4.9 t2 18 t 40 .
Answers
The maximum height of the projectile is 56.53 meters.
The height of a projectile at time t is represented by the function h (t)= −4.9 t² +18t + 40, where h(t) is the height in meters and t is the time in seconds.
This is a quadratic function of the form h(t) = at² + bt + c, where a = -4.9, b = 18, and c = 40.
To find the maximum height of the projectile, we need to find the vertex of the parabolic graph of the function h(t).
The vertex of the parabola is at the point (t, h(t)) where t = -b/2a. Substituting the values of a and b, we get t = -18/(2(-4.9)) = 1.8367 seconds.
To find the maximum height, we need to substitute t = 1.8367 seconds into the function h(t). h(1.8367) = -4.9(1.8367)^2 + 18(1.8367) + 40 = 56.53 meters.
To learn more about the quadratic function;
https://brainly.com/question/11485644
#SPJ1
Assume that sin(x) equals its Maclaurin series for all x. Use the Maclaurin series for sin (8x²) to evaluate the integral 0.78 [** sin(8x²) da Your answer will be an infinite series. Use the first two terms to estimate its value.
Answers
To evaluate the integral ∫[0, 0.78] sin(8x²) dx using the Maclaurin series for sin(8x²), we can substitute the Maclaurin series into the integral. The Maclaurin series for sin(8x²) is given by:
sin(8x²) = 8x² - (8x²)³/3! + (8x²)⁵/5! - (8x²)⁷/7! + ...
Substituting this series into the integral, we have:
∫[0, 0.78] (8x² - (8x²)³/3! + (8x²)⁵/5! - (8x²)⁷/7! + ...) dx
Integrating each term separately, we get:
∫[0, 0.78] 8x² dx - ∫[0, 0.78] (8x²)³/3! dx + ∫[0, 0.78] (8x²)⁵/5! dx - ∫[0, 0.78] (8x²)⁷/7! dx + ...
Evaluating each integral term, we have:
(8/3)x³ - (8/3!)(8/3)²x⁵ + (8/5!)(8/5)²x⁷ - (8/7!)(8/7)²x⁹ + ...
To estimate the value of the integral, we can use the first two terms of the series. Plugging in the values, we have:
(8/3)(0.78)³ - (8/3!)(8/3)²(0.78)⁵ ≈ 1.564
Therefore, using the first two terms of the series, the estimated value of the integral ∫[0, 0.78] sin(8x²) dx is approximately 1.564.
Learn more about series here:
brainly.com/question/30457228
#SPJ11
A textbook is opened at random. What page numbers is the book opened to if the product of the opened page numbers is 132?
Answers
The book is opened to pages 11 and 12.
How to get the product of the page
So, we can write the equation:x * (x + 1) = 132
Expanding the equation, we get:
x² + x = 132
To solve for x, we need to rewrite the equation as a quadratic equation:
x²+ x - 132 = 0
Now, we can factor the quadratic equation:
(x - 11)(x + 12) = 0
This equation has two solutions for x:
x = 11
x = -12
Since page numbers cannot be negative, we discard the second solution. Thus, the left-hand page number is 11, and the right-hand page number is 11 + 1 = 12.
So, the book is opened to pages 11 and 12.
Read more on product of numbers here : https://brainly.com/question/25301924
#SPJ1
Evaluate yz + x² x=3.2, y=6.1, z=0.2
Answers
Answer:
Step-by-step explanation:
To evaluate the given expression, we need to substitute the given values for x, y, and z. The expression becomes:
yz + x²
Substituting the given values, we get:
(6.1 * 0.2) + (3.2^2)
This simplifies to:
1.22 + 10.24
Therefore, the value of the expression is approximately 11.46.
11.46
gimme brainlyest gang
Official guidelines that govern what the group is supposed to do and how members are supposed to behave are called?
Answers
Official guidelines that govern what the group is supposed to do and how members are supposed to behave are called "bylaws" or "rules and regulations."
Official guidelines, such as bylaws or rules and regulations, serve as a framework that outlines the purpose, structure, and functioning of a group or organization. These guidelines provide clarity on the group's objectives, the roles and responsibilities of its members, decision-making processes, and expected behaviors.
Bylaws typically cover various aspects, including membership requirements, meeting procedures, voting procedures, officer positions and duties, financial management, dispute resolution mechanisms, and any other relevant policies. They serve as a reference point for members to understand their rights, obligations, and the overall functioning of the group.
These guidelines help ensure consistency, fairness, and accountability within the group. They establish a common set of expectations and provide a structure for decision-making and problem-solving. Bylaws also help maintain order and facilitate effective collaboration among group members.
In summary, official guidelines, such as bylaws or rules and regulations, are essential for providing a clear framework and establishing standards for the functioning and behavior of a group or organization. They contribute to the group's cohesion, effectiveness, and the achievement of its objectives.
Learn more Official guidelines: https://brainly.com/question/14523060
#SPJ11
Given the following three points, find by hand the quadratic function they represent.
(-1,-8), (0, -1),(1,2)
(1 point)
O f() = -5x2 + 8x - 1
Of(x) = -222 +50 - 1
O f(x) = -3.x2 + 4.0 – 1
O f() = -3x2 + 10x - 1
Answers
Answer:
The equation is;
f(x) = -2·x² + 5·x - 1
Step-by-step explanation:
The general form of a quadratic equation or function f(x) is, f(x) = y = a·x² + b·x + c
Given that the points representing the quadratic function are;
(-1, -8), (0, -1), (1, 2) which are of the form (x, y)
When x = -1, f(x) = y = -8
Plugging in the above values into the general form of a quadratic function, we have;
-8 = a·(-1)² + b·(-1) + c = a - b + c
-8 = a - b + c.........................(1)
When x = 0, y = -1, we have;
-1 = a·(0)² + b·(0) + c = c
c = -1.......................................(2)
When x = 1, y = 2, which gives;
2 = a·(1)² + b·(1) + c = a + b + c
2 = a + b + c........................(3)
Adding equation (1) to equation (3), we have;
-8 + 2 = a - b + c + a + b + c
-8 + 2 = 2·a + 2·c
From equation (2) c = -1, we get;
-8 + 2 = -6 = 2·a + 2·c = 2·a + 2 × (-1)
-6 = 2·a - 2
-4 = 2·a
a = -2
From equation (3), we have
2 = a + b + c
Substituting the values of a, and c gives;
2 = -2 + b - 1
b = 2 + 2 + 1 = 5
b = 5
The equation is therefore;
f(x) = -2·x² + 5·x - 1.
Answer:
b
Step-by-step explanation:
48 divided by 2+6 x2-1
Answers
Answer: 35
Step-by-step explanation:
Write the ratio of corresponding sides for the similar triangles and reduce the ratio to lowest terms.
a.
10
d.
4 5
b. 4 5
I
s 100
10
4
8
--
8 10
415
이
00
I
C. 10 85
815
I
10
I
2/5
I
211
552
415
Mark this and return
Next
Submit
Answers
The ratio of corresponding sides for the given similar triangles is 2/5.
In the given options, the ratio of corresponding sides is provided for each set of similar triangles. Let's analyze each option to determine the correct ratio:
a. 10
This option only provides a single number and does not specify the ratio of corresponding sides. Therefore, it is not the correct answer.
b. 4/5
This option provides the ratio 4/5 for the corresponding sides of the similar triangles. However, the ratio can be simplified further.
To simplify the ratio, we divide both the numerator and denominator by their greatest common divisor (GCD). In this case, the GCD of 4 and 5 is 1.
Dividing 4 and 5 by 1, we get:
4 ÷ 1 = 4
5 ÷ 1 = 5
Therefore, the simplified ratio is 4/5.
c. 10/85
This option provides the ratio 10/85 for the corresponding sides of the similar triangles. However, this ratio cannot be simplified further, as 10 and 85 do not have a common factor other than 1.
Therefore, the correct ratio of corresponding sides for the given similar triangles is 2/5, as determined in option b.
For more such questions on triangles, click on:
https://brainly.com/question/17335144
#SPJ8
Please help me answer the question

Answers
Answer:
\(\frac{4k}{3}+5=18\)
Step-by-step explanation:
→ Start of with k being divided by 3
\(\frac{k}{3}\)
→ Multiplied by 4
\(\frac{k}{3}*4=\frac{4k}{3}\)
→ Added to 5
\(\frac{4k}{3}+5\)
→ The answer is 18
\(\frac{4k}{3}+5=18\)
7. y = 5x
8. k/3 × 4 + 5 = 18
9. y = 2x + 120
--------------
Explanations:if the price of car is xif the price of house is y
so y=5x
based on the given conditions, formulatek/\(3x\(4+\(5=18
assume: x for chairy for table
according to the problem
y=2x+120
If the answer is right for my question you get brainilest!!!

Answers
Answer:hello
Step-by-step explanation:
The weight of one serving of trail mix is 2.5 ounces. How many servings are there in 25 ounces of trail mix?
Answers
Explanation: 25/2.5 = 10
−3−(−5) what is the answer to this problem ive tried everything
Answers
Answer: 2
Step-by-step explanation:
