Answers
Answer:
Look below.
Step-by-step explanation:
13.)
The lines are neither because the slopes are reciprocals.
14.)
The lines are perpendicular because the slopes are opposite reciprocals.
Related Questions
Consider the following time series model for {y} Y₁ = Yı−1+€₁+AEL-11 where E, is i.i.d with mean zero and variance o², for t = 1,..., 7. Let yo = 0. Demon- strate that y, is non-stationary unless \-1. In your answer, clearly provide the conditions for a covariance stationary process. Hint: Apply recursive substitution to express y, in terms of current and lagged errors. (b) (3 marks) Briefly discuss the problem of applying the Dickey Fuller test when testing for a unit root when the model of a time series is given by: I₁ = pri-1 + 14. where the error term , exhibits autocorrelation. Clearly state what the null, alternative hypothesis, and the test statistics are for your test.
Answers
The null and alternative hypotheses of the test are Null Hypothesis: The series has a unit root (non-stationary)Alternative Hypothesis: The series does not have a unit root (stationary)The test statistic for the ADF test is similar to that of the Dickey-Fuller test.
(a)Consider the following time series model: {y} Y₁ = Yı−1+€₁+AEL-11 where E, is i.i.d with mean zero and variance o², for t = 1,..., 7.
Let yo = 0We need to demonstrate that y, is non-stationary unless \-1.
To do that, we shall apply recursive substitution to express yt in terms of current and lagged errors.
y1= y0+ε1+AE1-1
= 0 + ε1 + AE1-1
= ε1 + AE1-1, which is the initial observation
y2= y1+ε2+AE1
= ε1 + AE1-1+ε2 + AE2-1
= ε1+ ε2+ AE1-1+ AE2-1
= ε1+ ε2+ A(ε1+AE1-2)
= (1+A)ε1+ ε2+ A²E1-2....
It can be shown by induction that yt = εt + Aεt-1+ A²εt-2+…+ At-1ε1+Aty0
=0yt
= εt+ Ayt-1
Now, y_t depends on y_t-1 and ε_t. So, the model is not covariance stationary, unless the |A| < 1 .
Conditions for a covariance stationary process: For a time series to be covariance stationary, the following conditions must be met:1.
Mean function of the series should exist and should be constant over time.2. Variance function of the series should exist and should be constant over time.3.
The covariance between any two observations should depend only on the lag between them and not on the time at which the covariance is computed.
(b) The problem of applying the Dickey-Fuller test when testing for a unit root when the model of a time series is given by: I₁ = pri-1 + 14 where the error term exhibits autocorrelation arises because in this case, the error terms are not independent and identically distributed (i.i.d.).
Therefore, the distributional properties of the Dickey-Fuller test are violated, making it inappropriate to use.
To test for a unit root in this case, the Augmented Dickey-Fuller (ADF) test should be used instead.
The null and alternative hypotheses of the test are: Null Hypothesis: The series has a unit root (non-stationary)Alternative Hypothesis:
The series does not have a unit root (stationary)The test statistic for the ADF test is similar to that of the Dickey-Fuller test.
Know more about Null Hypothesis here:
https://brainly.com/question/4436370
#SPJ11
a runner ran 2/3 of 5 km race in 21 minutes how long does it take to run the entire race
Answers
Answer:
31.5 min
Step-by-step explanation:
you divide 21 in hald to get 10.5 which is 1/3 to multiply by 3 for a whole race getting 31.5
I need the function for the volume of the box for number 1

Answers
Answer:
Step-by-step explanation:
v = l * w * h
v = x * 22 * 28
v = 616x
the nth term of a quadratic sequence can be written as an^2 + bn +c. Here are its first 4 terms. 3, 14, 29, 48. find the values of a, b and c.
Answers
The values of a , b and c in the given quadratic sequence are
a = 2, b = 5, c = -4
Quadratic Sequence:The ordered collections of numbers known as quadratic sequences are based on the rule n2 = 1, 4, 9, 16, 25. (the square numbers). Every quadratic sequence has a n2 term.
Now in the given question ,
For nth term we have,
an² + bn + c
n = 1:
a + b + c = 3 Eq. 1
n = 2:
4a + 2b + c = 14 Eq. 2
n = 3:
9a + 3b + c = 29 Eq. 3
Eq. 2 minus Eq. 1
3a + b = 11 Eq. 4
Eq. 3 minus Eq. 2
5a + b = 15 Eq. 5
Eq. 5 minus Eq. 4
2a = 4
a = 2
Plug in a = 2 into Eq. 4
3(2) + b = 11
b = 5
Plug in a = 2 and b = 5 into Eq. 1.
2+5 + c = 3
c = -4
The required values are , a = 2, b = 5, c = -4.
learn more about quadratic sequence , visit:
https://brainly.com/question/22412845
#SPJ1
Rearrange x + 2y = 9 to the form y=mx+c
Answers
Answer:
2y=9-x
y=9-x/2
9/2-x/2=mx+c
c=9/2
m=-1/2
Answer:
the answer of this question is
2y=-x+9
What is the Gini Co-efficient? What does it measure and mean? Wh. has been happening to this measure in the U.S over the last 50 years? 2. What is the number of the Gini Co-efficient when a country is 100% equal? Why? 3. What is the number of the Gini co-efficient when a country is completely unequal? (one person in a country has ALL the income.) 4. Give and explain one definition of a market. 5. Give and explain one reason why markets fail.
Answers
The Gini coefficient is a statistical measure of income inequality, ranging from 0 to 1. It measures the dispersion of income within a population.
Over the past 50 years in the United States, there has been a significant increase in income inequality, with the Gini coefficient steadily rising. Factors such as technological advancements, globalization, stagnant wages, and policy changes have contributed to this trend.
A country with perfect income equality would have a Gini coefficient of 0, indicating that all individuals have the same income. Conversely, a country with complete income inequality, where one person possesses all the income, would have a Gini coefficient of 1, representing maximum inequality.
A market is a system facilitating the exchange of goods, services, or resources between buyers and sellers. It enables supply and demand to interact, allowing negotiations on price, quantity, and terms. However, markets can fail due to externalities, which are the positive or negative impacts of production or consumption on third parties.
When externalities exist, the market may not consider the total costs or benefits associated with a product or service. For example, if a factory pollutes the environment, the market price may not include the costs of pollution. This can lead to overproduction, inefficient resource allocation, and negative social consequences. To address market failures caused by externalities, governments may intervene with regulations, taxes, or subsidies to ensure more socially desirable outcomes.
Learn more about inequality here:
https://brainly.com/question/25944814
#SPJ11
A random sample of size 36 is taken from a normal population with a mean of 50 and a standard deviation of 5. What is the sample standard deviation?
Answers
The sample standard deviation is approximately 0.83.
Sample size \(($n$)\) = 36
Population mean \(($\mu$)\) = 50
Population standard deviation \(($\sigma$)\) = 5
The sample standard deviation, denoted as \($s$\) can be estimated using the formula:
\(\[ s = \sqrt{\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n-1}} \]\)
where:
\($x_i$\) represents the individual data points in the sample
\($\bar{x}$\) is the sample mean
In this case, since we don't have individual data points, we can use the population standard deviation as an estimate for the sample standard deviation when the sample size is relatively large (as in this case \($n = 36$\)). This approximation is known as the standard error of the mean.
Therefore, the sample standard deviation can be approximated as:
\(\[ s \approx \frac{\sigma}{\sqrt{n}} \]\)
Substituting the given values:
\(\[ s \approx \frac{5}{\sqrt{36}} = \frac{5}{6} \] = 0.83\)
Hence, the sample standard deviation is approximately 0.83.
Learn more about sample standard deviation: https://brainly.com/question/18567452
#SPJ11
Questions 21 - 25 relate to the following information. Suppose a firm's total cost curve is \( c=100+2 q \), where \( c \) is total cost and \( q \) is quantity of units. What is the yaxis intercept?
Answers
The y-axis intercept of the total cost curve is 100.
The y-axis intercept represents the value of the dependent variable when the independent variable is zero. In this case, the y-axis intercept represents the total cost when the quantity of units is zero.
Given the total cost curve c = 100 + 2q, we can find the y-axis intercept by setting q to zero:
c = 100 + 2(0)
c = 100
Therefore, the y-axis intercept of the total cost curve is 100.
To know more about y-axis intercept , refer here:
https://brainly.com/question/12716308
#SPJ4
Observation, experimentation, and mathematics, in combination, produce reliable results. This statement describes a development of thought during which period?.
Answers
This statement describes a period known as the Scientific Revolution.
The Scientific Revolution: What Was It?
The 16th and 17th centuries saw a radical shift in scientific ideas that is known as the Scientific Revolution.
During the Scientific Revolution, a new understanding of nature replaced the Greek perspective that had dominated science for nearly two thousand years.
The Scientific Revolution was absent?
The Enlightenment, an intellectual and social movement, was influenced by the scientific revolution, which started in Europe at the end of the Renaissance and lasted until the late 18th century.
Learn more about Scientific Revolution
brainly.com/question/14328830
#SPJ4
Brigid is picking strawberries at the Pick-Your-Own Farm. Her goal is to pick 5 bushels of strawberries. She has already picked 1
1
2
bushels, and she picks at a rate of
5
8
bushel per hour. The scenario is represented as
5
8
h + 1
1
2
= 5, where h is the number of hours she picks. How many more hours will it take Brigid to fill 5 bushels of strawberries?
2 and StartFraction 3 Over 16 EndFraction hours
2 and StartFraction 3 Over 16 EndFraction hours
5 and three-fifths hours
10 and two-fifths hours
Answers
Answer:
We can start by isolating the variable "h".
5 8 h + 1 1 2 = 5
Subtracting 11/2 from both sides:
5 8 h = 5 - 1 1 2
Simplifying:
5 8 h = 8 1 2
Dividing both sides by 5/8:
h = 8 1 2 ÷ 5 8
Converting the mixed number to an improper fraction:
h = (8 x 8 + 1) ÷ 5 8
h = 65/8
Now, we can convert this fraction to a mixed number:
h = 8 1/8
Brigid has already picked for 8 1/8 hours, so the amount of time needed to pick the remaining strawberries is:
5 - (1 1/2 + 5/8 x 8) = 5 - (3 5/8) = 1 3/8
Therefore, Brigid still needs to pick for 1 3/8 hours to fill 5 bushels of strawberries. The answer is 1 and 3/8 hours or 2 and 3/16 hours (if simplified).
Step-by-step explanation:
what is the surface area of a cylider using 3.14 with a radius 15 and hight of 72
Answers
The surface area of a cylinder using 3.14 with a radius 15 and hight of 72 is 8195.4 square unit.
Given that
Radius of cylinder = 15
Height of cylinder = 72
We have calculate the surface area of cylinder
Since we know that
A cylinder's surface area is the area occupied by its surface in three dimensions.
A cylinder is a three-dimensional structure with circular bases that are parallel. It is devoid of vertices. In most cases, the area of three-dimensional shapes refers to the surface area.
Surface area is measured in square units. For instance, cm², m², and so on.
A cylinder is made up of circular discs that are placed on top of one another. Because the cylinder is a three-dimensional solid, it contains both surface area and volume.
Surface area of cylinder = 2πrh + 2πr²
Here r represents radius of cylinder
And h represents height of cylinder
Now put the values we get
= 2x3.14x15x72 + 2x3.14x15x15
= 6782.4 + 1413
= 8195.4
Hence the surface area of the given cylinder = 8195.4
square unit.
To learn more about surface area of cylinder visit:
https://brainly.com/question/27803865
#SPJ1
PLEASE SOMEONE ANSWER

Answers
I would say -2
Step-by-step explanation:
(a) Find the values of z, zER, for which the matrix
x3 x
9 1
has inverse (marks-2 per part)
x=
x=
x=
(b) Consider the vectors - (3,0) and 7- (5,5).
(i.) Find the size of the acute angle between i and ü. Angle-
(ii). If -(k, 3) is orthogonal to , what is the value of ke k [2 marks]
(c) Let J be the linear transformation from R2 R2 which is a reflection in the horizontal axis followed by a scaling by the factor 2.
(i) If the matrix of J is W y 1₁ what are y and z
y= [2 marks]
z= [2 marks] U N || 62 -H 9 has no inverse. [6 marks-2 per part] [2 marks]
(d) Consider the parallelepiped P in R³ whose adjacent sides are (0,3,0), (3, 0, 0) and (-1,1, k), where k € Z. If the volume of P is 180, find the two possible values of k. [4 marks-2 each]
k=
k=
(e) Given that the vectors = (1,-1,1,-1, 1) and =(-1, k, 1, k, 8) are orthogonal, find the magnitude of . Give your answer in surd form. [3 marks]
v=
Answers
(a) To find the values of z for which the matrix does not have an inverse, we can set up the determinant of the matrix and solve for z when the determinant is equal to zero.
The given matrix is:
|x3 x|
|9 1|
The determinant of a 2x2 matrix can be found using the formula ad - bc. Applying this formula to the given matrix, we have:
Det = (x3)(1) - (9)(x) = x3 - 9x
For the matrix to have an inverse, the determinant must be non-zero. Therefore, we solve the equation x3 - 9x = 0:
x(x2 - 9) = 0
This equation has two solutions: x = 0 and x2 - 9 = 0. Solving x2 - 9 = 0, we find x = ±3.
So, the values of x for which the matrix has no inverse are x = 0 and x = ±3.
(b) (i) To find the size of the acute angle between the vectors (3,0) and (5,5), we can use the dot product formula:
u · v = |u| |v| cos θ
where u and v are the given vectors, |u| and |v| are their magnitudes, and θ is the angle between them.
Calculating the dot product:
(3,0) · (5,5) = 3(5) + 0(5) = 15
The magnitudes of the vectors are:
|u| = sqrt(3^2 + 0^2) = 3
|v| = sqrt(5^2 + 5^2) = 5 sqrt(2)
Substituting these values into the dot product formula:
15 = 3(5 sqrt(2)) cos θ
Simplifying:
cos θ = 15 / (3(5 sqrt(2))) = 1 / (sqrt(2))
To find the acute angle θ, we take the inverse cosine of 1 / (sqrt(2)):
θ = arccos(1 / (sqrt(2)))
(ii) If the vector (-k, 3) is orthogonal to (5,5), it means their dot product is zero:
(-k, 3) · (5,5) = (-k)(5) + 3(5) = -5k + 15 = 0
Solving for k:
-5k = -15
k = 3
So, the value of k is 3.
(c) Let J be the linear transformation from R2 to R2 that reflects points in the horizontal axis and then scales them by a factor of 2. The matrix of J can be found by multiplying the reflection matrix and the scaling matrix.
The reflection matrix in the horizontal axis is:
|1 0|
|0 -1|
The scaling matrix by a factor of 2 is:
|2 0|
|0 2|
Multiplying these two matrices:
J = |1 0| * |2 0| = |2 0|
|0 -1| |0 2| |0 -2|
So, the matrix of J is:
|2 0|
|0 -2|
Therefore, y = 2 and z = -2.
(d) The volume of a parallelepiped can be found by taking the dot product of two adjacent sides and then taking the absolute value of the result.
The adjacent sides of the parallelepiped P are (0,3,0)
To learn more about scaling matrix click here : brainly.com/question/16662440
#SPJ11
I used 15 out of the 48 rolls of toilet paper that I bought. What percent did I use so
far? Round to the nearest tenths place and include the percent sign.
Answers
Answer:
Step-by-step explanation:
15 rolls................................? %
48 rolls................................100%
(15*100)/48=31.25% used
round to the nearest tenth is 31.30%
Can anyone help me with this?

Answers
Answer:
B.16 mins start from home to school or school to home
Step-by-step explanation:
I. When bike is faster than walk 3 times
Jane is in the middle of way to school
if she walk mid point to school is 4 mins
then mid point to home is 4 * 3 = 12 mins
School + Home = Total Mins
4 + 12 = 16
More discuss, leave comment below.
Twice the difference of a number and 4 to is 5
Answers
Thus, the value of the unknown number for the given word problem is found as :x = 6.5.
Explain about the word problems:A word problem is an exercise in mathematics that takes the form of such a hypothetical query and requires the solution of equations and mathematical analysis.
Using the "GRASS" method to solve word problems is a solid strategy. Given, Required, Analytic, Solution, and Statement is also known as GRASS. A word issue can be simplified using GRASS, making it simpler to solve.
Given word problems:
Twice the difference of a number and 4 is 5
Let the unknown number be 'x'.
Now,
The difference of the number and 4 : x - 4
Twice the result : 2(x - 4)
The outcome equals the 5.
2(x - 4) = 5 (Requires equation)
Solve the expression to find the number:
2(x - 4) = 5
2x - 8 = 5
2x = 5 + 8
2x = 13
x = 13/2
x = 6.5
Thus, the value of the unknown number for the given word problem is found as :x = 6.5.
know more about the word problems:
https://brainly.com/question/21405634
#SPJ1
complete question:
Twice the difference of a number and 4 is 5. Find the unknown number.
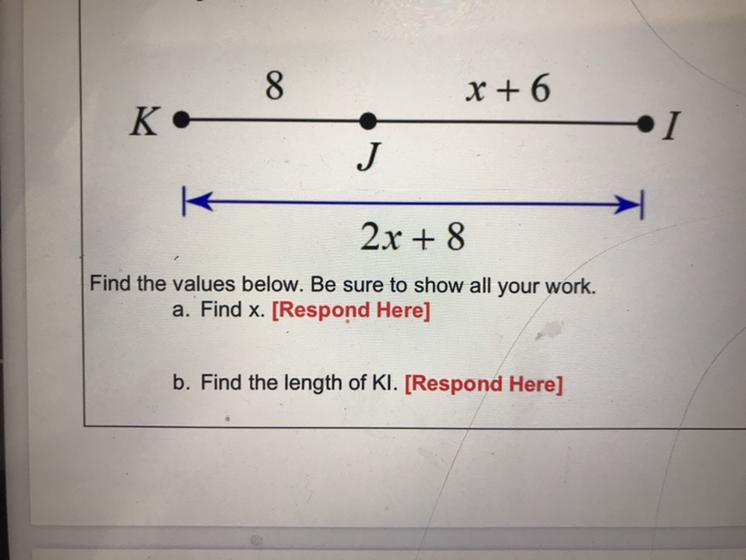
Segment KJ = 8, JI = x+6 and KI = 2x+8.
8
X + 6
K.
1
J
2x + 8
Find the values below. Be sure to show all your work.
a. Find x. [Respond Here]
b. Find the length of KI. [Respond Here]
Answers
Answer:
a). x = 6
b). Length of KI = 20 units
Step-by-step explanation:
From the picture attached,
a). Length of KI = length of KJ + length of JI
By substituting lengths of the segments given in the picture,
(2x + 8) = 8 + (x + 6)
2x + 8 = x + 14
2x - x = 14 - 8
x = 6
b). Length of KI = (2x + 8)
By substituting x = 6 in the expression,
Length of KI = 2(6) + 8
= 12 + 8
= 20 units
If the sum of an infinite geometric series is \( \frac{15625}{24} \) and the common ratio is \( \frac{1}{25} \), determine the first term. Select one: a. 625 b. 3125 c. 25 d. 125
Answers
The first term of the infinite geometric series is 625.Let's dive deeper into the explanation.
We are given that the sum of the infinite geometric series is \(\( \frac{15625}{24} \)\)and the common ratio is\(\( \frac{1}{25} \).\)The formula for the sum of an infinite geometric series is \(\( S = \frac{a}{1 - r} \)\), where \( a \) is the first term and \( r \) is the common ratio.
Substituting the given values into the formula, we have \(\( \frac{15625}{24} = \frac{a}{1 - \frac{1}{25}} \).\)To find the value of \( a \), we need to isolate it on one side of the equation.
To do this, we can simplify the denominator on the right-hand side.\(\( 1 - \frac{1}{25} = \frac{25}{25} - \frac{1}{25} = \frac{24}{25} \).\)
Now, we have \(\( \frac{15625}{24} = \frac{a}{\frac{24}{25}} \).\) To divide by a fraction, we multiply by its reciprocal. So, we can rewrite the equation as \( \frac{15625}{24} \times\(\frac{25}{24} = a \).\)
Simplifying the right-hand side of the equation, we get \(\( \frac{625}{1} = a \).\)Therefore, the first term of the infinite geometric series is 625.
In conclusion, the first term of the given infinite geometric series is 625, which corresponds to option (a).
learn more about geometric series here here
https://brainly.com/question/30264021
#SPJ11
The larget taco contained approximately 1 kg of onion for every 6. 6 kg grilled teak. The total weight of thee two ingredient wa 617. 3 kg. How many kilogram of each ingredient were ued?
Answers
The largest taco contained approximately 1 kg of onion for every 6. 6 kg grilled teak. then Amount of grilled steak used: 6.6 (79.17) = 538.356 kg
What is a unit amount in math?
When a price is expressed as a quantity of 1, such as $25 per ticket or $0.89 per can, it is called a unit price. If you have a non-unit price, such as $5.50 for 5 pounds of potatoes, and want to find the unit price, divide the terms of the ratio
1 k + 6.6 k = 617.3
Where “k” is a constant value, a multiplier.
Solving for k:
7.8 k = 617.3
k = 617.3 /7.8
k= 79.17
So:
Amount of onion used:
1 (79.17) = 79.17 kg
Amount of grilled steak used:
6.6 (79.17) = 538.356 kg
learn more about of ingredient here
https://brainly.com/question/15103492
#SPJ4
Cause
Effect
Muhammad began
preaching about his
beliefs in Mecca.
?
A. Mecca's poor citizens were treated more unfairly.
B. Mecca's leaders forced Muhammad to leave the city.
C. Muhammad was selected as the new ruler of Mecca.
D. Muhammad's followers attacked and destroyed Mecca.
SUBMIT
< PREVIOUS
Answers
Answer:
B. Mecca's leaders forced Muhammad to leave the city.
What is the probability that a randomly chosen college student exercises in the morning or afternoon? 0. 37 0. 39 0. 62 0. 76.
Answers
The probability that a randomly chosen college student exercises in the morning or afternoon is 0.76
We have given that the M be the event that the student exercises in the morning and A be the event that the student exercises in the afternoon.
To find : The probability that a randomly chosen college student exercises in the morning or afternoon
P(M) = 0.25+0.37 = 0.62
P(A) = 0.14+0.37 = 0.51
P(M and A) = 0.37
Now,
P(M or A) = P(M) + P(A) - P(M and A)
= 0.62 + 0.51 - 0.37
= 0.76
Hence, Option last 0.76 is the correct choice.
To learn more about the probability click here:
brainly.com/question/30034780
#SPJ4
What is the slope of the line whose equation is -2y = -4x + 5

Answers
Answer:
2
Step-by-step explanation:
Rearrange:
Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
-2*y-(-4*x+5)=0
STEP 1:
Pulling out like terms
1.1 Pull out like factors :
-2y + 4x - 5 = -1 • (2y - 4x + 5)
Equation at the end of step 1:
STEP 2:
Equation of a Straight Line
2.1 Solve -2y+4x-5 = 0
"y=mx+b" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis.
In this formula :
y tells us how far up the line goes
x tells us how far along
m is the Slope or Gradient i.e. how steep the line is
b is the Y-intercept i.e. where the line crosses the Y axis
The X and Y intercepts and the Slope are called the line properties. We shall now graph the line -2y+4x-5 = 0 and calculate its properties
Graph of a Straight Line :
Calculate the Y-Intercept :
Notice that when x = 0 the value of y is 5/-2 so this line "cuts" the y axis at y=-2.50000
y-intercept = 5/-2 = -2.50000
Calculate the X-Intercept :
When y = 0 the value of x is 5/4 Our line therefore "cuts" the x axis at x= 1.25000
x-intercept = 5/4 = 1.25000
Calculate the Slope :
Slope is defined as the change in y divided by the change in x. We note that for x=0, the value of y is -2.500 and for x=2.000, the value of y is 1.500. So, for a change of 2.000 in x (The change in x is sometimes referred to as "RUN") we get a change of 1.500 - (-2.500) = 4.000 in y. (The change in y is sometimes referred to as "RISE" and the Slope is m = RISE / RUN)
Slope = 2
Geometric figure: Straight Line
Slope = 2
x-intercept = 5/4 = 1.25000
y-intercept = 5/-2 = -2.50000
Answer:
2
Step-by-step explanation:
y=mx+b where m is the slope
to get y by itself you divide both sides by -2 resulting in
y= 2x+(-5/2)
2=m
suppose that the mean daily viewing time of television is hours per household. use a normal probability distribution with a standard deviation of hours to answer the following questions about daily television viewing per household.
(a) What is the probability that a household views television between 5 and 11 hours a day? (Round your answer to four decimal places.) (b) How many hours of television viewing must a household have in order to be in the top 3% of all television viewing households? (Round your answer to two decimal places.) (c) What is the probability that a household views television more than 3 hours a day? (Round your answer to four decimal places.)
Answers
The probability that a household watches more than 3 hours of television a day is 0.0478.
The mean daily viewing time of television is 8 hours per household. Use a normal probability distribution with a standard deviation of 3 hours to answer the following questions about daily television viewing per household.
(a) Probability that a household views television between 5 and 11 hours a day:P(5 < x < 11) = P(z < (11-8)/3) - P(z < (5-8)/3) = P(z < 1) - P(z < -1) = 0.8413 - 0.1587 = 0.6826(b) Hours of television viewing must a household have in order to be in the top 3% of all television viewing households:
The top 3% of all households correspond to z = 1.88. Therefore, the number of hours that a household must watch television to be in the top 3% is:1.88 = (x - 8) / 3x - 8 = 5.64x = 13.64
(c) Probability that a household views television more than 3 hours a day:P(x > 3) = P(z < (3-8)/3) = P(z < -5/3) = 0.0478.the probability that a household watches more than 3 hours of television a day is 0.0478.
For more such questions on probability
https://brainly.com/question/25839839
#SPJ11
Jacobey needs 32/3cups of milk to make one cheesecake. He is baking 4 cheesecakes for
the school bake sale. How many cups of milk does he need for the cheesecakes?
Answers
Answer: 14⅔
Step-by-step explanation: If he needs 3⅔ cups to make 1 cheese cake then he will need 11/3 ×4 cups to make 4 cakes
44/3 =14⅔
(Let me know if you mean 32/3 cups or 3⅔cups )
what are the two solutions to x( 2x - 5) = 0
Answers
Therefore you know that:
x = 0 and 2x - 5 = 0
2x - 5 = 0, solve for x
2x = 5, x = 5/2
Solution: x = 5/2, x = 0
What is the slope? A little bit of help. Due today at 11:59pm.

Answers
Answer:
2
Step-by-step explanation:
Answer:
The slope is 2
Step-by-step explanation:
(y2-y1)/(x2-x1)=m
Your Scenario:
(0-(-3))/(1.5-0)=2
The slope is 2 m=2
what is the measure of angle 6 if lines x and y are parallel and angle 7 measures 121 ?

Answers
Answer:
6=59° 1=6=8=3=59° 7=4=2=5=121°
the maintenance supervisor of an assembly line has two tool cabinets, one at each end of the assembly line. each morning, she walks from one end of the line to the other, and she is equally likely to begin the walk at either end. in the two tool cabinets are a total of six flashlights. at the beginning of her walk, the supervisor takes a flashlight (if one is available) from the tool cabinet at that location, and at the end of her walk, she leaves a flashlight (if she possesses one) from the tool cabinet at that location. model the movement of flashlights using a discrete-time markov chain.
Answers
A Markov chain models flashlight movement in an assembly line with seven states and transition probabilities. Steady-state probabilities are calculated to determine long-run proportions in each state.
Let's denote the state of the system by the number of flashlights in the tool cabinet at the starting end of the assembly line. Since there are two tool cabinets and a total of six flashlights, the state space consists of seven possible states: 0, 1, 2, 3, 4, 5, or 6 flashlights in the tool cabinet at the starting end.
At each step of the Markov chain, the supervisor takes a flashlight from the tool cabinet at the starting end (if one is available), and leaves a flashlight (if she possesses one) in the tool cabinet at the ending end. This means that the Markov chain is time-homogeneous, since the transition probabilities depend only on the current state and not on the time at which the transition occurs.
Let's calculate the transition probabilities between the states. If the supervisor starts at a state with k flashlights in the tool cabinet at the starting end, then there are 6 - k flashlights in the tool cabinet at the ending end. Therefore, the probability of moving to a state with j flashlights in the tool cabinet at the starting end is equal to the probability of taking a flashlight from the starting end (which is k/6 if k > 0) multiplied by the probability of leaving a flashlight at the ending end (which is (6 - k)/6 if j > 0) multiplied by the probability of starting at the ending end (which is 1/2 since the supervisor is equally likely to start at either end). Formally, we have:
P(k, j) = (k/6) * ((6 - k)/6) * (1/2) if j > 0
P(k, 0) = (6 - k)/6 * (1/2) if j = 0
Note that since the supervisor always takes a flashlight from the tool cabinet at the starting end, it is impossible to transition to a state with more flashlights at the starting end than the current state (i.e., P(k, j) = 0 if j > k).
We can represent the transition probabilities between the states using a transition probability matrix, which is a 7x7 matrix where element (i,j) is the probability of transitioning from state i to state j:
| P(0,0) P(0,1) P(0,2) P(0,3) P(0,4) P(0,5) P(0,6) |
| P(1,0) P(1,1) P(1,2) P(1,3) P(1,4) P(1,5) P(1,6) |
| P(2,0) P(2,1) P(2,2) P(2,3) P(2,4) P(2,5) P(2,6) |
| P(3,0) P(3,1) P(3,2) P(3,3) P(3,4) P(3,5) P(3,6) |
| P(4,0) P(4,1) P(4,2) P(4,3) P(4,4) P(4,5) P(4,6) |
| P(5,0) P(5,1) P(5,2) P(5,3) P(5,4) P(5,5) P(5,6) |
| P(6,0) P(6,1) P(6,2) P(6,3) P(6,4) P(6,5) P(6,6) |
We can fill in the entries of this matrix using the transition probabilities we calculated above.
For example, to find P(2,3), we use the formula we derived above, with k=2 and j=3:
P(2,3) = (2/6) * ((6 - 2)/6) * (1/2) = 1/12
Similarly, we can find all the other entries of the matrix.
Once we have the transition probability matrix, we can use it to calculate the steady-state probabilities of each state. These are the probabilities that the system will be in each state in the long run, assuming that the Markov chain has reached a steady state. The can be found by solving the equation:
πP = π
where π is a row vector of the steady-state probabilities and P is the transition probability matrix. Since the sum of the probabilities in any row of P is 1, we also have the normalization condition that the sum of the probabilities in π is 1.
We can solve for π using various methods, such as row reduction or matrix inversion. The steady-state probabilities tell us the long-run proportion of time that the system will spend in each state.
In summary, we can model the movement of flashlights using a discrete-time Markov chain with a state space of seven possible states (corresponding to the number of flashlights in the tool cabinet at the starting end), and transition probabilities that depend on the probabilities of taking and leaving flashlights at each end of the assembly line. We can calculate the steady-state probabilities of each state, which tell us the long-run proportion of time that the system will spend in each state.
know more about Markov chain here: brainly.com/question/30998902
#SPJ11
How to do this answer 6789×346
Answers
Answer:
2348994
Step-by-step explanation:
6789 x 346= 2348994
Hope this helps! Please mark brainiest!!!
Answer:
2348994
Step-by-step explanation:
last year, Austin had $30,000 to invest he invested some of it an account that paid 8% simple interest per year,and she invest the rest in a bank account that paid 10% simple interest per year.after one year, he receives a total of $2,680 to invest.how much did he and invest in each account?first account:____$second account:___$
Answers
We can solve this problem using a system of linear equations, have in mind the expression for simple interest:
\(\begin{gathered} I=\text{prt} \\ I=\text{interest} \\ p=\text{principal} \\ r=\text{rate in decimal form} \\ t=\text{time in years} \end{gathered}\)Let x be the principal invested on the first account.
Let y be the principal invested on the second account.
\(\begin{gathered} x+y=30,000\rightarrow\operatorname{Re}present\text{ total invested (1)} \\ 0.08x+0.1y=2,680\rightarrow\operatorname{Re}present\text{ the rates and interest earned }(2) \end{gathered}\)We can solve the system by the method of substitution, isolate the variable y in equation (1):
\(y=30,000-x\text{ (1)}\)Now, substitute (1) into equation (2) to get x-value:
\(\begin{gathered} 0.08x+0.1(30,000-x)=2,680 \\ 0.08x+3,000-0.1x=2,680 \\ -0.02x=2,680-3,000 \\ -0.02x=-320 \\ x=\frac{320}{0.02} \\ x=16,000 \end{gathered}\)Austin invested $16,000 on the first account.
Then, substitute the x-value in the equation (1) to get y-value:
\(\begin{gathered} y=30,000-16,000 \\ y=14,000 \end{gathered}\)Austin invested $14,000 on the second account.
