Answers
Answer:
which one is h because if i don't know which is h it cant solve a
Step-by-step explanation:
Answer:
A=2h, h∈ℝ
Step-by-step explanation:
Multiply both sides of the equation by 2.
2h=A
Swap the sides of the equation
A=2h
Related Questions
If f and g are continuous functions with f(0) = 2 and the following limit, find g(0). lim_(x->0)[2 f(x) - g(x)] = -3
Answers
We have by distributivity of limits over sums, and continuity of \(f(x)\) and \(g(x)\), that
\(\displaystyle \lim_{x\to0} \bigg(2f(x) - g(x)\bigg) = 2 \lim_{x\to0} f(x) - \lim_{x\to0} g(x) = 2 f(0) - g(0)\)
Given \(f(0)=2\), it follows that
\(2^2 - g(0) = -3 \implies g(0) = \boxed{7}\)
What is the measure of angle y?
I need help I’m being timed plz

Answers
Answer:
y=2, angle c=55, line AB is 2, line BC, is 2 angle X is 35. also fun fact that test is messed up because X is the angle not Y so either you may want to tell someone about that.
Step-by-step explanation:
Question 2. (30 points): Consider the following linear program: maxx s.t. z=4x1+3x2+3x32x1+2x2+x3≤4,x1+3x2+x3≤9,x1,x2,x3≥0. Write down the dual LP, graphically solve the dual LP, and then use complimentary slackness conditions to find the set of optimal solutions of the primal LP.
Answers
The optimal solution for the primal LP is x1 = 0, x2 = 2, x3 = 2, with a maximum value of z = 16.
Let's start by writing down the dual LP. The dual LP is obtained by interchanging the roles of variables and constraints in the primal LP. The dual variables corresponding to the constraints are y1 and y2, representing the multipliers for the first and second constraint, respectively. The objective function of the dual LP is given by minimizing 4y1 + 9y2, and the dual LP subject to the dual constraints is as follows:
min 4y1 + 9y2 subject to:
2y1 + y2 ≥ 4
3y1 + 3y2 ≥ 3
y1, y2 ≥ 0
To graphically solve the dual LP, we can plot the feasible region defined by the dual constraints and find the point that minimizes the objective function. By solving the dual LP, we obtain y1 = 1/3 and y2 = 2/3, with a minimum value of 10/3. Now, using the complementary slackness conditions, we can find the set of optimal solutions for the primal LP. The conditions state that for any optimal solution, the product of the primal constraint and the dual variable must be zero. Since the primal constraints are inequalities, we consider them as equalities to check the conditions. For the first constraint, 2x1 + 2x2 + x3 = 4, we have y1(2x1 + 2x2 + x3 - 4) = 0, which gives y1 = 0. Similarly, for the second constraint, x1 + 3x2 + x3 = 9, we have y2(x1 + 3x2 + x3 - 9) = 0, which gives y2 = 0. Hence, the optimal solution for the primal LP is x1 = 0, x2 = 2, x3 = 2, with a maximum value of z = 16, satisfying the complementary slackness conditions.
Learn more about variables here: brainly.com/question/30288589
#SPJ11
Given 2x² = -8, x is
A) -2
B) 2
C) 2i or -2i
B) 4i or -4i
NO LINKS!!!
Answers
Answer:
2x^2=-8
2x^2/2=-8/2
x^2=-4
x=2
Step-by-step explanation:
HOPE THAT THIS IS HELPFUL.
HAVE AN AWESOME DAY.
a quadratic function f(x) is graphed in the xy-coordinate plane in which wuadrant eould the vertex of f (x+3)+2
Answers
Answer:
The vertex is located on the x-axis between the second and third quadrants
Step-by-step explanation:
Whereby the function is f(x) = (x + 3)², we have;
f(x) = (x + 3)² = x² + 6·x + 9
The vertex, (h, k), of the quadratic function given in general form, a·x² + b·x + c is found as follows;
h = -b/(2·a) and k = f(h)
Therefore by comparison of the given quadratic function and the general form of a quadratic function, we have;
a = 1, b = 6, c = 9
h = -6/(2 × 1) = -3
k = f(-3) = (-3)² + 6 × (-3) + 9 = 0
The vertex (h, k) = (-3, 0)
Therefore, the location of the vertex is on the x-axis axis between the second and the third quadrant.
What are the sum of all the factors of 50 which are between 1 and 50. A. 42B. 2550C. 92D. 15
Answers
Factors of 50 are the numbers which on dividing 50 leave no remainder. 50 is a composite number, therefore, it has more than 2 factors.
We can get the factors of 50 by Prime Factorization. We can draw a factor tree to get the prime factors of 50 as shown below:
Therefore, the prime factors are:
\(2,5,5\)Hence, the other factors are:
\(\begin{gathered} 2\times5=10 \\ 5\times5=25 \end{gathered}\)Therefore, the factors of 50, including 1 and 50, are:
\(1,2,5,10,25,50\)The question asks to sum all the factors between 1 and 50. This means that 1 and 50 are not included in the sum.
Therefore, the sum will be:
\(\Rightarrow2+5+10+25=42\)The correct option is OPTION A.

Why do we express rational numbers as decimals?
Answers
Answer:
they can be represented as a ratio of two integers.
Step-by-step explanation:
the number of 9's in the denominator should be the same as the number of digits In the reapeated block.
Find the measure of angle BEC
A) 10 degrees
B)60 degrees
C) 80 degrees
D) 100 degrees

Answers
Answer:
80°
Step-by-step explanation:
Apply vertically opposite angles,
∠BEC = ∠GEA = 8x°
∠GEC = ∠BEA = (4x+60°)
To find x, apply angles at a point,
8x + 8x + (4x+60°) + (4x+60°) = 360°
16x + 2(4x+60°) = 360°
16x + 8x + 120° = 360°
24x = 240
x = 10
To find ∠BEC (8x°),
8 × 10 = 80°
ik hows it feels when u need brainliest so 2+2=
Answers
Answer:
4
Step-by-step explanation:
hope this helps!
Why everyone ignore me:/ plz help
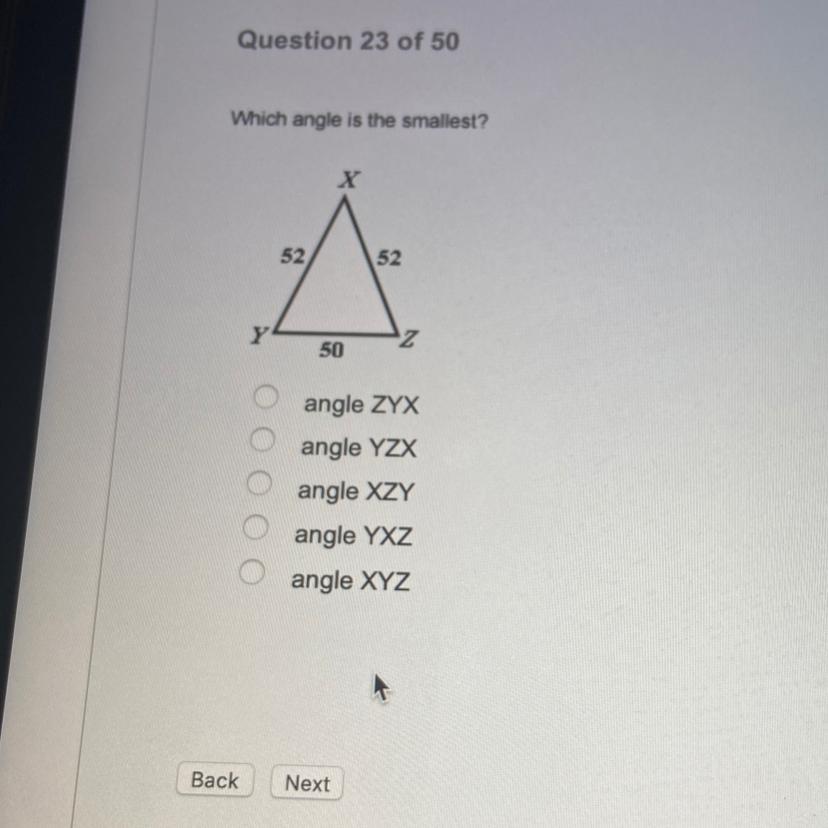
Answers
Answer:
D. YXZ is the smallest
Step-by-step explanation:
brainliest tambien
What is the slope of the line?

Answers
Answer:
-2/3
Step-by-step explanation:
Visibly we can see the line passes through (0,3) and (3,1)
The equation for slope is \(\frac{y_{1}-y_{2}}{x_{1}-x_{2}} = \frac{3-1}{0-3}= \frac{-2}{3}\)
I hope this helps! :)
Answer:
Slope = -2/3
Step-by-step explanation:
Rise over run, pick one point of intersection
Go up 2, go to the left until you reach another point of intersection, which is 3 units.
whatare the new coordinates of point R arter polygon QXYZR is rotated 180° and translated 3 units left?
step by step answer

Answers
The image of the point after the transformations is (0, -2)
What are the new coordinates of R?We can see that the original coordinates of point R are at (-3, 2).
A rotation of 180° means that we need to change the signs of the two components, then we will get (3, -2)
Finally, we apply a translation of 3 units to the left, so we need to subtract 3 units from the x-component of the point.
Then we will get (3 - 3, -2) = (0, -2)
That is the image of the transformations.
Learn more about transformations:
https://brainly.com/question/4289712
#SPJ1
divide milk and coffee, each person gets the same amount of milk coffee but different proportions, one of them has 1/ 4 cups of coffee and 1/6 of milk, for a total of 8 oz. what is the total number of people?
Answers
The possible number of person is 5.
Linear equation: an equation in which there is only one variable present. It is of the form Ax + B = 0, where A and B are any two real numbers and x is an unknown variable that has only one solution
Let,
The total amount of coffee= c
The total amount of milk = m
Total number of person = p
according to the question, c and m can't be .
Given,
Total amount of milk and coffee is 8 oz.
so,
\(\frac{c}{4} +\frac{m}{6} =8\\\)
\(\frac{3c+2m}{12} =8\)
So, this is linear equation.
3c+2m=8×12
\($$ \\$3 \mathrm{c}+2 \mathrm{~m}=96$\)
and
\(\eq\)\(c+m=8p\)
2(c+m) = 8p×2
\(2c+2m=24p\) ...(2)
By equation 1 and 2
\(3c+2m=96\\ 2m=96-3c\\ 2c+2m=16p\\ 2c+96-3c=16p\\96-c=16p\\96=16p+c\\\)
16p and 96 both are divisible by 16
So, let c =16k
Now 3c+2m =96
3(16k) +2m= 96
48k =2m= 96
k can't be 0, otherwise c is 0 and k cannot be 2, otherwise m is 0. Therefore k must be 1,
\(48+2m=96\\2m=96-48\\2m=48\\m=\frac{48}{2} \\m=24\)
BY putting m=24 in equation (1)
\(3c+2m=96\\3c+2(24)=96\\3c+48=96\\3c=96-48\\3c=48\\c=\frac{48}{3} \\c=16\)
Therefor, the number of person is 5
More information: brainly.in/question/25201905
#SPJ4
Find f(5) for f(x)=1/4 (2)^x
Answers
f(5) = 1/4(2)^5
f(5) = 1/4 (32)
f(5) = 8
answer
A. 8
HELPPP ME PLEASEEEE asappp

Answers
Answer:
B.) √3/2
Step-by-step explanation:
Answer:
B
Step-by-step explanation:
For questions like this I recommend memorizing the Unit Circle, but for the sake of calculations here's how I do it using a calculator
cos(30) = 0.866025.....
So now I'll just go through the answers and see which is equivalent
A= 1.73...
B= 0.866025....
C=0.57735....
D=0.5
E=0.7071.....
F=1
You can see that B is equivalent.
The midpoint of AB is M(2,-2). If the coordinates of A are (8,1), what are the
coordinates of B?
Answers
Answer:
B (-4, -5)
Step-by-step explanation:
A midpoint has to be exactly in the middle making the line split equally. I used Desmos to get my answer (it's a graphing calculator). And the line was slanted. Hope it's right! Plz tell is not!
I am unsure how to solve this problem and what formula

Answers
SOLUTION:
The z-score is gotten as;
\(Z=\frac{x-\mu}{\frac{\sigma}{\sqrt{n}}}\)Inserting, the values we have;
\(Z=\frac{7-8}{\frac{3}{\sqrt{25}}}=-1.67\)Thus, using a significance level of 0.05;
Thus, the answer is OPTION C
Find the perimeter and area of a rectangle whose width is \(3-\sqrt{8}\) and whose length is \(2+2\sqrt{2}\)
Answers
Calculations:
![Find the perimeter and area of a rectangle whose width is [tex]3-\sqrt{8}[/tex] and whose length is [tex]2+2\sqrt{2}[/tex]](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/6FBI45jJNZacDOh0G6Sk3YjsIOkTceu0.png)
IM GIVING 40 POINTS!
There is a stack of 10 cards, each given a different number from 1 to 10. Suppose we select a card randomly from the stack, replace it, and then randomly select another card. What is the probability that the first card is an odd number and the second card is less than 4? Write your answer as a fraction in the simplest form
Answers
Answer:
There are 10 cards in the stack, and 5 of them are odd (1, 3, 5, 7, and 9). There are 3 cards (1, 2, and 3) that are less than 4. Since we are replacing the first card before selecting the second, the outcomes are independent and we can multiply the probabilities of each event.
The probability of selecting an odd card on the first draw is 5/10, or 1/2.
The probability of selecting a card less than 4 on the second draw is 3/10, since there are 3 cards that meet this condition out of a total of 10.
Therefore, the probability of selecting an odd card on the first draw and a card less than 4 on the second draw is:
(1/2) x (3/10) = 3/20
So the probability of selecting an odd card on the first draw and a card less than 4 on the second draw is 3/20.
Step-by-step explanation:
Answer:
3/20.
Step-by-step explanation:
To find the probability of two independent events happening together, we multiply their individual probabilities. The probability of the first card being an odd number is 5/10, because there are 5 odd numbers out of 10 cards. The probability of the second card being less than 4 is 3/10, because there are 3 cards (1, 2, and 3) that are less than 4 out of 10 cards. Therefore, the probability of the first card being an odd number and the second card being less than 4 is:
5/10 x 3/10 = 15/100
We can simplify this fraction by dividing both the numerator and denominator by 5:
15/100 = 3/20
So, the final answer is 3/20.
Received message. To find the probability of two independent events happening together, we multiply their individual probabilities. The probability of the first card being an odd number is 5/10, because there are 5 odd numbers out of 10 cards. The probability of the second card being less than 4 is 3/10, because there are 3 cards (1, 2, and 3) that are less than 4 out of 10 cards. Therefore, the probability of the first card being an odd number and the second card being less than 4 is: 5/10 x 3/10 = 15/100 We can simplify this fraction by dividing both the numerator and denominator by 5: 15/100 = 3/20 So, the final answer is 3/20.
Find the first and second derivatives of the function. (Factor your answer completely.)
g(u) = u(2u − 3)^3
g ' (u) = g'' (u) =
Answers
The first derivative of the function `g(u) = u(2u - 3)^3` is `g'(u) = 6u(2u - 3)^2 + (2u - 3)^3`. The second derivative of the function is `g''(u) = 12(u - 1)(2u - 3)^2`.
Given function: `g(u)
= u(2u - 3)^3`
To find the first derivative of the given function, we use the product rule of differentiation.`g(u)
= u(2u - 3)^3`
Differentiating both sides with respect to u, we get:
`g'(u)
= u * d/dx[(2u - 3)^3] + (2u - 3)^3 * d/dx[u]`
Using the chain rule of differentiation, we have:
`g'(u)
= u * 3(2u - 3)^2 * 2 + (2u - 3)^3 * 1`
Simplifying:
`g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`
To find the second derivative, we differentiate the obtained expression for
`g'(u)`:`g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`
Differentiating both sides with respect to u, we get:
`g''(u)
= d/dx[6u(2u - 3)^2] + d/dx[(2u - 3)^3]`
Using the product rule and chain rule of differentiation, we have:
`g''(u)
= 6[(2u - 3)^2] + 12u(2u - 3)(2) + 3[(2u - 3)^2]`
Simplifying:
`g''(u)
= 12(u - 1)(2u - 3)^2`.
The first derivative of the function `g(u)
= u(2u - 3)^3` is `g'(u)
= 6u(2u - 3)^2 + (2u - 3)^3`. The second derivative of the function is `g''(u)
= 12(u - 1)(2u - 3)^2`.
To know more about derivative visit:
https://brainly.com/question/29144258
#SPJ11
The first derivative of g(u) is g'(u) = (2u - 3)³ + 6u(2u - 3)², and the second derivative is g''(u) = 12(2u - 3)² + 12u(2u - 3).
Using the product and chain ruleFirst, let's find the first derivative:
g'(u) = (2u - 3)³ * d(u)/du + u * d/dx[(2u - 3)³]
Using the chain rule, we can differentiate (2u - 3)³ and u as follows:
d(u)/du = 1
d/dx[(2u - 3)³] = 3(2u - 3)² * d(2u - 3)/du
= 3(2u - 3)² * 2
Plugging these values back into the equation for g'(u), we have:
g'(u) = (2u - 3)² + u * 3(2u - 3)² * 2
= (2u - 3)³ + 6u(2u - 3)²
Simplifying the expression, we have:
g'(u) = (2u - 3)³ + 6u(2u - 3)²
Now, let's find the second derivative:
g''(u) = d/dx[(2u - 3)³ + 6u(2u - 3)²]
Using the chain rule and product rule, we can differentiate each term:
d/dx[(2u - 3)³] = 3(2u - 3)² * d(2u - 3)/du
= 3(2u - 3)² * 2
d/dx[6u(2u - 3)²] = 6(2u - 3)² + 6u * d/dx[(2u - 3)²]
= 6(2u - 3)² + 6u * 2(2u - 3)
The Second derivativePlugging these values back into the equation for g''(u), we have:
g''(u) = 3(2u - 3)² * 2 + 6(2u - 3)² + 6u * 2(2u - 3)
= 6(2u - 3)² + 6(2u - 3)² + 12u(2u - 3)
= 12(2u - 3)² + 12u(2u - 3)
Simplifying the expression further, we have:
g''(u) = 12(2u - 3)² + 12u(2u - 3)
Therefore, the first derivative of g(u) is g'(u) = (2u - 3)³ + 6u(2u - 3)², and the second derivative is g''(u) = 12(2u - 3)² + 12u(2u - 3).
Learn more on differentiation : https://brainly.com/question/25081524
#SPJ4
What is the value of K ?

Answers
Answer:
the answer is A K= -2.5
Step-by-step explanation:
i did the problem
How do you read a graph on a coordinate plane?
Answers
The x-coordinate is represented by the number of units that we move left or right after starting at the origin.
What is meant by coordinate plane ?A Cartesian coordinate system in a plane is a system of coordinates where each point is given a unique set of numerical coordinates.which are the signed distances from two fixed perpendicular oriented lines to the point, measured in the same unit of length. Every point on a coordinate plane has an x coordinate and a y coordinate, which are both written as (x, y). The coordinate (3,2) has an x-coordinate of 3 and a y-coordinate of 2. By applying the distance formula, this distance can be determined. D = (x 2 x 1) 2 + (y 2 y 1) 2 can be used to calculate the distance between two points (x 1, y 1) and (x 2, y coordinate plane? 2).To learn more about coordinate plane refer to:
brainly.com/question/27481419
#SPJ4
The radius of a right circular cylinder is decreased by $20\%$ and its height is increased by $25\%$. What is the absolute value of the percent change in the volume of the cylinder
Answers
The absolute value of the percent change in the volume of the cylinder is 20%.
When the radius of a right circular cylinder is decreased by 20%, its new radius becomes 0.8 times the original radius (1 - 0.20 = 0.8).
Likewise, when its height is increased by 25%, its new height becomes 1.25 times the original height (1 + 0.25 = 1.25).
The volume of a right circular cylinder is given by the formula V = πr²h, where V is the volume, r is the radius, and h is the height. Let V₁ be the original volume, and V₂ be the new volume after the changes.
V₁ = π(r)²(h) and V₂ = π(0.8r)²(1.25h)
V₂ = π(0.64r²)(1.25h) = 0.8πr²h
Thus, the new volume is 0.8 times the original volume. This represents a 20% decrease in volume (1 - 0.8 = 0.20 or 20%). So, the absolute value of the percent change in the volume of the cylinder is 20%.
In summary, decreasing the radius by 20% and increasing the height by 25% results in a 20% decrease in the volume of the right circular cylinder.
Know more about right circular cylinder here:
https://brainly.com/question/2963891
#SPJ11
Jada keeps 175 hair beads in a storage box. She chooses a bead without looking,notes what color it is, and returns it to the box. She does this several times. The table shows the results
Answers
15 POINTS! will be selecting Brainliest!
How do I do this? Please give step-by-step answers + "work"- will be selecting Brainliest!

Answers
please helppp
(literally posting my entire math lesson)

Answers
Answer:
B
Step-by-step explanation:
Point B is located 6.5 tenths left of -8.
Answer:
Point B
Step-by-step explanation:
If you count 5 steps backward from -8, you land in the direct middle of -9 and -8. You can also count 5 steps forward from -9, but it doesn't change that the number represented is -8.5. Now focus on the distance from -8.5 to -9 (because between that distance are the points that we might be using). You repeat the same process used above, so if you half the distance between -8.5 and -9 then you'll get -8.75. As we can see, Point A is the closest to -8.75 compared to Point B. It wouldn't make sense to choose Point B because as we mentioned before, Point A is now most certainly not -8.65. Point B represents that number the best.
≧◡≦
Mocha here! If this answer helped you, please consider giving it brainliest because I would appreciate it greatly. Have a wonderful day!
Shelly drives 60 miles per hour for 2½ hours how far does she travel?
Answers
Answer:
she drove 150 miles
Step-by-step explanation:
Answer:
150 miles
Step-by-step explanation:
v= 60mph
t= 2.5 hours
We know that,
D=RT, distance equals rate times time.
Since you are traveling at 60 mph, the rate,
for 2.5 hours, the time, or equally 5/2 hours.
Substitute the value of r and t
d= 60 * 5/2
d= 150 miles
Therefore, if you are driving 60 miles per hour for 2.5 hours you will be covering a distance of 150 miles
5. suppose a normal distribution has a mean of 4 and a standard deviation of 1.5. what is the z-score of x
Answers
If a normal distribution has a mean of 4 and a standard deviation of 1.5. what is the z-score of x= 5.5 is 1
The mean of the normal distribution = 4
Standard deviation of the normal distribution = 1.5
The value of x = 5.5
The z-score of the normal distribution = The mean of the normal distribution / Standard deviation of the normal distribution
Substitute the values in the equation
The z-score of the normal distribution = (5.5 - 4) / 1.5
Substract the terms
= 1.5 / 1.5
= 1
Hence, if a normal distribution has a mean of 4 and a standard deviation of 1.5. what is the z-score of x= 5.5 is 1
The complete question is:
suppose a normal distribution has a mean of 4 and a standard deviation of 1.5. what is the z-score of x = 5.5
Learn more about z-score here
brainly.com/question/15016913
#SPJ4
Solve for x:
(a) 4x - 21 = 5 - 9x
Answers
Answer:
X = 2
Step-by-step explanation:
First we'll need to simplify this equation:
Add 9x on both sides:
13x - 21 = 5
Add 21 on both sides:
13x = 26
Divide 26/13
26/13 = 2
X=2
(You can check this yourself by plugging x into the equation)
In order to summarize qualitative data, a useful tool is a____________.
A) histogram
B) stem-and-leaf diagram
C) scattergram
D) frequency distribution
Answers
A (A) histogram is a useful tool for condensing qualitative data.
What is a histogram?An effective tool for summarizing qualitative data is a histogram.
The distribution of numerical data is roughly depicted by a histogram.
Karl Pearson was the person who first coined the phrase.
The first stage in creating a histogram is to "bin" (or "bucket") the range of values, divide it into a series of intervals, and then count the number of values that fall into each interval.
The bins are often defined as a series of discrete intervals that don't overlap.
The bins (intervals) must be close together and frequently, though not always, have the same size.
Therefore, a (A) histogram is a useful tool for condensing qualitative data.
Know more about a histogram here:
https://brainly.com/question/2962546
#SPJ4
