Answers
Answer:
5.6
Step-by-step explanation:
Answer:
5.6
Step-by-step explanation:
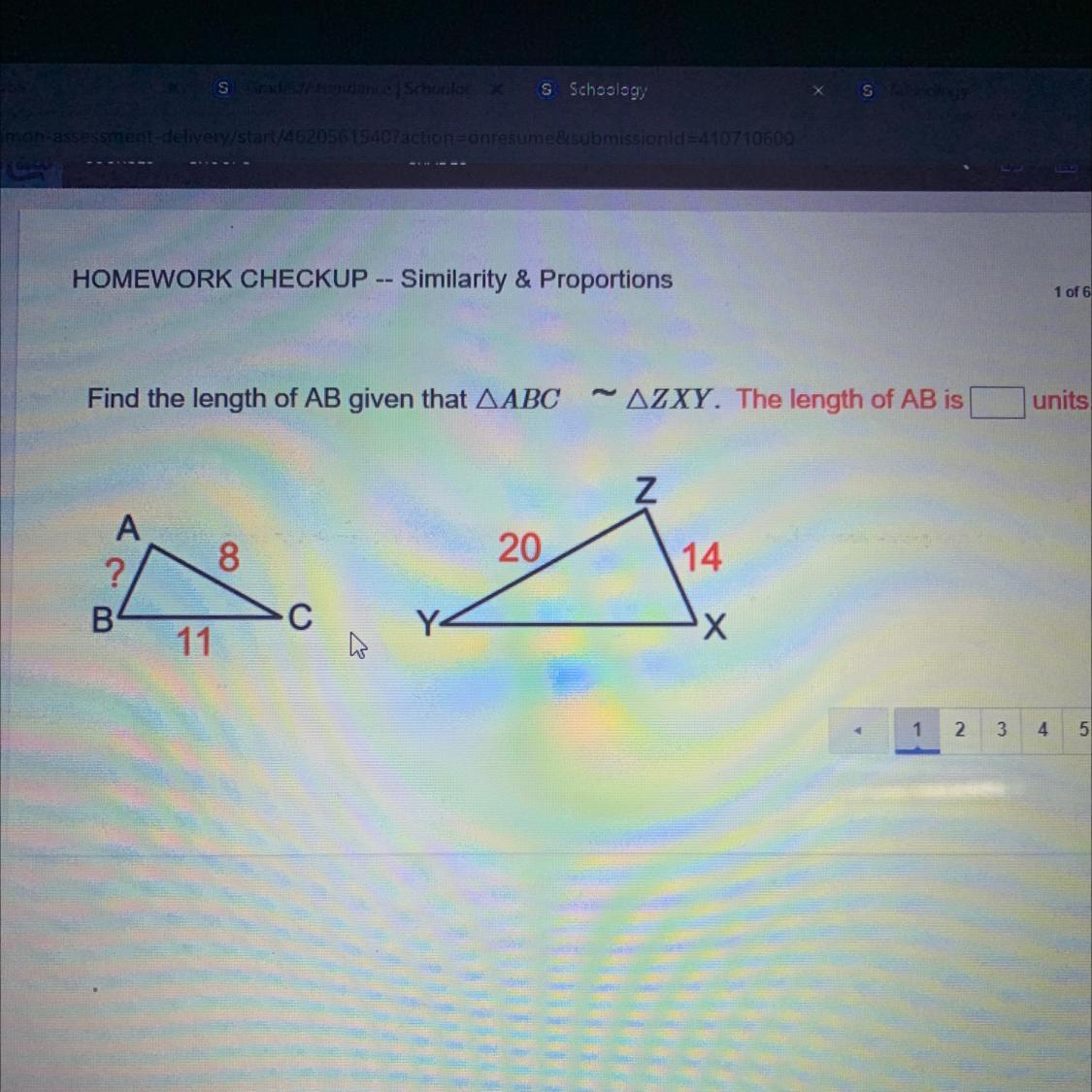
8 : 20
? : 14
(cross multiply)
8 * 14
20 = 5.6
Related Questions
I need an answer! NO LINKS PLS! il give brainlist

Answers
The more the better! Mark with crown please!
Explain how to find the y-intercept on a graph.
Answers
Answer:
It's called the "y intercept" and it's the y value of the point where the line intersects the y- axis. For this line, the y-intercept is "negative 1." You can find the y-intercept by looking at the graph and seeing which point crosses the y axis. This point will always have an x coordinate of zero.
Step-by-step explanation:
Answer:
It's called the "y intercept" and it's the y value of the point where the line intersects the y- axis. For this line, the y-intercept is "negative 1." You can find the y-intercept by looking at the graph and seeing which point crosses the y axis. This point will always have an x coordinate of zero.
Step-by-step explanation:
I hope I helped!!!

can u answer this for me pls i really need help

Answers
a sign in the elevator of a college library indicates a limit of 16 persons. in addition, there is a weight limit of 2,500 pounds. assume that the average weight of students, faculty, and staff at this college is 155 pounds, that the standard deviation is 29 pounds, and that the distribution of weights of individuals on campus is approximately normal. a random sample of 16 persons from the campus will be selected.
Answers
The probability that a randomly selected group of 16 individuals from the campus will be selected is 0.8023 or 80.23%
Based on the sign in the elevator of the college library, the limit of 16 persons and weight limit of 2,500 pounds need to be adhered to. To ensure compliance with both limits, we need to consider both the number of people and their weight.
Assuming that the distribution of weights of individuals on campus is approximately normal with an average weight of 155 pounds and a standard deviation of 29 pounds, we can use this information to estimate the total weight of a group of 16 randomly selected individuals.
The total weight of a group of 16 individuals can be estimated as follows:
Total weight = 16 x average weight = 16 x 155 = 2480 pounds
To determine if this total weight is within the weight limit of 2,500 pounds, we need to consider the variability in the weights of the individuals. We can do this by calculating the standard deviation of the total weight using the following formula:
Standard deviation of total weight = square root of (n x variance)
where n is the sample size (16) and variance is the square of the standard deviation (29 squared).
Standard deviation of total weight = square root of (16 x 29^2) = 232.74
Using this standard deviation, we can calculate the probability that the total weight of the group of 16 individuals is less than or equal to the weight limit of 2,500 pounds:
Z-score = (2,500 - 2,480) / 232.74 = 0.86
Using a standard normal distribution table or calculator, we can find that the probability of a Z-score less than or equal to 0.86 is approximately 0.8023.
Therefore, the probability that a randomly selected group of 16 individuals from the campus will comply with both the number and weight limits in the elevator of the college library is approximately 0.8023 or 80.23%.
To know more about probability click on below link :
https://brainly.com/question/14210034#
#SPJ11
Melanie is walking a path around a circular path to view all of the artwork painted on the cement edge. The circular fountain has a radius of 30 feet. If Melanie only walked around the fountain once, how far did she travel?
Answers
Step-by-step explanation:
The diameter is the line drawn that divides the circle into two while the circumference is the perimeter of the circle. Both are a measure of the radius of the circle.
The diameter D = 2r where r is the radius of the circle
The circumference = 2Πr = ΠD where Π = 22/7
Given that the circular fountain has a radius of 9.4 feet
Its diameter = 2 × 9.4 feet = 18.8 feet
The circumference = 22/7 × 18.8 feet
=59.09 feet
≈ 59.1 feet to the nearest tenth
each side of a square is increasing at a rate of 4 cm/s. at what rate (in cm2/s) is the area of the square increasing when the area of the square is 49 cm2?
Answers
The area of the square increasing with 56 cm²/s
Area or A = x²
where x represents one side of the square
The rate at which each side is increasing or dx/dt = 4 cm/s.
The area of the square is 49cm²
A = x²
x = √A
x = √49 = 7
Each side of the square or x = 7cm
We are trying to find the rate the area is changing, so dA/dt
A=x²
Take the derivative of the area equation with respect to time
dA/dt= 2x * dx/dt
Now plug in the values given to solve for dA/dt: x = 7 cm and dx/dt= 4 cm/s
2 (7) * (4) = 56 cm²/s
Therefore, the area of the square increasing with 56 cm²/s
To learn more about derivatives refer here
https://brainly.com/question/23819325
#SPJ4
Determine the value(s) of n .
P(3 n, n-7), Q(4 n, n+5), P Q=13
Answers
The value(s) of n are: n = -6 + sqrt(57)
n = -6 - sqrt(57)
So, the value of n can be expressed as either -6 plus the square root of 57 or -6 minus the square root of 57.
To determine the value(s) of n in the given problem, let's first understand the notation used. P(3n, n-7) represents a point with coordinates (3n, n-7), and Q(4n, n+5) represents a point with coordinates (4n, n+5).
The distance between two points can be found using the distance formula, which states that the distance between two points (x1, y1) and (x2, y2) is given by:
d = sqrt((x2 - x1)^2 + (y2 - y1)^2)
In this case, we are given that the distance between P and Q is 13, so we can set up the equation:
sqrt((4n - 3n)^2 + ((n+5) - (n-7))^2) = 13
Simplifying the equation, we get:
sqrt(n^2 + 12n + 12^2 + 2^2) = 13
Squaring both sides of the equation to eliminate the square root, we have:
n^2 + 12n + 144 + 4 = 13^2
n^2 + 12n + 148 = 169
Rearranging the equation, we get:
n^2 + 12n - 21 = 0
To solve this quadratic equation, we can use factoring, completing the square, or the quadratic formula. Factoring this equation might not be straightforward, so we can use the quadratic formula:
n = (-b ± sqrt(b^2 - 4ac)) / (2a)
For our equation, a = 1, b = 12, and c = -21. Substituting these values into the quadratic formula, we get:
n = (-12 ± sqrt(12^2 - 4(1)(-21))) / (2(1))
Simplifying further:
n = (-12 ± sqrt(144 + 84)) / 2
n = (-12 ± sqrt(228)) / 2
n = (-12 ± 2sqrt(57)) / 2
Simplifying and factoring out a common factor of 2:
n = -6 ± sqrt(57)
Therefore, the value(s) of n are:
n = -6 + sqrt(57)
n = -6 - sqrt(57)
So, the value of n can be expressed as either -6 plus the square root of 57 or -6 minus the square root of 57.
Know more about coordinates here:
https://brainly.com/question/32836021
#SPJ11
A simple random sample of 500 elements generates a sample proportion p= 0.81. Provide the 90% confidence interval for the population proportion (to 4 decimals). b.Provide 95% the confidence interval for the population proportion (to 4 decimals).
Answers
a) The 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b) The 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
To calculate the confidence intervals for the population proportion, we can use the formula:
Confidence Interval = sample proportion ± margin of error
The margin of error can be calculated using the formula:
Margin of Error = critical value * standard error
where the critical value is determined based on the desired confidence level and the standard error is calculated as:
Standard Error = \(\sqrt{((p * (1 - p)) / n)}\)
Given that the sample proportion (p) is 0.81 and the sample size (n) is 500, we can calculate the confidence intervals.
a. 90% Confidence Interval:
To find the critical value for a 90% confidence interval, we need to determine the z-score associated with the desired confidence level. The z-score can be found using a standard normal distribution table or calculator. For a 90% confidence level, the critical value is approximately 1.645.
Margin of Error = \(1.645 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0323
Confidence Interval = 0.81 ± 0.0323
≈ (0.7777, 0.8423)
Therefore, the 90% confidence interval for the population proportion is approximately (0.7777, 0.8423).
b. 95% Confidence Interval:
For a 95% confidence level, the critical value is approximately 1.96.
Margin of Error = \(1.96 * \sqrt{(0.81 * (1 - 0.81)) / 500)}\)
≈ 0.0363
Confidence Interval = 0.81 ± 0.0363
≈ (0.7737, 0.8463)
Thus, the 95% confidence interval for the population proportion is approximately (0.7737, 0.8463).
Learn more about confidence interval here:
brainly.com/question/32546207
#SPJ4
PART X: Lost at sea
Suddenly, during your race, a powerful thunderstorm strikes. A wave washes over your boat, shorting out your navigation devices. They wouldn't be much use anyhow, because the lightning is interfering with all communications in the area.
When the storm ends and the sea is calm, you're safe, because you observed all safety precautions, but you have no idea how far off course you are. However, you do know:
* The height of a nearby landmark, which you remember from the tourist center you visited yesterday.
> Mykonos: The light in the Armenistis Lighthouse is 604 feet above sea level.
* The length of your thumb - it's about 2 inches long.
* That you can estimate lengths of less than a foot pretty accurately (to the nearest inch).
1. First, you close one eye and hold your thumb up to block your view of the landmark. You move your thumb nearer and farther from your eye until it just covers the landmark.
Make a sketch showing overlapping triangles ΔEBT and ΔELH to illustrate this situation, where your eye is E, the base of your thumb is B, the tip of your thumb is T, the bottom of the landmark is L, and the top of the landmark is H.
2. Explain why ΔEBT~ΔELH
3. When your thumb covers the landmark, you estimate that it is 10 inches from your eye. Label your drawing with the known measurements.
4. Solve for EL, the distance from your eye to the landmark. Show all work and justify each step.
Answers
Answer: 1. Here is a sketch of the overlapping triangles ΔEBT and ΔELH:
H
/|
/ |
/ |
/ |
/ θ |
/____|L
E
|
|
|
|
T
|
|
|
|
B
2. ΔEBT~ΔELH because they have the same shape (both are right triangles with angle θ in common) and their corresponding sides are proportional. Specifically, angle θ is shared by both triangles, angle EBT is a right angle, and angle ELH is a right angle. Therefore, by the Angle-Angle Similarity Theorem, the two triangles are similar. Corresponding sides are proportional because EB/EL = BT/LH (by definition of similar triangles).
3. We are given that BT (the length of the thumb) is about 2 inches. We are also told that the distance from the eye to the landmark (EL) is unknown, but that the distance from the eye to the thumb (EB) is 10 inches (estimated by the person). We are given that LH (the height of the landmark) is 604 feet, or 604*12=7248 inches (since there are 12 inches in a foot). Therefore, we can label the diagram as follows:
7248
/|
/ |
/ | EL
/ |
/ θ |
/____|L
E
|10
|
|
|
T
| 2
|
|
|
|
B
4. To solve for EL, we use the fact that the triangles are similar: EB/EL = BT/LH. Substituting in the known values, we get:
10/EL = 2/7248
5. Multiplying both sides by EL and dividing both sides by 2, we get:
EL = 7248*5 = 36240 inches
Therefore, the distance from the eye to the landmark is 36240/12 = 3020 feet (rounded to the nearest foot).
Step-by-step explanation:
Graph the inequality in a coordinate plane. -X+4y>-12
Need help!!!

Answers
Answer:
Step-by-step explanation:
THE DARK IS GONNA BE RIGHT OVER LEWFT TO PLAY THE Gme
a password consists of four alphanumeric characters (case insensitive). a valid password must contain at least one digit and at least one letter. how many different passwords are there
Answers
There are 1,280,240 different passwords that meet the criteria of containing at least one letter and at least one digit, and consisting of four alphanumeric characters (case insensitive).
How to calculate the total number of different passwords?To calculate the total number of different passwords, we can break the problem down into several steps:
Step 1: Calculate the number of possible characters for each position in the password. Since the password consists of four alphanumeric characters, there are 26 letters (A-Z) and 10 digits (0-9) for each position.
Therefore, there are 36 possible characters for each position.
Step 2: Calculate the total number of possible passwords without any restrictions.
Since there are 36 possible characters for each position and the password has four positions, the total number of possible passwords without any restrictions is:
36 x 36 x 36 x 36 = 1,679,616
Step 3: Calculate the number of passwords that do not contain at least one digit or at least one letter.
To do this, we can calculate the number of passwords that do not contain any digits and subtract it from the total number of possible passwords, and then do the same for passwords that do not contain any letters.
The number of passwords that do not contain any digits is:
26 x 26 x 26 x 26 = 456,976
The number of passwords that do not contain any letters is:
10 x 10 x 10 x 10 = 10,000
However, we have to be careful not to double-count the passwords that do not contain both letters and digits.
The number of passwords that do not contain both letters and digits is:
26 x 26 x 10 x 10 = 67,600
So the total number of passwords that do not contain at least one digit or at least one letter is:
456,976 + 10,000 - 67,600 = 399,376
Step 4: Subtract the number of invalid passwords from the total number of possible passwords:
1,679,616 - 399,376 = 1,280,240
Therefore, there are 1,280,240 different passwords that meet the criteria of containing at least one letter and at least one digit, and consisting of four alphanumeric characters (case insensitive).
Learn more about calculate the total number of different passwords
brainly.com/question/17303313
#SPJ11
At its highest point, the elevation of a county is 5764 feet above sea level. At its lowest point, the elevation of the county is 9 feet below sea level.
Answers
(a) The expression to represent the difference between the elevations is 5764 - ( - 9).
(b) The answer will be a positive integer.
(c) The difference between the highest and lowest point is 5773 feet.
The elevation of a county is 5764 feet above sea level.
The elevation of the county is 9 feet below sea level at the lowest point.
(a) The highest point = 5764 feet
The lowest point = 9 feet
Then the difference between the highest and the lowest point will be:
difference = Highest - lowest
difference = 5764 - ( - 9)
(b) The answer will be written as a positive integer.
(c) The difference between the highest and lowest points of the county will be:
difference = Highest - lowest
difference = 5764 - ( - 9)
difference = 5764 + 9
difference = 5773 feet
Learn more about elevation here:
https://brainly.com/question/18671990
#SPJ9
The complete question is mentioned below:
At its highest point, the elevation of a county is 5764 feet above sea level. At its lowest point, the elevation of the county is 9 feet below sea level. Answer parts (a) through (c).
a. Write an expression using integers to represent the difference between the elevations.
b. Will the answer be written as a positive or negative integer?
c. What is the difference between the highest and lowest points of the county?
there are currently 63 million cars in a certain country, decreasing by 4.3 nnually. how many years will it take for this country to have 45 million cars? (round to the nearest year.)
Answers
It will take approximately 4 years for the country to have 45 million cars.
To find out how many years it will take for the country to have 45 million cars, set up an equation based on the given information.
Let's denote the number of years it will take as "t".
the number of cars is decreasing by 4.3 million annually. So, the equation becomes:
63 million - 4.3 million * t = 45 million
Simplifying the equation:
63 - 4.3t = 45
Now, solve for "t" by isolating it on one side of the equation. Let's subtract 63 from both sides:
-4.3t = 45 - 63
-4.3t = -18
Dividing both sides by -4.3 to solve for "t", we get:
t = (-18) / (-4.3)
t ≈ 4.186
Since, looking for the number of years, round to the nearest year. In this case, t ≈ 4 years.
Therefore, it will take approximately 4 years for the country to have 45 million cars.
Learn more about equation here:
https://brainly.com/question/10724260
#SPJ11
Helpppppppppppppppp plzzz

Answers
Answer:
$0.56, or 56¢.
Step-by-step explanation:
According to the picture, there are two dimes, two nickels, a penny, and a quarter.
A penny is worth $0.01.
A nickel is worth $0.05.
A dime is worth $0.10.
A quarter is worth $0.25.
2(0.1) + 2(0.05) + (0.01) + (0.25) = 0.2 + 0.1 + 0.01 + 0.25 = 0.3 + 0.26 = 0.56.
So, Vivian is using $0.56, or 56¢, to buy a toy. That's a cheap one!
Hope this helps!
Answer this math question for 10 points

Answers
Measure of angle:
∠A = 36.86°
∠B = 90°
∠C = 53.13 °
Measure of side ,
AB = 28
BC = 21
CA = 35
Given triangle ABC.
Right angled at B.
Now, using trigonometric ratios to find angle A , B , C .
Right angled at B : ∠B = 90°
Angle A,
SinA = 21/35
∠A = 36.86
Angle C,
SinC = 28/35
∠C = 53.13
Now measures of side.
To find the length of side use sine rule .
Sine rule:
a/sinA = b/sinB = c /sinC
a = opposite side of angle A .
b = opposite site of angle B .
c = opposite side of angle C.
AB = 28
BC = 21
CA = 35
Hence the sides and angles of the triangles are measured .
Know more about sine rule,
https://brainly.com/question/30339239
#SPJ1
In a middle-school mentoring program, a number of the sixth graders are paired with a ninth-grade student as a buddy. no ninth grader is assigned more than one sixth-grade buddy. if 1/3 of all the ninth graders are paired with 2/5 of all the sixth graders, what fraction of the total number of sixth and ninth graders have a buddy
Answers
The total fraction of sixth and ninth graders who have a buddy is (n + s)/5.
Let there be s sixth graders and n ninth graders. Since 2/5 of the sixth graders are paired with 1/3 of the ninth graders, we can set up the equation: (2/5)s = (1/3)n
Multiplying both sides of the equation by 15 gives us: 6s = 5n
Then, we can rewrite the equation as: s + n = 5n/6
We can simplify this equation to: s + n = (5/6)n + (5/6)s
Combining like terms on the right side of the equation gives us: s + n = (11/6)s + (5/6)n
Subtracting (5/6)n from both sides of the equation gives us: s + n - (5/6)n = (11/6)s
Combining like terms on the left side of the equation gives us: (6/6)s + (1/6)n = (11/6)s
Subtracting (11/6)s from both sides of the equation gives us: (1/6)n = -(5/6)s
Dividing both sides of the equation by (1/6) gives us: n = -(5/1)s
Multiplying both sides of the equation by (-1) gives us: n = (5/1)s
Dividing both sides of the equation by 5 gives us: n/5 = s/5
The fraction of sixth and ninth graders who have a buddy is equal to the number of ninth graders who have a buddy (n/5) plus the number of sixth graders who have a buddy (s/5). The total fraction of sixth and ninth graders who have a buddy is therefore: (n/5) + (s/5) = (n + s)/5.
To learn more about Fractions,
visit; brainly.com/question/10354322
#SPJ4
Use the Gauss-Seidel approximate solutions to method to find x1 + x2 +54x3 = 110 27x16x2x3 = = 85 6x1 + 15x2 + 2x3 = 72 with an error of less than 0.5% starting with zero as the initial values of x. Round-off intermediate values to 8 decimal places. Round-off answer to 6 decimal places. Reminder: Arrange the system to be Diagonally Dominant before iteration. x1 = 2.432175, x2 = 3.572041, x3 = 1.925848 x₁ = 2.425689, x2= 3.572945, x3 = 1.925951 none of the choices x1 = 2.425478, x2 = 3.573015, x3 = 1.925954 O x1 = 2.425492, x2= 3.573010, x3 = 1.925954
Answers
The shape with a series of parallel cross sections that are congruent circles is a cylinder.
The cross-section that results from cutting a cylinder parallel to its base is a circle that is congruent to all other parallel cross-sections. This is true for any plane that is perpendicular to the cylinder's base. The only shape that has parallel cross-sections that are congruent circles is a cylinder, for this reason.
Two parallel, congruent circular bases that lay on the same plane make up the three-dimensional shape of a cylinder. A curved rectangle connecting the bases makes up the cylinder's lateral surface. Congruent circles are produced when a cylinder is cut in half parallel to its base.
learn more about congruent circles
at brainly.com/question/9337801
#SPJ4
is 5+8x=y proportional or non proportional
Answers
Answer:
its proportional
Step-by-step explanation:
Find the sum of all angles of the quadrilateral if sides are in ratio 2:3:6:9
Answers
2 =
3 =
6 : 9 =
Step-by-step explanation:
Here are some solutions! Hope this helps.
-Lei
Use the washer method to determine the volume of the solid formed when the region bounded by y=x and y=x3 is rotated about the y-axis over the interval 0≤x≤1.
Answers
The volume of the solid using the washer method for the region bounded is equal to π /12 cubic units.
Washer method is one of the method to calculate the volume enclosed between two functions.
Here slice the region of revolution perpendicular to the axis of the given revolution.
Named it Washer Method as the slices obtained in this way forms washers.
Washer is a solid with a hole in the middle.
Volume = \(\int_{a}^{b}\) [(f(x))² - (g(x))²]dx
Volume of entire solid - volume of hole
Radius of washer represented by distance from the y-axis to the edge of given region
x for y=x
√y for y=x^3 over the interval 0≤x≤1.
Height of washer is same as width of region = dx.
Volume of washer
= \(\int_{0}^{1}\) π × [ (outer radius)²- (inner radius)² ]dx
= \(\int_{0}^{1}\) π × ( x² - x³ ) dx
= π [(x³/3) - ( x⁴ /4 ) ]\(|_{0}^{1}\)
= π ( 1/3 - 1/4)
= π( 4 - 3 ) / 12
= π /12 cubic units
Therefore, the volume of the solid formed for the region bounded is equal to π /12 cubic units.
Learn more about volume here
brainly.com/question/30453321
#SPJ4
help please, mainly with part b

Answers

Answer:
hope this answer helps you dear...take care and may u have a great day ahead!


At a wedding there were 40 people from gromms side and 56 people from bride's family at the wedding
find the ratio of the groom's family to the bride's family at the wedding
Answers
Answer:
5 : 7
Step-by-step explanation:
groom's side: 40
bride's side: 56
ratio groom to bride = 40/56 = 20/28 = 10/14 = 5/7
Answer: 5 : 7
Explanation- 50+56 Is 106. So 106- 10=96.
There is your answer 96.
Midyear on July 31st, the Digby Corporation's balance sheet reported: Total Liabilities of $25.862 million Cash of $2.010 million Total Assets of $43.091 million Total Common Stock of $1.270 million. What were the Digby Corporation's retained earnings?
Answers
Digby Corporation's retained earnings for the midyear on July 31st were $15.959 million.
What are the retained earnings?The retained earnings refer to the portion of the company's accumulated profits that have not been distributed to common stockholders.
We can compute the retained earnings are the difference between the total assets and total liabilities and common stock since common stock plus retained earnings are equal to stockholders' equity.
Digby Corporation
Balance SheetMidyear ended July 31st
Cash of $2.010 million
Total Assets = $43.091 million
Total Liabilities of $25.862 million
Total Common Stock of $1.270 million
Total liabilities and common stock = $27.132 million ($25.862 + $1.270)
Retained Earnings:Total Assets = $43.091 million
Less total liabilities and common stock $27.132 million
Retained earnings = $15.959 million ($43.091 - $27.132)
Learn more about the retained earnings at https://brainly.com/question/25631040.
#SPJ1
WILL GIVE BRAINLIEST , pls helppp .
When firefighters are trying to put out a fire, the rate at which they can spray water on the fire depends on the water pressure. You can find the flow rate f in gallons per minute using the equation, f = 120p, where p is the nozzle pressure in pounds per square inch.
What would the flow rate be if the pressure was 16 Ibs/in square?
MUST SHOW WORK
(A) 2.13
(B) 1,920
(C) 43.8
(D) 960
Answers
Answer:
B
Step-by-step explanation:
f=120p
f=120(16)
f= 1920
Salary Ron’s paycheck this week was $17.43 less than his paycheck last week. His paycheck this week was $103.76. How much was Ron’s paycheck last week?
Answers
Ron’s paycheck last week was $121.19. Given that Ron's paycheck this week was $17.43 less than his paycheck last week.
His paycheck this week was $103.76.
To find how much was Ron’s paycheck last week, we need to use the following formula. Let Ron’s paycheck last week be x. Then,x - 17.43 = 103.76.
To find x, add 17.43 to both sides of the equation, then we get;x - 17.43 + 17.43 = 103.76 + 17.43x = 121.19
Therefore, Ron’s paycheck last week was $121.19.Hence, the required answer is $121.19.
For more question on equation
https://brainly.com/question/22688504
#SPJ8
If two angles are supplementary to the same angle, then:
a. They are adjacent angles
b. They are congruent angles
c. They are complementary angles
d. They are congruent supplementary angles
Answers
The option D is the correct answer.
a. They are adjacent angles: Adjacent angles are angles that share a common side and vertex, but do not overlap. It is possible for two angles to be supplementary and adjacent, but it is not always the case. Therefore, option a is not the correct answer.
b. They are congruent angles: Congruent angles have the same measure. Two angles that are supplementary to the same angle can have different measures, so option b is not the correct answer.
c. They are complementary angles: Complementary angles are two angles that add up to 90 degrees. Since two angles that are supplementary to the same angle add up to 180 degrees, they cannot also be complementary. Therefore, option c is not the correct answer.
d. They are congruent supplementary angles: Congruent supplementary angles have the same measure and add up to 180 degrees. This is the correct answer because if two angles are supplementary to the same angle, their measures must be equal in order for their sum to be 180 degrees. Therefore, option d is the correct answer.
To summarize, if two angles are supplementary to the same angle, they are congruent supplementary angles because their measures are equal and add up to 180 degrees.
To know more about angles here::
brainly.com/question/10451301
#SPJ11
What are the 3 angle bisectors of a triangle intersect?.
Answers
The three angle bisector of a triangle intersect at a single point that point of concurrency of the angle of bisectors is called the incenter.
Given:
the 3 angle bisectors of a triangle intersect.
when three angle bisector of a triangle intersect then that point of concurrency is called incenter.
Incenter:
The incenter of a triangle is the intersection point of all the three interior angle bisectors of the triangle. In other words, it can be defined as the point where the internal angle bisectors of the triangle cross. This point will be equidistant from the sides of a triangle, as the central axis’s junction point is the center point of the triangle’s inscribed circle.
Incenter formula:
= (ax1+bx2+x3 / a+b+c , ay1+by2+y3 / a+b+c).
Learn more about the triangle here:
https://brainly.com/question/2773823
#SPJ4

evaluate the complex number (14 j3)1 − j6 (7−j8)−5 j11 . the complex number is represented as j .
Answers
The evaluation of the complex number results as 22 - (62/37)j
We are given two complex numbers to evaluate: (2 + j3/1 - j6) and (7 - j8/-5 + j11). To simplify the expression, let's work with one complex number at a time.
The first complex number, (2 + j3/1 - j6), can be written as follows: 2 + j3/(1 - j6)
The conjugate of a complex number a + bj is given by a - bj.
In this case, the conjugate of (1 - j6) is (1 + j6). So, multiplying both the numerator and denominator by (1 + j6), we get:
[(2 + j3) * (1 + j6)] / [(1 - j6) * (1 + j6)]
Expanding the numerator and denominator, we have:
[(2 + j3)(1 + j6)] / [1² - (j6)²]
Simplifying each term within the numerator and denominator, we get:
[(2 + j3)(1 + j6)] / [1 - (-36)]
Continuing to simplify, we have:
[(2 + j3)(1 + j6)] / [1 + 36]
Multiplying the terms within the numerator, we get:
(2 * 1) + (2 * j6) + (j3 * 1) + (j3 * j6) / 37
Simplifying further, we have:
2 + 12j + j3 + j² * 3 / 37
The term j² is equal to -1, so the expression becomes:
2 + 12j + j3 - 3 / 37
Combining like terms, we have:
(2 - 3) + (12 + 3)j / 37
This simplifies to:
-1 + 15j / 37
Therefore, the first complex number (2 + j3/1 - j6) simplifies to -1 + 15j / 37.
Now let's move on to the second complex number, (7 - j8/-5 + j11):
The expression can be rewritten as:
(7 - j8) / (-5 + j11)
To simplify the expression further, we again need to rationalize the denominator. We multiply both the numerator and denominator by the conjugate of the denominator, which in this case is (-5 - j11).
[(7 - j8) * (-5 - j11)] / [(-5 + j11) * (-5 - j11)]
Expanding the numerator and denominator, we get:
[(-35 - 7j11 + j8 * 5 - j8 * j11)] / [(-5)² - (j11)²]
Simplifying each term within the numerator and denominator, we have:
[-35 - 7j11 + 5j8 - j8j11] / [25 - j²11]
Simplifying further, we have:
[-35 - 7j11 + 5j8 + j² * 8 * 11] / [25 - (-121)]
Since j² is equal to -1, the expression becomes:
[-35 - 7j11 + 5j8 - 88] / [25 + 121]
Combining like terms, we have:
(-123 - 7j11 + 5j8) / 146
Therefore, the second complex number (7 - j8/-5 + j11) simplifies to (-123 - 7j11 + 5j8) / 146.
Finally, we can evaluate the sum of the two complex numbers by adding them together:
(-1 + 15j / 37) + ((-123 - 7j11 + 5j8) / 146)
To add these complex numbers, we add the real parts together and the imaginary parts together:
(-1 + -123) + (15j + -7j11 + 5j8) / 37 + 146
Simplifying further, we get:
-124 + 15j - 77j + 40j / 37 + 146
Combining like terms, we have:
-124 - 62j / 37 + 146
The final result of the evaluation is:
22 - (62/37)j
To know more about complex number here
https://brainly.com/question/20566728
#SPJ4
On a particular day, 6 students in a class were absent, which is 20% of the class. What is the total number of students in the class?
Answers
Answer:
30
Step-by-step explanation:
The total number of students in the class is equal to 30 students.
What do you mean by percentage ?
Percentage is the relative value indicating one hundredth part of any quantity.
The number of students who were absent on a particular day is 6 students.
The number of absent students is 20 % of total number of students in the class. We know that percent meant something out of 100. Here , 20 % will be equal to :
= \(\frac{20}{100}\)
Let's assume total number of students in class be x.
To find out the total number of students in the class we need to divide the percent of absent students by number of absent students , that is :
x = 6 ÷ \(\frac{20}{100}\)
We know that if the division symbol is converted to multiplication then , we need to inverse the second term which is left to the division symbol , that is :
x = 6 × \(\frac{100}{20}\)
x = 6 × 5
or
x = 30 students
Therefore , the total number of students in the class is equal to 30 students.
Learn more about percentage here :
https://brainly.com/question/22091903
#SPJ5
How much is 600 divide by 50 + 30 x 100 - 600 divide by 0 don’t use the calculator
Answers
Answer:
The result is 9000.
Step-by-step explanation:
The calculation is done as follows:
600 ÷ 50 = 12
12 + 30 x 100 = 3200
3200 - 600 ÷ 0 = 9000
However, dividing by 0 is undefined and results in an error.