Answers
Answer: Casey bought 4 1/2 pounds of apples
The equation is 0.88x - $1.50 = 2.46
x is the unknown number of pounds of apples.
0.88 is the cost per pound, 0.88x is the total cost of the apples before the discount .The discount is $1.50 $2.46 is the cost after the discount.
Part b Step-by-step explanation:
0.88x - $1.50 = 2.46 . Add $1.50 to both sides
0.88x - $1.50 + $1.50 = 2.46 + 1.50
On left, 1.50-1.50=0 so "cancels' on the right, add $2.46 + 1.50 = 3.96
0.88x = 3.96 is the cost before discount . Divide both sides by .88
.88x/.88 = 3.96/.88 . .88/.88 = 1 so 1 'cancels' leaving x. 3.96/.88 = 4.5
x = 4.5
part c
4.5 is 4 1/2, the (previously unknown) number of pounds of apples.
Casey bought 4 1/2 pounds of apples.
Related Questions
the scores on a collegiate mathematics readiness assessment are approximately normally distributed with a mean of 680 and a standard deviation of 120. determine the percentage of scores between 690 and 900, to the nearest percent.
Answers
43.36% of the scores fall between 690 and 900 on the collegiate mathematics readiness assessment.
To determine the percentage of scores between 690 and 900, we need to calculate the area under the normal distribution curve between these two values.
First, we need to standardize the scores using the formula z = (x - μ) / σ, where x is the score, μ is the mean, and σ is the standard deviation.
For the score 690:
z1 = (690 - 680) / 120 = 0.0833
For the score 900:
z2 = (900 - 680) / 120 = 1.8333
Next, we need to find the area between these two standardized scores. We can use a standard normal distribution table or a statistical calculator to find the corresponding probabilities.
From the standard normal distribution table, we find that the area to the left of z1 is approximately 0.5328 and the area to the left of z2 is approximately 0.9664.
To find the area between z1 and z2, we subtract the smaller area from the larger area:
Area = 0.9664 - 0.5328 = 0.4336
Finally, we convert the area to a percentage by multiplying by 100:
Percentage = 0.4336 * 100 ≈ 43.36%
Therefore, approximately 43% of the scores fall between 690 and 900 on the collegiate mathematics readiness assessment.
Know more about percentage here:
https://brainly.com/question/24877689
#SPJ8
please help me i dont know the answer to both of these.

Answers
Answer:
The answer for the first one is D: Multiply x by 5 and 2 by 5.
The answer for the second one is: A: There are infinitely many solutions.
Step-by-step explanation:
I am doing Linear equations right now in school lol
D, multiply x by 5 and 2 by 5
The second answer is
A, there are infinite amounts of solutions
Find the volume of the following solid using triple integrals. The wedge of the cylinder x² + 4y² = 4 created by the planes z = 1 - x and z = x - 1.
The volume of the given solid is ...
Answers
The volume of the given solid is 4/3 cubic units.
To find the volume of the given solid using triple integrals, we can set up the integral in the following way:
V = ∭E dz dy dx
Where E represents the region enclosed by the cylinder x² + 4y² = 4 and the planes z = 1 - x and z = x - 1.
To set up the integral limits, we first need to find the intersection points of the cylinder and the planes. Solving for x in the cylinder equation, we get:
x² + 4y² = 4
x² = 4 - 4y²
x = ±√(4 - 4y²)
Substituting these values of x into the equations of the planes, we get:
z = 1 - x: z = 1 ± √(4 - 4y²)
z = x - 1: z = ±√(4 - 4y²) - 1
Since the solid is symmetric about the yz-plane, we can integrate over the right half of the solid and multiply by 2 to get the total volume. So we can set up the integral limits as follows:
0 ≤ x ≤ √2
0 ≤ y ≤ 1/2 * √(4 - x²/4)
1 - x ≤ z ≤ √(4 - 4y²) - 1
Then the volume can be calculated as:
V = 2 ∭E dzdydx
V = 2 ∫₀^(√2) ∫₀^(1/2 * √(4 - x²/4)) ∫^(√(4 - 4y²) - 1)_(1 - x) dzdydx
Evaluating this integral using appropriate techniques, we get:
V = 4/3
Therefore, the volume of the given solid is 4/3 cubic units.
To learn more about the integrals visit: brainly.com/question/30376753
#SPJ11
∠1 and ∠2 are complementary angles. m∠1 is 5y+32 and m∠2 is 7y-14. Find m∠2 & show your work.
it was deleted last time I posted it???
Answers
\(\\ \sf\longmapsto 5y+32+7y-14=90\)
\(\\ \sf\longmapsto 12y+18=90\)
\(\\ \sf\longmapsto 12y=72\)
\(\\ \sf\longmapsto y=6\)
m<2=7(6)-14=42-14=28\)The required value of m∠2 would be 30 degrees when the value of y = 6 due to the given pair of angles being complementary.
What are complementary angles?The complementary angles are defined as when pairing of angles addition to 90° then they are called complementary angles.
We have been given that the pair of angles as
(5y + 32)° and (7y - 14)°
∵ ∠1 and ∠2 are complementary angles
Here, the pairing of angles sums up to 90° then they are called complementary angles.
So 5y + 32 + 7y - 14 = 90°
⇒ 12y + 18 = 90
⇒ 12y = 72
⇒ y = 6
So m∠2 = 7y - 14
Substitute the value of y = 6 in the above equation, and we get
So m∠2 = 7(6) - 14 = 42 -12 = 30
Therefore, the value of m∠2 would be 30 degrees when the value of y = 6.
Learn more about the complementary angles here:
brainly.com/question/5708372
#SPJ5
A chef divides 5 heads of lettuce equally among 12 salad plates. How much lettuce will be on each plate?
Answers
Answer:
It is ...
Step-by-step explanation:
The required fraction at which lettuce will be divided in is 5/12.
What is simplification?The process in mathematics to operate and interpret the function to make the function or expression simple or more understandable is called simplifying and the process is called simplification.
What is the Ratio?The ratio can be defined as the proportion of the fraction of one quantity towards others. e.g.- water in milk.
here,
A chef divides 5 heads of lettuce equally among 12 salad plates. ,
The ratio in which 5 heads of lettuce will be divided in 12 plates is given as,
= 5 / 12
Thus, the required fraction at which lettuce will be divided in is 5/12.
Learn more about ratios here:
brainly.com/question/13419413
#SPJ2
Joshua has a gold (AU) nugget with a mass of 25 grams. If the density of gold is 19.32 g/cm3.
How much space would the nugget take up in a graduated cylinder?"
a).77 ml
b)483 ml
c)1.29 ml
d)44.32 ml
Answers
Set up a system of equations for the given information by filling in the boxes with the coefficients of the variables and the constant values, where is the amount invested in stocks, is the amount invested in bonds, and is the amount invested in CD's.
If there is no visible coefficient, then enter
for the coefficient.
If a specific variable is not present in the equation, then enter
for the coefficient.
Country Day's scholarship fund receives a gift of $200000. The money is invested in stocks, bonds, and CDs. CDs pay 5% interest, bonds pay 2.9% interest, and stocks pay 10.9% interest. Country day invests $20000 more in bonds than in CDs. The total amount earned from the investments is $11165.
Total amount invested:
+ +
=
Total amount earned from investements:
+ +
=
Relation of bonds and CDs:
+ + =
Answers
Answer: Total amount invested:
= 200000
Total amount earned from investements:
0.109x + 0.029y + 0.05z = 11165
Relation of bonds and CDs:
= +20000
Step-by-step explanation:
Line segment AC is given by (-4, -3) and C (6,4).
Find the coordinates of point B such that AB:BC is 3:2.
Answers
Answer:
Step-by-step explanation:
3/(3+2) = 3/5
B is 3/5 of the distance from A to C.
Interpolate the coordinates of B:
Difference of x-coordinates = 6-(-4) = 10
3/5 of 10 = 6
x-coordinate of B = (x-coordinate of A) + 6 = -4 + 6 = 2
Difference of y-coordinates = 4-(-3) = 7
3/5 of 7 = 21/5
y-coordinate of B = (y-coordinate of A) + 21/5 = 6/5
B(2, 6/5)
For any 2 points , there is a unique _____ through them .
A) Point
B) Line
C) Plane
D) Intersection
Answers
B) Line
I hope this helps!!!
let p and q be distinct primes. (1) prove that (z/(pq))× has order (p − 1)(q − 1);
Answers
The order of a in (z/(pq))× is exactly (p-1)(q-1), as desired.
To prove that (z/(pq))× has order (p − 1)(q − 1), we need to show that the least positive integer n such that (z/(pq))×n = 1 is (p − 1)(q − 1).
First, let's define (z/(pq))× as the set of all integers a such that gcd(a,pq) = 1 (i.e., a is relatively prime to pq) and a mod pq is also relatively prime to pq.
Now, we know that the order of an element a in a group is the smallest positive integer n such that a^n = 1. Therefore, we need to find the order of an arbitrary element a in (z/(pq))×.
Let's assume that a is an arbitrary element in (z/(pq))×. Since gcd(a,pq) = 1, we know that a has a multiplicative inverse modulo pq, denoted by a^-1. Therefore, we can write:
a * a^-1 ≡ 1 (mod pq)
Now, let's consider the order of a. Since gcd(a,pq) = 1, we know that a^(p-1) is congruent to 1 modulo p by Fermat's Little Theorem. Similarly, we can show that a^(q-1) is congruent to 1 modulo q. Therefore, we have:
a^(p-1) ≡ 1 (mod p)
a^(q-1) ≡ 1 (mod q)
Now, we can use the Chinese Remainder Theorem to combine these congruences and get:
a^(p-1)(q-1) ≡ 1 (mod pq)
Therefore, we know that the order of a must divide (p-1)(q-1).
To show that the order of a is exactly (p-1)(q-1), we need to show that a^k is not congruent to 1 modulo pq for any positive integer k such that 1 ≤ k < (p-1)(q-1).
Assume for contradiction that there exists such a k. Then, we have:
a^k ≡ 1 (mod pq)
This means that a^k is a multiple of pq, which implies that gcd(a^k, pq) ≥ pq. However, since gcd(a,pq) = 1, we know that gcd(a^k, pq) = gcd(a,pq)^k = 1. This is a contradiction, and therefore our assumption must be false.
Know more about prime here:
https://brainly.com/question/20532807
#SPJ11
The order of a in (z/(pq))× is exactly (p-1)(q-1), as desired.
To prove that (z/(pq))× has order (p − 1)(q − 1), we need to show that the least positive integer n such that (z/(pq))×n = 1 is (p − 1)(q − 1).
First, let's define (z/(pq))× as the set of all integers a such that gcd(a,pq) = 1 (i.e., a is relatively prime to pq) and a mod pq is also relatively prime to pq.
Now, we know that the order of an element a in a group is the smallest positive integer n such that a^n = 1. Therefore, we need to find the order of an arbitrary element a in (z/(pq))×.
Let's assume that a is an arbitrary element in (z/(pq))×. Since gcd(a,pq) = 1, we know that a has a multiplicative inverse modulo pq, denoted by a^-1. Therefore, we can write:
a * a^-1 ≡ 1 (mod pq)
Now, let's consider the order of a. Since gcd(a,pq) = 1, we know that a^(p-1) is congruent to 1 modulo p by Fermat's Little Theorem. Similarly, we can show that a^(q-1) is congruent to 1 modulo q. Therefore, we have:
a^(p-1) ≡ 1 (mod p)
a^(q-1) ≡ 1 (mod q)
Now, we can use the Chinese Remainder Theorem to combine these congruences and get:
a^(p-1)(q-1) ≡ 1 (mod pq)
Therefore, we know that the order of a must divide (p-1)(q-1).
To show that the order of a is exactly (p-1)(q-1), we need to show that a^k is not congruent to 1 modulo pq for any positive integer k such that 1 ≤ k < (p-1)(q-1).
Assume for contradiction that there exists such a k. Then, we have:
a^k ≡ 1 (mod pq)
This means that a^k is a multiple of pq, which implies that gcd(a^k, pq) ≥ pq. However, since gcd(a,pq) = 1, we know that gcd(a^k, pq) = gcd(a,pq)^k = 1. This is a contradiction, and therefore our assumption must be false.
Know more about prime here:
https://brainly.com/question/20532807
#SPJ11
Solve and check the following equation. −75 = −5d − 150d =
Answers
Answer:
15/31 is the answer.
Step-by-step explanation:
-75 = -5d- 150d
-5d- 150d= - 155d
divide -75 from -155d
-155d / -155= -75 / -155
=15 / 31
-75 = -155d
-75/-155 = d
15/31 = d
!!!!!!!!
What is the coefficient of the second term of the expression 3x^4 + x^2?

Answers
Answer:
1
Step-by-step explanation:
because no number Is beside it except 1 because 1 x anything will give it back
The coefficient of the second term of the expression 3x⁴ + x² will be 1. Then the correct option is B.
What is a polynomial?A polynomial expression is an algebraic expression with variables and coefficients. Unknown variables are what they're termed. We can use addition, subtraction, and other mathematical operations. However, a variable is not divisible.
The expression is given below.
⇒ 3x⁴ + x²
The number which is associated with the variable is known as the coefficient of that variable.
In the expression 3x⁴ + x², the coefficient of x⁴ is 3 and the coefficient of x² is 1.
The coefficient of the second term of the expression 3x⁴ + x² will be 1. Then the correct option is B.
More about the polynomial link is given below.
https://brainly.com/question/17822016
#SPJ5
State GCF of following monomials 18m5n4 and 45m3n6
Answers
Answer:
9m³n⁴
Step-by-step explanation:
18m^5n^4 = 2×3² m^5n^4
45m^3n^6 = 3²×5 m^3n^6
GFC = 3² m³n⁴ = 9m³n⁴
A function has the points (1,5), (3,6), (4, 10), and (2, y).
Which point, (2, y), would keep this a function?
(4,11)
(4,5)
(3,8)
(6,3)
Answers
Answer:
sorry I don't know the answer
Use the method of cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the curves y=x2, y=0, x=1, and x=2 about the line x=4.
Answers
Volume of the solid obtained by rotating the region is 67π/6 .
Given,
Curves:
y=x², y=0, x=1, and x=2 .
The arc of the parabola runs from (1,1) to (2,4) with vertical lines from those points to the x-axis. Rotated around x=4 gives a solid with a missing circular center.
The height of the rectangle is determined by the function, which is x² . The base of the rectangle is the circumference of the circular object that it was wrapped around.
Circumference = 2πr
At first, the distance is from x=1 to x=4, so r=3.
It will diminish until x=2, when r=2.
For any given value of x from 1 to 2, the radius will be 4-x
The circumference at any given value of x,
= 2 * π * (4-x)
The area of the rectangular region is base x height,
= \(\int _1^22\pi \left(4-x\right)x^2dx\)
= \(2\pi \cdot \int _1^2\left(4-x\right)x^2dx\)
= \(2\pi \left(\int _1^24x^2dx-\int _1^2x^3dx\right)\)
= \(2\pi \left(\frac{28}{3}-\frac{15}{4}\right)\)
Therefore volume of the solid is,
= 67π/6
Know more about volume of solids,
https://brainly.com/question/23705404
#SPJ4
Factor completely: 5x^2-11x+6
Answers
Answer^^^^
can some one help me i dont understand what this is telling me to do
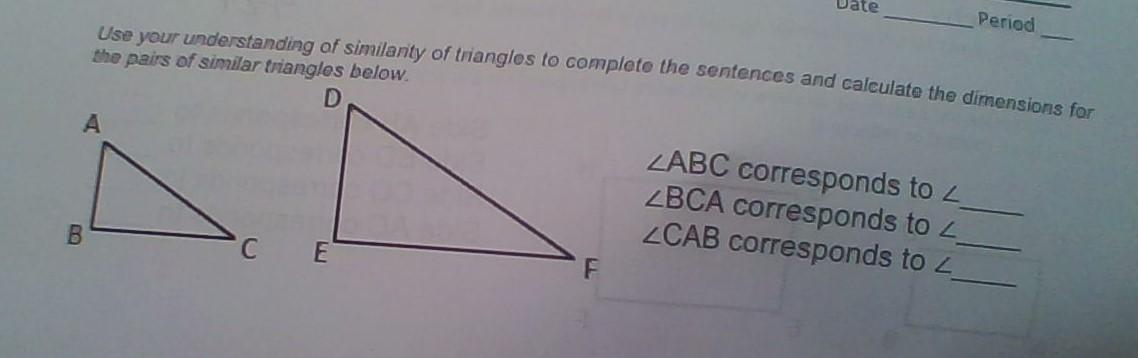
Answers
Answer:
ABC corresponds to DEF
BCA corresponds to EFD
CAB corresponds to FDE
Step-by-step explanation:
The questions is asking you to find where the point on the small triangle are on the larger triangle, so if it said something like B corresponds to __, your answer would be E. This one just ask for three in a row, so do the points in order. That is all you have to do!
Answer: ABC correspond to DEF. BCA coressponds to EFD. CAB corresponds to FED
Step-by-step explanation:
Its telling you what letters coordinate with what letters for example ; FDE corresponds to CAB
a.) If m 1 = 3x - 7, find x.

Answers
Answer:
x = 25
Step-by-step explanation:
Angle 1 and the angle opposite from Angle 1 (the angle that's 68°) are vertical angles.
What are vertical angles, you ask?
According to the Oxford dictionary, vertical angles are each of the pairs of opposite angles made by two intersecting lines.
For example, take the letter X. The letter X has two lines that intersect to form 4 angles. The top and bottom angles are a pair of vertical angles. So are the left and right angles.
Vertical angles are always congruent.
(This is VERY important to know! It will help you solve many types of geometry problems!)
m1 is 3x - 7. Because Angle 1 and the angle that's 68° are vertical angles, that means they are equal to each other.
Therefore: 3x - 7 = 68.
Now, you can solve for x to get x = 25.
Hope this helps!
Bob bought 40 gumboils from a quarter machine. The number of each flavor he got is shown in the table. If there are 140 gumboils remaining in the machine, what is a reasonable prediction for the number of cola flavored gumboils left?
Flavors: Amount:
Grape 4
Cherry 12
Cola 16
Orange 8
Answers
Answer:
56 cola flavored gumboils
Step-by-step explanation:
Bob's 40 count of gumballs has 16 cola gumballs
Therefore the probability of a gumball being cola based on the sample size of Bob's purchase = 16/40 = 2/5
There are 140 gumballs left in the machine so we can expect that, on an average, 2/5 of them should be cola gumballs
So number of cola gumballs left is expected to be 2/5 x 140 = 56
This is only a prediction based on Bob's sample of 40 cola gumballs
Given the system of equations: 5x + 2y = 3 4x − 8y = 12 solve for (x, y) using elimination. a. (−7, 5) b. (−5, −4) c. (1, −1) d. (3, −6)
Answers
Answer:
c. (1,-1)
Step-by-step explanation:
5x + 2y = 3 4x – 8y = 12 Solve for (x, y)
4x-8y=12
+8y +8y
4x=12+8y
Divide both sides by 4
4x/4=(12+8y)/4
x=3+2y
Then take x equation and input into 5x + 2y = 3
5(3+2y)+2y=3
15+10y+2y=3
Add 10y and 2y
15+12y=3
Subtract 15 on both sides
15-15+12y=3-15
12y=-12
Divide 12 both sides
12y÷12=-12÷12
Y = -1
Insert the Y equation into 4x – 8y = 12
4x-8(-1)=12
4x+8=12
Subtract 8 on both sides
4x-8-8=12-8
4x=4
Divide 4 both sides
4x÷4=4÷4
X = 1
Answer: C. (1, -1)
with the new dough, there were 16 complaints out of 340 pizzas. let p1 be the proportion of customer complaints with the old dough and p2 be the proportion of customer complains with the new dough. based on a 95% confidence for the difference of the proportions, what can be concluded?
Answers
The correct answer is:
Reject null hypothesis H0, we cannot conclude the proportion of customer complaints is more for the old dough.
As given in the question,
Let us consider proportion of customer complaints with old dough is p₁
And proportion of complaints with new dough is p₂
Difference in proportion of complaints in old and new dough
= p₁ - p₂
Null hypothesis : H0 : p1 ≥ p2
p₁ - p₂ ≥ 0
Alternative hypothesis : Ha : p1 < p2
p1 - p2 < 0
Let 'x' represents the number of complaints
Sample size = n
Sample proportion = x/n
Old dough:
Number of complains with old dough 'x₁' = 6
Number of pizzas with old dough 'n₁' = 385
p₁ = 6/385
= 0.01558
= 0.016
New dough:
Number of complains with new dough 'x₂' = 16
Number of pizzas with new dough 'n₂' = 340
p₂ = 16/340
= 0.04705
= 0.047
Pooled proportion test:
\(\bar{p}\) = (x₁+ x₂)/(n₁ + n₂)
= (6 + 16)/(385 + 340)
= 0.0303
= 0.03
1 - \(\bar{p}\) = 1 - 0.03
= 0.97
z = (p₁ - p₂)/√\(\bar{p}\)(1 - \(\bar{p}\))(1/n₁ + 1/n₂)
= (0.016 - 0.047)/√(0.03)(0.97)(1/385 + 1/340)
= (-0.031)/ √(0.03)(0.97)(0.0026 + 0.0029)
= - 0.031/√0.00016005
= -0.031 / .01265
= -2.45
It is left tailed test.
p value for the area to the left of the z score using normal distribution table:
p value = 0.007143
Significant level 'α' for 95% confidence level:
= 1 - 0.95
= 0.05
Since 0.05 > 0.0.007143
Reject null hypothesis.
Therefore, reject H0, we cannot conclude the proportion of customer complaints is more for the old dough.
The complete question is :
Paul owns a mobile wood-fired pizza oven operation. A couple of his clients complained about his dough at a recent catering, so he changed his dough to a newer product. Using the old dough, there were 6 complaints out of 385 pizzas. With the new dough, there were 16 complaints out of 340 pizzas. Let p1 be the proportion of customer complaints with the old dough and p2 be the proportion of customer complains with the new dough. Based on a 95% confidence for the difference of the proportions, what can be concluded?
Multiple Choice
A. Reject H0, we can conclude the proportion of customer complaints is more for the old dough
B. Do not reject H0, we cannot conclude the proportion of customer complaints is more for the old dough
C. Do not reject H0, we can conclude the proportion of customer complaints is more for the old dough
D. Reject H0, we cannot conclude the proportion of customer complaints is more for the old dough
Learn more proportion here
brainly.com/question/7096655
#SPJ4
what is the answer to this equation? x^2-18x+206=0
Answers
x = 9-5^(3/2)*i or x = 5^(3/2)*i+9
ok done. Thank to me :>
solve this problem pls

Answers
The simplified form of the given expression is 8.5.
What is simplification?In arithmetic, the operation and interpretation of a function to make it simpler or easier to grasp is known as simplifying, and the process itself is known as simplification.
The expression is given in the question, as follows:
11 1/2 - (3 1/3 + 2 2/5)(1 - 28/43)
Convert the mixed numbers into fractions:
23/2 - (10/3 + 12/5)(1 - 28/43)
Taking LCM and solving the expression to get:
23/2 - (86/15)(15/43)
23/2 - 2
19/2
8.5
Thus, the solution to the given expression is 8.5.
Learn more about Expressions here:
brainly.com/question/13947055
#SPJ2
Seven friends each bought a movie ticket for $14.95, popcorn for $6.99, and a drink for $2.25. How much did the friends spend in all?
Answers
Answer:
$169.33
Step-by-step explanation:
Each of the friends spent ...
$14.95 +6.99 +2.25 = $24.19
The seven friends together spent ...
7($24.19) = $169.33
Use Newton's method to approximate the zero of the function f(x)=x^3-4x+33 to five decimal places. Round any intermediate calculations, if needed, to no less
than six decimal places, and round your final answer to five decimal places.
Answers
can a triangle have sides with the given lengths? Explain 1ft,2 ft ,5 ft

Answers
No, because 1 + 2 < 5 contradicts the triangle inequality therem (option C)
Explanation:
The triangle inequality theorem states that the sum of any two sides of a triangle must be greater than the length of the third side.
Given the 3 sides as: 1ft, 2 ft, 5 ft
Using the triangle inequality:
1 + 2 > 5
3 > 5 (this is false)
1 + 5 > 2
6 > 2 (this is true)
2 + 5 > 1
7 > 1 (this is true)
There is something else about the theorem, the sum of the two shorter sides should be greater than the sum of the longest side.
In our solution 1+2 > 5 which is false.
Hence, it is not possible to have a triangle with sides 1ft, 2ft and 5 ft because 1 + 2 < 5
The correct option: No, because 1 + 2 < 5 contradicts the triangle inequality therem (option C)
Shopping at savers mart, Lisa buys her children four shirts and three pairs of pants for $85.50. She returns the next day and buys three shirts and five pairs of pants for $115.00. What is the price of each shirt and each pair of pants?
Answers
The price of each shirt is $7.5.
The price of each pant is $18.5.
What is an equation?An equation is a mathematical statement that is made up of two expressions connected by an equal sign.
Example:
2x + 3 = 7 is an equation.
We have,
Cost of shirts = x
Cost of pants = y
Lisa buys her children four shirts and three pairs of pants for $85.50.
She returns the next day and buys three shirts and five pairs of pants for $115.00.
This means,
We can make two equations.
4x + 3y = 85.50
3x + 5y = 115
Now,
4x + 3y = 85.50
4x = 85.50 - 3y
x = (85.50 - 3y)/4
Substituting in 3x + 5y = 115.
3 (85.50 - 3y)/4 + 5y = 115
256.5 - 9y + 20y = 460
11y = 460 - 256.6
11y = 203.4
y = 18.5
And,
x = (85.50 - 3y)/4
x = (85.50 - 55.5)/4
x = 30/4
x = 7.5
Thus,
The cost of the shirt is $7.5.
The cost of the pant is $18.5.
Learn more about equations here:
https://brainly.com/question/17194269
#SPJ1
what is the quotient? x2-10x+25/(x-5)(x+5)

Answers
Answer:-2.3,11.,11.,-0.25 or x2 - 10x - 25- -5
Step-by-step explanation:
u just go in a TI-nspire CX calculator and type in in how it looks
Celine surveyed 14 students at her school about their favorite professional sports. Of the students surveyed, 6 said tennis was their favorite sport. What is the experimental probability that the next student Celine talks to will pick tennis?
Answers
Answer:
3/7 (simplified)
Step-by-step explanation:
The original answer would be 6/14 because 6 out of 14 people said tennis. However, you divide both by 2 to get 3/7. The percent would be 42% if that is needed.
Find the area of each

Answers
Answer:
176/77 is the answer I think so
Answer:
look at the picture I sent

