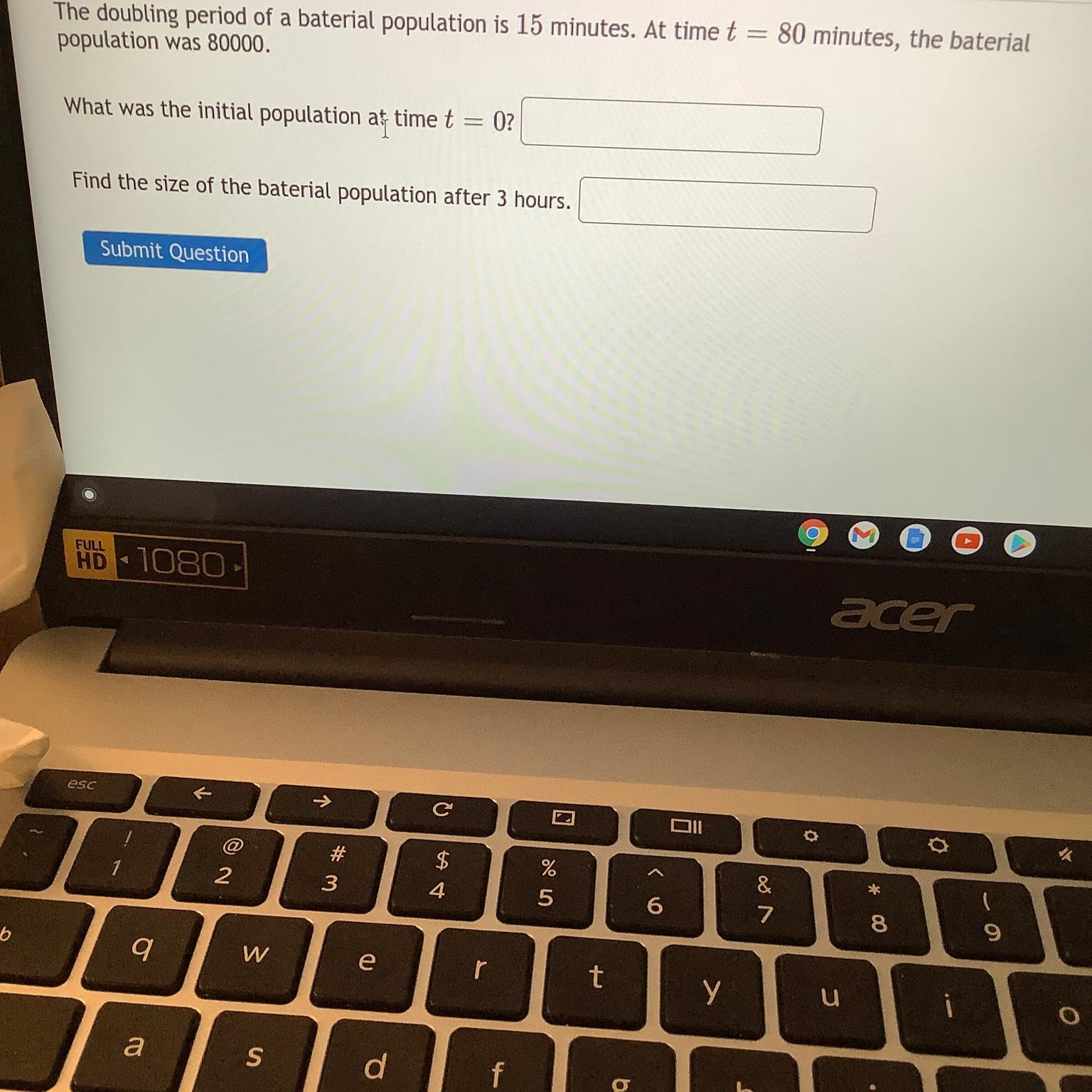
Answers
The exponential function involving doubling period is expressed as
P = Po(2)^t/T
where
Po is the initial or starting value
t is the time of growth
T is the doubing time
t/T is the ratio describing the number of doubings over time t
From the information given,
T = 15
t = 80
P = 80000
We want to find Po
We have
80000 = Po(2)^80/15
80000 = 40.32Po
Po = 80000/40.32 = 1984
The initial population is 1984
Thus, the function is
P = 1984(2)^t/15
For 3 hours, recall,
1 hour = 60 minutes
3 hours = 3 * 60 = 180 minutes
We would substitute t = 180 into the equation. We have
P = 1984(2)^180/15 = 1984(2)^12
P = 8126464
The size of the bacterial population after 3 hours is 8126464
Related Questions
Point-slope equation
y-6=3(x - 5)
y- 4 = -9(x+8)
y- 2 = 5x
Slope
-10
2
712
2
Point on
line
(1,4)
(5,-3)
(-7,-7)

Answers
The point slope equation and slope of some lines are given below
1) For y - 6 = 3(x - 5), slope = 3
2) For y - 4 = -9(x + 8), slope = -9
3) y - 2 = 5x, slope = 5
4) Point slope equation of line whose slope = -10 and passing through (1, 4)
y - 4 = -10(x - 1)
5) Point slope equation of line whose slope = 2 and passing through (5, -3)
y + 3 = 2(x - 5)
6) Point slope equation of line whose slope = \(\frac{1}{2}\) and passing through (-7, -7)
\(y +7 = \frac{1}{2}(x +7)\\\)
What is equation of line in point slope form?
The most general form of equation of line in point slope form is given by \(y - y_1 = m(x - x_1)\) , \((x_1, y_1)\) is a point on the line
Where m is the slope of the line
Slope of a line is the tangent of the angle that the line makes with the positive direction of x axis.
If \(\theta\) is the angle that the line makes with the positive direction of x axis, then slope (m) is given by
m = \(tan\theta\)
1) y - 6 = 3(x - 5)
y - 6 = 3x - 15
y = 3x - 15 + 6
y = 3x - 9
Slope = 3
If x = 0,
\(y = 3 \times 0 -9\\y = -9\)
(0, -9) is a point on the line
2) y - 4 = -9(x + 8)
y - 4 = -9x - 72
y = -9x - 72 + 4
y = -9x - 68
Slope = -9
If x = 0
\(y = -9 \times 0 -68\\y = -68\)
(0, -68) is a point on the line
3) y - 2 = 5x
y = 5x + 2
Slope = 5
Putting x = 0
\(y = 5 \times 0 + 2\\y = 2\)
(0, 2) is a point on the line
4) Slope = - 10
The line passes through (1, 4)
Point slope equation
y - 4 = -10(x - 1)
5) Slope = 2
The line passes through (5, -3)
Point slope equation
y - (-3) = 2(x - 5)
y + 3 = 2(x - 5)
6) Slope = \(\frac{1}{2}\)
The line passes through (5, -3)
Point slope equation
\(y - (-7) = \frac{1}{2}(x - (-7))\\y +7 = \frac{1}{2}(x +7)\\\)
To learn more about point slope equation and slope, refer to the link-
https://brainly.com/question/24907633
#SPJ9
A normally distributed data set has a mean of 0 and a standard deviation of 0.5. Which is closest to the percent of values between –1 and 1?
34%
50%
68%
95%
Answers
As a result, 68% of the data falls into the range of values between -1 and 1, which is one standard deviation from the mean. The closest estimate of the solution is 68%.
What is equation?A mathematical equation is a formula that connects two claims and uses the equals symbol (=) to denote equivalence. An equation in algebra is a mathematical statement that establishes the equivalence of two mathematical expressions. For instance, in the equation 3x + 5 = 14, the equal sign places a space between the variables 3x + 5 and 14. The relationship between the two sentences that are written on each side of a letter may be understood using a mathematical formula. The symbol and the single variable are frequently the same. as in, 2x - 4 equals 2, for instance.
For a normally distributed data set with a mean of 0 and a standard deviation of 0.5, the proportion of values between -1 and 1 is most closely related to 68%.
Approximately 68% of the data in a normal distribution lies within one standard deviation of the mean, which explains why. One standard deviation below the mean is -0.5, and one standard deviation above the mean is 0.5 since the mean is 0 and the standard deviation is 0.5. As a result, 68% of the data falls into the range of values between -1 and 1, which is one standard deviation from the mean. The closest estimate of the solution is 68%.
To know more about equation visit:
https://brainly.com/question/649785
#SPJ1
What's the Unit Rate? please. :')

Answers
Answer:
The unit rate is 8.
Step-by-step explanation:
(5, 40) = 8
(10, 80) = 8
(15, 120) = 8
you can simply divide and find the unit rate.
Find the perimeter of the figure to the right
6 yards
8 4/5 yard
9 2/3 yards
8 yards
Answers
what is the equation of a line that passes through the points (2,5) and (4,3)
Answers
The equation of a line that passes through points (2,5) and (4,3) is
y = -x+7.
Finding the equation of a line:
First, we need to find out the slope for the given points.
(X1,Y1) = (2,5)
(X2,Y2) = (4,3)
formula for slope(m) = \(\frac{Y2 - Y1}{X2 - X1}\)
substitute the points in the above formula
\(\frac{3 - 5}{4 - 2}\) = \(\frac{-2}{2}\)
\(\frac{-2}{2}\) = -1
slope for the given points(m) = -1.
m = -1
The equation of a line is y-y1 = m(x-x1), where x and y are variables.
substituting the values in the above equation then :
y-5 = -1(x-2)
y-5 = -x+2
y+x = 2+5
x+y = 7
y = -x+7
Therefore, the equation of the line passing through the points (2,5) and (4,3) is y = -x+7
To solve more problems based on the linear equations:
https://brainly.com/question/9753782
which best describes how to solve the equations below 35x=88
Answers
Which of the following is equivalent to the expression below?

Answers
Answer:
A is true
Step-by-step explanation:
PLEASE MARK ME BRAINLIEST IF MY ANSWER IS CORRECT PLEASE
\(\textbf {Allow me to assist you.}\)
\(\textrm {Let's simplify the terms under the radicals.}\)
\(\mathsf {\sqrt{8} - \sqrt{72} + \sqrt{50}}\)
\(\mathsf {\sqrt{2 \times 2^{2}} - \sqrt{2 \times 6^{2}} + \sqrt{2 \times 5^{2}}}\)
\(\mathsf {2\sqrt{2} - 6\sqrt{2} + 5\sqrt{2}}\)
\(\boxed {\sqrt{2}}\)
\(\textbf {The answer is A.}\)
Describe how the volume of a triangular prism and a triangular pyramid with the same dimensions are related.
Answers
Answer:
The relationship between the volumes of pyramids and prisms is that when a prism and pyramid have the same base and height, the volume of the pyramid is 1/3 of the volume of the prism.
Hope this helps!! ;)
volume of the prism is three times the volume of the pyramid with the same dimensions.
What is the volume?Volume is the measure of the capacity that an object holds.
Formula to find the volume of the object is Volume = Area of a base × Height.
Volume of a triangular prism = area of base triangle × length of the prism
The volume of a triangular pyramid = (1/3) × Base Area × Height
The relationship between a triangular prism and a triangular pyramid with equal bases and heights is that the volume of the prism is three times the volume of the pyramid.
Therefore, volume of the prism is three times the volume of the pyramid with the same dimensions.
To learn more about the volume visit:
https://brainly.com/question/13338592.
#SPJ2
To make a big batch of cookies for her father, Annmarie needs 1 1/4 pounds of chocolate chips, 3/4 pounds of walnuts, and 12 ounces of raisins. How many ounces of these three ingredients does she need in all?
A. 28ounces
B. 44ounces
C. 48ounces
D. 76ounces
Answers
Answer: B. 44 ounces
Answer:
what was it ??
Step-by-step explanation: i taking the test
test test test test test test test test test test
2. (7 points) If f(x) = -5 cosx+xtanx, find df and evaluate if x = pi/4 and dx = 1/24
Answers
The value of df, when x = π/4 and dx = 1/24, is (-5π - 5√2)/(96√2).
To find the derivative of the function f(x) = -5cos(x) + xtan(x), we'll use the sum and product rules of differentiation. Let's start by finding df/dx.
Apply the product rule:
Let u(x) = -5cos(x) and v(x) = xtan(x).
Then, the product rule states that (uv)' = u'v + uv'.
Derivative of u(x):
u'(x) = d/dx[-5cos(x)] = -5 * d/dx[cos(x)] = 5sin(x) [Using the chain rule]
Derivative of v(x):
v'(x) = d/dx[xtan(x)] = x * d/dx[tan(x)] + tan(x) * d/dx[x] [Using the product rule]
= x * sec^2(x) + tan(x) [Using the derivative of tan(x) = sec^2(x)]
Applying the product rule:
(uv)' = (5sin(x))(xtan(x)) + (-5cos(x))(x * sec^2(x) + tan(x))
= 5xsin(x)tan(x) - 5xcos(x)sec^2(x) - 5cos(x)tan(x)
Simplify the expression:
df/dx = 5xsin(x)tan(x) - 5xcos(x)sec^2(x) - 5cos(x)tan(x)
Now, we need to evaluate df/dx at x = π/4 and dx = 1/24.
Substitute x = π/4 into the derivative expression:
df/dx = 5(π/4)sin(π/4)tan(π/4) - 5(π/4)cos(π/4)sec^2(π/4) - 5cos(π/4)tan(π/4)
Simplify the trigonometric values:
sin(π/4) = cos(π/4) = 1/√2
tan(π/4) = 1
sec(π/4) = √2
Substituting these values:
df/dx = 5(π/4)(1/√2)(1)(1) - 5(π/4)(1/√2)(√2)^2 - 5(1/√2)(1)
Simplifying further:
df/dx = 5(π/4)(1/√2) - 5(π/4)(1/√2)(2) - 5(1/√2)
= (5π/4√2) - (10π/4√2) - (5/√2)
= (5π - 10π - 5√2)/(4√2)
= (-5π - 5√2)/(4√2)
= (-5π - 5√2)/(4√2)
Now, to evaluate df/dx when dx = 1/24, we'll multiply the derivative by the given value:
df = (-5π - 5√2)/(4√2) * (1/24)
= (-5π - 5√2)/(96√2)
for such more question on derivative
https://brainly.com/question/23819325
#SPJ8
Suppose A is a 3 x3 matrix and b is a vector in R3 with the property what Ax- b has a unique solution. Explain why the columns of A must span R3 Choose the correct answer below. O A. The equation has a unique solution so for each pair of vectors x and b there is only one possible matrix A. Therefore the columns of A must span R3 O B. The reduced echelon form of A must have a pivot in each row or there would be more than one possible solution for the equation Ax-b. Therefore the columns of A must span R3 O C. Matrix A is a square matrix, so when computing Ax, the row-vector rule shows that the columns of A must span IR3 D When b is written as a linear combination of the columns of A it simplifies to the vector of weights x Therefore the columns of A must span R3
Answers
The correct answer is B. The reduced echelon form of A must have a pivot in each row or there would be more than one possible solution for the equation Ax = b. Therefore, the columns of A must span R3.
For a system of linear equations represented by the matrix equation Ax = b to have a unique solution, the matrix A must have full rank, meaning that the columns of A must span the entire three-dimensional space R3. If the columns of A do not span R3, then there will be more than one solution, which means that the solution is not unique.
In the reduced echelon form of a matrix, each row has a pivot in a unique column. If there is a pivot in every row, this means that the columns of the matrix are linearly independent, which implies that the columns span the entire space. Therefore, in order for the equation Ax = b to have a unique solution, the columns of A must span R3.
The correct answer is B. The reduced echelon form of A must have a pivot in each row or there would be more than one possible solution for the equation Ax = b. Therefore, the columns of A must span R3.
To learn more about echelon form:
https://brainly.com/question/14693506
#SPJ4
Find the graph and all the characteristics (centre,vertex,covertice,length of
minor and major axis,length of latus rectum, equation of directrices and latus
rectum) of the graph with equation 8x^2 + 3y^2 = 24.
Answers
8x²+3y²=24
8x²+3y²-24=0
Let x be 1 ,
Therefore
8+3y²-24=0
3y²-16=0
3y²=16
y²=16/3
y=4/1.7
y=40/17
Take different values of x &y and plot a graph!!!
An ellipse is defined as the path traced by a point as it moves such that the sum of distance from two fixed location is a constant
i) The center of the ellipse, is (0, 0)
ii) The vertex of the ellipse are (-√3, 0), and (√3, 0)
iii) Covertex coordinates are (0, 2·√2), and (0, -2·√2)
iv) Length of the minor axis is 2·√3
v) Length of the major axis is 4·√2
vi) Length of the latus rectum is \(\underline {\dfrac{3 \cdot \sqrt{2} }{2}}\)
vii) The equation of the directrix, is x = ± 8·√5/5
viii) The equation of the latus rectum = √5
The reason the above values are correct are as follows:
The given equation is presented as follows;
8·x² + 3·y² = 24
Required:
To find the center, vertex, covertex, length of minor axis, length of latus rectum, equation of directrices and latus rectum
Solution;
i) The general form of the equation of an ellipse is presented as follows;
\(\dfrac{(x- h)^2}{a^2} + \dfrac{(y - k)^2}{b^2} = 1\)
From the given equation, we get;
The center of the
\(\dfrac{8\cdot x^2}{24} + \dfrac{3\cdot y^2}{24} =\dfrac{x^2}{3} + \dfrac{y^2}{8} = 1\)
The equation of the given ellipse, is \(\dfrac{x^2}{3} + \dfrac{y^2}{8} = 1\)
∴ a = √3, b = 2·√2
The value of h, and k, are both 0
Therefore, the center of the ellipse, (h, k) = (0, 0)
ii) The vertex are (h - a, k), and (h + a, k), which gives;
The vertex are (0 - √3, 0), and (0 + √3, 0)
The vertex of the ellipse are (-√3, 0), and (√3, 0)
iii) The coordinates of the covertex of an ellipse are;
(h, k + b), and (h, k - b)
Therefore, the coordinates of the covertex of the given ellipse are;
(0, 0 + 2·√2), and (0, 0 - 2·√2), which gives;
The covertex coordinates = (0, 2·√2), and (0, -2·√2)
iv) The length of the minor axis = 2×a
∴ The length of the minor axis = 2·√3
v) The length of the major axis = 2 × b
∴ The length of the major axis, = 2 × 2·√2 = 4·√2
vi) The length of the latus rectum, LR, is given as follows;
b > a, therefore;
\(LR = \dfrac{2 \cdot a^2}{b}\)
\(LR = \dfrac{2 \times 3}{2 \cdot \sqrt{2} } = \mathbf{ \dfrac{3 \cdot \sqrt{2} }{2}}\)
vii) Equation of directrices
a² = b²·(1 - e²)
3 = 8·(1 - e²)
e² = 1 - 3/8 = 5/8
The equation of the directrix, x = ± a/e
The equation of the directrix, x = ±(2·√2)/√(5/8) = ± 8·√5/5
viii) The focus of the ellipse, C² = 8 - 3 = 5
The equation of the latus rectum = b·e = √8 × √(5/8) = √5
Learn more about an ellipse here:
ttps://brainly.com/question/22404367
Adolto ran 6 laps on the track during practice His
average time per lap was 1.6 minutes. His times for
the first 5 laps were 1.5 minutes, 1.3 minutes, 1.5
minutes, 1.7 minutes, and 2.1 minutes. What was his
time for the last lap?
Answers
Answer:
1.5 minutes
Step-by-step explanation:
6 x 1.6 = 9.6
9.6 - 1.5 - 1.3 - 1.5 - 1.7 - 2.1 = 1.5
There are 3 denominations of bills in a wallet: $1, 5$, and $10. There are five fewer $5-bills than $1-bills. There are half as many $10-billsas $5-bills. If there are $115 altogether, find the number of each type of bill in the wallet.
Answers
Answer:
15 $1 bills
10 $5 bills
10 $10 bills
Step-by-step explanation:
Let x = number of $1 bills
"There are five fewer $5-bills than $1-bills."
The number of $5 bills is x - 5
"There are half as many $10-bills as $5-bills."
The number of $10 bills is (x - 5)/2.
A $1 bill is worth $1.
x $1 bills are worth x × 1 = x dollars
A $5 bill is worth $5.
x - 5 $5 are worth 5(x - 5) dollars.
A $10 bill is worth $10.
(x - 5)/2 $10 bills are worth 10(x - 5)/2 = 5(x - 5) dollars.
Now we add the value of each type of bills and set it equal to $115.
x + 5(x - 5) + 5(x - 5) = 115
x + 10(x - 5) = 115
x + 10x - 50 = 115
11x = 165
x = 15
There are 15 $1 bills.
$5 bills: x - 5 = 10 - 5 = 10
There are 10 $5 bills
$10 bills: (x - 5)/2 = (15 - 5)/2 = 5
There are 5 $10 bills
Answer: 15 $1 bills; 10 $5 bills; 10 $10 bills
Check:
First, we check the total value of the bills.
15 $1 bills are worth $15
10 $5 bills are worth $50
10 $10 bills are worth $50
$15 + $50 + $50 = $115
The total does add up to $115.
Now we check the numbers of bills of each denomination.
The number of $1 is 15.
The number of $5 is 5 fewer that 15, so it is 10.
The number of $10 bills is half the number of $5 bills, so it is 5.
All the given information checks out in the answer. The answer is correct.
A meteor crashed onto a planet and caused a crater that was 13,937.63 in deep.
Use the table of facts to find the depth of the crater in yards.
Round your answer to the nearest tenth.
Answers
The depth of the crater in yards is 387.2 yards
Converting Inches to yardsSince the crater is 13,937.63 in deep, we convert this to yards.
Since 36 in = 1 yard, we use this conversion factor to convert to yards
13,937.63 in × 1 yard/36 in = 387.16 yards
≅ 387.2 yards to the nearest tenth
So, the depth of the crater in yards is 387.2 yards
Learn more about conversion to yards here:
https://brainly.com/question/17342637
Please help will mark Brainly
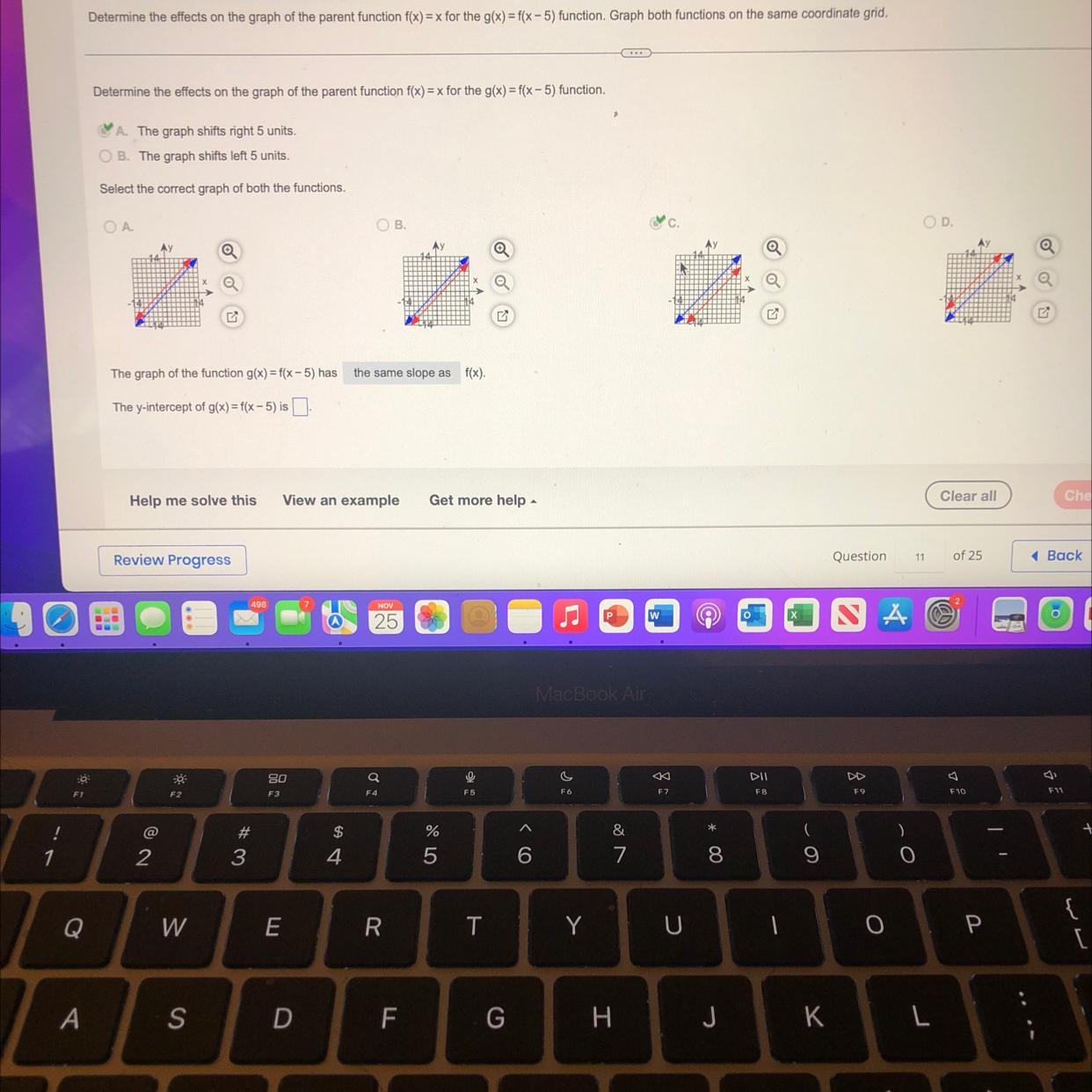
Answers
The function f(x) is shifted right to get g(x)
The graph is the graph (c)The slopes are equal and the y-intercept of g(x) is -5The effects of the transformationFrom the question, we have the following functions that can be used in our computation:
f(x) = x
g(x) = f(x - 5)
When a number is subtracted from x to get another function, it means that the initial function is shifted to the right by 5 units to get the new function
In this case, it means that f(x) is shifted right to get g(x)
The graph of the functionsRecall that
f(x) = x
g(x) = f(x - 5)
Also, note that:
The function f(x) is shifted right to get g(x)
if the function f(x) is the blue line, then the graph must be the graph (c)
This is so because the red line is to the right of the blue by 5 units
Also, it means that they have the same slope and the y-intercept of g(x) is -5
Read more about linear functions at
https://brainly.com/question/15602982
#SPJ1
Convert the equation f(t) = 227e b= -0.09€ to the form f(t) = ab* Give answers accurate to three decimal places
Answers
= 173.903t
Step-by-step Explanation:
The given equation is: f(t) = 227e^(b*t)
To convert it to the form f(t) = ab, we need to write it in the form of f(t) = a * e^(k*t), where a and k are constants.
Let's start by taking the natural logarithm (ln) of both sides:
ln(f(t)) = ln(227e^(b*t))
Using the properties of logarithms, we can simplify this to:
ln(f(t)) = ln(227) + ln(e^(b*t))
ln(f(t)) = ln(227) + b*t
Now, let's define a new constant, k = b, and rewrite the equation in terms of a and k:
ln(f(t)) = ln(a) + k*t
where a = 227 and k = -0.09
Taking the exponential of both sides, we get:
f(t) = e^(ln(a) + k*t)
f(t) = e^(ln(a)) * e^(k*t)
f(t) = a * e^(k*t)
Substituting the values of a and k, we get:
f(t) = 227 * e^(-0.09*t)
Therefore, the equation f(t) = ab is:
f(t) = 227e^(-0.09t) ≈ 173.903t (rounded to three decimal places)
helo please show work

Answers
Answer:
Step-by-step explanation:
Solution:
We can simplify the ratio 305 : 60 by dividing both terms by the greatest common factor (GCF).
The GCF of 305 and 60 is 5.
Divide both terms by 5.
305 ÷ 5 = 61
60 ÷ 5 = 12
Therefore:
305 : 60 = 61 : 12
A University of Florida economist conducted a study of Virginia elementary school lunch menus During the state-mandated testing period, school lunches average 863 calories The economist claims that after the testing period ends, the average caloric content of Virginia school lunches drops significantly They collected a random sample of 500 students' school lunches around Virginia
a). What null and alternative hypotheses should you test?
b). Set up the rejection region for this study using alpha = 0.05 Interpret alpha = 0.05 in the words of the problem
c). Suppose the sample data yielded the test statistic z = -2.17 What conclusion can you draw for the test?
d). Calculate the observed p-value for the test statistic z = -2.17 Interpret the p-value and draw the conclusion based on it
Answers
Answer:
a) Null hypothesis: \( \mu \geq 863\)
Alternative hypothesis: \( \mu >863\)
b) For this case using the significance level of \(\alpha=0.05\) we can use the normal standard distirbution in order to find a quantile who accumulates 0.05 of the area in the left and we got:
\( z_{\alpha}=-1.64\)
And the rejection zone would be:
\( z<-1.64\)
c) For this case since the statistic calculated is lower than the critical value we have enough evidence to reject the null hypothesis at 5% of significance
d) \( p_v = P(z<-2.17) =0.015\)
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at the significance level provided
Step-by-step explanation:
Part a
We want to test for this case if the true mean is significantly less than 863 calories so then the system of hypothesis are:
Null hypothesis: \( \mu \geq 863\)
Alternative hypothesis: \( \mu >863\)
Part b
For this case using the significance level of \(\alpha=0.05\) we can use the normal standard distirbution in order to find a quantile who accumulates 0.05 of the area in the left and we got:
\( z_{\alpha}=-1.64\)
And the rejection zone would be:
\( z<-1.64\)
Part c
For this case since the statistic calculated is lower than the critical value we have enough evidence to reject the null hypothesis at 5% of significance
Part d
For this case the p value would be given by:
\( p_v = P(z<-2.17) =0.015\)
Since the p value is lower than the significance level we have enough evidence to reject the null hypothesis at the significance level provided
In a small town 68% of the people owned television 72% on radio and 12% owned neither television nor radio (1)represent the information on a Veen diagram.
(2)what percentage of the population owned television.
Answers
Answer:
See attachment for Venn diagram
Percentage of only TV owners is 16%
Step-by-step explanation:
Given
\(TV\ Owners = 68\%\)
\(Radio\ Owners = 72\%\)
\(None = 12\%\)
Required
Represent with a Venn Diagram
What percentage owned television
From the Venn Diagram and In sets theory; we have that
Total = (TV Owners - Radio and TV Owners) + (Radio Owner - Radio and TV Owners) + Radio and TV Owners + None
Represent Radio and TV Owners with y
\(Total = (TV\ Owners - y) + (Radio\ Owner - y) + y + None\)
Substitute 68% for TV Owners, 72% for Radio Owners, 12& for None:
\(Total = 68\% - y + 72\%- y + y + 12\%\)
Collect Like Terms
\(Total = 68\% + 72\%+ 12\%- y + y - y\)
\(Total = 152\% - y\)
In Sets, Total represents 100%; So, we have
\(100\% = 152\% - y\)
Make y the subject of formula
\(y = 152\% - 100\%\)
\(y = 52\%\)
The percentage of only TV owners is calculated by subtracting y from TV owners
\(\%P = 68\% - 52\%\)
\(\%P = 16\%\)

Answer:
The answer is 90%
Step-by-step explanation:
Find sin A for the triangle below. Give the exact value as an expression and an approximation to the nearest ten-thousandth. Note: The triangle is not drawn to scale.
Answers
the exact value of sin A to the nearest ten- thousandth is 0. 6625
Using the pythagorean theorem
a² + b² = c²
The opposite side is unknown, so use the pythagorean theorem to find it
c = hypotenuse = 4
a= opposite site = ?
b= adjacent side = 3
Substitute into the formula
4² = a² + 3²
16 = a² + 9
a² = 16 -9 = 7
Find the square root
a =√7 = 2. 65
To find Sin A, use
Sin A = opposite side ÷ hypotenuse
Sin A = 2. 65 ÷ 4 = 0. 6625
Thus, the value of sin A is 0. 6625
Learn more about pythagorean theorem here:
https://brainly.com/question/654982
#SPJ1
) 65 people were asked on the activities they engage in during their free time. The results showed that 23 visit national parks, 26 engage in cycling while 22 engage in swimming. Furthermore 9 engage in swimming and visit national parks, 9 engage in swimming only while 11 visit national parks only. How many engage in
i. Swimming and cycling
Answers
Answer:
Step-by-step explanation:
i am working on the assumption that nobody does all three of them
i got 4 because including the people that do swimming and park, the total number of people that do swimming is 22.
the same logic goes for cycling: including the people that do swimming and visit the national park, the total is 23.
so that means that find how many people do swimming and cycling, we have to add the people doing only swimming, with the people doing both swimming and park and then subtract that answer from 22 which gives you 4

if the relation represents a function, find the domain and range. (enter your answers using interval notation. if the relation is not a function, enter none in the domain and range answer blanks.)
Answers
If the relation is represented by the equation y = 2x + 1, the domain would be all real numbers (-infinity, +infinity) and the range would be all real numbers greater than or equal to 1 (1, +infinity).
A relation is a function if for every input (x) there is exactly one output (y). To determine if a relation is a function, we can use the vertical line test, which states that if a vertical line can be drawn through the graph and intersects the relation more than once, then the relation is not a function.
If the relation is a function, we can find the domain and range by analyzing the relation. The domain is the set of all x-values and the range is the set of all y-values. In interval notation, the domain is written as (a, b) and the range is written as (c, d).
So, the domain and range answers depend on the relation which is given and it should be specified.
Read more about Functions:
https://brainly.com/question/22340031
#SPJ4
What are the solutions of the equation x4 – 9x2 + 8 = 0? Use u substitution to solve. x = 1 and x = 2 StartRoot 2 EndRoot x = ±1 and x = plus-or-minus 2 StartRoot 2 EndRoot x = ±i and x = plus-or-minus 2 i StartRoot 2 EndRoot x = ±i and x = 2 StartRoot 2 EndRoot
Answers
Answer:
The solutions are
x = -1, 1, -2√2, and 2√2.
Step-by-step explanation:
Given the equation
x^4 - 9x² + 8 = 0
Let u = x², then the equation becomes
u² - 9u + 8 = 0
u² - u - 8u + 8 = 0
(u² - u) - (8u - 8u) = 0
u(u - 1) - 8(u - 1) = 0
(u - 8)(u - 1) = 0
u - 8 = 0
=> u = 8
Or
u - 1 = 0
=> u = 1
For u = 8
=> x² = 8
=> x = ±√8 = ±2√2
For u = 1
=> x² = 1
=> x = ±√1 = ± 1
Answer:
B
Step-by-step explanation:
12. In 2010. Utah had a population of about2.8 X 106. The same year, Wyoming had apopulation of about 5.6 x 105.Which statement correctly compares thepopulation of these states?
Answers
Divide the population of Utah by the poputlation of Wyoming
\(\begin{gathered} \frac{Population\text{ of Utah}}{Population\text{ of Wyoming}}=\frac{2.8\times10^6}{5.6\times10^5} \\ \frac{Population\text{ of Utah}}{Population\text{ of Wyoming}}=\frac{2.8\times10\times10^5}{5.6\times10^5} \\ \frac{Population\text{ of Utah}}{Population\text{ of Wyoming}}=\frac{28\times10^{}}{56^{}} \\ \frac{Population\text{ of Utah}}{Population\text{ of Wyoming}}=\frac{280}{56} \\ \frac{Population\text{ of Utah}}{Population\text{ of Wyoming}}=\frac{5}{1} \\ Population\text{ of Utah=5(}Population\text{ of Wyoming)} \end{gathered}\)Thus, Population of Utah is 5 times the population
Is 1/4 a rational number, integer, whole number, natural, or irrational number? And is -5/2 either aswell?
Answers
Answer:SOMEONE PLZZZ ANSWER THIS I NEED THE ANSWER TO!!!!!!!!!!!!!!!!!!!!!!!!!!!
Step-by-step explanation:
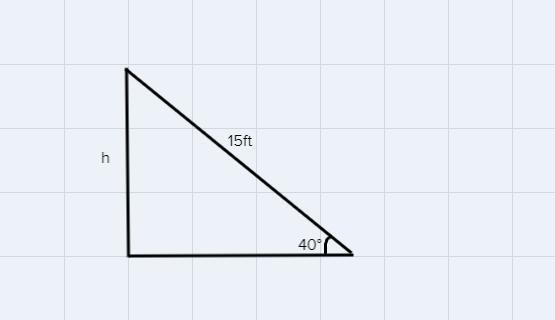
this sliding board as shown is 15 feet long and meets the ground at a 40 degree angle. what is the height of the ladder to the nearest tenth?sin 40 degrees= 0.6428cos 40 degrees= 0.7660
Answers
Imagine the situation described as a triangle.
They are asking to find the height h, to do this, you can use the sine and the length of the sliding board.
\(\begin{gathered} \sin 40=\frac{h}{15} \\ \sin 40\cdot15=h \\ 0.6428\cdot15=h \\ h=9.642\approx9.6 \end{gathered}\)The height of the ladder is 9.6 feet.
Can you find the surface area and volume pls? ITS WORTH 50 points

Answers
Answer:
Solution given:
r=4in
h=4in
surface area=2πr(r+h)=2π*4(4+4)=64π or201.06ft²
Volume=πr²h=π*4²*4=64π or 201.06ft³
Which of the following results in the difference of two squares?

Answers
The difference of two squares expression is (c) (5x + 3y)(5x - 3y)
How to determine the difference of two squares?The difference of two squares expression is represented as:
a^2 - b^2 = (a + b)(a - b)
Using the above as a guide, we have the following expression in option (c)
(5x + 3y)(5x - 3y)
Hence, the difference of two squares expression is (c) (5x + 3y)(5x - 3y)
Read more about difference of two squares at:
https://brainly.com/question/914765?referrer=searchResults
#SPJ1
2 increased by 6 times 4
Answers
Answer:
(2+6)+4 = (8)+4 = 12
Step-by-step explanation:
Add the constant of 6 to the constant of 2
2+6
Add the constant 4 to the terms of (2+6)
(2+6)+4
there you go! there's your algebraic expression!