HELP PLZ WILL MARK U BRAINLIEST
9x2 - 4x + 2
2x2 + 9x - 3
Answers
1. -4x+20
2. 9x+1
Explanation:
I’m different
Related Questions
A line is perpendicular to y = -1/5x + 1 and intersects the point negative (-5,1) what is the equation of this perpendicular line?
Answers
Answer: y = 5x + 26
Step-by-step explanation:
To find the equation of a line that is perpendicular to the given line y = -1/5x + 1 and passes through the point (-5, 1), we need to determine the slope of the perpendicular line. The given line has a slope of -1/5. Perpendicular lines have slopes that are negative reciprocals of each other. So, the slope of the perpendicular line will be the negative reciprocal of -1/5, which is 5/1 or simply 5. Now, we have the slope (m = 5) and a point (-5, 1) that the perpendicular line passes through.
We can use the point-slope form of a linear equation to find the equation of the line:
y - y1 = m(x - x1)
Substituting the values, we get:
y - 1 = 5(x - (-5))
Simplifying further:
y - 1 = 5(x + 5)
Expanding the brackets:
y - 1 = 5x + 25
Rearranging the equation to the slope-intercept form (y = mx + b):
y = 5x + 26
Therefore, the equation of the perpendicular line that passes through the point (-5, 1) is y = 5x + 26.
Does the point (4, -4) satisfy the equation y = -x?
yes
no
Answers
Answer:
noo
because we know that (x,y) is the situation
nd the solution in yr question here y is( -)
hope it helps
Answer:
no
Step-by-step explanation:
( x, y ) = ( 4, - 4 )
Here,
x = 4
y = - 4
y ≠ - x
The inverse of a number is it’s _______?
Answers
Answer:
negation
Step-by-step explanation:
Other options include: opposite, sign change
The weight of a television is 1/4 of that of a refrigerator. If the television is 51 kg lighter than the refrigerator, find the weight of the television.
Answers
54:56
Which table shows a constant of proportionality of 2 for the ratio of string instruments to percussion instruments?
String
2
4
B
Percussion
3
6
9
String
2.
4
6
Percussion
5
10
15
String
2
4
6
Percussion
1
2
3
String
2
4
B
Percussion
4
8
12
Mark this and return
Save and Exit
Next
Sub
Answers
Answer:
String
2.
4
6
Percussion
5
10
15
Step-by-step explanation:
PLEASE HELP I WILL GIVE BRAINLIEST TO RIGHT ANSWERS ONLY
2^(x)= 7 Write the following exponential equation into its equivalent logarithmic form
Answers
Answer:
logb(x y) = y ∙ logb(x)
Step-by-step explanation:
1/5 de los animales en el zoológico son monos 5/7 de los monos son machos
¿Qué fracción de los animales en el zoológico son monos machos?
Answers
1/7 of the animals in the zoo are male monkeys.
What fraction of the animals in the zoo are male monkeys? Explain with workings.
To find the fraction of animals in the zoo that are male monkeys, we have to calculate the product of the fractions representing the proportion of monkeys and the proportion of male monkeys among them.
Given that 1/5 of the animals in the zoo are monkeys, we will then represent this as:
= 1/5
= 5/25.
And 5/7 of the monkeys are male which is written as 5/7.
To get fraction of male monkeys, we will multiply these two fractions:
= (5/25) * (5/7)
= 25/175
= 1/7.
Full question:
1/5 of the animals in the zoo are monkeys 5/7 of the monkeys are male. What fraction of the animals in the zoo are male monkeys?
Read more about fraction
brainly.com/question/17220365
#SPJ1
Solve the following system of equations (given in (5) of Section 7.6) when E = 60 V, L = 2 h, R = 50 2, C = 10-4 f, 17(0) = 0, and 12(0) = 0. dii L + Ri2 = E(t) dt diz RC + 12 - 11 = 0 dt 11(t) iz(t)
Answers
The solution to the given system of equations, with the given values of E, L, R, C, 17(0), and 12(0), is i(t) = (E/R) + A exp(-(R/L)t)sin(ωt), and v(t) = Ecos(ωt) - (Li(t))/R - (Q(0)/C)exp(-(1/RC)t), where A = -((E/R) + 11(0)) and ω = sqrt(1/(LC) - (R/(2L))^2).
Using Kirchhoff's laws, we can derive the following system of equations:
dii L + Ri2 = E(t) ...(1)
diz RC + 12 - 11 = 0 ...(2)
dt 11(t) iz(t)
Substituting the given values of E, L, R, and C, we get:
dii 2 + 100i2 = 60 ...(3)
diz 10-4 + 12 - 11 = 0 ...(4)
dt 11(t) iz(t)
We can solve equation (3) by first finding the general solution to the homogeneous equation (i.e., the equation without the right-hand side):
dii 2 + 100i2 = 0
The characteristic equation is λ^2 + 100 = 0, which has roots ±10i. Therefore, the general solution to the homogeneous equation is:
i(t) = A exp(-(R/L)t)sin(ωt)
where A is a constant and ω = sqrt(1/(LC) - (R/(2L))^2).
To find the particular solution to equation (3), we can use the method of undetermined coefficients. We assume that the particular solution has the form i(t) = (E/R) + B, where B is a constant. Substituting this into equation (3), we get:
dB/dt = 0
Integrating both sides, we get B = (E/R) + 11(0).
Therefore, the general solution to equation (1) is:
i(t) = (E/R) + A exp(-(R/L)t)sin(ωt) - (E/R) - 11(0)
i(t) = A exp(-(R/L)t)sin(ωt) - 11(0)
To solve equation (2), we first rearrange it as:
diz/dt = -(1/RC)iz(t) - 12/RC
This is a first-order linear homogeneous differential equation, which has the general solution:
iz(t) = Q(0)exp(-(1/RC)t)
where Q(0) is the initial charge on the capacitor.
Finally, we can find the voltage across the capacitor using Ohm's law:
v(t) = E - Li(t) - iz(t)/C
Substituting the values of i(t) and iz(t), we get:
v(t) = Ecos(ωt) - (Li(t))/R - (Q(0)/C)exp(-(1/RC)t)
Therefore, the solution to the given system of equations, with the given values of E, L, R, C, 17(0), and 12(0), is i(t) = (E/R) + A exp(-(R/L)t)sin(ωt), and v(t) = Ecos(ωt) - (Li(t))/R - (Q(0)/C)exp(-(1/RC)t), where A = -((E/R) +
For more questions like Equation click the link below:
https://brainly.com/question/16663279
#SPJ11
divide 70 into the ratio of 2:5
Answers
Answer:
20 : 50
Step-by-step explanation:
sum the parts of the ratio , 2 + 5 = 7 parts
divide 70 by 7 to find the value of one part of the ratio
70 ÷ 7 = 10 ← value of 1 part of the ratio , then
2 parts = 2 × 10 = 20
5 parts = 5 × 10 = 50
then
50 divided in the ratio 2 : 5 is 20 : 50
simplify the following expression: 2^-3÷2^5
Answers
Answer:
Exact Form:
1/256
Decimal Form:
0.00390625
Step-by-step explanation:
GIVING BRAINLIEST!! The 47 members of the glee club are trying to raise at least $6,000 so they can compete in the state championship. They already have $1,260. What inequality can you enter to find the amount each member must raise, on average, to meet the goal?

Answers
Answer:
couch
Step-by-step explanation:
What is this problem

Answers
The coordinate of the vertex is; (h, k) = (3, -5)
The final equation of the parabola is; y = 5(x - 3)² - 5
How to find the vertex of a Parabola?The vertex is the coordinate of the crest or trough of the curve. Now, in the given graph, we only have a Trough which is the lowest point of the graph.
The coordinate of the vertex is; (h, k) = (3, -5)
2) Since the general equation is;
y = a(x - h)² + k
We will have;
y = a(x - 3)² - 5
At x = 2, y = 0. Thus;
0 = a(2 - 3)² - 5
a - 5 = 0
a = 5
3) The final equation of the parabola is;
y = 5(x - 3)² - 5
Read more about Parabola Vertex at; https://brainly.com/question/17987697
#SPJ1
Determine if the two triangles are congruent. If they are, state how you know.
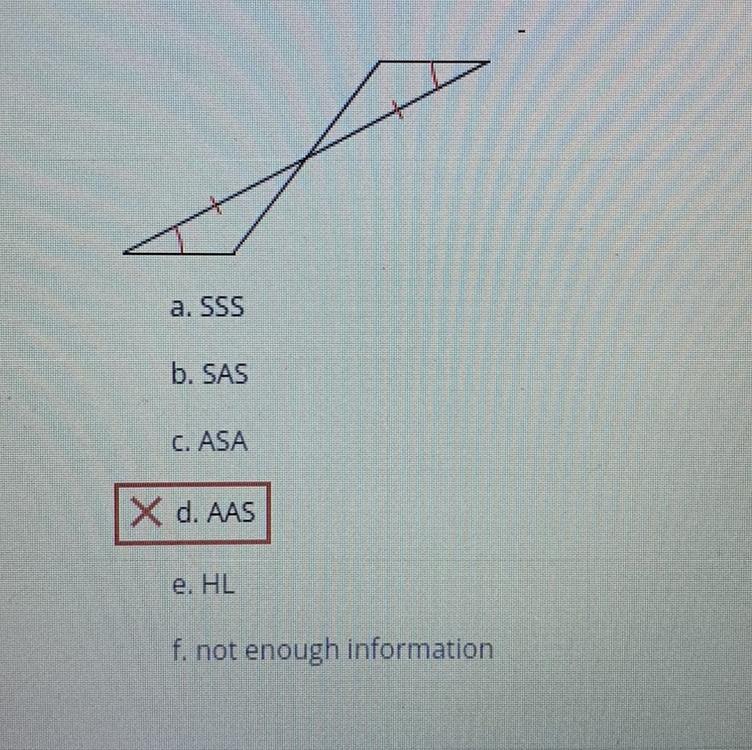
Answers
Answer:
because they mirror eachother, they both have two acute angles and an obtuse angle. they are both obtuse triangles
Answer:
b, sas
Step-by-step explanation:
i don't understand this one very well, but i believe it to be b, side-angle-side.
Monica found the volume of the prism below using the expression .
What errors did Monica make? Check all that apply.
She should have counted only 2 unit cubes instead of 4.
She should have counted 8 one-third cubes instead of only 4.
She should have found the total value of the one-third cubes by multiplying by instead of by .
Each fractional cube is worth instead of the that she used.
She cannot stack more than one layer of fractional cubes in a prism.
Answers
Answer:
See Explanation
Step-by-step explanation:
The expression and the dimension of the prism are not given.
So, I will just give a general expression.
The volume of a prism is:
\(Volume = Length * Width * Height\)
Assume that:
\(Length = 2\)
\(Width = 2\)
\(Height = 1\frac{2}{3}\)
See attachment
Monica's expression should be:
\(Volume = 2 * 2 * 1\frac{2}{3}\)
And the solution will be:
\(Volume = 2 * 2 * \frac{5}{3}\)
\(Volume = \frac{20}{3}\)

Answer:
b and c
Step-by-step explanation:
i took the test <3
Give the linear inequality shown in the graph below.
Group of answer choices
x≥−3
y>−3
y≥−3
x>−3

Answers
The measures of the angles of a triangle are shown in the figure below. Solve for x.

Answers
Answer:
63°
Step-by-step explanation:
Triangle= 180°
=180°-90°-27°
=90°-27°
=63°
Answer:
63°
Step-by-step explanation:
90° + 27°= 117°
180°- 117°= 63°
What is the constant term of -3x² - 7x + 2?
Answers
Answer:
2
a=-3 , b=-7 , c=2
a=quadratic term
b=linear term
c=constant term
Find fx, fy, fx(4,1), and fy(-1, -3) for the following equation. f(x,y)=√√x² + y² fx= (Type an exact answer, using radicals as needed.) fy=0 (Type an exact answer, using radicals as needed.) fx(
Answers
The partial derivatives of \(fx\)= x / (√(x² + y²)) , \(fy\) = y / (√(x² + y²)),
\(fx(4, 1)\)= 4 / (√17) and \(fy(-1, -3)\) = -3 / (√10).
Let's calculate the partial derivatives of \(f(x, y)\) = √(√(x² + y²)).
To find \(fx\), we differentiate \(f(x, y)\) with respect to x while treating y as a constant. Using the chain rule, we have:
\(fx\) = (∂f/∂x) = (∂/∂x) √(√(x² + y²)).
Using the chain rule, we obtain:
\(fx\) = (∂/∂x) (√(x² + y²))^(1/2).
Applying the power rule, we have:
\(fx\) = (1/2) (√(x² + y²))^(-1/2) (2x).
Simplifying further, we get:
\(fx\) = x / (√(x² + y²)).
Next, let's calculate \(fy\) by differentiating \(f(x, y)\) with respect to y while treating x as a constant.
Using the chain rule, we have:
\(fy\) = (∂f/∂y) = (∂/∂y) √(√(x² + y²)).
Using the chain rule and the power rule, we obtain:
\(fy\) = (1/2) (√(x² + y²))^(-1/2) (2y).
Simplifying, we get:
\(fy\) = y / (√(x² + y²)).
To evaluate \(fx(4, 1)\), we substitute x = 4 into the expression for \(fx\):
\(fx(4, 1)\) = 4 / (√(4² + 1²)) = 4 / (√17).
To evaluate \(fx(4, 1)\) we substitute y = -3 into the expression for \(fy\):
\(fy(-1, -3)\)= -3 / (√((-1)² + (-3)²)) = -3 / (√10).
Therefore, the exact values are \(fx(4, 1)\)= 4 / (√17) and \(fy(-1, -3)\)= -3 / (√10).
learn more about derivative here:
https://brainly.com/question/29020856
#SPJ11
Please help whoever answers this correctly I'll mark your answer brainliest

Answers
Answer: The 2nd and 3rd one are correct
Step-by-step explanation:
After reflecting it, the square itself would not change, only the position of the square. Therefore, the same line segments from the beginning which were given would be parallel.
False, True, True.
PQ and PS cannot be parallel, because there is two P's in the first one.
which angle is this??

Answers
Answer:
acute
Step-by-step explanation:
the angles are all less than 90°
they are not equal so not equialteral
has to be acute
which method represents a correct way to solve the equation 2(t−5)=48?
Answers
The solution to the equation 2(t - 5) = 48 is t = 29.
To solve the equation 2(t - 5) = 48, we can use the following steps:
Distribute the 2 to the terms inside the parentheses:
2t - 10 = 48
Add 10 to both sides of the equation to isolate the variable term:
2t = 58
Divide both sides of the equation by 2 to solve for t:
t = 29
Know more about equation here:
https://brainly.com/question/29657983
#SPJ11
please help!!! I dont know which ones....

Answers
Answer:
g(x) =1
x-1
it's either g(x) or f(x)
Write a quadratic function f whose zeros are -3 and -8
Answers
Answer:
y = x² + 11x + 24
Step-by-step explanation:
y = (x + 3)(x + 8)
Expand
y = x² + 8x + 3x + 24
Combine like terms
y = x² + 11x + 24
there are two misshapen coins in a box; the probabilities they land heads when flipped are 0.4 and 0.7. one of the coins is to be randomly chosen and flipped 10 times. given that exactly two of the first three flips landed heads, what is the conditional expected number of heads in the 10 flips?
Answers
The conditional expected number of heads in the 10 flips, given that exactly two of the first three flips landed heads, can be calculated by taking the weighted average of the expected number of heads for each coin. Using the probabilities of choosing each coin and the conditional probabilities of obtaining two heads in three flips for each coin, the conditional expected number of heads can be determined.
To solve this problem, we need to use conditional probability and expected value concepts. Let's denote the event of choosing the 0.4 probability coin as A and the event of choosing the 0.7 probability coin as B. We need to calculate the conditional expected number of heads in the 10 flips given that exactly two of the first three flips landed heads.
First, we calculate the probability of choosing each coin. Since there are two coins in the box and they are equally likely to be chosen, the probability of choosing each coin is 0.5.
Next, we calculate the conditional probability of obtaining exactly two heads in the first three flips given that coin A is chosen. The probability of getting exactly two heads in three flips with a 0.4 probability coin is given by the binomial distribution formula: P(2 heads in 3 flips | A) = (3 choose 2) * (0.4)² * (1 - 0.4).
Similarly, we calculate the conditional probability of obtaining exactly two heads in the first three flips given that coin B is chosen. The probability of getting exactly two heads in three flips with a 0.7 probability coin is:
P(2 heads in 3 flips | B) = (3 choose 2) * (0.7)² * (1 - 0.7).
Using these probabilities, we can calculate the conditional expected number of heads in the 10 flips by taking the weighted average of the expected number of heads for each coin. The conditional expected number of heads in the 10 flips is given by: (0.5 * P(2 heads in 3 flips | A) * 10) + (0.5 * P(2 heads in 3 flips | B) * 10).
By substituting the calculated values into this formula, we can find the conditional expected number of heads in the 10 flips given that exactly two of the first three flips landed heads.
Learn more about probability here: https://brainly.com/question/31828911
#SPJ11
find the differential of the function. z = e−9x cos(6t) dz = dx dt
Answers
Therefore, The differential of the function z = e−9x cos(6t) with respect to both x and t is given by dz = (∂z/∂x)dx + (∂z/∂t)dt.
The differential of the function z = e−9x cos(6t) with respect to both x and t is given by dz = (∂z/∂x)dx + (∂z/∂t)dt.
Using the chain rule, we find that ∂z/∂x = -9e^(-9x)cos(6t) and ∂z/∂t = -6e^(-9x)sin(6t).
Substituting these values, we get dz = (-9e^(-9x)cos(6t)dx) + (-6e^(-9x)sin(6t)dt).
The differential of a function is a measure of the sensitivity of the function to small changes in its inputs. In this case, we are asked to find the differential of the function z = e^-9x cos(6t) with respect to both x and t. To do this, we use the chain rule to find the partial derivatives of z with respect to x and t, and then substitute them into the formula for the total differential. The resulting differential dz represents the change in z due to small changes in both x and t.
Therefore, The differential of the function z = e−9x cos(6t) with respect to both x and t is given by dz = (∂z/∂x)dx + (∂z/∂t)dt.
To learn more about the linear function visit:
brainly.com/question/29612131
#SPJ11
On saturdays, cars arrive at sami schmitt's scrub and shine car wash at the rate of 6 cars per fifteen minute interval. Using the poisson distribution, the probability that five cars will arrive during the next five minute interval is.
Answers
The probability that five cars will arrive during the next thirty minute interval is 0.0361
What is probability?
Probability is a way of calculating how likely something is to happen. Numerous things are difficult to forecast with absolute confidence.
Main Body:
Let X = number of cars arriving at Sami Schmitt's Scrub and Shine Car Wash.
The average number of cars arriving in 15 minutes is 6.
The average number of cars arriving in 1 minute is = 6/15 = 2/5
The average number of cars arriving in 5 minutes is, (2/5)*5 = 2
The random variable X follows a Poisson distribution with parameter λ = 2.
The probability mass function of X is:
P(X=\(x\)) = \((e^{-2} 2^{x} )/x!\) , x = 0,1 ,2 ,3...
Compute the probability that 5 cars will arrive in 5 minutes as follows:
P(X=5) =\((e^{-2} 2^{5} )/5!\)
P (X= 5) = 0.0361
Hence probability is 0.0361
to learn more about probability , visit;
https://brainly.com/question/24756209
#SPJ4
A plane traveled 336 miles to Carson City and back. The trip there was with the wind. It took 4 hours. The trip back was into the wind. The trip back took 6 hours. What is the speed of the plane in still air? What is the speed of the wind?
Answers
Answer:
Thus, train speed = 70 mph while wind speed is. y = 14 mph
Step-by-step explanation:
Let x = speed of the plane in mph.
Let y = speed of wind in mph.
We are told that The trip there was with the wind. It took 4 hours. The trip back was into the wind. The trip back took 6 hours.
Formula for distance is;
Distance = speed × time
Thus;
(x + y)4 = 336
(x + y) = 84 - - - - (1)
Also;
(x - y)6 = 336
Divide both sides by 6
(x - y) = 56 - - - (eq 2)
Add eq 1 and 2 to give;
2x = 84 + 56
2x = 140
x = 140/2
x = 70 mph
Plug in 70 mAh for x in eq 1.
(70 - y) = 56
y = 70 - 56
y = 14 mph
Thus, train speed = 70 mAh while wind speed is. y = 14 mph
The value of a car in 1990 is 7700 dollars and the value is expected to go down by 390 dollars per year for the next 10 years.
Answers
The value of the car in 2000 is expected to be $3800, given a starting value of $7700 in 1990 and a decrease of $390 per year for 10 years.
To find the value of the car in each subsequent year, we can subtract $390 from the previous year's value. Let's calculate the value of the car for each year from 1990 to 2000.
Year 1990: $7700
Year 1991: $7700 - $390 = $7310
Year 1992: $7310 - $390 = $6920
Year 1993: $6920 - $390 = $6530
Year 1994: $6530 - $390 = $6140
Year 1995: $6140 - $390 = $5750
Year 1996: $5750 - $390 = $5360
Year 1997: $5360 - $390 = $4970
Year 1998: $4970 - $390 = $4580
Year 1999: $4580 - $390 = $4190
Year 2000: $4190 - $390 = $3800
Therefore, the value of the car is expected to be $3800 in the year 2000.
To know more about value visit -
brainly.com/question/13650541
#SPJ11
How to measure circumference without pi.
Answers
Answer:
use the line segment instead
Find the derivative of the function. y = arctan √[(1 − x) /(1 + x)]
y' = ?
and
Find the derivative of the function. y = 3tan−1 [x − √(1 + x^2)]
y' = ?
Answers
The derivative function for equations 1 and 2 will be
y' = -1/ [2√(1-x²)] and y' = 3/[2(1 + x²)] respectively
Here we need to find the derivative of
\(y = tan^{-1}\sqrt{\frac{1-x}{1+x} }\)
Let x = cos2z
Hence we get
\(y = tan^{-1}\sqrt{\frac{1-cos2z}{1+cos2z} }\)
\(or, y = tan^{-1}\sqrt{\frac{2sin^{2}z}{2cos^{2}z} }\)
\(or, y = tan^{-1}(tanz)\)
or, y = z
Hence dy/dx = dz/dx
We know that
x = cos2z
or, 2z = cos⁻¹x
or, 2 dz/dx = -1/√(1-x²)
Hence dy/dx = -1/ [2√(1-x²)]
The second equation is
\(y = 3tan^{-1}[x-\sqrt{1+x^{2}} ]\)
Let x = cotz
Hence we get
\(y = 3tan^{-1}[cotz-\sqrt{1+cot^{2}z} ]\)
\(y = 3tan^{-1}[cotz-\sqrt{cosec^{2}z} ]\)
or, y = 3tan⁻¹ [cotz - cosecz]
or, y = 3tan⁻¹ [cosz/sinx - 1/sinz]
or, y = 3tan⁻¹ [(cosz - 1)/sinz]
or, y = 3tan⁻¹ [-2sin²(z/2)/{2sin(z/2) cos(z/2)}]
or, y = 3tan⁻¹ [-sin(z/2)/cos(z/2)]
or, y = 3tan⁻¹ [-tan{z/2)]
or, y = 3tan⁻¹ [tan{-z/2)]
or, y = -3z/2
or, dy/dz = -3/2 dz/dx
We have
x = cotz
or, z = cot⁻¹z
or, dz/dx = -1/(1 + x²)
Hence we get
dy/dx = 3/[2(1 + x²)]
To learn more about differentiation visit
https://brainly.com/question/27986235
#SPJ4