Answers
Answer:
75% of 124 is 93.
Step-by-step explanation:
I hoped this helped ^^
Related Questions
Please help me solve this...
Use the given information about a polynomial function to write the equation.
Degree 4. Root of multiplicity 2 at x=-2, and roots with multiplicity of 1 at x=6
and x=2. y-intercept at (0,10)
Answers
Answer:
\(\displaystyle f(x)=\frac{5}{24}(x+2)^2(x-6)(x-2)\)
Step-by-step explanation:
The standard, factored polynomial function is given by:
\(f(x)=a(x-p)^n(x-q)^m...\)
Where a is the leading coefficient,
p and q are factors,
And n and m are the powers or multiplicity they are being raised to.
We know that our polynomial function is of degree 4.
We have a root of multiplicity of 2 at x=-2.
So, our factor is:
\((x-(-2))=(x+2)\\\)
It is has a multiplicity of 2, it is squared. So:
\((x+2)^2\)
We have another root with multiplicity of 1 at x=6.
So, our factor is:
\((x-6)\)
And since it is to the first power, we can write it as is.
Finally, we have another root of multiplicity of 1 at x=2.
So, our factor is:
\((x-2)\)
Therefore, our entire function is:
\(f(x)=a(x+2)^2(x-6)(x-2)\)
We still have to determine our leading coefficient, a.
We can use that y-intercept. The y-intercept is at (0, 10). So, when x=0, y=10. By substitution:
\(10=a(0+2)^2(0-6)(0-2)\)
Evaluate:
\(10=a(4)(-6)(-2)\)
Multiply:
\(10=48a\)
Therefore:
\(\displaystyle a=\frac{10}{48}=\frac{5}{24}\)
Therefore, our final function is:
\(\displaystyle f(x)=\frac{5}{24}(x+2)^2(x-6)(x-2)\)
For the question of total area of the cuboid is 200cm^.
I understand where we divide 150 by 4.
But why do I need to multiply by 5, when there are 6 faces.
Answers
You need to multiply by 5 instead of 6 because each pair of opposite faces on a cuboid has the same area, so by considering one face from each pair, you ensure that you don't count any face twice.
When calculating the total surface area of a cuboid, you need to understand the concept of face pairs.
A cuboid has six faces, but each face has a pair that is identical in size and shape.
Let's break down the reasoning behind multiplying by 5 instead of 6 in the given scenario.
To find the surface area of a cuboid, you can add up the areas of all its faces.
However, each pair of opposite faces has the same area, so you avoid double-counting by only considering one face from each pair. In this case, you have five pairs of faces:
(1) top and bottom, (2) front and back, (3) left and right, (4) left and back, and (5) right and front.
By multiplying the average area of a pair of faces by 5, you account for all the distinct face pairs.
Essentially, you are considering one face from each pair and then summing their areas.
Since all the pairs have the same area, multiplying the average area by 5 gives you the total surface area.
When dividing 150 by 4 (to find the average area of a pair of faces), you are essentially finding the area of a single face.
Then, by multiplying this average area by 5, you ensure that you account for all five pairs of faces, providing the total surface area of the cuboid.
Thus, multiplying by 5 is necessary to correctly calculate the total surface area of the cuboid by accounting for the face pairs while avoiding double-counting.
For similar question on cuboid.
https://brainly.com/question/29568631
#SPJ8
What is the total surface area

Answers
Answer:
Step-by-step explanation:

Solve:
|x-7|<-1.
zero solutions
one solution
infinite solutions
all real numbers
Answers
Step-by-step explanation:
In mathematics, the absolute value |x|, is the non-negative result of x without regard to its sign.
An absolute function, can never have a negative result.
By this alone, you can solve the question because the inequality is false, and therefore there are zero solutions.
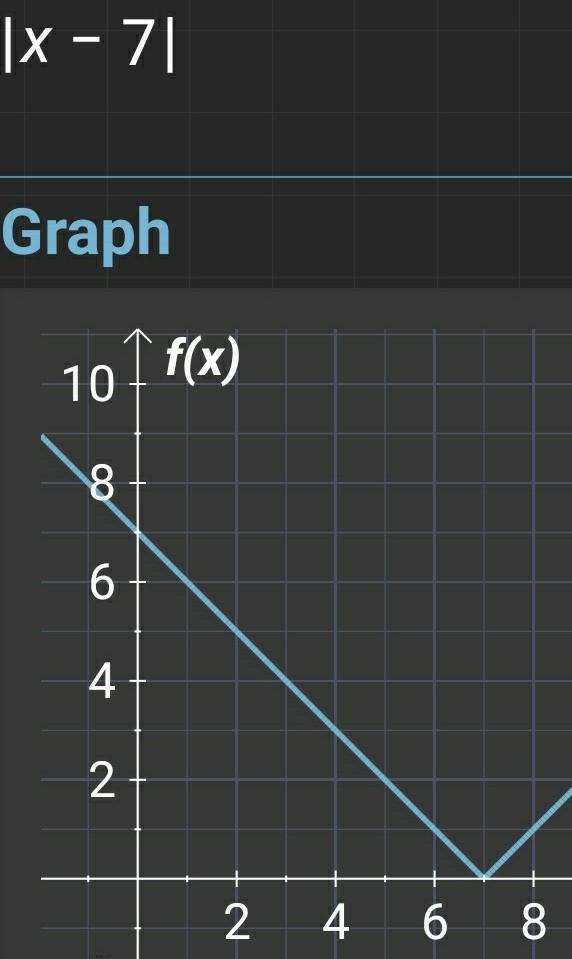
Please see the attachment of f(x) = |x - 7|.
When you look at the graph, you can easily confirm that there is no value which can result in a negative y- coordinate like -2. In fact, that is the whole purpose of any absolute value or function. The result of an absolute function can never be negative.
g a box has a square base of side x and height h find the dimensions x, h for which the volume is 14 and the surface area is as small as possible
Answers
Answer:
Step-by-step explanation:
Base area =\(x^2\)
side area=\(h*x\)
Volume=\(x^2*h\)=14
Surface area =\(4hx+2x^2\)
upon substituting \(h=14/x^2\)
surface area = \(4*\frac{14}{x^2}*x+2x^2\)
upon differentiating and solving we get f"(\(\sqrt[3]{14\\}\)) >0 proves that this point is of minima
hence, dimensions are
\(x=\sqrt[3]{14}\) ,h=\(\sqrt[3]{14}\)
Random simple service of voters were taken in three different regions of a county that has a voter population of 55,000. On average 42 out of 100 voters supported issue seven and 58 oppose it estimated number of voters in the county who support the issue.

Answers
Answer: 23100 voters
Step-by-step explanation:
42*55000=2310000
2310000/100=23100 voters
Attached as an image. Please help.

Answers
The general solution of the logistic equation is y = 14 / [1 - C · tⁿ], where a = - 14² / 3 and C is an integration constant. The particular solution for y(0) = 10 is y = 14 / [1 - (4 / 10) · tⁿ], where n = - 14² / 3.
How to find the solution of an ordinary differential equation with separable variablesHerein we have a kind of ordinary differential equation with separable variables, that is, that variables t and y can be separated at each side of the expression prior solving the expression:
dy / dt = 3 · y · (1 - y / 14)
dy / [3 · y · (1 - y / 14)] = dt
dy / [- (3 / 14) · y · (y - 14)] = dt
By partial fractions we find the following expression:
- (1 / 14) ∫ dy / y + (1 / 14) ∫ dy / (y - 14) = - (14 / 3) ∫ dt
- (1 / 14) · ln |y| + (1 / 14) · ln |y - 14| = - (14 / 3) · ln |t| + C, where C is the integration constant.
y = 14 / [1 - C · tⁿ], where n = - 14² / 3.
If y(0) = 10, then the particular solution is:
y = 14 / [1 - (4 / 10) · tⁿ], where n = - 14² / 3.
To learn more on differential equations: https://brainly.com/question/14620493
#SPJ1
Find the sum of the first 9 terms of the following sequence. Round to the nearesthundredth if necessary.40,-16,32/5
Answers
SOLUTION
The following sequence is a geometric series and we have been provided with the formula
\(S_n=\frac{a_1-a^{}_1r^n}{1-r}\)Here a1 is the first term = 40,
r is the common ratio = -0.4 (to get r, divide the second term by the first term)
n = number of terms = 9. Now let's solve
\(\begin{gathered} S_n=\frac{a_1-a^{}_1r^n}{1-r} \\ \\ S_9=\frac{40_{}-40\times(-0.4)^9}{1-(-0.4)} \\ \\ S_9=\frac{40_{}-(-0.0105)^{}}{1+0.4} \\ \\ S_9=\frac{40_{}+0.0105^{}}{1+0.4} \\ \\ S_9=\frac{40.0105^{}}{1.4} \\ \\ S_9=28.5789 \end{gathered}\)The sum to the nearest hundredth becomes = 28.58
if the sum of the interior angles of a polygon is 4 right angles, then the polygon is a?
Answers
Answer:
square or rectangle
Step-by-step explanation:
Consider the function A defined by the rule A(x) = integral^x_1 f(t) dt, where f(t) = 4 - 2t. use the first fundamental theorem of calculus to find an equivelant formula that does not involve integrals
Answers
The equivalent formula that does not involve integrals is A(x) = 2x - 2x^2 + 4x - 4.
The First Fundamental Theorem of Calculus states that if f(x) is a continuous function on the interval [a, b], then the function F(x) = integral^x_a f(t) dt is an antiderivative of f(x), meaning that its derivative is equal to f(x). Therefore, if we have the antiderivative of a function, we can use the derivative to find an equivalent formula without an integral.
In this case, the derivative of the antiderivative of f(t) = 4 - 2t is f(t) = 4 - 2t, which is the original function. So, the equivalent formula for A(x) is A(x) = 2x - 2x^2 + 4x - 4, which does not involve integrals.
Learn more about Integrals:
https://brainly.com/question/22008756
#SPJ4
can someone help me pretty pls

Answers
Answer:
Left to right: Zoe, Johana, Kami, Craig
Step-by-step explanation:
The values of x can be found by solving each of the equations.
A) x/-12 -2 = -22 ⇒ x = -12(-22 +2) = 240 . . . (first step: add 2)
B) 3x -21 = 15 ⇒ x = (15 +21)/3 = 12
C) -12x +2 = -22 ⇒ x = (-22 -2)/-12 = 2 . . . (first step: subtract 2)
D) 1/2x +66 = 126 ⇒ x = 2(126 -66) = 120
__
Zoe's equation requires adding 2 as the first step. It is equation A.
Craig's equation's solution is half that of Zoe's. 240/2 = 120. Craig's is equation D.
Kami's equation requires subtracting 2 as the first step. It is equation C.
Johana's equation's solution is 6 times that of Kami's. 6·2 = 12. Johana's is equation B.
The names that go in the blanks, left-to-right, are ...
Zoe, Johana, Kami, Craig
The number line below shows information
about a variable, m.
Select all of the following values that m
could take:
-2, 4, -3.5, 0, -5, -7
-5 -4 -3 -2 -1 0 1 2 3 4 5
m
Answers
From the given number line, the variable "m" could take the values of -2, -3.5, 0, and -5
To determine which values the variable "m" could take from the given number line, we need to identify the points or intervals on the number line that correspond to the possible values of "m".
Looking at the number line, we can see the following values:
-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5
From this list, the values that "m" could take are:
-2, -3.5, 0, -5
These values are present on the number line, indicating that they are possible values for "m".
Therefore, the variable "m" could take the values -2, -3.5, 0, and -5 from the given number line.
It's important to note that the values -7 and 4 are not present on the number line, so they are not possible values for "m" based on the information provided.
Know more about variable here:
https://brainly.com/question/28248724
#SPJ8
Eat For 10 Hours. Fast For 14. This Daily Habit Prompts Weight Loss, Study Finds This is the title of an NPR article about a 2019 study that recruited 19 overweight adults diagnosed with metabolic syndrome (elevated blood sugar, elevated cholesterol levels, high blood pressure). Participants were asked to restrict any eating to a period of just 10 hours each day. The study found a statistically significant reduction in body weight after 12 weeks of this eating pattern.
Define the parameter in this hypothesis test as a sentence in context.
Answers
Answer:
Step-by-step explanation:
The parameter in this hypothesis test describes the entire population. So in this test, the parameter is looking into the summary number for instance like an average of all overweights who after undergoing this pattern/daily habits exhibits weight loss.
Assume that adults have IQ scores that are normally distributed with a mean of μ=105 and a standard deviation σ=20. Find the probability that a randomly selected adult has an IQ between 93 and 117.
Answers
The probability that a randomly selected adult has an IQ between 93 and 117 is approximately 0.6827 or 68.27%.
What is probability?
Probability is a branch of mathematics that deals with the study of random events and their outcomes. It is the measure of the likelihood of an event occurring, expressed as a number between 0 and 1.
To find the probability that a randomly selected adult has an IQ between 93 and 117, we need to standardize the distribution using the z-score formula, and then find the area under the normal distribution curve between those two z-scores.
The z-score formula is:
z = (x - μ) / σ
where x is the IQ score we are interested in, μ is the mean IQ score, and σ is the standard deviation of IQ scores.
For the lower bound of 93, the z-score is:
z = (93 - 105) / 20 = -0.6
For the upper bound of 117, the z-score is:
z = (117 - 105) / 20 = 0.6
Now, we need to find the area under the normal distribution curve between these two z-scores. We can use a standard normal distribution table or a calculator to find this probability. Using a calculator, we can use the normalcdf function:
normalcdf(-0.6, 0.6, 0, 1)
This gives us a probability of 0.6827.
Therefore, the probability that a randomly selected adult has an IQ between 93 and 117 is approximately 0.6827 or 68.27%.
To learn more about probability visit:
https://brainly.com/question/24756209
#SPJ1
WELLPPPPPPPPPPP!!!! I NEED HELP ASAP

Answers
Answer:
Only B I'm pretty sure and if I'm wrong I'm sorry but I'm like 99% sure it's only B
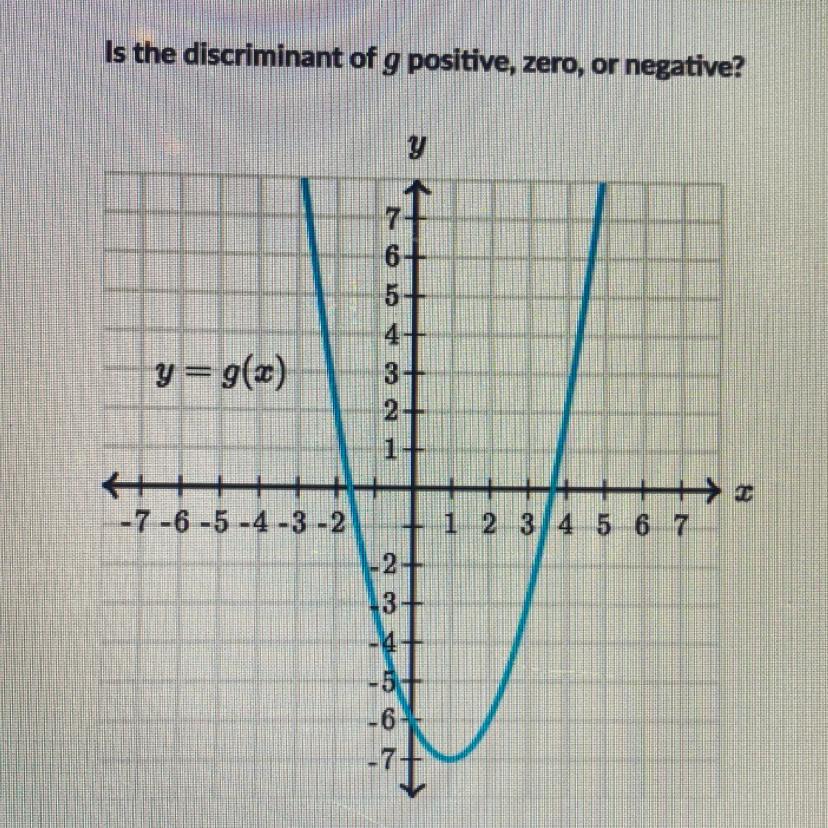
Is the discriminant of g positive, zero, or negative?
Answers
Answer:
the discriminant of g positive
Step-by-step explanation:
the discriminant of g positive because the graph of g cross the x-axis in two points.
A rain gutter is made from sheets of
aluminum that are 24 inches wide by
turning up the edges to form right
angles. Determine the depth of the
gutter that will maximize its cross-
sectional area and allow the greatest
amount of water to flow. What is the
maximum cross-sectional area?
Flat sheet 24 inches wide
1 Write a quadratic function for the Area in terms of x: A(x) =
2 The cross-sectional area is maximized when the depth of the gutter is
3 The maximum cross-sectional area is square inches.
Answers
1. The quadratic function for the Area in terms of x: A(x) = 24x.
2. The cross-sectional area is maximized when the depth of the gutter is 0.
3. The maximum cross-sectional area is square inches 0.
To determine the depth of the gutter that maximizes its cross-sectional area and allows the greatest amount of water to flow, we need to follow a step-by-step process.
1. Write a quadratic function for the area in terms of x:
The cross-sectional area of the gutter can be represented as a rectangle with a width of 24 inches and a depth of x. Therefore, the area, A(x), is given by A(x) = 24x.
2. The cross-sectional area is maximized when the depth of the gutter is:
To find the value of x that maximizes the area, we need to find the vertex of the quadratic function. The vertex of a quadratic function in form f(x) = ax² + bx + c is given by x = -b/(2a). In our case, a = 0 (since there is no x² term), b = 24, and c = 0. Thus, the depth of the gutter that maximizes the area is x = -24/(2 * 0) = 0.
3. The maximum cross-sectional area is square inches:
Substituting the value of x = 0 into the quadratic function A(x) = 24x, we get A(0) = 24 * 0 = 0. Therefore, the maximum cross-sectional area is 0 square inches.
Know more about the quadratic function here:
https://brainly.com/question/1214333
#SPJ8
Casey is driving from Portland to Sacramento at a rate of 70 miles per hour. The distance is 580 miles. how long will the trip take?
Answers
Answer: The trip will take 8.3 hours
Explanation:
The formula for calculating time is expressed as
time = distance/speed
From the information given,
distance = 580
speed = 70
Thus,
Time = 580/70
Time = 8.3 hours
I’m really stuck on this. PLEASE help

Answers
Answer:
34ft
Step-by-step explanation:
just add all of the numbers up
Because if you multiply all the side lengths and then divide by 2 that’s what you would get because you multiply in area and add in perimeter
For the graph given, select the statement that best represents the given system of equations.6x + 4y = 2 3x + 2y = 1
A. inconsistent
B. consistent and independent
C. not enough information
D. coincident
Answers
Answer:
D. coincidentStep-by-step explanation:
An coincident system of equations means that it has infinite solutions, because one line is on the other one. This happens when their equation are the same, or their "parent" line is the same.
So, given equations are:
6x + 4y = 2 and 3x + 2y = 1
Observe that if we divide the first by 2, we have
\(\frac{6x+4y}{2} =\frac{2}{2}\)
\(\frac{6x}{2}+\frac{4y}{2} =1\)
\(3x+2y=1\)
As you can see, using the first equation, we found that it has the same "parent" equation than the second equation. In other words, they are basically the same. This means that they represent the same line, so, the system is coincident and they have infinite solutions.
The answer is coincident :)
Solve cos 0 = 1 for 0, where 0º = 0 < 90°.
A) 60°
B) 0°
C)90
D)30
Answers
Answer:
to you in 1980 is the lol in lol1234in lol to you in the kids in the lero girl
Identify which line the error is in (1 point)
• Describe the error that was made (1 point)
State what the correct answer should be

Answers
Answer:
Step-by-step explanation:

Can someone help me please it's only 2 questions!!!!!


Answers
Problem 1
Answer: -4 + 7Reason: We start at 0 and move 4 units left. This is represented by 0+(-4) or 0-4. That simplifies to -4. Then add on 7 to move 7 units to the right to arrive at 3 as the final destination.
=============================================
Problem 2
Answer: 8 + 3Reason: We start at 0 and move 8 units to the right. That is represented by +8 or simply 8. Then the +3 will move us 3 more units to the right to get to 11 on the number line. This is one visual way to see why 8+3 = 11.
Please help meeeeeeeeeee

Answers
Answer:
A
Hope this helps
Step-by-step explanation:
Answer:
a
Step-by-step explanation:
Following y=mx+c
Gradient=-1/2
Y-intercept=-2
y=-1/2x-2
each function
f(x)=-4x-5;
ion for
Find ƒ(1)
for the given
Answers
When x is equal to 1, the Function f(x) = -4x - 5 yields a value of -9.
The find ƒ(1) for the function f(x) = -4x - 5, we need to substitute x = 1 into the function and evaluate the expression.
Replacing x with 1, we have:
ƒ(1) = -4(1) - 5
Simplifying further:
ƒ(1) = -4 - 5
ƒ(1) = -9
Therefore, when x is equal to 1, the value of the function f(x) = -4x - 5 is ƒ(1) = -9.
Let's break down the steps taken to arrive at the solution:
1. Start with the function f(x) = -4x - 5.
2. Replace x with 1 in the function.
3. Evaluate the expression by performing the necessary operations.
4. Simplify the expression to obtain the final result.
In this case, substituting x = 1 into the function f(x) = -4x - 5 gives us ƒ(1) = -9 as the output.
It is essential to note that the notation ƒ(1) represents the value of the function ƒ(x) when x is equal to 1. It signifies evaluating the function at a specific input value, which, in this case, is 1.
Thus, when x is equal to 1, the function f(x) = -4x - 5 yields a value of -9.
For more questions on Function .
https://brainly.com/question/11624077
#SPJ8
I need help asap please!!!

Answers
The values of the angles given are: 0,90,180,240,270,360,420,480,540,600,630,660,720 and
What is sine of angles?he sine of an angle is the trigonometric ratio of the opposite side to the hypotenuse of a right triangle containing that angle. It is defined as the length of the opposite side divided by the length of the hypotenuse
The given angles are: 0,30,45,90,120,135,180,210,225,240,270,300,315,330,360
2∅ 2*∅ = 0, 90,180,240,270,360,420,480,540,600,630,660,720
sin 2∅ = sin0 = 0; Sin90=1; sin180=0; sin240= -0.8660; sin270 = -1;
Each angle is multiplied by sine sine360 =1; sin420 = 0.8660; sin480= 0.9848; sin540=1; sin600=-0.8660; sin630=-1; sin660=0.8660; sin720= 0.9397
Learn more about sine of angles on https://brainly.com/question/22649800
#SPJ1
Solve the equation by completing the square. Round to the nearest hundredth if necessary. x2 – 4x = 5
Answers
The solution to x^2 - 4x = 5 is x = -1 or 5
How to solve the equation?The equation is given as:
x^2 - 4x = 5
Take the coefficient of x
k = -4
Divide by 2
k/2 = -2
Square both sides
(k/2)^2 = 4
Add this value to the sides of the equation
x^2 - 4x + 4= 5 + 4
Express as a difference of two squares
(x - 2)^2 = 9
Take the square root of both sides
x - 2 = ±3
Add 2 to both sides
x = 2 ± 3
Evaluate
x = -1 or 5
Hence, the solution to x^2 - 4x = 5 is x = -1 or 5
Read more about quadratic equations at:
https://brainly.com/question/10449635
#SPJ1
An report describes a survey of 251 adult Americans. Participants in the survey were asked how often they change the sheets on their bed and were asked to respond with one of the following categories: more than once a week, once a week, every other week, every three weeks, or less often than every three weeks. For this group, 11% responded more than once a week, 51% responded once a week, 26% responded every other week, 5% responded every three weeks, and 7% responded less often than every three weeks.
(a) Use the given information to make a relative frequency distribution for the responses to the question. How Often? Relative frequency
More than once a week Once a week Every other week Every three weeks Less often than
every three weeks
Answers
More than once a week: 0.11
Once a week: 0.51
Every other week: 0.26
Every three weeks: 0.05
Less often than every three weeks: 0.07
Relative Frequency Survey ResultsTo make a relative frequency distribution, follow these steps:
Count the number of occurrences of each category in the data. In this case, 11% of the 251 participants responded "more than once a week", so the number of occurrences for this category is 0.11 * 251 = 27.61 (rounded to 28). Similarly, 51% of the participants responded "once a week", so the number of occurrences for this category is 0.51 * 251 = 127.51 (rounded to 128). And so on for the other categories.
Divide the number of occurrences for each category by the total number of participants. In this case, the total number of participants is 251, so the relative frequency for "more than once a week" is 28 / 251 = 0.11. The relative frequency for "once a week" is 128 / 251 = 0.51. And so on for the other categories.
And that's it! These are the relative frequencies for each category in the data.
Learn more about Relative Frequency Survey Results here:
https://brainly.com/question/29706076
#SPJ4
if you toss a die once, consider the two events , you get a 5 OR 6. YOU GET AT MOST 3. are these events independent, explain WHY OR WHY NOT
Answers
Answer: These events are independent.
Step-by-step explanation:
Two events are considered independent if the outcome of one event does not affect the outcome of the other event. In this case, getting a 5 or 6 on a dice toss and getting at most 3 on a dice toss are independent events.
This is because the probability of getting a 5 or 6 is 2/6 or 1/3, which is completely unrelated to the probability of getting at most 3, which is 3/6 or 1/2. The outcome of getting a 5 or 6 does not affect the probability of getting at most 3, and vice versa. Therefore, these events are independent.
Question 2 Fill-In-The-Blank Worth 3 points)
(04.04)
Point R is at (4.1.5) and Point T is at (429) on a coordinate grid. The distance between the two points is_(Input numbers and decimal point only, such as 82)
Answer for Blank 1
Answers
Answer:
1.4
Step-by-step explanation:
in the graph, the points are 14 points apart, when the step of the graph is set to .1, if you count, they're .14 point apart, or 1.4
