HELP PLEASE! 11. Is the set of integers closed under division? Explain why or why not.
If it is not closed, give an example.

Answers
First a definition:
A given set is closed under a given operation if, for any given pair of elements of the set under that operation, the outcome also belongs to the set.
With this, we will find that the set of integer numbers is not closed under division.
Now let's be more clear.
The definition particularly means that a set is closed under division only if for any pair of elements of the set, the division of these elements also does belong to the set.
Here we want to see if the set of integers is closed under division. To see that this is false, we just need to find a counterexample.
This is, finding a pair of integer numbers that have a quotient that is not an integer.
A really simple example is:
1 and 2.
2/1 = 2 is integer.
but
1/2 = 0.5 is not integer.
Thus we can conclude that the set of integers is not closed under division.
If you want to learn more, you can read:
https://brainly.com/question/17175273
Related Questions
The graph shows the number of meters Jacob runs as a function of time in minutes.
If Sam runs 15 meters less each minute than Jacob does, which equation represents the total meters, m, that Sam runs in t minutes?
m = 200t
m = 185t
m = 215t
m = 15t

Answers
Answer:
its m=185t
Step-by-step explanation:
because if you divide
An equation which represent the total meters (m) that Sam runs in t minutes is: B. m = 185t.
How to determine the required equation?Mathematically, a proportional relationship can be represented with the following equation or mathematical expression:
m = kt
Where:
t represents the number of minutes.m represents the number of meters.k represents the constant of proportionality.Next, we would determine the constant of proportionality (k) for each candy as follows:
From Jacob's running, we have the following:
Constant of proportionality (k) = t/m
Constant of proportionality (k) = 400/2
Constant of proportionality (k) = 200
Since Sam runs 15 meters less each minute than Jacob does, an equation that represent the total meters (m) that he runs in t minutes is given by:
m = (200 - 15)t
m = 185t
Read more on proportionality here: brainly.com/question/12866878
#SPJ1
how many ft is equal to 1.66m
Answers
Answer:
5.44 meters
Step-by-step explanation:
We Know
0.3048 meter = 1 ft
How many ft makes a height of 1.66m?
We Take
1.66 ÷ 0.3048 ≈ 5.44 meters
So, the answer is 5.44 meters.
Question 19 of 25
Does this graph show a function? Explain how you know.
O A. No; the graph fails the vertical line test.
OB. Yes, the graph passes the vertical line test.
O C. Yes, there are no y-values that have more than one x-value.
OD. No; there are y-values that have more than one x-value.

Answers
A graph may or may not represent a function.
The true statement is: (b) Yes, the graph passes the vertical line test.
The vertical line test is used to determine if a graph represents a function or not.
When a vertical line is drawn through the graph, the line would only intersect with the curve at a point.
This means that:
The graph represents a function.
Hence, option (b) is true
Read more about functions and vertical line tests at:
https://brainly.com/question/17081515
I need help with this

Answers
Answer:
-3,1
Step-by-step explanation:
4(x-1)=3(x+3)
4x-4=3x+9
x=13
Denominator of a fraction cannot be zero. If it’s a zero the answerwill be undefined.
Therefore :
X-1 cannot be 0
Xcannot be 1
X+3 cannot be 0
X cannot be -3
) Quantifier negation.
Form the negation of the following statements. Then apply De Morgan’s law and/or conditional law, when
applicable. Negation should appear only within predicates, i.e., no negation should be outside a quantifier
or an expression involving logical connectives. Show all steps.
a) ∀x (P(x) ∧ R(x))
b) ∀y∃z(¬P(y) → Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Answers
The negations of the given statements with the application of De Morgan's law and/or conditional law.
a) ∃x (¬P(x) ∨ ¬R(x))
De Morgan's law:
∃y ∀z(¬P(y) ∧ ¬Q(z))
b) ∃y ∀z(¬P(y) ∧ ¬Q(z))
The double negation:
∃y ¬∃z(P(y) ∨ Q(z))
c) ¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
The conditional law:
¬∃x (P(x) ∨ (∀z (¬R(z)) → (∀z ¬Q(z))))
Let's form the negation of the given statements and apply De Morgan's law and/or conditional law, when applicable:
a) ∀x (P(x) ∧ R(x))
The negation of this statement is:
∃x ¬(P(x) ∧ R(x))
Now let's apply De Morgan's law:
∃x (¬P(x) ∨ ¬R(x))
b) ∀y∃z(¬P(y) → Q(z))
The negation of this statement is:
∃y ¬∃z(¬P(y) → Q(z))
Using the conditional law, we can rewrite the negation as:
∃y ¬∃z(¬¬P(y) ∨ Q(z))
c) ∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
The negation of this statement is:
¬∃x (P(x) ∨ (∀z (¬R(z) → ¬Q(z))))
Using the conditional law, we can rewrite the negation as:
¬∃x (P(x) ∨ (∀z (R(z) ∨ ¬Q(z))))
Applying De Morgan's law:
¬∃x (P(x) ∨ (∀z ¬(¬R(z) ∧ Q(z))))
Simplifying the double negation:
¬∃x (P(x) ∨ (∀z ¬(R(z) ∧ Q(z))))
Using De Morgan's law again:
¬∃x (P(x) ∨ (∀z (¬R(z) ∨ ¬Q(z))))
For similar questions on De Morgan's law
https://brainly.com/question/28735989
#SPJ8
What is the maximum number of intersection points two triangles can have, where no two sides are parallel? urgent please
Answers
Answer:
6
Step-by-step explanation:
Each side can, with a shape consisting of only convex angles (which triangles and squares by definition do) make at most two intersections.
Intersection point is the point at which the two lines are intersect each other.
The maximum number of intersection points two triangles can have, where no two sides are parallel is 6.
What is intersection point?
Intersection point is the point at which the two lines are intersect each other.
Given-
Two triangle intersect each other.
Number of parallel lines for the two triangle is zero.
Two triangle can intersect each other at number of ways.
If any side of two triangle is not parallel then they cuts each other as shown in the given figure to obtained the maximum number of intersection.
As the one side (line) of the one triangle can cut the other triangle only two times ( if vertex is not considered). Thus the number of time total 3 sides of a triangle cuts the other triangle is,
\(=2\times3\\=6\)
Hence, the maximum number of intersection points two triangles can have, where no two sides are parallel is 6.
Learn more about the intersect point of triangle here;
https://brainly.com/question/26179054

Help me ASAP plssssssssssssssssssssssssssssssss

Answers
Answer:
C
Step-by-step explanation:
Will someone please answer these problems?? I need them done ASAP!!!!!!


Answers
Answer:
Step-by-step explanation:
1. 10/15 = 2/3. Similar.
2. 101/151 ≠ 100/150. Not similar.
3. 10/20 = 7/14 = 4/8. Similar
4. 6/3 = 7/3.5 = 7/3.5 Similar
A tank contains 22 gallons of water when all of a sudden the water begins draining at a constant rate of 2 gallons per hour. Let t represent the number of hours since the water began draining and let v represent the volume of water in the tank. a. Write a formula that expresses v in terms of t
b. As t increases from 3 to 5, v varies from___ to ____
c. As t varies from 3 to 5, how much do t and v change by?
Answers
a). The formula that expresses v in terms of t is v = 22 - 2t, b). As t increases from 3 to 5, v varies from 16 to 12, c). As t varies from 3 to 5, v changes by 16 - 12 = 4.
What is the volume?
'Volume' is a mathematical quantity that shows the amount of three-dimensional space occupied by an object or a closed surface. The unit of volume is in cubic units such as m3, cm3, in3, etc. Sometimes, volume is also termed capacity.
a). The volume of water in the tank, v, decreases by 2 gallons per hour, so the formula for v in terms of t is v = 22 - 2t.
b). As t increases from 3 to 5, v varies from 16 to 12. That is, as t goes from 3 to 5, v decreases from 22 - 2(3) = 16 to 22 - 2(5) = 12.
c). As t varies from 3 to 5, t changes by 5 - 3 = 2, and v changes by 16 - 12 = 4.
Hence, a). The formula that expresses v in terms of t is v = 22 - 2t, b). As t increases from 3 to 5, v varies from 16 to 12, c). As t varies from 3 to 5, v changes by 16 - 12 = 4.
To learn more about the volume visit,
https://brainly.com/question/12410983
#SPJ4
Negative numbers do not have square roots that are real numbers
Answers
Answer:
Negative numbers don't have real square roots since a square is either positive or 0. The square roots of numbers that are not a perfect square are members of the irrational numbers. This means that they can't be written as the quotient of two integers.
Summary
Give an example of a proportional relationship and write an equation that represents the relationship.
Answers
The proportional relationship is represented by the formula, y = kx, which demonstrates that y increases at the same rate as x does
Relationships between two variables that are proportional occur when their ratios are equal.
Another way to consider them is that in a proportionate relationship, one variable is consistently equal to the other's constant value. The "constant of proportionality" is the name of this constant.The ratio of the constant values of two proportional quantities is known as the proportionality constant.When either the ratio or product of two changing values results in a constant, that pair of values is said to be in proportion.The Direct Variation and Inverse Variation types of proportions between the two provided values determine the value of the proportionality constant.The direct proportionality formula, y = kx, demonstrates that y increases at the same rate as x does. The cost per item (y), which is inversely proportional to the number of things purchased (x), is represented by the symbol y x.By using the indirect proportionality formula, y = k/x, it can be seen that when y rises, x falls, and vice versa.Therefore the proportional relationship is represented by the formula,
y = kx .
To learn more about proportional relationship visit:
https://brainly.com/question/12917806
#SPJ1
a- bx = c – dx; 5 – 3x = 1 – 4x
Need help
Answers
Answer:
there's a site called cymath you can put equations there and it answers almost all equations
Step-by-step explanation:
Given rhombus QRST, find the
perimeter if QU = 3 and RU equals 4.
Q
R
T
U
X
S

Answers
The perimeter of the rhombus in this problem is given as follows:
19.8 units.
What is the perimeter of a polygon?The perimeter of a polygon is given by the sum of all the lengths of the outer edges of the figure, that is, we must find the length of all the edges of the polygon, and then add these lengths to obtain the perimeter.
The diagonal length can be obtained as follows:
QU = US = 3.RU = UT = 4.RU + UT = 7.
Applying the Pythagorean Theorem, the side length is obtained as follows:
x² + x² = 7²
2x² = 49
\(x = \sqrt{\frac{49}{2}}\)
x = 4.95.
Then the perimeter is given as follows:
P = 4 x 4.95
P = 19.8 units.
More can be learned about the perimeter of a polygon at https://brainly.com/question/3310006
#SPJ1
Annette has 3 hours to spend training for an upcoming race. She completes her training by running full speed the distance of the race and walking back the same distance to cool down. If she runs at a speed of 9mph and walks back at a speed of 3mph , how long should she plan to spend walking back?
Answers
Answer:
Annette should plan to spend 2.25 hours walking back.
Step-by-step explanation:
To solve this problem, we can use the formula:
Time = Distance / Speed
Let's assume the distance of the race is D miles.
Annette spends her time running the distance of the race, which takes:
Time running = D / 9 hours
She then walks back the same distance, which we need to find the time for:
Time walking = D / 3 hours
Since Annette has a total of 3 hours for her training, the sum of the running time and walking time should equal 3 hours:
D / 9 + D / 3 = 3
To simplify the equation, we can multiply all terms by 9 to eliminate the denominators:
D + 3D = 27
Combining like terms:
4D = 27
Dividing both sides of the equation by 4:
D = 6.75
So, the distance of the race is 6.75 miles.
To find the time Annette should spend walking back, we substitute the distance into the time-walking formula:
Time walking = D / 3 = 6.75 / 3 = 2.25 hours
Therefore, Annette should plan to spend 2.25 hours walking back.
The fundamental frequency of a certain 64.5 cm string is 352 Hz. Based on this information, what is the velocity of the wave traveling in this string?
1. 454 m/s
2. 343 m/s
3. 119 m/s
4.
227 m/s
Answers
Answer:
3. 119 m/s
Step-by-step explanation:
Which decimal number and fraction are equivalent?
A. 0.27 and
27/40
B. 0.35 and
7/20
C. 0.58 and
12/25
D. 0.64 and
4/5
Answers
Answer:
B
Step-by-step explanation:
If you convert 0.35 is equal to 7/20
use the simple interest formula (I = prt) to solve for the missing value in the following situations
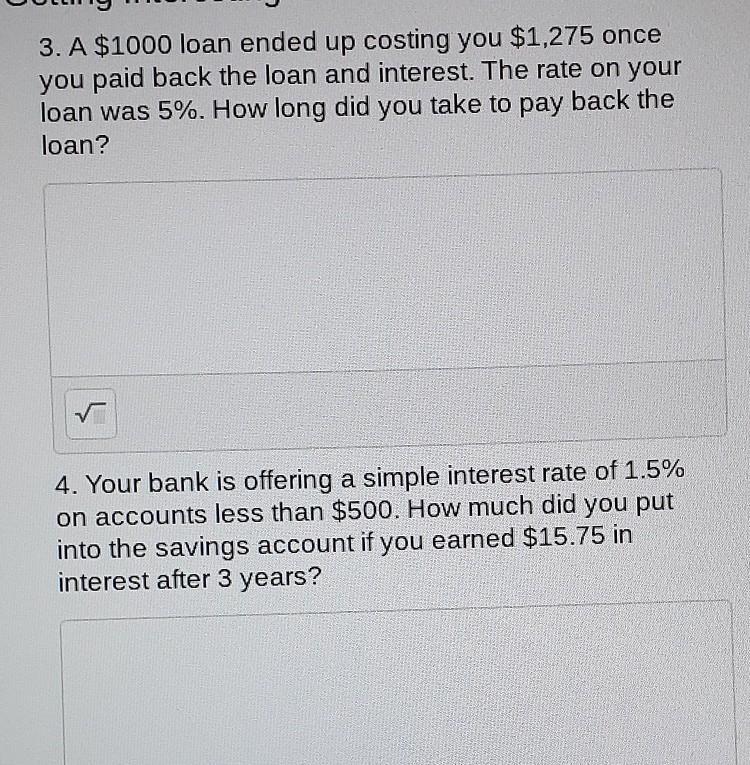
Answers
Formula I = prt
p = 1000
r = 5%
t = ?
1000 ----------------------100%
275 ----------------------- x
x = (275 x 100) / 1000
x = 27.5%
275 = (1000)(0.05) t
t = 275 / (1000 x 0.05)
t = 275 / 50
t = 5.5 years
2.- p = I/rt
p = 15.75/(0.015 x 3)
p = 15.75 / 0.045
p = 350
Initial amount of money = $350
An orchard charges $0.85 to ship a kilogram ofgrapefruit. Each grapefruit weighs approximately 165grams. How much will it cost to ship 40 grapefruits?
Answers
Answer:
$5.61
Explanation:
The approximate weight of each grapefruit = 165 grams
First, calculate the total weight of 40 grapefruits.
\(\begin{gathered} \text{Total Weight}=165\times40 \\ =6600\text{ grams} \\ =\frac{6600}{1000}kg \\ =6.6\operatorname{kg} \end{gathered}\)Since the orchard charges $0.85 to ship a kilogram of grapefruit, the cost of shipping 40 grapefruits will be:
\(\begin{gathered} C=0.85\times6.6 \\ =\$5.61 \end{gathered}\)Bob has a total of 60 adventure cards for a game. The table shows the number of cards, c, distributed to p players. Which equation describes the pattern in the table?
p 2 3 4 5
c 30 20 15 12
c = 60 ÷ p
c = 60 – p
c = 60p
c = 60 + p
Answers
For a game, Bob has a total of 60 adventure cards. The distribution of cards, c, to players, p, is shown in the table. c = 60 ÷ p
Describe probability. Describe using an example.Probability defines the possibility of occurrence of an event. Probability is the unit of measurement for an event's likelihood. It represents the proportion of positive results to all results. For instance: Receiving the numbers 3 and 5 while rolling the dice, as well as getting both an even and an odd number.
The equation would read: c = 60 / 2, which implies c = 30 if p=2. The equation would read 12 = 60 / p, p = 5, 20 = 60 / 3, etc. If c = 12, the equation would read... 12 = 60 / p, and p = 5, and so on, 20 = 60 / 3, and 15 = 60 / 4.
To know more about Table visit:
brainly.com/question/20648466
#SPJ1
cramer's rule is a method of calculating the solution to a system of linear equations by finding the of the determinants.
Answers
Cramer's rule is a method of calculating the solution to a system of linear equations by finding the "Quotient" of the determinants.
Hence, option (a) is correct choice.
Cramer's rule is one of the most significant strategies for solving a system of equations. The values of the system's variables are to be computed using determinants of matrices in this technique. As a result, Cramer's rule is frequently referred to as the determinant technique.
If unique solutions exist, this approach is utilized to find them. Cramer's rule cannot be used if the determinant of the coefficient matrix is zero.
To use Cramer's Rule to solve a system of three equations in three variables, substitute a variable column with the constant column for each desired solution: x=DxD, y=DyD, z=DzD.
For more questions on Cramer's rule
https://brainly.com/question/29274071
#SPJ4
The missing option be:
(a) Quotient
(b) Divisor
(c) Factor
(d) Multiple
Jerrica and her brother like to play chess. About a month ago they decided to keep track of how manygames they have won. As of today, Jerrica has won 20 out of the 35 games against her brother.
a. How many games would Jerrica have to win in a row in order to have an 80% winning record?
Justify your answer.
Answers
Jerrica would have to win 40 additional games in a row to have an 80% winning record. This would bring her total wins to 20 + 40 = 60, and her total games played to 35 + 40 = 75.
To determine how many games Jerrica would have to win in a row in order to have an 80% winning record, we need to calculate the number of games she needs to win out of a certain total.
Let's denote the number of games she needs to win in a row as x. If she wins x additional games, her total wins would be 20 + x, and her total games played would be 35 + x.
To have an 80% winning record, she would need to win 80% of the total games played. Mathematically, this can be expressed as:
(20 + x) / (35 + x) = 80 / 100
Cross-multiplying, we get:
100(20 + x) = 80(35 + x)
Expanding and simplifying:
2000 + 100x = 2800 + 80x
Subtracting 80x from both sides:
20x = 800
Dividing by 20:
x = 40
Jerrica would have to win 40 additional games in a row to have an 80% winning record. This would bring her total wins to 20 + 40 = 60, and her total games played to 35 + 40 = 75.
For more such questions on total wins
https://brainly.com/question/29165018
#SPJ8
-4 is greater than of equal to x - 11
Answers
Using the inequality rule we know that 11 is greater than -11, (11 > -11).
What is an Inequality Equation?Mathematical expressions with inequalities are those in which the two sides are not equal.
Contrary to equations, we compare two values in inequality.
Less than (or less than or equal to), greater than (or greater than or equal to), or not equal to signs are used in place of the equal sign.
Two expressions in inequality aren't always equal, which is denoted by the symbols >, <, ≤, or ≥.
So, let's say the inequality equation looks like this: A
Right now, A is valued at
Let p be used to representing the initial number.
P equals 11, so
Let q be used to representing the second number.
Q has a value of -11.
-11 and 11 are both numbers that are greater than zero.
Then, 11 > -11 ... (1)
A has a value of 11 > -11.
Therefore, using the inequality rule we know that 11 is greater than -11, (11 > -11).
Know more about Inequality here:
brainly.com/question/11897796
#SPJ1
Correct question:
Is 11 greater than, equal to, or less than -11?
Solve for x and explain your steps in detail using the R-E-S-T Method
8x - 4 = 92
Answers
Answer:
12
Step-by-step explanation:
you add 92 with the 4 and get 96 then you divide the 8x with the 96 and get 12
Hope it helps <333
x = 12
Calculations ↓Our goal is to find the value of x .
To find the value of x we need to get x by itself .
The first step is to move all numbers to the right . Luckily , there's only one number here : 4.
So we add 4 on both sides :
8x=96
Now divide by 8 on both sides :
x = 12
So the value of x is 12.\(\footnotesize\text{hope\:helpful~}\)
Consider the expression below. Assume the variable m represents an integer. 6m(3m + 21) Enter an expression in the box that uses the variable m and makes the equation true. (Simplify your answer completely. If no expression exists, enter DNE.) 6m(3m + 21) = 9 Given that m represents an integer, is 6m(3m + 21) divisible by 9?
Answers
Answer:
\((a)\ 6m(3m + 21) = 9(2m^2 + 14m)\)
(b) Yes, it is divisible by 9
Step-by-step explanation:
Given
\(6m(3m + 21)\)
Solving (a): Complete the blanks
\(6m(3m + 21) = 9 [\ ]\)
Expand the bracket
\(6m(3[m + 7]) = 9 [\ ]\)
\(6m*3(m + 7) = 9 [\ ]\)
Express 6m as 2m * 3
\(2m*3*3(m + 7) = 9 [\ ]\)
\(2m*9(m + 7) = 9 [\ ]\)
Rewrite as:
\(9 * 2m(m + 7) = 9 [\ ]\)
Multiply the bracket by 2m
\(9 * (2m^2 + 14m) = 9 [\ ]\)
Divide both sides by 9
\(2m^2 + 14m = [\ ]\)
Hence, the bracket will be filled with: \(2m^2 + 14m\)
So:
\(6m(3m + 21) = 9(2m^2 + 14m)\)
Solving (b): Is \(6m(3m + 21)\) divisible by 9?
In (a), we have:
\(6m(3m + 21) = 9(2m^2 + 14m)\)
The leading factor "9" implies that the expression is divisible by 9
Select the correct answer.
Which statement is true?
OA
Point estimates are used to make inferences about population parameters.
OB. When we use the population mean and proportion to summarize information about the entire population, we call them point
estimates.
OC. The population mean and proportion are always equal to their corresponding point estimates.
O D.
The sample mean and sample proportion of a population are called population parameters.
Answers
Answer:
A. Point estimates are used to make inferences about population parameters.
What is the line’s slope?

Answers
Answer:
slope = - \(\frac{1}{4}\)
Step-by-step explanation:
Calculate the slope m using the slope formula
m = \(\frac{y_{2}-y_{1} }{x_{2}-x_{1} }\)
with (x₁, y₁ ) = (- 4, 0) and (x₂, y₂ ) = (0, - 1) ← 2 points on the line
m = \(\frac{-1-0}{0-(-4)}\) = \(\frac{-1}{0+4}\) = \(\frac{-1}{4}\) = - \(\frac{1}{4}\)
Please help !!!!!! 20 points

Answers
The value of x in the polygon will be 13.25 degrees.
The value of x is 10.
We can find the value of x by plugging in the number of sides of the regular polygon into the formula x = (n-2)*15° - 1.
How to calculate the valueThe sum of the interior angles of a regular polygon with n sides is (n-2) x 180 degrees.
Sum of angles = (24-2) x 180 = 22 x 180 = 3960 degrees
Since all the angles in a regular polygon are congruent, we can divide the sum of the angles by the number of angles to find the measure of one angle:
Measure of one angle = 3960/24 = 165 degrees
165 = 12x + 6
159 = 12x
x = 13.25
Therefore, the value of x is 13.25 degrees.
Each of the triangles in our decomposition has one angle equal to (17x+2)°, so the sum of all the angles in the triangles is 43 × (17x+2)° = 731x+86°.
Therefore, we have:
731x+86° = 7380°
Solving for x, we get:
731x = 7294°
x = 10
Therefore, the value of x is 10.
The equation that can be used to find the value of x is:
(9x+48)° + (15x-24)° = (n-2)*180°
24x + 24 = (n-2)*180°
Dividing both sides by 24, we get:
x + 1 = (n-2)*15°
Subtracting 1 from both sides, we get:
x = (n-2)*15° - 1
Learn more about polygon on
https://brainly.com/question/1592456
#SPJ1
In ADEF, f= 33 inches, ZF=140° and ZD=5°. Find the length of e, to the nearest 10th
of an inch.
Answers
The length of e is 29.53 inches.
what is Sine Law?In the following, the law of sine is presented in detail: In a triangle, the sine of angle A divided by side "a" equals the sine of angle B divided by side "b" equals the sine of angle C divided by side "c".
Given:
f= 33 inches
<F= 140, <D = 5
Now,
<E= 180 - (<F+ <D) = 180 - (140 + 5) = 35
Using Sine law
sin F / f = sin E/ e
sin 140 / 33 = sin 35 / e
0.642/ 33 = 0.573 / e
0.0194 e= 0.573
e= 29.53 inches
Hence, the length of e is 29.53 inches.
Learn more about sine law here:
https://brainly.com/question/17289163
#SPJ1
is this relation a function?

Answers
A good way to determine this is by using the vertical line test.
If m<7 is 2x + 30 and m<28 is 3x - 10, find the
following:

Answers
Answer:
x = 32
m∠7 = 94
m∠8 = 86
m∠3 = 94
Step-by-step explanation:
(2x + 30) + (3x - 10) = 180
5x + 20 = 180
5x = 160
x = 32
m∠7 = 2(32) + 30 = 94
m∠8 = 3(32) - 10 = 86
or
m∠8 = 180 - 94 = 86
m∠3 ≈ m∠7 (corresponding angles)