Answers
Answer:
2x+3=9
2x=6
x=3
3w-1=14
3w=15
w=5
7y+2=30
7y=28
y=4
5x+20=35
5x=15
x=3
6c-12=48
6c=60
c=10
8m-4=20
8m=24
m=3
7w+13=90
7w=77
w=11
12p-18=30
12p=48
p=4
9w-5=67
9w=72
w=8
10a+40=100
10a=60
a=6
9x-24=84
9x=108
x=12
7w+1=1
7w=0
w=0
your welcome
Answer:
The answers will be listed below:
A. \(x=3\)
B. \(w=5\)
C. \(y=4\)
D. \(x=3\)
E. \(c=10\)
F. \(m=3\)
G.\(w=11\)
H. \(p=4\)
I. \(w=8\)
J. \(a=6\)
K. \(x=12\)
L.\(w=0\)
I would show how to do it but it will take to long.
Here's for the last one
Hope this helps.

Related Questions
Find the length on the given race track

Answers
The length of the race track is 171m
How to determine the lengthTo determine the length of the race track, we need to know that the length takes the shape of a rectangle
Now, we have that the formula that is used for calculating the perimeter of a rectangle is expressed as;
P = 2(l +w)
Such that the parameters of the formula are;
P is the perimeterl is the lengthw is the widthSubstitute the values, we have;
Perimeter = 2(25.5 + 60)
expand the bracket, we get;
Perimeter = 2(85.5)
Perimeter = 171 m
Learn more about rectangles at: https://brainly.com/question/25292087
#SPJ1
The perimeter of a square is 24 m. find it's area
Answers
Answer:
A=36m²
Step-by-step explanation:
Using the formulas
A=a²
P=4a
Solving forA

2000:$5.00 2015:6.50 what is the change in the cost of the cheeseburger
Answers
New price - old price = difference
6.50 - 5.00 = 1.50
If you want per year, there were 5 years between prices so divide by 5:
1.50/5 = 0.30 per year. So 30 cents every year or $1.50 overall
What is the area of triangle abc if a = 12, b = 17, and C = 100°?
Answers
Area = (1/2) * base * height
where the base and height of the triangle can be any two sides of the triangle, as long as they form a right angle.
In this case, we are given the lengths of sides a and b, but we do not have the height of the triangle. However, we can use the law of sines to find the height:
sin(C) / c = sin(A) / a
sin(100°) / c = sin(A) / 12
Solving for sin(A), we get:
sin(A) = (12 * sin(100°)) / c
sin(A) = (12 * sin(100°)) / 17 (since c = b = 17)
sin(A) ≈ 0.7049
Now, we can use the formula for the area of a triangle:
Area = (1/2) * base * height
where base = a = 12 and height = b * sin(A) = 17 * sin(A):
Area = (1/2) * 12 * 17 * sin(A)
Area ≈ 103.5
Therefore, the area of triangle ABC is approximately 103.5 square units.
If y varies inversely as x and y = 5 when x = 10, find y when x = 2.
Answers

HELP MEEE PLEASE
Gilligan sees a ship coming close to the shore he's standing on. He wants to
determine the distance (SD) from the ship to the shore. He walks 130 ft along the
shore from point D to point C and marks that spot. Then he walks 23 ft further and
marks point B. He turns 90 and walks until his location (point A), point C, and point
S are collinear.
o
Answer the following questions making sure to show all your work.
(a) Can Gilligan conclude that triangle ABC and triangle SDC are similar? Why or why
not?
(b) Suppose AB = 90 ft. What can Gilligan conclude about the distance of the ship
from the shore? Explain.

Answers
The triangles ABC and SDC are similar triangles
Gilligan can conclude that triangles ABC and SDC are similarGilligan can conclude that the distance of the ship from the shore is 509 ftHow to determine if the triangles are similarFrom the question, we understand points S, C and A are collinear, while line AB and SD are vertical and parallel lines at the either sides of point C.
Hence, Gilligan can conclude that triangles ABC and SDC are similar
How to calculate the distance SD
To do this, we make use of the following equivalent ratio
\(SD : 130 = AB : 23\)
Substitute 90 for AB
\(SD : 130 =90 : 23\)
Express as fraction
\(\frac{SD}{130} =\frac{90}{ 23}\)
Make SD the subject
\(SD =\frac{90}{ 23} * 130\)
\(SD =509\)
Hence, Gilligan can conclude that the distance of the ship from the shore is 509 ft
Read more about similar triangles at:
https://brainly.com/question/14285697
9•10^7 is how many times as large as 3•10^7
Answers
Answer:
9*10^7 is 90000000. 3*10^7 is 30000000. So it is 3 times as large
Nicole, Justin, and Shen have a total of $85 in their wallets. Shen has 2 times what Justin has. Nicole has $9 more than Justin. How much does each have?
Answers
Answer:Nicole has $94, shen has $170 and justuin has $85
Step-by-step explanation:
85+9=94 85 times 2= 170
Answer:
Step-by-step explanation:
Justin has 19
Nicole has 28
Shen has 38
Drag the number to match each rate to its equivalent ratio

Answers
Answer:
To find the mpg all we have to do is divide the numbers in the ratio.
119 miles / 3.5 gallons = 34 mpg
77 mi / 2.2 gal = 35 mpg
153 mi / 4.25 gal = 36 mpg
plsss help
For the given polynomial, determine which of the binomials listed are factors. Pick two.
f(x) = 2x3 + 9x2 + 13x + 6
A.x + 1
B.x – 1
C.x + 2
D.x – 2
E.x + 3
F.x – 3
Answers
The factors for the Polynomial are (x+1) and (x+2).
What is Factor Theorem?According to factor theorem, if f(x) is a polynomial of degree n ≥ 1 and 'a' is any real number, then, (x-a) is a factor of f(x), if f(a)=0.
Given:
f(x) = 2x³ + 9x² + 13x + 6
Now, first (x+1) =0
x= -1
put x= -1 in f(x) as
f(-1) = 2(-1) + 9(1) + 13(-1) + 6
= -2 + 9 - 13 + 6
= 0
So, (x+1) is factor of f(x).
Now, second (x-1)= 0
x= 1
put x= 1 in f(x) as
f(1) = 2(1) + 9(1) + 13(1) + 6
= 2 + 9 + 13 + 6
= 31
So, (x-1) is not a factor of f(x).
Now, second (x+2)= 0
x= -2
put x= -2 in f(x) as
f(1) = 2(-2)³ + 9(-2)² + 13(-2) + 6
= -16 + 36 - 26 + 6
= 0
So, (x+2) is factor of f(x).
Now, second (x-2)= 0
x= 2
put x= 2 in f(x) as
f(1) = 2(2)³ + 9(2)² + 13(2) + 6
= 16 + 36 + 26 + 6
= 84
So, (x-2) is not a factor of f(x).
Now, second (x+3)= 0
x= -3
put x= -3 in f(x) as
f(1) = 2(-3)³ + 9(-3)² + 13(-3) + 6
= -54 + 81 - 39 + 6
= -6
So, (x+3) is not a factor of f(x).
Now, second (x-3)= 0
x= 3
put x= 3 in f(x) as
f(1) = 2(3)³ + 9(3)² + 13(3) + 6
= 54 + 81 + 39 + 6
= 180
So, (x-3) is not a factor of f(x).
Learn more about factor theorem here:
https://brainly.com/question/13547729
#SPJ1
solve the equation -8x-3(2x+1)=67
Answers
Answer:
=
−
5
Step-by-step explanation:
−
8
−
3
(
2
+
1
)
=
6
7
-8x{\color{#c92786}{-3(2x+1)}}=67
−8x−3(2x+1)=67
−
8
−
6
−
3
=
6
7
-8x{\color{#c92786}{-6x-3}}=67
−8x−6x−3=67
2
Combine like terms
−
8
−
6
−
3
=
6
7
{\color{#c92786}{-8x}}{\color{#c92786}{-6x}}-3=67
−8x−6x−3=67
−
1
4
−
3
=
6
7
{\color{#c92786}{-14x}}-3=67
−14x−3=67
3
Add
3
3
3
to both sides of the equation
−
1
4
−
3
=
6
7
-14x-3=67
−14x−3=67
−
1
4
−
3
+
3
=
6
7
+
3−
1
4
=
7
0
-14x=70
−14x=70
5
Divide both sides of the equation by the same term
−
1
4
=
7
0
-14x=70
−14x=70
−
1
4
−
1
4
=
7
0
−
1
4
\frac{-14x}{{\color{#c92786}{-14}}}=\frac{70}{{\color{#c92786}{-14}}}
−14−14x=−1470
6
Simplify
Cancel terms that are in both the numerator and denominator
Divide the numbers
=
−
5
-14x-3=67
-14x=70
-14/70
x=-5
i hope that helped
A straw is placed inside a rectangular box that is 2 inches by 1 inches by 3 inches, as shown. If the straw fits exactly into the box diagonally from the bottom left corner to the top right back corner, how long is the straw? Leave your answer in the simplest radical form.
Answers
The length of the straw is 3.74 inches.
What is mean by Rectangle?A rectangle is a two dimension figure with 4 sides, 4 corners and 4 right angles. The opposite sides of the rectangle are equal and parallel to each other.
Given that;
In rectangular box,
Length (l) = 2 inches
Width (w) = 1 inches
Height (h) = 3 inches
Here, The straw is said to fit into the box diagonally from the bottom.
So, the length (s) of the straw is calculated as:
⇒ s = √ l² + w² + h²
⇒ s = √ 2² + 1² + 3²
⇒ s = √ 4 + 1 + 9
⇒ s = √ 14
⇒ s = 3.74 inches
Thus, The length of straw = 3.74 inches
Learn more about the rectangle visit:
https://brainly.com/question/2607596
#SPJ1
The length of the straw will be 3.7416 inches long in radical form.
What is Length of diagonal in cuboid?If a cuboid has length = l units, breadth = b units, and height = h units, then we can evaluate the length of the diagonal of a cuboid using the formula : X²=l²+b²+h²
Here,
As per the question the length of the straw is equal to length of the diagonal of Rectangular box.
l= 3 inch , b= 2 inch , h= 1 inch
Let us consider the length of the straw be 'x'.
As, Diagonal of Cuboid is,
X²=14
X=√14
i.e. X=3.7416
We get, X= 3.7416 (in radical form)
Hence, the length of the straw will be 5.91607 inches.
Learn more about length of Diagonal here:
brainly.com/question/9740924
#SPJ1
Teresa has a clock that gives off a signal every 60 minutes, another clock that gives off a signal every 150 minutes, and a third one that gives off a signal every 360 minutes. At 9 am, all three clocks coincide and give off the signal at the same time. a) What is the least amount of hours it will take for the clocks to coincide again? b) At what time will they all give off the signal?
Answers
Answer:
\(\mathrm{Least\:Common\:Multiple\:of\:}60,\:360,\:150:\quad 1800\)
in 30 hours
Step-by-step explanation:
A triangle is placed in a semicircle with a radius of 3 mm, as shown below. Find the area of the shaded region.
Use the value 3.14 for π, and do not round your answer. Be sure to include the correct unit in your answer.
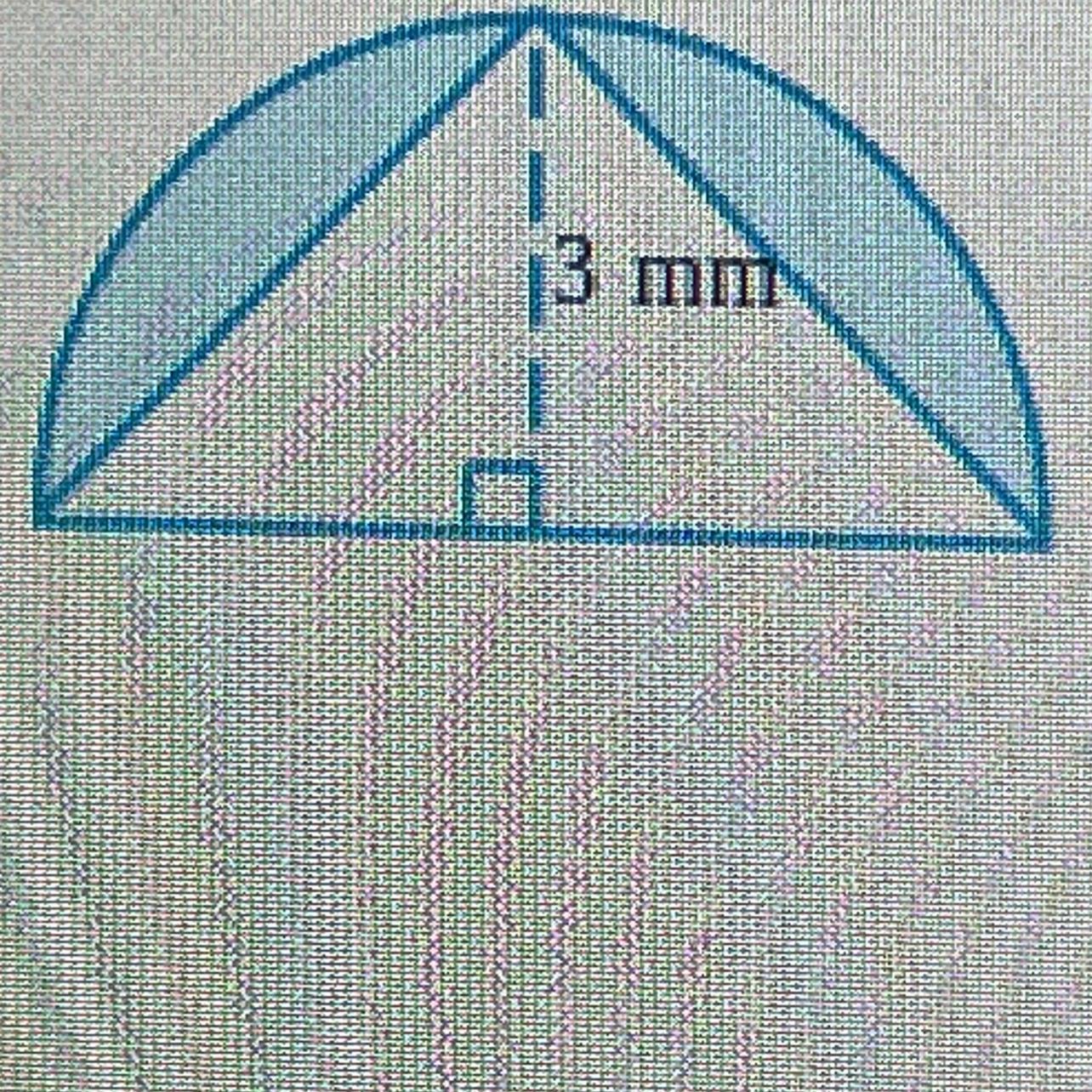
Answers
Answer:
The area of the shaded region is approximately 3 mm^2.
Step-by-step explanation:
To find the area of the shaded region, we need to find the area of the triangle and subtract the area of the circle that overlaps with the triangle. We know the radius of the semi-circle is 3mm, and therefore the radius of the whole circle is 6mm. We can use the formula A = 1/2 * base * height for the triangle, and the formula A = π * r^2 for the area of the circle.
Calculate the height of the triangle:
We can use the formula h = sqrt((9mm^2 - b^2) / 4), where h is the height of the triangle and b is the base of the triangle, to calculate the height of the triangle. Since the triangle is isosceles, we know that base = 3mm. Therefore, the height of the triangle is h = sqrt((9mm^2 - 3mm^2) / 4) = sqrt(12mm^2 / 4) = sqrt(3 mm).
2. Calculate the area of the triangle:
The area of the triangle is A = 1/2 * base * height = 1/2 * 3mm * sqrt(3 mm) = sqrt(3 mm) = 0.5389 mm^2.
3. Calculate the area of the overlapping region:
The circle that overlaps with the triangle has a diameter of 6mm. Therefore, its area is A = π * r^2, where r = radius = 3mm. Therefore, the area of the overlapping region is A = π * 3mm^2 = π * 0.09 mm^2.
4. Calculate the area of the shaded region:
The area of the shaded region is the area of the semicircle minus the area of the overlapping region. Therefore, the area of the shaded region is A = π * 6mm^2 - A = π * 6mm^2 - π * 0.09 mm^2 = 2.993 mm^2.
Therefore, the area of the shaded region is approximately 3 mm^2.
The Gala Restaurant uses the equation 30n - C + 200 = 0 to determine the cost for a room rental, where a represents the cost. in dollars, which depends on n. the number of people attending. Express the equation in slope y-intercept form: C = mn + b
Answers
Given:
The equation is:
\(30n-C+200=0\)
To find:
The slope intercept form of the given equation.
Solution:
We have,
\(30n-C+200=0\)
We need to write the given equation in the form of \(C=mn+b\).
Adding C on both sides, we get
\(30n-C+200+C=0+C\)
\(30n+200=C\)
Interchanging the sides, we get
\(C=30n+200\)
This equation is in the form of \(C=mn+b\), where m is 30 and b is 200.
Therefore, the slope intercept form of the given equation is \(30n-C+200=0\).
The measure of the minor arc BC is 63º. What is the measure of ZBAC?
Answers
Answer:
measure or arc BAC should be 297 degrees (with assumptions)
Step-by-step explanation:
Assumption 1: the cap Z in your question is actually an angle symbol
Assumption 2: A is the center of the circle
IF these assumptions are true, then the measure of arc BAC is 36 - 63 = 297 degrees
if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other. a) true b) false
Answers
The statement "if the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other" is true. The dot product of two vectors is zero if and only if the vectors are perpendicular.
The dot product of two vectors is defined as the product of their magnitudes and the cosine of the angle between them. When the dot product is zero, it means that the cosine of the angle between the vectors is zero, which occurs when the vectors are perpendicular.
In other words, the dot product being zero indicates that the vectors are at a 90-degree angle to each other, supporting the statement that they are perpendicular.
Learn more about dot product here: brainly.com/question/23477017
#SPJ11
The daily changes in the barometric pressure for four days are −0.05, 0.09, −0.04, and −0.08 inches. The mean change after five days is −0.01 inch. What is the change on the fifth day? Write your answer as a decimal.
Answers
The change on the fifth day is 0.03.
What is a mean?A mean simply means the average of.a set of numbers.
Based on the information given, let the change in the fifth day be x. This will be illustrated as:.
= (-0.05 + 0.09 - 0.04 - 0.08 + x)/ 5 = -0.01
Crops multiply
-0.08 + x = -0.05
Collect like terms
x = -0.05 + 0.08
x = 0.03
The change is 0.03.
Learn more about mean on;
brainly.com/question/1136789
#SPJ1
SEARCH UP:CNN 10 April 9th,2021
Watch the video then give me 10 facts
Answers
Answer:
Ketchup
Step-by-step explanation:
What is the size of angle a?

Answers
Answer:
60 degrees
Step-by-step explanation:
The total angles of a circle add up to 360 so to find a missing angle, subtract the figures already given from 60. The angles given total to (140+125+35) = 300. To find angle a, you subtract the 300 from 360. 360-300 = 60 degrees. Therefore, angle a is 60 degrees
Solve - x/3 > 5
A. x≤-15
B. x2 -15
C. x ≥ 15
D. x≤ 15
Answers
Answer:
d
Step-by-step explanation:
-x/3<5
-x< 5x3
-x<15
(there is an assumed 1 in front of the x)
-1x<15
x/-1<15* -1
x>-15
sign switches when we deal with negative values mutiplying and dividing
hope this helped<3
Below are the fees of a parking lot.
First 2 hours = $5
Every 1/2 hour (or part of a half hour) afterward = $3.50
Mr. Garcia parked his car from 5:00pm to 11:15pm on the same day. How much did he pay for par
Answers
Answer:
145.54$
Step-by-step explanation:
Hope this help! <3
Possible outcomes for a discrete uniform distribution are the integers 2 to 9 inclusive. What is the probability of an outcomeless than 5? A. 37.5%.
B. 50.0%. C. 62.5%
Answers
The probability of an outcome less than 5 in a discrete uniform distribution ranging from 2 to 9 inclusive is 37.5%.
In a discrete uniform distribution, each outcome has an equal probability of occurring. In this case, the range of possible outcomes is from 2 to 9 inclusive, which means there are a total of 8 possible outcomes (2, 3, 4, 5, 6, 7, 8, 9).
To calculate the probability of an outcome less than 5, we need to determine the number of outcomes that satisfy this condition. In this case, there are 4 outcomes (2, 3, 4) that are less than 5.
The probability is calculated by dividing the number of favorable outcomes (outcomes less than 5) by the total number of possible outcomes. So, the probability is 4/8, which simplifies to 1/2 or 0.5.
Therefore, the correct answer is B. 50.0%. The probability of an outcome less than 5 in this discrete uniform distribution is 50%, or equivalently, 0.5.
Learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
If a rectangle has an area of x^2+x-20 and a width of x-4, what is the length?
Answers
Answer:
This (x - 5) represents the length of the rectangle.
Step-by-step explanation:
The formula for the area of a rectangle of length L and width W is A = L * W.
Here, the width is x - 4 and the area is x^2 + x - 20. Dividing the width (x - 4) into the area results in an expression for the length:
x - 4 / x^2 + x - 20
Let's use synthetic division here. It's a little faster than long division.
If the divisor in long division is x - 4, we know immediately that the divisor in synthetic division is 4:
4 / 1 1 -20
4 20
--------------------
1 5 0
This synthetic division results in a remainder of 0. This tells us that 4 (or the corresponding (x - 4) is indeed a root of the polynomial x^2 + x - 20, and so *(x - 4) is a factor. From the coefficients 1 and 5 we can construct the other factor: (x - 5). This (x - 5) represents the length of the rectangle.
Select the correct answer.
What is the range of this function?
2r
TT
y
2-
-2-
-3-
TO
211
-X

Answers
The range of the function graphed in this problem is given as follows:
All real values.
How to obtain the domain and range of a function?The domain of a function is obtained as the set containing all the values assumed by the independent variable x of the function, which are also all the input values assumed by the function.The range of a function is obtained as the set containing all the values assumed by the dependent variable y of the function, which are also all the output values assumed by the function.From the graph of the function given in this problem, y assumes all real values, which represent the range of the function.
Learn more about domain and range at https://brainly.com/question/26098895
#SPJ1
Calculate the expected time for the following activities. Please
provide formulas and key for all variables.
Answers
The expected time for activities, use the formula for expected value and multiply the time for each activity by its probability. Therefore, the expected time for these activities is 2.8 hours.
To calculate the expected time for activities, we can use the formula for expected value.
The expected value is calculated by multiplying the time for each activity by its probability of occurrence, and then summing up these values. The formula for expected value is: Expected Value = (Time1 * Probability1) + (Time2 * Probability2) + ... + (TimeN * ProbabilityN) Here's a step-by-step example:
1. List all the activities and their corresponding times and probabilities.
2. Multiply the time for each activity by its probability.
3. Sum up the values obtained in step 2.
For example, let's say we have two activities: Activity 1: Time = 2 hours, Probability = 0.6 Activity 2: Time = 4 hours, Probability = 0.4 Using the formula, we calculate the expected time as follows: Expected Time = (2 hours * 0.6) + (4 hours * 0.4) = 1.2 hours + 1.6 hours = 2.8 hours
Therefore, the expected time for these activities is 2.8 hours.
Here full question is not provided but the full answer given above.
Remember, this is just one example, and you can use the same formula for any number of activities with their respective times and probabilities. In summary, to calculate the expected time for activities, use the formula for expected value and multiply the time for each activity by its probability. Then, sum up these values to get the expected time.
Learn more about multiply here:
https://brainly.com/question/30875464
#SPJ11
a postal worker counts the number of complaint letters received by the united states postal service in a given day. identify the type of data collected.
Answers
When a postal worker counts the number of complaint letters received by the united states postal service in a given day, the type of data collected is quantitative.
How to explain the dataQuantitative data is data that can be measured and expressed in numbers. In this case, the number of complaint letters received by the United States Postal Service in a given day can be measured and expressed as a number.
Qualitative data, on the other hand, is data that cannot be measured or expressed in numbers. For example, the contents of the complaint letters would be qualitative data.
Learn more about data on
https://brainly.com/question/26711803
#SPJ1
Which choice represents the expression below as a single exponential
expression?
7.16.7.17
A. 7.142
B. 7.113.7.113
C. 7.113
D. 711

Answers
Answer:
C) (7.1)^13
Step-by-step explanation:
When you multiply numbers with the same bases but different exponents, the base stays the same, but the exponents get added:
a^x*a^y=a^(x+y)
(7.1)^6*(7.1)^7=(7.1)^(6+7)=(7.1)^13
Therefore, the correct answer is C) (7.1)^13
Answer:
C
Step-by-step explanation:
When multiplying numbers with exponents, you always add the exponents.
7.1^6+7
7.1^13
Hence, C
Hope it helps!
The yearly depreciation rate for a car is modeled by r = 1 - (V/C)^1/n, where V'is the value of the car after n years, and C'is the original cost. (a) Determine the depreciation rate for a car that originally cost S20,000 and is worth $12,000 after 4 yr. Round to the nearest tenth of a percent. (b) Determine the original cost of a car that has a yearly depreciation rate of 11% and is worth $10,000 after 2 yr. Round to the nearest S100 Part 1 of 2 (a) The depreciation rate is approximately __ % per year. Round to the nearest tenth of a percent. Part 2 of 2 (b) The original cost of a car is approximately $ __ Round to the nearest S100.
Answers
(a) The depreciation rate for the car is approximately 16.6% per year. (b) The original cost of the car is approximately $18,200.
(a) The depreciation rate for the car is approximately 16.6% per year. (b) The original cost of the car is approximately $18,200.
To find the depreciation rate in part (a), we can use the formula r = 1 - (V/C)^1/n, where V = $12,000, C = $20,000, and n = 4. Plugging these values in, we get r = 1 - (12,000/20,000)^(1/4) ≈ 0.166, or 16.6% rounded to the nearest tenth of a percent.
To find the original cost of the car in part (b), we can use the formula V = C(1 - r)^n, where V = $10,000, r = 0.11, and n = 2. Solving for C, we get C = V / (1 - r)^n = 10,000 / (1 - 0.11)^2 ≈ 18,200, rounded to the nearest $100.
To know more about depreciation rate, refer here:
https://brainly.com/question/30531944#
#SPJ11
lol pls help me lol. I need to get this test done in like 10-20 minutes. I will give brainlyest.
Which number is not in scientific notation? (1 point)
A.) 7 • 1024
B.) 0.8 • 103
C.) 1.09 • 10–2
D.) 1.8 • 10–5
