Answers
216.66
169π-100π=69π
69*3.14= 216.66
Related Questions
Solve each equation.
1) 14=3m + 4
Answers
M=3 1/3

I neeeeed heeeelp please

Answers
Answer:
10b/y^2
Step-by-step explanation:
Hope this helps! :)
Im too tired for this man

Answers
PLEASE HELP ME ASAP ILL GIVE BRAINLIEST
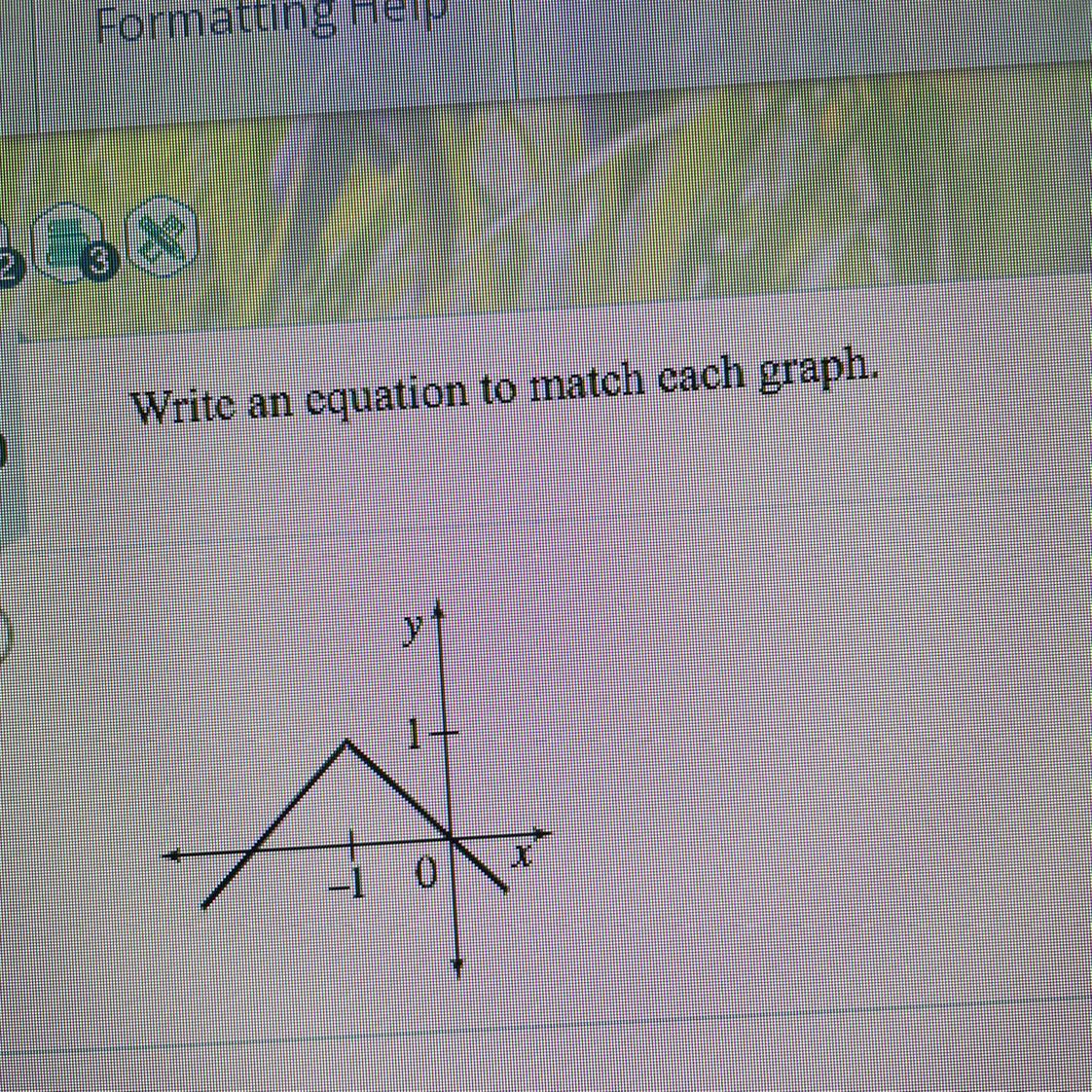
Answers
The absolute value function that matches the graph is given as follows:
y = -|x + 1| + 1.
How to define the absolute value function?An absolute value function of vertex (h,k) is defined as follows:
y = a|x - h| + k.
In which a is the leading coefficient.
The coordinates of the vertex in this problem are given as follows:
(-1, 1).
Hence:
y = a|x + 1| + 1.
The function is reflected over the x-axis with a slope of -1, hence the leading coefficient a is given as follows:
a = -1.
Thus the function is:
y = -|x + 1| + 1.
More can be learned about absolute value functions at brainly.com/question/3381225
#SPJ1
Can someone help me Solve:
-2√3+√75=
Answers
Answer:
\(3\sqrt{3}\)------------------
Simplify in below steps:
\(-2\sqrt{3} +\sqrt{75} =\)\(-2\sqrt{3} +\sqrt{25*3} =\)\(-2\sqrt{3} +\sqrt{5^2*3} =\)\(-2\sqrt{3} +5\sqrt{3} =\)\(3\sqrt{3}\)HELP ILL MARK BRAINIEST
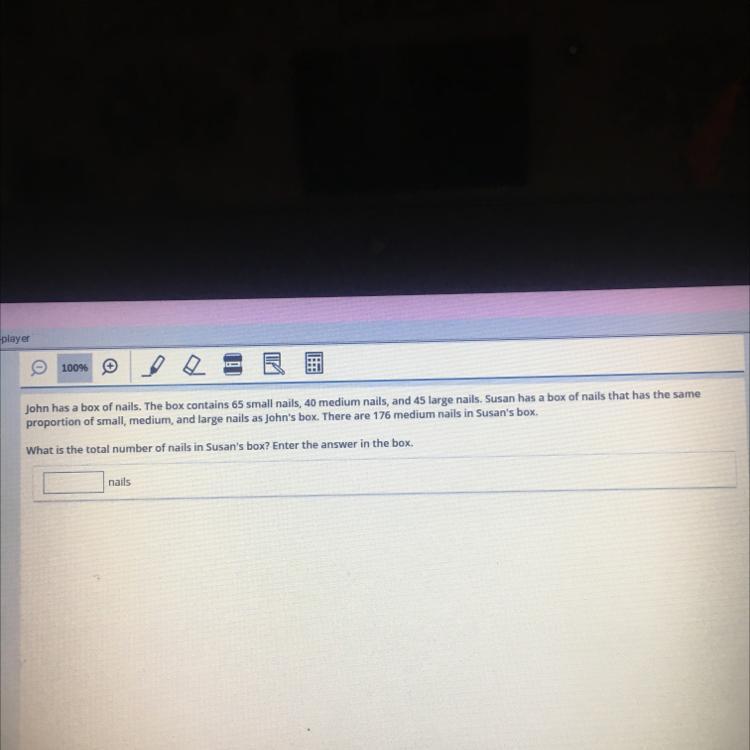
Answers
Answer:
medium nails in John = 40
medium nails in susan = 176
40/176
=5/22
so proportion is 5:22
Step-by-step explanation:
Hope this helps, have a great day!
Answer:
there no cartoon tho so I can really help but put one up
This year, the number of raffle tickets sold for a school's extracurricular activities fundraiser is 848. It is estimated that the number of raffle tickets sold will increase by 5% each year. Find the total number of raffle tickets sold at the end of 9 years.
Select the correct answer below:
9,158
9,351
9,818
10,666
Answers
This year, the number of raffle tickets sold for a school's extracurricular activities fundraiser is 848. It is estimated that the number of raffle tickets sold will increase by 5% each year.
The total number of raffle tickets sold at the end of 9 years is approximately 9,818.
To find the total number of raffle tickets sold at the end of 9 years, we need to calculate the number of tickets sold each year and sum them up.
Starting with the initial number of tickets sold, which is 848, we will increase this number by 5% each year for a total of 9 years.
Year 1: 848 + (5% of 848) = 848 + 42.4 = 890.4
Year 2: 890.4 + (5% of 890.4) = 890.4 + 44.52 = 934.92
Year 3: 934.92 + (5% of 934.92) = 934.92 + 46.746 = 981.666
Year 9: Ticket sales at the end of 9 years = Number of tickets sold in Year 8 + (5% of Year 8 sales)
Year 9: Total = 1,399.585 + 69.97925 = 1,469.56425 ≈ 1,469.56
The total number of raffle tickets sold at the end of 9 years is approximately 1,469.56.
The correct option is 9,818.
For more questions on raffle tickets
https://brainly.com/question/2083262
#SPJ8
Find the approximate area of the shaded region. Use 3.14 for pi

Answers
The area of the shaded region of the rectangle is approximately 573.92 square feet.
What is the area of the shaded region?The figure in the image is that of a rectangle with a semi-circle inscribed in it.
The area of rectangle is expressed as:
Area = Length × Width
The area of semi-circle is expressed as:
Area = 1/2 × πr²
To determine the area of the shaded region, we simply subtract the area of the semi-circle from the area of the rectangle.
Area of shaded region = area of rectangle - area of semi-circle
Area of shaded region = ( Length × Width ) - ( 1/2 × πr² )
From the image:
Length = 40 ft
Width = 20 ft
Radius r = 12 ft
Plug the values into the above formula:
Area of shaded region = ( Length × Width ) - ( 1/2 × πr² )
Area of shaded region = ( 40 × 20 ) - ( 1/2 × 3.14 × 12² )
Area of shaded region = ( 800 ) - ( 226.08 )
Area of shaded region = 573.92 ft²
Therefore, the area is approximately 573.92 square feet.
Learn more about area of rectangle here: brainly.com/question/12019874
#SPJ1
7(4p+2q+3r) apply the distributive property to create an equivalent expression
Answers
Answer:
28p + 14q + 21r
Step-by-step explanation:
7(4p + 2q + 3r) ← multiply each term in the parenthesis by the 7 outside
= 28p + 14q + 21r
Use the function f(x) to answer the questions:
f(x) = 2x2 − 5x + 3
Part A: What are the x-intercepts of the graph of f(x)? Show your work.
Part B: Is the vertex of the graph of f(x) going to be a maximum or a minimum? What are the coordinates of the vertex? Justify your answers and show your work.
Part C: What are the steps you would use to graph f(x)? Justify that you can use the answers obtained in Part A and Part B to draw the graph.
Answers
The x-intercepts of the graph of f(x) are x = 3/2 and x = 1,the Vertex of the graph of f(x) is (5/4, 3/8), and it is a minimum point, The vertex is at (5/4, 3/8). This is the minimum point of the graph.
Part A: To find the x-intercepts of the graph of f(x), we set f(x) equal to zero and solve for x.
2x^2 - 5x + 3 = 0
To factor this quadratic equation, we look for two numbers that multiply to give 3 (the coefficient of the constant term) and add up to -5 (the coefficient of the linear term). These numbers are -3 and -1.
2x^2 - 3x - 2x + 3 = 0
x(2x - 3) - 1(2x - 3) = 0
(2x - 3)(x - 1) = 0
Setting each factor equal to zero, we get:
2x - 3 = 0 --> x = 3/2
x - 1 = 0 --> x = 1
Therefore, the x-intercepts of the graph of f(x) are x = 3/2 and x = 1.
Part B: To determine whether the vertex of the graph of f(x) is a maximum or a minimum, we look at the coefficient of the x^2 term, which is positive (2 in this case). A positive coefficient indicates that the parabola opens upwards, so the vertex will be a minimum.
To find the coordinates of the vertex, we can use the formula x = -b/2a. In the equation f(x) = 2x^2 - 5x + 3, the coefficient of the x term is -5, and the coefficient of the x^2 term is 2.
x = -(-5) / (2*2) = 5/4
Substituting this value of x back into the equation, we can find the y-coordinate:
f(5/4) = 2(5/4)^2 - 5(5/4) + 3 = 25/8 - 25/4 + 3 = 3/8
Therefore, the vertex of the graph of f(x) is (5/4, 3/8), and it is a minimum point.
Part C: To graph f(x), we can use the information obtained in Part A and Part B.
- The x-intercepts are x = 3/2 and x = 1. These are the points where the graph intersects the x-axis.
- The vertex is at (5/4, 3/8). This is the minimum point of the graph.
We can plot these points on a coordinate plane and draw a smooth curve passing through the x-intercepts and the vertex. Since the coefficient of the x^2 term is positive, the parabola opens upwards, and the graph will be concave up.
Additionally, we can consider the symmetry of the graph. Since the coefficient of the linear term is -5, the line of symmetry is given by x = -(-5) / (2*2) = 5/4, which is the x-coordinate of the vertex. The graph will be symmetric with respect to this line.
By connecting the plotted points and sketching the curve smoothly, we can accurately graph the function f(x).
For more such questions on Vertex .
https://brainly.com/question/28747454
#SPJ8
A line is parallel to y = 3x - 2 and
intersects the point (3, 5).
How can we find the equation of
this parallel line?
We can use the slope formula: m = 12-₁
We can use the point-slope formula:
y-y₁ = m(x-x₁d
of Science. All Rights Reserved
Answers
Answer:
y = 3x - 4
Step-by-step explanation:
compare y = mx + c with y = 3x - 2, then
slope for the 1st line, m1 = 3
for parallel lines m1 = m2
m2 = 3
from y-y1 = m(x-x1)
(x1,y1) = (3,5)
y - 5 = 3(x - 3)
y - 5 = 3x - 9
collecting like terms
y = 3x -9 + 5
y = 3x - 4
Answer: The slope is 3
Step-by-step explanation: Parallel lines have the same slope, but different y-intercepts, so the slope of the line is also 3.
Can y’all please help me with this y=-16 + 29t+ 6
Answers
Answer: m=29
Step-by-step explanation:
What is the area of this figure? 11 mm 3 mm 2 mm 2 mm 4 mm 2 mm 5 mm 3 mm Write your answer using decimals. Use 3.14 for л.

Answers
Answer: 116.985 mm2
Step-by-step explanation:

Please help!!!
Question 7 of 10
Which of the following rational functions is graphed below?
A. F(x)= 4/ x-1
B. F(x)= x+4/ x-1
C. F(x)= x(x-1)/ (x+4)
D. F(x)= x/ (x+4)(x-1)

Answers
The rational function graphed in this problem is given as follows:
D. F(x) = x/[(x + 4)(x - 1)]
How to define the rational function?The vertical asymptotes are the values of x which are outside the domain, which in a fraction are the zeroes of the denominator, hence they are given as follows:
x= -4 and x = 1.
Hence the denominator of the function is given as follows:
(x + 4)(x - 1).
The intercept is given as follows:
x = 0.
Hence the numerator is:
x.
Thus the function is given as follows:
D. F(x) = x/[(x + 4)(x - 1)]
More can be learned about rational functions at https://brainly.com/question/1851758
#SPJ1
Leslie wants to invest $3,800.00 in a savings account that pays 4.8% simple interest.
How many years will it take for this investment to triple in value? Round your answer to the nearest tenth of a year.
It will take _______ years for this investment to triple in value.

Answers
Answer:
It will take 41.7 years for this investment to triple in value.
Step-by-step explanation:
Here is the formula for simple interest
\(A=P(1+rt)\)
Lets solve for \(t\).
Divide both sides by \(P\).
\(\frac{A}{P}=rt+1\)
Subtract 1 from both sides.
\(\frac{A}{P}-1=rt\)
Divide both sides by \(r\).
\(\frac{\frac{A}{P}-1}{r} =t\)
To write \(-1\) as a fraction with a common denominator, multiply by \(\frac{P}{P}\) .
\(\frac{\frac{A}{P}-1*\frac{P}{P}}{r} =t\)
\(\frac{\frac{A}{P}*\frac{-P}{P}}{r} =t\)
Combine the numerators over the common denominator.
\(\frac{\frac{A-P}{P} }{r} =t\)
Multiply the numerator by the reciprocal of the denominator.
\(t=\frac{A-P}{Pr}\)
We are given
\(P=3800\\r=0.048\)
We need to find what amount is triple his money.
\(3800*3=11400\)
\(A=11400\)
Substitute our numbers into the equation for \(t\).
\(t=\frac{11400-3800}{3800*0.048}\)
Factor 3800 out of 11400.
\(t=\frac{3800*3-3800}{3800*0.048}\)
Factor 3800 out of −3800.
\(t=\frac{3800*3-3800*-1}{3800*0.048}\)
Factor 3800 out of \(3800*3-3800*-1\).
\(t=\frac{3800*(3-1)}{3800*0.048}\)
Cancel the common factor of 3800.
\(t=\frac{3-1}{0.048}\)
Simplify.
\(t=\frac{2}{0.048}\)
\(t=41.666\)
Merry Christmas!
Solve:
(5 × 4) × (16 ÷ 8) × (24 − 22) =
Answers
Answer:
80
Step-by-step explanation:
used a calculator
Ciara throws four fair six-sided dice. The faces of each dice are labelled with the numbers 1, 2, 3, 4, 5, 6 Work out the probability that at least one of the dice lands on an even number.
Answers
The likelihood that one or more of the dice will land on an even number is 1296.
How does probability work?The likelihood of an event is quantified by its probability, which is a number. It is stated as a number between 0 and 1, or in percentage form, as a range between 0% and 100%. The likelihood of an event increasing with probability of occurrence.
According to the given information:Four 6-sided dice are rolled what is the probability that at least two dice show least 2 die the same.
For 2 of the same: 5×5×642) =900
For 3 of the same: 5×643) =120
For 4 of the same: 644) =6
Combined: 900+120+6=1026
Total possibilities: 64=1296
To know more about probability visit:
https://brainly.com/question/30034780
#SPJ1
The probability that at least one of the dice lands on an even number is 15/16 or approximately 0.938.
What is probability?
Probability is a measure of the likelihood of an event occurring. It is a number between 0 and 1, where 0 means the event is impossible and 1 means the event is certain to happen. The probability of an event can be calculated by dividing the number of favorable outcomes by the total number of possible outcomes.
We can solve this problem by finding the probability that all four dice land on odd numbers and then subtracting this probability from 1 to get the probability that at least one of the dice lands on an even number.
The probability that one dice lands on an odd number is 3/6 = 1/2, and the probability that all four dice land on odd numbers is:
(1/2) × (1/2) × (1/2) × (1/2) = 1/16
Therefore, the probability that at least one of the dice lands on an even number is:
1 - 1/16 = 15/16
So the probability that at least one of the dice lands on an even number is 15/16 or approximately 0.938.
To learn more about probability from the given link:
https://brainly.com/question/30034780
#SPJ1
ES = ___ units
Round your answer to the nearest tenth.

Answers
ES = 10.63 units
How to find the length of the line ?The length of the line segment connecting any two points represents the distance between them. There is just one line that connects the two places. Therefore, by measuring the length of the line segment that connects the two sites, the distance between them may be determined.
When given a straight line on a graph, you can find the length of this line by using the Distance Between Two Points Formula. This formula uses the vertices of the beginning and ending points of a straight line to find the length of the line, which is the distance between the two points.
The Distance Between Two Points Formula is:
= √(( x₂ – x₁ )² + ( y₂ – y₁) ²)
The vertices of the line ES are E ( -3, -4 ) and S ( 4, 4 ).
The distance is:
= √(( 4 – (-3) )² + ( 4 ( - 4 )) ²)
= 10. 63 units
Find out more on distance at https://brainly.com/question/23848540
#SPJ1
The diagonals of parallelogram ABCD intersect at P. Which statements must be true? Select all that apply.

Answers
The statements that will be true about parallelogram ABCD are: A, B, D, and E.
Properties of a Parallelogram -
Diagonals of a parallelogram bisect each other into congruent segments.
Opposite angles and sides of a parallelogram are always congruent.
Alternate interior angles are always congruent in measure.
Thus, the following would be true of parallelogram ABCD:
AP ≅ CP (congruent segment's of a bisected diagonal)
BC ≅ AD (congruent opposite sides)
∠CAD ≅ ∠ACB (congruent angles)
∠BPC ≅ ∠APD (congruent angles)
Therefore, the statements that will be true about parallelogram ABCD are: A, B, D, and E.
Learn more about parallelogram on:
brainly.com/question/3050890
#SPJ1
Convert f ( x ) = 48 ( 1.02 ) x to the form f ( x ) = a e k x . Round k to 4 decimal places.
Answers
The exponential function can be rewritten as:
f(x) = 48*e^(0.0198*x)
How to transform the function?Here we start with the exponential function:
f(x) = 48*(1.02)^x
And we want to write this in the general form:
f(x) =a*e^(kx)
Notice that we can write the second form as:
f(x) = a*[e^k]^x
So, comparing this with the given exponential, we will get:
a = 48
e^k = 1.02
Apply the natural logarithm in both sides:
ln(e^k) = ln(1.02)
k*ln(e) = ln(1.02)
k = ln(1.02) = 0.0198
Then the exponential function is:
f(x) = 48*e^(0.0198*x)
Learn more about exponential functions at:
https://brainly.com/question/2456547
#SPJ1
if the total profit per month of a company is Rs 200,000 and its revenue per month can be obtained by adding Rs. 20,000 to the twice the cost per month, find the revenue and cost per month. ..?
Answers
Answer:
okey baik dan sangat bagus
ANSWER. Write the word or phrase that best completes each statement or answers the question. Solve the problem. 1) Two kinds of crated cargo, A and B, are to be shipped by truck. Each crate of cargo A is 50 cubic feet in volume and weighs 200 pounds, whereas each crate of cargo B is 10 cubic feet volume and weighs 360 pounds. The shipping company charges $75 per crate for cargo A and $100 per crate for cargo B. The
Answers
Answer:
To complete the problem statement it is needed:
1.- the volume and weight capacity of the truck, because these will become the constraints.
2.- In order to formulate the objective function we need to have an expression like this:
" How many of each type of crated cargo should the company shipped to maximize profit".
Solution:
z(max) = 175 $
x = 1
y = 1
Assuming a weight constraint 700 pounds and
volume constraint 150 ft³ we can formulate an integer linear programming problem ( I don´t know if with that constraints such formulation will be feasible, but that is another thing)
Step-by-step explanation:
crated cargo A (x) volume 50 ft³ weigh 200 pounds
crated cargo B (y) volume 10 ft³ weigh 360 pounds
Constraints: Volume 150 ft³
50*x + 10*y ≤ 150
Weight contraint: 700 pounds
200*x + 360*y ≤ 700
general constraints
x ≥ 0 y ≥ 0 both integers
Final formulation:
Objective function:
z = 75*x + 100*y to maximize
Subject to:
50*x + 10*y ≤ 150
200*x + 360*y ≤ 700
x ≥ 0 y ≥ 0 integers
After 4 iterations with the on-line solver the solution
z(max) = 175 $
x = 1
y = 1
The circumference would ……. For example, a circle with a radius of 3 feet would have a circumference that is about 18 feet. When the radius doubles to 6 feet, the circumference is about ………. feet.
Answers
Answer:
37.7 feet
Step-by-step explanation:
The circumference of a circle can be calculated using the formula: Circumference = 2 * π * radius, where π (pi) is approximately 3.14159.
For example, if we have a circle with a radius of 3 feet, its circumference would be approximately 18.85 feet (rounded to five decimal places).
When we double the radius to 6 feet, the circumference also doubles. In this case, the circumference would be approximately 37.70 feet (rounded to five decimal places).
In summary, when the radius of a circle doubles, the circumference also doubles, maintaining a direct proportional relationship between the two measurements.
26,720 inches are equal to _______ miles.
Answers
Answer: 0.42171717 miles
Step-by-step explanation:
for inches to mile conversion divide by 63350
so got 0.421717
explain how 4 2/6 is equivalant to 3 8/7
Answers
Question
The sum of four times a number and two is 14. Find the number.
Answers
Answer:3
Step-by-step explanation:let the number be x
4x+2=14
4x=14-2
4x=12
divide both sides by 4
4x/4=12/4
x=3
A county sales tax is 6%. Write the percent as a
fraction in simplest form.
o
Answers
Answer:
0.06
Step-by-step explanation:
0.06 is = to 6% because the percentage is out of 100 and 0.06 is out of a 100.
subtract 2 3/4 - 5/16
Answers
Answer:
2 7/16
Step-by-step explanation:
2 3/4 - 5/16 → 11/4 - 5/16 (convert 2 3/4 into an improper or top-heavy fraction)
11/4 - 5/16 → 44/16 - 5/16 (multiply 11/4 by 4/4 to make a common denominator)
44/16 - 5/16 = 39/16 (Subtract 44 - 5 = 39)
Simplify (convert back into mixed number)
39/16 = 2 7/16
Hope this helps!
an ice cream factory makes 210 quarts of ice cream in 2 hours. How many quarts could be made in 48 hours? what was that rate per day?
Answers
Camila has 6 bags of candy. She can pour 1/3 of a bag of candy into a bowl. How many bowls of candy can Camila make in all?
Answers
Answer:
18 Bowls of Candy
Step-by-step explanation:
Camila has 6 bags of candy, and she can pour 1/3 of a bag into a bowl. To determine how many bowls of candy she can make in total, we need to divide the total amount of candy by the amount of candy per bowl.
Since Camila can pour 1/3 of a bag into a bowl, it means she can make 3 bowls of candy with a full bag.
Now, we can calculate the total number of bowls of candy:
Total bowls of candy = (Number of bags) x (Bowls per bag)
Total bowls of candy = 6 bags x 3 bowls per bag
Total bowls of candy = 18 bowls
Therefore, Camila can make a total of 18 bowls of candy with her 6 bags of candy.
