HELP ME PLEASE OMG! WHY WON'T ANYONE HELP ME
Identify which of the following has the smaller slope. What is the difference of the slopes?

Answers
Answer:
put the points on the paper and then figure out how far apart they are
Related Questions
What is the product?

Answers
Answer:
third answer is correct
Step-by-step explanation:
hello,
we need to compute
5*(-1)+(-2)*(-1)=-5+2=-3
-6*(-1)+(2)*(-1)=6-2=4
so the correct answer is
-3
4
hope this helps
the sitting height of drivers must be considered in the design of a new car. the sitting height is measured from the seat to the top of the driver's head, and adults have sitting heights that are normally distributed with a mean of 35.4 in. and a standard deviation of 1.6 in. engineers are planning a design in which only the tallest 2% of adults will be unable to fit. find this sitting height. round your answer to 2 decimal places.
Answers
If the engineers are planning a car design in which only 25 of adults fit , then this sitting height is 38.68 inches .
To find the sitting height for the tallest 2% of adults, we first find z-score for upper 2% of standard Normal Distribution ;
we know ; that z = (x - μ)/σ ;
where z is = z core, x is = sitting height , μ is = mean sitting height, and
σ is = standard deviation of sitting heights.
From the normal table : Upper 2% of standard normal distribution have a z-score of approximately 2.05 ;
So , 2.05 = (x - 35.4)/1.6 ;
Multiplying both sides by 1.6, we get ;
⇒ 3.28 = x - 35.4
On adding 35.4 to both sides, we get:
⇒ x = 38.68 ;
Therefore, the sitting height for the tallest 2% of adults is 38.68 inches .
Learn more about Normal Distribution here
https://brainly.com/question/24056655
#SPJ4
Calculate the slope of the line which passes through the points (8,7) and (11, 3)
Answers
Answer:
negative 1 1/3
Step-by-step explanation:
you do y2 minus y1 over x2 minus x1 then you simplify.
4x+8<2x+2
this has quite a bit of points
Answers
Answer:
x= −3Step-by-step explanation:
4x+8<2x+2
Subtract 2x from both sides.
4x+8−2x<2
Combine 4x and −2x to get 2x.
2x+8<2
Subtract 8 from both sides.
2x<2−8
Subtract 8 from 2 to get −6.
2x<−6
Divide both sides by 2. Since 2 is positive, the inequality direction remains the same.
x<
2
−6
Divide −6 by 2 to get −3.
x<−3
Hope this helps :)
Pls make brainliest :3
And have an amazing day <3
Answer: x < -3
Step-by-step explanation:
I go out star gazing again, but this time the chances of seeing a shooting star are 80% in any given hour. Assuming that the probability of seeing a shooting star is uniform for the entire hour, what is the probability that I will see one during the first 15 minutes of the hour I am out
Answers
The probability of seeing a shooting star during the first 15 minutes of the hour is approximately 19.95%
To solve this problem, we need to use conditional probability. We want to find the probability of seeing a shooting star during the first 15 minutes of the hour given that the chances of seeing a shooting star in any given hour are 80%.
First, we need to determine the probability of seeing a shooting star in the first 15 minutes of the hour. Since the probability is uniform for the entire hour, we can assume that the probability of seeing a shooting star in any given minute is 80% divided by 60 (the number of minutes in an hour), which is approximately 1.33%.
To find the probability of seeing a shooting star during the first 15 minutes of the hour, we need to add up the probabilities of seeing a shooting star in each of the 15 minutes. This can be calculated as follows:
P(seeing a shooting star in the first 15 minutes) = P(seeing a shooting star in minute 1) + P(seeing a shooting star in minute 2) + ... + P(seeing a shooting star in minute 15)
= 15 x 1.33%
= 19.95%
Therefore, the probability of seeing a shooting star during the first 15 minutes of the hour is approximately 19.95%. This means that if you go out star gazing again and the chances of seeing a shooting star are 80%, there is a 19.95% chance that you will see one during the first 15 minutes of the hour you are out.
Know more about shooting star here:
https://brainly.com/question/31451954
#SPJ11
`
Profit, P(x), is the difference between revenue, R(x), and cost, C(x), so P(x) = R(x) - C(x).
Which expression represents P(x), if R(x) = 2x²-3x³ + 2x - 1 and C(x)=x²-x²+2x+3?
2283x³ + x² - 4
3r3r³r² + 4x + 2
2¹-32³-2² + 4z +2
2-32³ +2²-4

Answers
The expression for P(x) is -3x³ - 4.
To find the expression for P(x), we need to subtract C(x) from R(x).
Given that R(x) = 2x² - 3x³ + 2x - 1 and C(x) = x² - x² + 2x + 3, we can substitute these values into the equation P(x) = R(x) - C(x):
P(x) = (2x² - 3x³ + 2x - 1) - (x² - x² + 2x + 3)
Simplifying, we can combine like terms:
P(x) = 2x² - 3x³ + 2x - 1 - x² + x² - 2x - 3
The x² terms cancel each other out, and the 2x and -2x terms also cancel each other out:
P(x) = -3x³ - 1 - 3
Simplifying further:
P(x) = -3x³ - 4
Therefore, the expression for P(x) is -3x³ - 4.
for such more question on expression
https://brainly.com/question/4344214
#SPJ8
we say a definite integral is improper if one is infinite, or if the is infinite.
One _____is infinite, or if
The_______is infinite
Answers
From the given data, we say a definite integral is improper if one endpoint is infinite, or if the integrand is infinite.
One endpoint is infinite, or if the integrand is infinite, the definite integral cannot be evaluated using the usual techniques. Instead, we must use the concept of a limit to find the value of the integral, if it exists. In the case where one endpoint is infinite, we take a limit as a variable approaches infinity. In the case where the integrand is infinite, we may need to split the integral into pieces or use some other method to deal with the singularity.
Learn more about definite integral here: brainly.com/question/27746495
#SPJ4
Suppose that a chemist is mixing two acid solutions, one of 50% concentration and the other of 60% concentration. Which of the following concentrations could not be obtained? 52%,54%,58%,64%
Answers
A mixture with 64% concentration cannot be obtained
Estimation of averagesIn mathematics and statistics, average refers to the sum of a group of values divided by n, where n is the number of values in the group. An average is also known as a mean.
The average is a measure of central tendency, meaning it reflects a typical value in a given set. Averages are used quite regularly to determine final concentration of two or mixtures.
Since the mixture consists of a 50% and a 60% concentration of acid solutions. The average concentration of the final mixture is within 50% and 60% and can be represented by the inequality
50 < x < 60
It cannot not be 50% or lesser in concentration and it cannot be 60% or more in concentration.
From the given options 52%, 54% and 58% are all within this range. Only 64% is outside this range.
Therefore, 64% concentration cannot be obtained.
Learn more on averages here:
https://brainly.com/question/20118982
#SPJ4
a surveyor is standing 50 feet from the base of a large tree and measures the angle of elevation to the top of the tree to be . how tall is the tree to the nearest foot?
Answers
71.5° should be the angle of elevation to the summit of the tree. The tree to the nearest foot is 149.4ft.
Between the horizontal line and the line of sight, an angle called the angle of elevation is created. An angle of elevation is produced when the line of sight is upward from the horizontal line. When it lies between the line of sight and the horizontal line, the angle of elevation is generated. The angle created, known as the angle of elevation, occurs when the line of sight is above the horizontal line. However, the line of sight is downward toward the horizontal line in the depression angle. The angle of elevation is the angle formed by the horizontal line of sight and the object when a person stands and looks up at something.
tan 71.5°=opp/hyp
tan 71.5°=y/50
y=50(tan 71.5°)
y=50(tan 71.5°)
y=50(2.98868)
y=149.4ft
Learn more about angle of elevation here
https://brainly.com/question/88158
#SPJ4
The logistic growth model P(1) -1550represents the population of a bacterium in a culture tube1 + 43.29e-0.334after t hours. What was the initial amount of bacteria in the population?A) 36B) 40C) 34D) 35
Answers
Given the logistic growth model
\(P(t)=\frac{1550}{1+43.29e^{-0.334t}}\)we want to find the initial amount of bacteria in this problem. If we are talking about the initial amount, we have t = 0 since time doesn't lapse yet for the growth of the bacteria. Hence, for t = 0, the amount of bacteria will be
\(\begin{gathered} P(0)=\frac{1550}{1+43.29e^{-0.334(0)}} \\ P(0)=\frac{1550}{1+43.29(1)}=34.9966\approx35 \end{gathered}\)Find x
8(x-27)+49=87+28x
Answers
Answer:
x = -12.7
Step-by-step explanation:
\(8(x-27)+49=87+28x\\\\8x-167=87+28x\\\\8x-167+167=87+28x+167\\\\8x=28x+254\\\\8x-28x=28x-28x+254\\\\-20x=254\\\\\frac{-20x=254}{-20}\\\\ \boxed{x=-12.7}\)
Hope this helps.
Answer:
x=-127/10 or x= -12.7
Step-by-step explanation:
8(x−27)+49=87+28x
Step 1: Simplify both sides of the equation.
8(x−27)+49=87+28x
(8)(x)+(8)(−27)+49=87+28x(Distribute)
8x+−216+49=87+28x
(8x)+(−216+49)=28x+87(Combine Like Terms)
8x+−167=28x+87
8x−167=28x+87
Step 2: Subtract 28x from both sides.
8x−167−28x=28x+87−28x
−20x−167=87
Step 3: Add 167 to both sides.
−20x−167+167=87+167
−20x=254
Step 4: Divide both sides by -20.
−20x/−20
=
254/−20
x=
−127/10
If you want to maximize your probability of winning, what threshold should you set for your strategy in a gameof 10 flips
Answers
It's important to approach any strategy with caution and understand its limitations.
If one wants to maximize their probability of winning in a game of 10 flips, they should set the threshold at 6.
This is because when playing a game of 10 coin flips, there are 2^10 or 1024 possible outcomes, with 512 of them resulting in a win, a loss, or a tie.
Therefore, setting the threshold at 6 ensures that they win at least 6 out of the 10 coin flips, resulting in a higher probability of winning.
However, it's worth noting that this strategy is not foolproof as it does not take into account the sequence of the coin flips.
For example, if the first 5 coin flips are tails and the last 5 are heads, setting the threshold at 6 would result in a loss.
Therefore, it's important to approach any strategy with caution and understand its limitations.
learn more about probability here:
https://brainly.com/question/31828911
#SPJ11
A table of values of a function f with continuous gradient is given. Findstudent submitted image, transcription available belowC ∇f · dr, where C has the parametric equations below. x = t4 + 1, y = t5 + t ,0 ≤ t ≤ 1
x/y 0 1 2
0 1 7 3
1 3 5 9
2 6 1 6
Answers
The value of the line integral ∫C ∇f · dr along the curve C is 13/6.
Here, we have to evaluate the line integral ∫C ∇f · dr, where C has the parametric equations \(x = t^4 + 1, y = t^5 + t\), and 0 ≤ t ≤ 1,
we need to find the gradient of the function f and then compute the dot product with the differential vector dr.
First, let's find the gradient of the function f from the table of values:
x/y 0 1 2
0 1 7 3
1 3 5 9
2 6 1 6
We have the values of f at different points (x, y) in the table:
f(0, 0) = 1
f(1, 0) = 3
f(2, 0) = 6
f(0, 1) = 7
f(1, 1) = 5
f(2, 1) = 1
f(0, 2) = 3
f(1, 2) = 9
f(2, 2) = 6
Now, let's find the gradient of f with respect to x and y:
∇f = (∂f/∂x) i + (∂f/∂y) j
To find the partial derivatives, we can use finite difference approximations:
∂f/∂x ≈ (f(x+1, y) - f(x-1, y)) / 2
∂f/∂y ≈ (f(x, y+1) - f(x, y-1)) / 2
Now, we can calculate the gradient at each point:
∇f(0, 0) = (∂f/∂x)_0 i + (∂f/∂y)_0 j
≈ (f(1, 0) - f(-1, 0)) / 2 i + (f(0, 1) - f(0, -1)) / 2 j
≈ (3 - 1) / 2 i + (7 - 1) / 2 j
≈ 1 i + 3 j
∇f(1, 0) = (∂f/∂x)_1 i + (∂f/∂y)_0 j
≈ (f(2, 0) - f(0, 0)) / 2 i + (f(1, 1) - f(1, -1)) / 2 j
≈ (6 - 1) / 2 i + (5 - 0) / 2 j
≈ 2.5 i + 2.5 j
∇f(2, 0) = (∂f/∂x)_2 i + (∂f/∂y)_0 j
≈ (f(3, 0) - f(1, 0)) / 2 i + (f(2, 1) - f(2, -1)) / 2 j
≈ (3 - 6) / 2 i + (1 - 0) / 2 j
≈ -1.5 i + 0.5 j
∇f(0, 1) = (∂f/∂x)_0 i + (∂f/∂y)_1 j
≈ (f(1, 1) - f(-1, 1)) / 2 i + (f(0, 2) - f(0, 0)) / 2 j
≈ (5 - 7) / 2 i + (3 - 1) / 2 j
≈ -1 i + 1 j
∇f(1, 1) = (∂f/∂x)_1 i + (∂f/∂y)_1 j
≈ (f(2, 1) - f(0, 1)) / 2 i + (f(1, 2) - f(1, 0)) / 2 j
≈ (1 - 5) / 2 i + (9 - 3) / 2 j
≈ -2 i + 3 j
∇f(2, 1) = (∂f/∂x)_2 i + (∂f/∂y)_1 j
≈ (f(3, 1) - f(1, 1)) / 2 i + (f(2, 2) - f(2, 0)) / 2 j
≈ (6 - 1) / 2 i + (6 - 5) / 2 j
≈ 2.5 i + 0.5 j
∇f(0, 2) = (∂f/∂x)_0 i + (∂f/∂y)_2 j
≈ (f(1, 2) - f(-1, 2)) / 2 i + (f(0, 3) - f(0, 1)) / 2 j
≈ (1 - 6) / 2 i + (0 - 3) / 2 j
≈ -2.5 i - 1.5 j
∇f(1, 2) = (∂f/∂x)_1 i + (∂f/∂y)_2 j
≈ (f(2, 2) - f(0, 2)) / 2 i + (f(1, 3) - f(1, 1)) / 2 j
≈ (6 - 1) / 2 i + (9 - 5) / 2 j
≈ 2.5 i + 2 j
∇f(2, 2) = (∂f/∂x)_2 i + (∂f/∂y)_2 j
≈ (f(3, 2) - f(1, 2)) / 2 i + (f(2, 3) - f(2, 1)) / 2 j
≈ (6 - 1) / 2 i + (6 - 5) / 2 j
≈ 2.5 i + 0.5 j
Now that we have the gradient ∇f at each point (x, y), we can compute the line integral along the curve C:
∫C ∇f · dr = ∫(0 to 1) ∇f · dr
The differential vector dr in cylindrical coordinates is given by:
dr = dx i + dy j
= (dx/dt) dt i + (dy/dt) dt j
= \((4t^3 dt) i + (5t^4 + dt) j\)
Now, compute the dot product ∇f · dr and integrate along the curve C:
∫C ∇f · dr = ∫(0 to 1) ∇f · dr
= ∫(0 to 1) (∇f · \((4t^3 dt) i\) + ∇f · \((5t^4 + dt) j\))
= ∫(0 to 1) (\(4t^3\) ∇f · i + (\(5t^4 + 1\)) ∇f · j) dt
Now, substitute the values of ∇f at each point (x, y):
∫C ∇f · dr = ∫(0 to 1) (\(4t^3\) (1) + (\(5t^4 + 1\)) (t)) dt
= ∫(0 to 1) \((4t^3 + 5t^5 + t)\) dt
Now, integrate with respect to t from 0 to 1:
∫C ∇f · dr = [\(t^4 + (5/6)t^6 + (1/2)t^2\)] |_(0 to 1)
∫C ∇f · dr = (1 + 5/6 + 1/2) - (0 + 0 + 0)
∫C ∇f · dr = (13/6)
Therefore, the value of the line integral ∫C ∇f · dr along the curve C is 13/6.
To know more about integral:
brainly.com/question/30714582
#SPJ12
6 = x(1 + 2x)
Ifx is a solution to the equation above and x > 0
what is the value olx
Answers
Answer:
1.5
Step-by-step explanation:
cause I said so and I'm big brained and you should listen to me because I should be doing 8th grade math but instead I'm doing 7th
hat is the maximum speed of a point on the outside of the wheel, 15 cm from the axle?
Answers
It depends on the rotational speed of the wheel. To calculate this speed, we need to know the angular velocity of the wheel.
The maximum speed of a point on the outside of the wheel, 15 cm from the axle, if we assume that the wheel is rotating at a constant rate, we can use the formula v = rω, where v is the speed of the point on the outside of the wheel, r is the radius of the wheel (15 cm in this case), and ω is the angular velocity of the wheel. Therefore, the maximum speed of a point on the outside of the wheel would be directly proportional to the angular velocity of the wheel.
The formula to calculate the maximum linear speed (v) is:
v = ω × r
where v is the linear speed, ω is the angular velocity in radians per second, and r is the distance from the axle (15 cm, or 0.15 meters in this case).
Once you have the angular velocity (ω) of the wheel, you can plug it into the formula and find the maximum speed of a point on the outside of the wheel.
Learn more about rotational speed here: brainly.com/question/17025846
#SPJ11
A box contains 7 plain pencils and 1 pen. A second box contains 3 color pencils and 3 crayons. One item from
each box is chosen at random. What is the probability that a pen from the first box and a crayon from the
second box are selected?
Write your answer as a fraction in simplest form.
Answers
The probability of selecting a pen from the first box is 1/8 (since there is only 1 pen out of 8 items in the box). The probability of selecting a crayon from the second box is 3/6 (since there are 3 crayons out of 6 items in the box).
To find the probability of both events happening together, we multiply the probabilities:
P(pen and crayon) = P(pen) x P(crayon)
P(pen and crayon) = (1/8) x (3/6)
Simplifying the fraction 3/6 to 1/2:
P(pen and crayon) = (1/8) x (1/2)
Multiplying the numerators and denominators:
P(pen and crayon) = 1/16
Therefore, the probability of selecting a pen from the first box and a crayon from the second box is 1/16.
Motorcycle travel 90 mph accelerates to pass a truck five seconds later the car is going 120 mph calculate the acceleration
Answers
Answer:
Explanation:
Let Vc be the velocity of the car and I'm the velocity of the motorcycle. If we convert their given values, we get:
Vc = 87 km/h * 1000m / 1km * 1h / 3600s = 24.17m/s
Vm = 95 km/h * 1000m / 1km * 1h / 3600s = 26.38m/s
Since their positions are equal after 17s we can stablish that:
Where d is the initial separation distance of 54m. Solving for a, we get:
Repacing the values:
What is the absolute value of -5
Answers
Answer:
5
Step-by-step explanation:
Help my math homework
Answers
Answer:
the question dear sister
Consider a cost-benefit-trade-off problem having the following data. Benefit Contribu tion per Unit of Each Activity Accept able Level Benefit 2 60 30 126 Unit cost$60 $50 a. Formulate a linear programming model for this problem on a spreadsheet. b. Use the spreadsheet to check the following solutions: (x1,32)(7,7. (7. 8), (8. 7), (8, 8) (8, 9), (9, 8). Which of these solutions are feasible? Which of these feasible solutions has the best value of the objective function? c. Express the model in algebraic fom. d. Use the graphical method to solve this model.
Answers
The value of the objective function at this point is Z = 840. The solution (7, 7) is feasible.
a. Formulation of linear programming model:To solve this problem, the following linear programming model can be used:x1 = Activity 1 (in units)x2 = Activity 2 (in units)Maximize Z = 60x1 + 50x2 subject to30x1 + 126x2 ≤ 4,752 (Acceptable limit)60x1 + 126x2 ≤ 8,436 (Benefit 1)Step-by-step explanation is given below:Function: Linear Programming modelSolution:
a. Formulation of linear programming model:To solve this problem, the following linear programming model can be used:x1 = Activity 1 (in units)x2 = Activity 2 (in units)Maximize Z = 60x1 + 50x2 subject to30x1 + 126x2 ≤ 4,752 (Acceptable limit)60x1 + 126x2 ≤ 8,436 (Benefit 1)
b. Checking for feasible solutionsWe need to check the following solutions:(x1, 32) (7, 7) (7, 8) (8, 7) (8, 8) (8, 9) (9, 8)Let us substitute the values in the linear programming model for each solution:Solution: (x1, 32)30x1 + 126(32) = 4,752 + 4,032 = 8,784 > 4,752 (Infeasible)Solution: (7, 7)30(7) + 126(7) = 966 < 4,752 (Feasible)60(7) + 126(7) = 1,092 < 8,436 (Feasible)Solution: (7, 8)30(7) + 126(8) = 5,070 > 4,752 (Infeasible)Solution: (8, 7)30(8) + 126(7) = 5,016 > 4,752 (Infeasible)Solution: (8, 8)30(8) + 126(8) = 5,196 > 4,752 (Infeasible)Solution: (8, 9)30(8) + 126(9) = 5,322 > 4,752 (Infeasible)Solution: (9, 8)30(9) + 126(8) = 5,358 > 4,752 (Infeasible)Therefore, only the solution (7, 7) is feasible.
c. Expressing the model in algebraic form:We have,x1 = Activity 1 (in units)x2 = Activity 2 (in units)Maximize Z = 60x1 + 50x2 subject to30x1 + 126x2 ≤ 4,752 (Acceptable limit)60x1 + 126x2 ≤ 8,436 (Benefit 1)The solution x = (7, 7) is feasible and optimal, with Z = 60(7) + 50(7) = 840.d. Using the graphical method:Below is the graph plotted for the above linear programming model:graph{(y-4752)/126<=-(3/2)x+316}The feasible region is given by the shaded region in the graph. The optimal solution is (7, 7), which is at the point of intersection of the two lines. The value of the objective function at this point is Z = 840.
Learn more about function :
https://brainly.com/question/29633660
#SPJ11
Paul is making a ball-toss game for his club booth at the fair. He wants to make the circumference of the holes at least 3 inches greater but not more than 4 inches greater than the circumference of the ball. One person suggests that Paul can make the diameter of the hole 1 inch greater than that of the ball. Another suggests the diameter should be 2inches greater. Which suggestion should Paul choose? Explain
Answers
Answer:
Paul can make the diameter of the hole 1 inch greater than that of the ballStep-by-step explanation:
we are going to assume a diameter of the hole has 6in
the radius of the ball is 3in
we looking at a range of the hole greater by (3<4)
we know that the circumference of a circle is given as
the circumference of the ball is
C=2πr
C=2*3.142*3
C=18.85in
The circumference of the hole is ( 1 inch greater )
C=2πr
say the diameter is 6in plus 1in = 7in
the radius =3.5in
C=2*3.142*3.5
C=21.99
compare with the ball the difference is 21.99-18.85
=3.14 which is in the range
The circumference of the hole is ( 2inches greater. )
C=2πr
say the diameter is 6in plus 2in = 8in
the radius =4in
C=2*3.142*4
C=25.13in
compare with the ball the difference is 25.13-18.85
=6.28 which is out of the range
If m∠2=6x+8 and m∠6=8x-6, find the value of x so that l||m.

Answers
Answer:
x = 7
Step-by-step explanation:
∠2 and ∠6 are known as alternate interior angles. These angles equal one another. Set up the following equation and solve for x.
\(m\angle2=m\angle6\\\\6x+8=8x-6\\\\8=2x-6\\\\14=2x\\\\7=x\)
100 POINTS!!! Please tell me how to do this I dont understand...

Answers
Answer:
\( \displaystyle x = 15\)
Step-by-step explanation:
by triangle midsegment theorem we obtain:
\( \displaystyle \frac{10x + 44}{2} = 8x - 23\)
simplify division:
\( \displaystyle 5x + 22 = 8x - 23\)
move 5x to right hand side and -23 to the left hand side and change its sign:
\( \displaystyle 22 + 23= 8x - 5x\)
simplify addition:
\( \displaystyle 8x - 5x = 45\)
collect like terms:
\( \displaystyle 3x = 45\)
divide both sides by 3:
\( \displaystyle x = 15\)
and we are done!
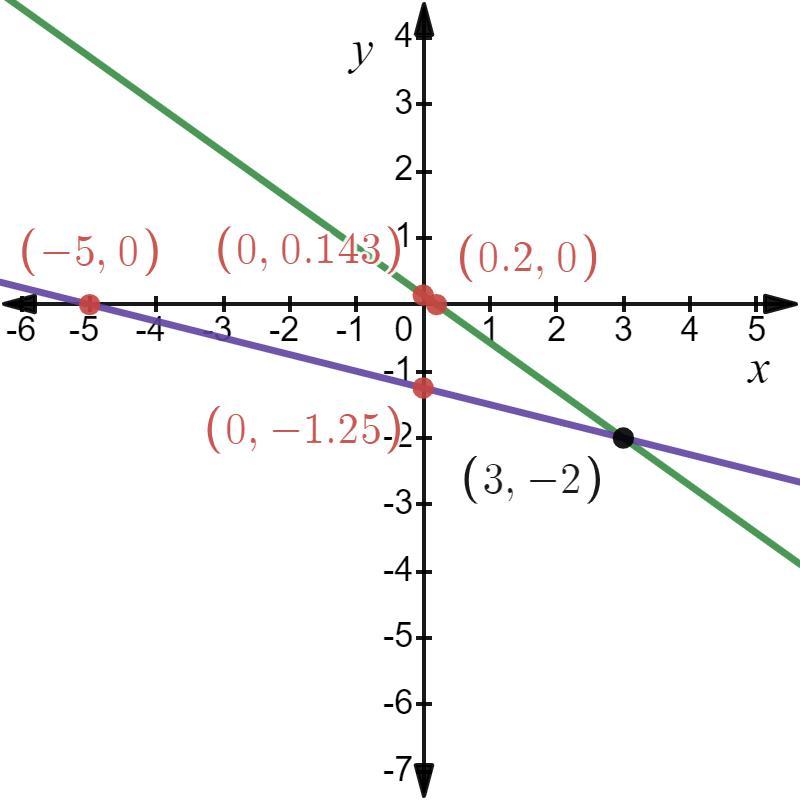
Solve graphically.
5x+7y=1 and x+4y=-5
Answers
Answer:
{x,y} = {3,-2}
Step-by-step explanation:
Then the intersection point is (3, -2). Then the solution of the equations will be (3, -2).
What is a linear equation?A connection between a number of variables results in a linear model when a graph is displayed. The variable will have a degree of one.
The linear equation is given as,
x/a + y/b = 1
Where 'a' is the x-intercept of the line and ‘b’ is the y-intercept of the line.
The equations are given below.
5x + 7y = 1
x + 4y = -5
Convert the equation into an intercept form. Then we have
From equation 1, then we have
5x + 7y = 1
x / (1/5) + y / (1/7) = 1
From equation 2, then we have
x + 4y = -5
x / (-5) + y / (-5/4) = 1
The lines are drawn below.
Then the intersection point is (3, -2). Then the solution of the equations will be (3, -2).
More about the linear equation link is given below.
https://brainly.com/question/11897796
#SPJ2
Sasha counts unit squares to find the area of the rectangle. What is another way she could find the area?
Answers
Answer:
- Take the length and width, and multiply
Step-by-step explanation:
Which numbers can this composite number be divided by? Select all that apply.
9
Answers
Answer:
3
Step-by-step explanation:
Please help me with this question. I will give you 30 points and I will drop a picture here! Please help ASAP.

Answers
Bos Ross amount in commission is 3276 dollars.
Bos Ross gross pay is 5346 dollars.
How to find the amount of commission and gross pay?Washington plastic product pays Bob Ross a 2070 dollars monthly salary plus 4% commission on merchandise he sells each month.
Bob sales were 81900 last month. Therefore, let's calculated his commission and gross pay.
Therefore,
commission = 4% of 81900
commission = 4 / 100 × 81900
commission = 4 × 819
commission = 3276 dollars
Hence, let's find his gross pay
Gross pay = monthly salary + commission
monthly salary = 2070 dollars
commission = 3276 dollars
Gross pay = 2070 + 3276
Gross pay = 5346 dollars
learn more on commission here: https://brainly.com/question/23884487
#SPJ1
Jack bought 1 3/4 pounds of pork and 2 3/4 pounds of beef.
How many pounds of meat did John buy in all?
Answers
Answer:
4 1/2 pounds of meat
Step-by-step explanation:
if you have 2 adding fractions with 3 quarters just add it like 1 1/2 + 2 1/2 and add half to your final answer
A parallelogram is drawn on a
coordinate plane so that three vertices
are located at these coordinates: (-1,2), (1,2), and (-1,-3). What are the coordinates of the fourth
vertex of the parallelogram?
Answers
Answer:
(-3 , -3)
Step-by-step explanation:
A: (-1,2), B: (1,2), and C: (-1,-3) .... D: (x,y)
slope of AB = (2-2)/(1 - -1) = 0 .... parallel to x axis
x coordinate of A is 2 units left to B (-1 vs 1)
y coordinate of C is 2 units left to B so D must be 2 units left to C: -1 -2 = -3
DC // AB , y coordinate of D = C = -3
D: (-3 , -3)

Please help.
Is algebra.

Answers
Answer:
(-4, 1)
Step-by-step explanation:
Answer:
Step-by-step explanation:
The solution is the point where the two lines intersect each other, in this case
(-4,1)
Meaning
x=-4 and y=1