Answers
Answer:
127°
Step-by-step explanation:
The equation is
13x-25=9x-1
4x=24
x=6
So
M angle D=127
Related Questions
Find the lateral surface area of the figure.
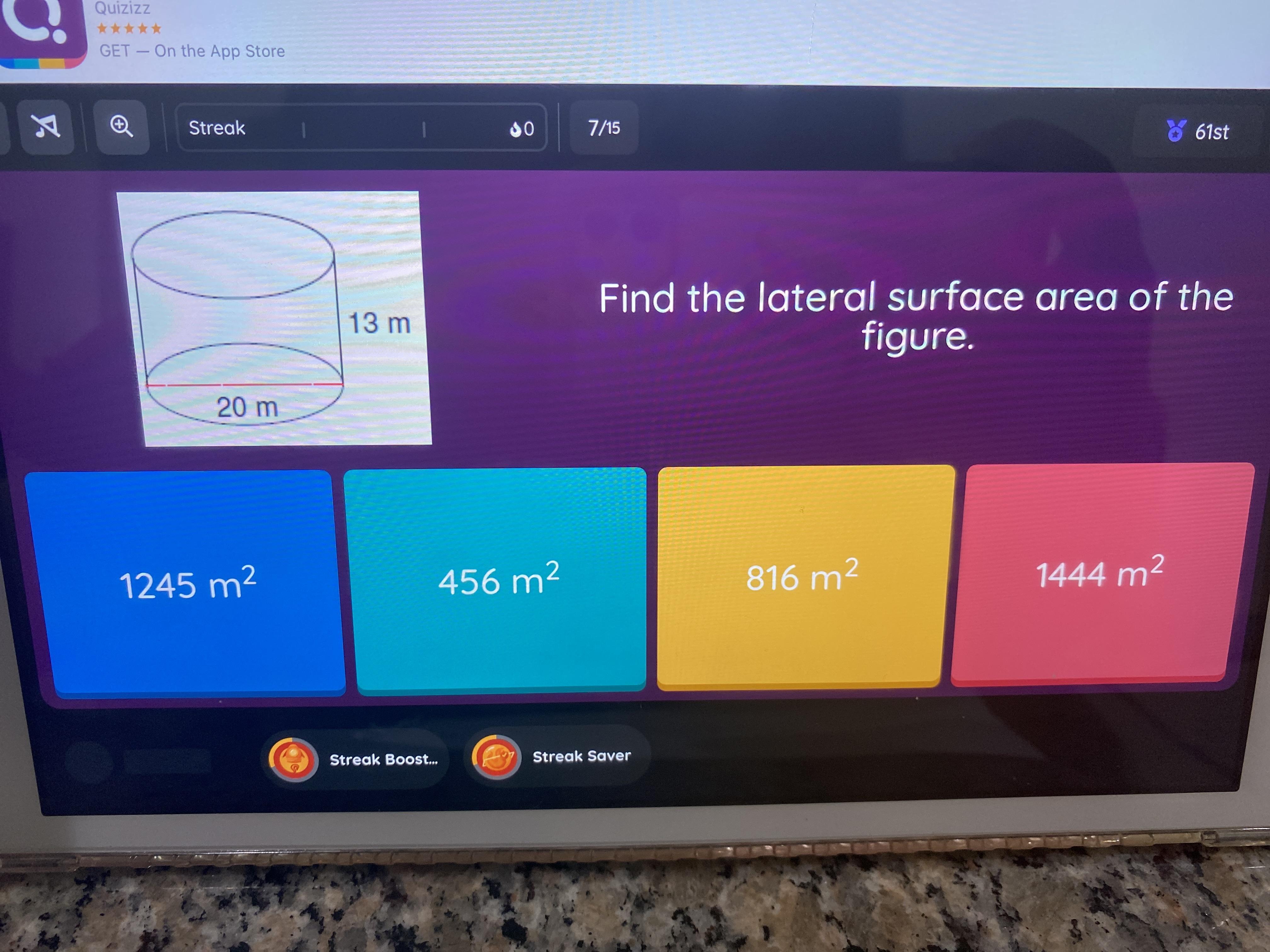
Answers
The evaluated lateral surface area is 261.8 square meters, under the condition that the base length is 20 m and height is 13 m.
The lateral surface area of a cylinder is given by the formula 2πrh
Here,
r = radius of the base
h = height of the cylinder.
For the given case, the base length is 20 m and height is 13 m. Then the base length is stated instead of the radius, we have to evaluate the radius first.
The radius of a cylinder can be found applying the formula r = l/2π
Here,
l = base length.
So, staging l = 20 m
, we get
r = 20/(2π)
≈ 3.18 m
Now that we have received the radius and height, we can evaluate the lateral surface area applying the formula mentioned above.
Staging
r = 3.18 m
h = 13 m,
we get:
Lateral surface area
= 2πrh
≈ 261.8 m²
Then, the lateral surface area of the given cylinder is approximately 261.8 square meters.
To learn more about surface area
https://brainly.com/question/951562
#SPJ1
If x and y are variables and b and m are constants, which of these functions is linear? Assume that m = 0. A y = mx + b B y=mx? + 6 C y = m + b D y=x" + 6
Answers
Answer:
The answer is c
Step-by-step explanation:
YO 5 OR 22 POINTS CAN SOMEBODY MAKE A GRAPH OF THIS. PLS HELP IM STUCK

Answers

Select the correct answer. What is the equation of the line that has a slope of 3 and goes through the point (-3,-5)? A. y = 3x + 4 B. y = 3x − 14 C. y = 3x − 4 D. y = 3x + 12
Answers
Equation of line in point slope form
\(\\ \sf\longmapsto y-y1=m(x-x1)\)
\(\\ \sf\longmapsto y+5=3(x+3)\)
\(\\ \sf\longmapsto y+5=3x+9\)
\(\\ \sf\longmapsto y=3x+4\)
In which diagram do angles 1 and 2 form a linear pair?
2 lines intersect and form 4 angles. Labeled clockwise from the top: blank, 2, blank, 1.
3 lines extend from a point and form 2 angles, labeled 1 and 2. Both angles add up to 90 degrees.
A horizontal line has 2 lines extending from a midpoint forming 3 angles. Labeled from left to right: 1, 2, 3.
A horizontal line has 1 line extending from it. Angles 1 and 2 are formed.
Mark this and return
Answers
The diagram where angles 1 and 2 form a linear pair is option D which is that a horizontal line has 1 line extending from it. Angles 1 and 2 are formed.
Given that angle 1 and 2 form a linear pair.
We know that a linear pair is an angle that are formed when two lines intersect each other at a single point.
In our case when a horizontal line has 1 line extending from it and when angles 1 and 2 are formed shows a linear pair.
In first part when two lines intersect they donot form 4 angles.
In second part when 3 lines extend from a point they don't form right angle between the lines.
Hence the linear pair angles are shown by the statement that a horizontal line has 1 line extending from it. Angles 1 and 2 are formed.
Learn more about linear pair angles at https://brainly.com/question/13218054
#SPJ1
right rectangular prism calc: find w, l=n/a, h=n/a, v=n/a
Answers
The value of width 'w' of rectangular prism with l = n/a, h = n/a, v = n/a is given by, w = a/n.
We know that the volume of rectangular prism with length L and width W and Height H is given by,
V = L*W*H
Given that the Height of the rectangular prism, h = n/a
Length of the rectangular prism, l = n/a
Volume of the rectangular prism, v = n/a
let the width of the rectangular prism be 'w'.
So from the volume formula we get,
v = lwh
n/a = (n/a)*w*(n/a)
n/a = (n/a)²*w
w = (n/a)/(n/a)² = (n/a)*(a/n)² = a/n
Hence the value of w is a/n.
To know more about rectangular prism here
https://brainly.com/question/30095130
#SPJ4
if jane walks north for 3 miles, turns $45^\circ$ to the right, and then walks another 4 miles, how many miles will jane be from her starting point? give your answer as a decimal rounded to the nearest hundredth. (you may use a calculator to compute the approximation.)
Answers
.Find the area of the region that lies under the parabola y=5x - x^2, where 1≤x≤4.
Answers
The area of the region under the parabola y = 5x - x^2, where 1 ≤ x ≤ 4, is 14.33 square units.
To find the area under the parabola, we need to integrate the equation y = 5x - x^2 with respect to x over the given interval [1, 4]. The integral represents the area between the curve and the x-axis.
Integrating y = 5x - x^2 gives us the antiderivative F(x) = (5/2)x^2 - (1/3)x^3 + C, where C is the constant of integration. To find the definite integral over the interval [1, 4], we evaluate F(4) - F(1).
F(4) = (5/2)(4)^2 - (1/3)(4)^3 + C = 40 - (64/3) + C
F(1) = (5/2)(1)^2 - (1/3)(1)^3 + C = 5 - (1/3) + C
Substituting these values into the definite integral expression, we have:
Area = F(4) - F(1) = (40 - (64/3) + C) - (5 - (1/3) + C)
= 14.33
The area of the region under the parabola y = 5x - x^2, where 1 ≤ x ≤ 4, is approximately 14.33 square units.
To know more about parabola, visit;
https://brainly.com/question/12793264
#SPJ11
9000÷20=N ????? pls answer
Answers
To get the value of N let's do the division.
The value of N is 450

Solve the following three equations



Answers
Answer:
2 sq rt 33
Step-by-step explanation:
1st step: subtract one, each side
(radical 2/3)r = 22
2nd step: set up a proportion
(radical 2/3)r = 22
3rd step: cross-multiply
radical 2*r = 66
4th step: solve for 'r'
r = 66 / radical 2
5th step: rationalize the denominator
multiply numerator and denominator by radical 2
6th step: simplify
(66\(\sqrt{2}\)) / 2 = 33 \(\sqrt{2}\)
Jonathan has 25 coins in his pockets and they are all either nickels or quarters. If he has a total of
$3.25, how many of the coins are nickels and how many are quarters. Give me two equations and the answer in nickels and quarters
Answers
Answer:
The answer is 10 quarters and 15 nickels
Step-by-step explanation:
Lets say x equals the number of quarters and y quals the number of nickels. Since there is a total of 25 coins that means that x+y=25. But, the quarter costs 0.25, and the nickel costs 0.05. That means that we have to multiply the number of each coin with their cost. Which leads us to: (x*0.25)+(y*0.05)=3.25. By solving these two equations you'll see that x=10 and y=15.
Henry has 2 six-sided number cubes, one red, and one blue. The faces of the red cube are numbered 1-6. The faces of the blue cube are numbered 7-12. If Henry tosses both number cubes, what is the probability that the sum of the two cubes will be a prime number? Show and explain how you got your answer.
Answers
Answer:
babylonia and lseral i thik so
The probability that the sum of the two cubes will be a prime number is 0.33.
What is Probability?Probability is simply the possibility of getting an event. Or in other words, we are predicting the chance of getting an event.
The value of probability will be always in the range from 0 to 1.
Given that,
Henry has 2 six-sided number cubes, one red, and one blue.
The faces of the red cube are numbered 1-6.
The faces of the blue cube are numbered 7-12.
Henry tosses both number cubes.
Sample space for the experiment = {(1, 7), (1, 8), .........., (1, 12), (2, 7), (2, 8), ......., (2, 12), .........., (6, 7), ...........,(6, 12)}
Total number of outcomes = 36
Least sum is 1 + 7 = 8 and greatest sum is 6 + 12 = 18
Prime numbers in between 8 and 18 are 11, 13 and 17.
Sum will be prime numbers for the outcomes,
{(1, 10), (1, 12), (2, 9), (2, 11), (3, 8), (3, 10), (4, 7), (4, 9), (5, 8), (5, 12), (6, 7), (6, 11).
Number of outcomes which sum are prime numbers = 12
Probability = 12/36 = 1/3 = 0.333
Hence the probability is 0.33.
Learn more about Probability here :
https://brainly.com/question/30034780
#SPJ3
The function f(x) is graphed below. What is the value of f(-2)?

Answers
Answer:
f(-2) = 4
Step-by-step explanation:
Looking at the graph, at -2 the graph is at the point (-2,4). Therefore, the value of f(-2) is 4.
How many people should we book for each flight?
PLEASE HELP DKSVBSKSBS

Answers
How would you find the distance between these two points? Would the negative coordinate have any effect on your calculation? A. The negative coordinate would not have an impact on the distance since distance is always positive - absolute value, so you would subtract 4 - 3 to get the distance. B. The negative coordinate would have an impact on the distance, so you would add -4 + 3 to get the distance. C. The negative coordinate would not have an impact on the distance since distance is always positive - absolute value, so you would add 4 + 3 to get the distance. D. The negative coordinate would have an impact on the distance, so you would subtract -4 - 3 to get the distance.
Answers
In the scenario, C. The negative coordinate would not have an impact on the distance since the distance is always positive - absolute value, so you would add 4 + 3 to get the distance.
What is an integer?Integer numbers can be positive or negative, and the addition is determined by the signal, as seen below:
We preserve the signal and add the values if they both have the same signal.
If they have different signals, we add the signal of the word with the higher absolute value.
The distance between two points is calculated by subtracting their absolute values. For this problem, we need to calculate the distance between points -4 and 3, so:
3 - (-4) = 3 + 4 = 7.
Therefore, the correct option is C.
Learn more about coordinate on:
https://brainly.com/question/28790514
#SPJ1
help meh pls i give brainiest

Answers
numbers:
2, 4, and 5
I am so sorry if i'm wrong!!! :|
Bert and Ernie are solving the inequality 2x²+5x-3
problem 3-67 when Bert has an idea. "Can't we change this into one parabola and solve our
inequality that way?", he asks.
Ernie asks, "What do you mean?"
"Can't we determine the solutions by looking at the graph of f(x)=x²+x-6?", Bert replies.
a. Where does Bert get the equation f(x)=x²+x-6?
b. Try Bert's idea. Make a sketch of the parabola and show how it can be used to solve the
original inequality.
Answers
Answer:
Step-by-step explanation:
Given equation: f(x)=x^2+x-6
The roots of the equation, set the equation equal to zero.
\(x^2+x-6=0\\x^2+3x-2x-6=0\\x(x+3)-2(x+3)=0\\ (x+3)(x-2)=0\\ x=-3,2\)
Therefore, the roots of the equation are x=-3 and x=2
suppose that a die is made by marking the faces of a regular dodecahedron with the numbers 1 through 12. what is the probability that on exactly three of six tosses, a number less than 4 turns up?
Answers
Suppose that a die is made by marking the faces of a regular dodecahedron with the numbers 1 through 12. We are to determine the probability that on exactly three of six tosses, a number less than 4 turns up.
We note that the sum of the numbers on the faces of the die is 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78. Thus the expected value of the face is E(X) = (1 + 2 + 3 + ... + 12)/12 = 78/12 = 6.5.
To compute the probability that on exactly three of six tosses, a number less than 4 turns up, we use the binomial distribution with n = 6 and p = 3/12 = 1/4. The probability that on exactly three of six tosses, a number less than 4 turns up is P(X = 3) = (6 choose 3)(1/4)^3(3/4)^3= 20(1/64)(27/64)= 27/160 or 0.169.
So, the required probability that on exactly three of six tosses, a number less than 4 turns up is 27/160 or 0.169.
To know more about dodecahedron visit:
https://brainly.com/question/12773715
#SPJ11
Y’all I’m confused, help

Answers
Answer:
4^3 Expantion: (4)(4)(4) evaluated: 64
-2^4 Expantion: -(2)(2)(2)(2) evaluated: -16
(-3)^3 Expantion: (-3)(-3)(-3) Evaluated: -27
(-7)^3 Expantion: (-7)(-7)(-7) Evaluated: -343
PLEASE HELP!! The cost for parking in the local covered parking lot is calculated by ƒ(h) = 4.5 + 1.5⌈(h - 1)⌉ where h is the number of hours you parked. What is the cost for parking in the garage for 75 minutes?
Answers
Answer:
The cost of parking in the garage for 75 minutes is 4.875.
Step-by-step explanation:
The costs of parking h hours is given by the following function:
\(f(h) = 4.5 + 1.5(h-1)\)
Cost of parking 75 minutes.
1 hour is 60 minutes. How many hours are 75 minutes?
1h - 60 min
xh - 75 min
\(60x = 75\)
\(x = \frac{75}{60}\)
\(x = 1.25\)
75 minutes is 1.25 hours. So we have to find f(1.25).
\(f(1.25) = 4.5 + 1.5*(1.25-1) = 4.875\)
The cost of parking in the garage for 75 minutes is 4.875.
What is the solution set?
−2.8x+5.6<8.4
Answers
Answer:
x>−1
Step-by-step explanation:
−2.8x+5.6<8.4
Subtract 5.6 from both sides.
−2.8x<8.4−5.6
Subtract 5.6 from 8.4 to get 2.8.
−2.8x<2.8
Divide both sides by −2.8. Since −2.8 is negative, the inequality direction is changed.
x> −2.8 / −2.8
Divide 2.8 by −2.8 to get −1.
x>−1
Answer: X is less than -1
Step-by-step explanation:
Given AE and BD bisect each other at point c, which congruence theorem would you use to prove triangle ABC =~ triangle EDC ?

Answers
Explanation:
AC = EC
BC = DC
angle ACB = angle DCE (Vertically Opposite Angles)
Therefore, the triangles are congruent by the Side-Angle-Side congruency
Juan is shopping for school supplies. He bought a pencil case for $5.00, but now he needs
pencils to go inside it. Each box of pencils $3.00. Let t represent the total cost, and b represent
each box of pencils. Determine the dependent and independent variables.
Answers
Answer:
T is dependent B is independent
Step-by-step explanation:
Total cost is changed by how many pencils you buy
The price of each box of pencils does not change
I will report you for any not serious answers, and the points will be taken away from you.
I have the answer of 8 for x, but does 3 WORK for x?
Because my answer choices consists of 24, but not 8.
My big question is "is 3 a valid solution"

Answers
Answer:
i don't think 3 works for x because the only solution for x was 8
Step-by-step explanation:
Find two numbers whose difference is 92 and whose product is a minimum.
Answers
Step-by-step explanation:
x -y = 92 x = 92+y
xy = minumum
(92+y) * y = minumum
y^2 + 92y = minumum this quadratic has a minimum at
y = -b/2a = - 92/(2*1) = - 46
x - -46 = 92 shows x = +46 minimum is then - 2116
pls help me for question no.4

Answers
Answer:
Area of the composite figure = 75.25 cm²
Step-by-step explanation:
Question (4). Given figure is a composite figure having,
(1). Right triangle STU
(2). A kite PSUV
(3). A trapezoid PQRS
Now we will calculate the area of each figure.
(1). Area of the right triangle = \(\frac{1}{2}(\text{ST})(\text{TU})\)
= \(\frac{1}{2}(3.5)(3)\)
= 5.25 cm²
(2). Area of the kite PSUV = \(\frac{1}{2}(\text{Diagonal 1})(\text{Diagonal 2})\)
= \(\frac{1}{2}(\text{PU})(\text{SV})\)
= \(\frac{1}{2}(\text{TS+RQ})(\text{SV})\)
= \(\frac{1}{2}(3.5+7)(6)\) [Since SV = 2 × 3 = 6 cm]
= \(3\times 10.5\)
= 31.5 cm²
(3). Area of the trapezium = \(\frac{1}{2}(b_1+b_2)(h)\) [Where \(b_1\) and \(b_2\) are the bases and h is the distance between the bases]
= \(\frac{1}{2}[(7-3)+7](7)\)
= \(\frac{77}{2}\)
= 38.5 cm²
Total area of the given figure = 5.25 + 31.5 + 38.5
= 75.25 cm²

a building casts a 103-foot shadow at the same time that a 32-foot flagpole casts as 34.5-foot shadow. how tall is the building in feet?
Answers
The height of the the building is 95.5 feet.
As per the given data:
A building casts a 103-foot shadow.
At the same time, a 32-foot flagpole casts a 34.5-foot shadow.
Diagrams of both the building and flagpole are attached at the end of the solution.
Here we have to determine the height of the building.
From the above figure, in Δ ABC, AB shows the height of the building and BC shows its shadow length. In ΔDEF, DE shows the height of the flagpole and EF shows its shadow length.
In ΔABC
\($ \tan \theta=\frac{A B}{B C} \\\)
\($& \tan \theta=\frac{A B}{103}\)
In ΔDEF
\($& \tan \theta=\frac{D E}{E F} \\\)
\($\tan \theta=\frac{32}{34.5}\)
At the same time, the angle of elevation of the sun is the same at all the places.
Therefore
\($& \tan \theta=\tan \theta \\\)
\($& \frac{A B}{103}=\frac{32}{34.5} \\\)
\($& AB = \frac{32 \times 103}{34.5} \\\)
A B = 95.5 foot
Therefore, the height of the building will be 95.5 feet.
For more questions on heights in trigonometry
https://brainly.com/question/7453947
#SPJ4

Can someone please help me with question 24?

Answers
Answer: (d) 270
Step-by-step explanation:
10 out of 18 people have a motorcycle(which simplifies to 5/9 people) therefore
486 x 5/9 = 270 people have a motorcycle.
Answer:
270
Step-by-step explanation:
All you have to do is divide 486 by 18 and thats when you get 27 and then multiple 10 by 27.
can someone please help me solve these math problems they are about triangle proofs

Answers
Answer:
Besides the givens:
12.
AC = EC, BC = DC; Definition of Midpoint
<ACB = <ECD; Vertical Angles Theorem
Triangle ABC = Triangle EDC; SAS Congruence Postulate
13.
AD = CD; Definition of Median
BD = BD; Reflexive Property
Triangle ABD = Triangle CBD; SSS Postulate
Step-by-step explanation:
None necessary.
Q3. The given coordinates are (0,0), (0,2),(2,0),(2,2) for
representing a rectangle/square ,you are expected to find
x-shearing where shearing parameter towards x-direction is 2 units.
Also you are ex
Answers
After the x-shearing transformation, the resulting coordinates of the rectangle/square are: (0,0), (0,2), (2,0), and (2,6). This transformation effectively shears the shape by shifting the y-coordinate of the top-right corner, resulting in a distorted rectangle/square.
To apply x-shearing with a shearing parameter of 2 units to a rectangle/square defined by the coordinates (0,0), (0,2), (2,0), and (2,2), we can transform the coordinates as follows: (0,0) remains unchanged, (0,2) becomes (0,2), (2,0) becomes (2,0), and (2,2) becomes (2,6). This transformation effectively shifts the y-coordinate of the top-right corner of the rectangle by 4 units while leaving the other coordinates unchanged, resulting in a sheared shape.
X-shearing is a transformation that shifts the y-coordinate of each point in an object while leaving the x-coordinate unchanged. In this case, we are given a rectangle/square with coordinates (0,0), (0,2), (2,0), and (2,2). To apply x-shearing with a shearing parameter of 2 units, we only need to modify the y-coordinate of the top-right corner.
The original coordinates of the rectangle/square are as follows: the bottom-left corner is (0,0), the top-left corner is (0,2), the bottom-right corner is (2,0), and the top-right corner is (2,2).
To perform the x-shearing, we only need to modify the y-coordinate of the top-right corner. The shearing parameter is 2 units, so we shift the y-coordinate of the top-right corner by 2 * 2 = 4 units. Therefore, the new coordinates of the rectangle/square become: (0,0) remains unchanged, (0,2) remains unchanged, (2,0) remains unchanged, and (2,2) becomes (2,2 + 4 = 6).
After the x-shearing transformation, the resulting coordinates of the rectangle/square are: (0,0), (0,2), (2,0), and (2,6). This transformation effectively shears the shape by shifting the y-coordinate of the top-right corner, resulting in a distorted rectangle/square.
Learn more about parameter click here: brainly.com/question/30931527
#SPJ11
