Answers
Answer:
The correct answer is A
Step-by-step explanation
Related Questions
Which of the following are true when considering the probability of spinning a multiple of 5 on an equal section spinner with numbers 1-20? Check all that apply.
P(A)=20%
P(A
′
)=0.8
n(A
′
)=16
A={5,10,15,20}
P(A)=4/20
n(S)=20
P(A)=1/5
P(A
′
)=4/5
S is all numbers between 1 and 20 inclusive n(A)=4
Answers
We are given a spinner with equal sections numbered from 1 to 20. The question is about the probability of spinning a multiple of 5. We need to determine which statements are true regarding this probability.
P(A) = 20%: This statement is false. The probability of spinning a multiple of 5 is not 20% because there are four multiples of 5 (5, 10, 15, and 20) out of 20 possible outcomes.
P(A') = 0.8: This statement is false. P(A') represents the probability of not spinning a multiple of 5. The correct probability would be P(A') = 1 - P(A) since it includes all outcomes not in A.
n(A') = 16: This statement is true. n(A') represents the number of outcomes not in A, which is 16 (20 - 4 = 16).
A = {5, 10, 15, 20}: This statement is true. A is the set of outcomes representing the multiples of 5 on the spinner.
P(A) = 4/20: This statement is true. There are four favorable outcomes (multiples of 5) out of a total of 20 possible outcomes, giving a probability of 4/20.
n(S) = 20: This statement is true. n(S) represents the total number of outcomes in the sample space, which is 20 in this case.
P(A) = 1/5: This statement is false. The probability of spinning a multiple of 5 is 4/20, not 1/5.
P(A') = 4/5: This statement is true. P(A') represents the probability of not spinning a multiple of 5, which is 16/20 or 4/5.
In conclusion, the true statements regarding the probability of spinning a multiple of 5 on the spinner are: n(A') = 16, A = {5, 10, 15, 20}, P(A) = 4/20, n(S) = 20, and P(A') = 4/5.
Learn more about Probability here :
brainly.com/question/30034780
#SPJ11
area of a circle pls help fast
Answers
The area of a circle is the measure of the surface enclosed by the circle. It is given by the formula A = πr², where A is the area, π (pi) is a mathematical constant approximately equal to 3.14, and r is the radius of the circle.
To calculate the area of a circle, you need to know the value of its radius. The radius is the distance from the center of the circle to any point on its edge. Once you have the radius, simply plug it into the formula and solve for A.
For example, if the radius of a circle is 5 units, the area can be calculated as follows:
A = πr²
A = π(5)²
A = π(25)
A = 78.5 (rounded to one decimal place)
Therefore, the area of the circle with a radius of 5 units is approximately 78.5 square units.
It is worth noting that the area of a circle is proportional to the square of its radius. This means that if you double the radius, the area will increase by a factor of four. Similarly, if you halve the radius, the area will decrease by a factor of four. In summary, the area of a circle is given by the formula A = πr², where A is the area and r is the radius. To calculate the area, simply plug in the value of the radius and solve for A.
To know more about surface visit:-
https://brainly.com/question/28267043
#SPJ11
A line passes through the points (1, -6) and (4,3). What is the y-intercept of this line?
○ -9
○ -3
○ 3
○ 9

Answers
Answer: -9
In the production possibilities framework, economic growth is depicted by the PPF Group of answer choices becoming a straight line rather than a bowed outward curve. shifting leftward (toward the origin). becoming bowed outward rather than a straight line. shifting rightward (away from the origin).
Answers
In the production possibilities framework, economic growth is depicted by the PPF (Production Possibilities Frontier) shifting rightward (away from the origin). This indicates an increase in the economy's capacity to produce goods and services.
The production possibilities framework represents the different combinations of goods and services that an economy can produce given its resources and technology.
The PPF is typically depicted as a curve, showing the trade-off between producing different goods or allocating resources between different sectors of the economy.
When the PPF shifts rightward, it means that the economy's production capacity has increased.
This can happen due to various factors such as technological advancements, increased capital investment, improved infrastructure, or an expansion of the labor force.
As a result, the economy can produce more goods and services at each point along the PPF.
The shift of the PPF rightward indicates economic growth because it signifies an expansion of the production possibilities.
With a larger production capacity, the economy has the potential to achieve higher levels of output, leading to increased living standards, higher incomes, and greater overall economic prosperity.
On the other hand, if the PPF became a straight line or shifted leftward (toward the origin), it would indicate a decrease in the economy's production capacity or a decline in resources or technology.
In such cases, the economy would experience a contraction in its production possibilities and potentially face challenges in meeting the needs and wants of its population.
Therefore, the correct answer is that economic growth in the production possibilities framework is depicted by the PPF shifting rightward (away from the origin).
Learn more about economic growth here:
https://brainly.com/question/29571333
#SPJ11
find p where f(x) = 2x ^ 3 + 5x ^ 2 + px + 8 where f(- 2) = 10
Answers
Explanation
Given the function
\(f\mleft(x\mright)=2x^3+5x^2+px+8\)We can find the value of p when f(-2 )=10 below;
Therefore, we will have;
\(\begin{gathered} f(-2)=2(-2)^3+5(-2)^2+(-2)p+8=10 \\ -16+20-2p+8=10 \\ -4-2p+8=10 \\ -2p+4=10 \\ -2p=10-4 \\ -2p=6 \\ p=\frac{6}{-2} \\ p=-3 \end{gathered}\)Answer: p = -3
A watering can contained 5 ½ quarts water. After all the plants were watered, only 4 cups remained.
How many cups of water were used to water the plants?
7 cups
18 cups
40 cups
84 cups
Answers
Answer: 18 cups
Step-by-step explanation:
Answer:
the answer is 18 cups :))
a) A recipe calls for 2 cups of sugar and 3 cups of flour. If you want to make 12 cups mixture, how many cups of sugar and flour will you need?
b) The ratio of the angles of a triangle is 2:3:5. What is the measure of the smallest angle in the triangle?
Answers
number a should given any of the clues. It does not make any sense.

solve the given initial-value problem. dy/dt 2(t+1)y2 = 0, y(0) = − 1/15 y(t) = 1/t^2 + 2t + 15Give the largest interval i on which the solution is defined. (enter your answer using interval notation.)
Answers
The largest interval on which the solution is defined is (-∞, -1) ∪ (-1, ∞). The interval notation for the largest interval is (-∞, -1) U (-1, ∞).
What is the initial-value problem?An initial-value problem is a type of boundary-value problem in mathematics, particularly in the field of differential equations.
The given initial-value problem is a separable differential equation, which can be written as:
dy/dt = -2(t + 1)y²
Integrating both sides, we get:
(1/y) = t² + 2t + C
where C is the constant of integration.
Since we have an initial condition, we can use it to find the value of C:
y(0) = -1/15
C = -1/15
Solving for C, we get:
C = -1/15
So, the solution to the differential equation is:
(1/y) = t² + 2t -1/15
y = 1 / (t² + 2t -1/15)
The solution is defined for all t ≠ -1, since y = 0 is not defined. So, the largest interval on which the solution is defined is (-∞, -1) ∪ (-1, ∞). The interval notation for the largest interval is (-∞, -1) U (-1, ∞).
Learn more about the initial value problem here:
https://brainly.com/question/30503609
#SPJ1
Express this |-3x-4|
Answers
A popular magazine tests cars and trucks for mileage on the road and around the city. The magazine reports that the most common gas mileage was 24 mpg. Which statistic does this 24 represent
Answers
It shows that the values of the mileages are close to 24 mpg. Hence statistics refes 24 as the mean.
Mean of a data.Mean is one of the measure of dispersion and is the avearage of a set of data.
According to the question, the magazine reports that the most common gas mileage was 24 mpg. This shows that reports have published several gas mileages for cars and truck and the average of this mileage is 24mpg
It shows that the values of the mileages are close to 24 mpg. Hence statistics refes 24 as the mean.
Learn more on mean here: https://brainly.com/question/14532771
#SPJ1
Find the distance between P(3,2) and Q(6,7).
Answers
Answer:
Step-by-step explanation:
For example, we have a coordinate grid below as shown.
If you count the units you will get a number around 7.
The graph attached shows the position of a race car as it tests out a new engine.
a. What is the distance traveled by the car between 1 and 9 seconds?
b. What is the average speed of the car between 1 and 9 seconds? (Answer in km/s.)
c. Describe how the speed of the car changes throughout its test run.
d. If you had a graph of velocity versus time for this test, what would be the total area under the curve?
Please show all work

Answers
a) The distance traveled by the car is 240 km, b) the average speed of the car is 30 km/s, c) the speed of the car changes from increasing to constant to decreasing, d) and the total area under the curve 240 km/s.
a. To find the distance traveled by the car between 1 and 9 seconds, we need to find the area under the curve of the velocity-time graph between 1 and 9 seconds. By counting the number of squares, we can estimate the area to be approximately 24 square units. Since each square represents a velocity of 10 km/h and the time interval is 8 seconds, the distance traveled by the car is approximately 240 km.
b. The average speed of the car between 1 and 9 seconds is equal to the total distance traveled divided by the time taken, which is 240 km / 8 s = 30 km/s.
c. The speed of the car increases from 0 km/h to 60 km/h in the first 2 seconds, then remains constant at 60 km/h for the next 6 seconds, and finally decreases to 0 km/h in the last 2 seconds. Therefore, the speed of the car changes from increasing to constant to decreasing throughout its test run.
d. If we had a graph of velocity versus time for this test, the total area under the curve would represent the total displacement of the car, which is equal to the distance traveled in this case. Since the area under the curve is a trapezoid, we can calculate it as the average of the two parallel sides multiplied by the height, which is (0 + 60) / 2 x 8 = 240 km/s.
To learn more about distance please click on below link
https://brainly.com/question/2734924
#SPJ1
Two numbers are in ratio 3 by 2 and their difference is 5 find numbers
Answers
Answer:
15,10
Step-by-step explanation:
let the numbers be 3x and 2x
3x-2x=5
x=5
∴ numbers are 3×5,2×5
or 15,10
Assume an exponential function has a starting value of 16 and a decay rate of 4%. Write an equation to model the situation.
Answers
Nadine has a plastic container in the shape of a prism that is filled with beads. The container has a length of 6 inches, a width of 8 inches, and a height of
5 inches
The container has a crack, so she needs to move all of the beads to new containers that are also rectangular prisms. Determine which sets of containers she could use for
the beads.
Select Yes or No for each set of containers.

Answers
Answer:
BTW C= containers and AC = area of all the containers all together.
Step-by-step explanation:
So first off you calculate the area of the container that had a crack so its
Width X Length X height | 6 x 8 x 5 = 240
So then you look at the possible answers and then calculate the area of those plastic containers. So then you start with the first one and it would be like this
First possible answer: 3 and 1/3 x 6 x 5 = 100 x 3c = 300ac
Second possible answer: 2 and 1/4 x 4 and 3/4 x 6 = 64.125 x 4c = 256.5ac
Third possible answer: 3.5 x 6.5 x 6 = 136.5 x 2c = 273ac
Fourth possible answer: 3 and 1/2 x 3 and 1/4 x 5 = 56.875 x 5c = 284.375ac
Hopefully this will help you find your answer!! I tried my best!! Please give brainly!!
diego brought a box of 120 colored pencils to school. he gave 14 pencils to marcus and 32 pencils to anna. how many pencils did diego have left
Answers
Diego will have 74 pencils remaining after giving 14 pencils to Marcus and 32 pencils to Anna.
The question is about simple Subtraction. First, we know that the total number of colored pencils in the box is 120. Following is the step-by-step explanation for this question.
Let suppose,
Total Colored pencils = x = 120
Pencils given to Marcus = y = 14
Pencils are given to Anna = z = 34.
And, Total Pencil Remaining = R =?
We can show the given information in the equation as given below:
R = x - y - z
By putting the value in the above equation:
R = 120 - 14 -34
R = 74.
So, after giving the 14 and 32 pencils to Marcus and Anna, respectively. Marcus would remain with 74 Pencils.
To learn more about Subtraction, click here
brainly.com/question/27351494
#SPJ4
…………………………………………………2x-3(x+1)
Answers
Answer:
-1x+3 or -x+3
Step-by-step explanation:
2x-3(x+1)
2x-3x+3
-1x+3 or -x+3
What is the coefficient of the second term in this expression?
4+5c
Answers
Answer:
The coefficient of the second tern in the expression , 4+ 5c, is 5
Step-by-step explanation:
Second term: 5c
C is a variable,therefore, making 5 the coeffiecient.
Mrs. Rodriquez is purchasing trophies for each child that plays little league. She wants to spend no more than $7.00 per trophy. Which of the following purchases will satisfy her budget?
Answers
Answer:
Mrs. Rodriquez is purchasing trophies for each child that plays little league. She wants to
spend no more than $7.00 per trophy. Which of the following purchases will satisfy her budget?
Select all that apply.
A. 3 trophies for $24.00
B. 5 trophies for $30.00
C. 7 trophies for $49.00
D. 9 trophies for $72.00
E. 12 trophies for $96.00
Step-by-step explanation:
help for brainist plez

Answers
Answer:
the answer is D
Step-by-step explanation:
i explain it here

Answer:
the answer is d
Step-by-step explanation:
2. find f(1), f(2), f(3), f(4), and f(5) if f(n) is defined re- cursively by f(0) = 3 and for n = 0, 1, 2, … a) f(n + 1) = −2f(n). b) f(n + 1) = 3f(n) + 7. c) f(n + 1) = f(n)2 − 2f(n) − 2. d) f(n + 1) = 3f(n)∕3.
Answers
Here are the values of f(1), f(2), f(3), f(4), and f(5) for each recursive definition:
a) \(\[f(1) = -6, \quad f(2) = 12, \quad f(3) = -24, \quad f(4) = 48, \quad f(5) = -96\]\)
b) \(\[f(1) = 16, \quad f(2) = 55, \quad f(3) = 172, \quad f(4) = 523, \quad f(5) = 1576\]\)
c) \(\[f(1) = 1, \quad f(2) = -3, \quad f(3) = 11, \quad f(4) = 107, \quad f(5) = 11365\]\)
d) \(\[f(1) = 3, \quad f(2) = 3, \quad f(3) = 3, \quad f(4) = 3, \quad f(5) = 3\]\)
a) Recursive definition: \(\(f(n + 1) = -2f(n)\)\)
To find \(\(f(1)\)\), we use the initial condition \(\(f(0) = 3\)\) and apply the recursive definition:
\(\[f(1) = -2f(0) = -2 \cdot 3 = -6\]\)
To find \(\(f(2)\)\):
\(\[f(2) = -2f(1) = -2 \cdot (-6) = 12\]\)
Similarly, we can continue applying the recursive definition to find \(\(f(3)\), \(f(4)\), and \(f(5)\)\):
\(\[f(3) = -2f(2) = -2 \cdot 12 = -24\]\)
\(\[f(4) = -2f(3) = -2 \cdot (-24) = 48\]\)
\(\[f(5) = -2f(4) = -2 \cdot 48 = -96\]\)
b) Recursive definition: \(\(f(n + 1) = 3f(n) + 7\)\)
Using the initial condition \(\(f(0) = 3\):\)
\(\[f(1) = 3f(0) + 7 = 3 \cdot 3 + 7 = 16\]\)
To find \(\(f(2)\)\):
\(\[f(2) = 3f(1) + 7 = 3 \cdot 16 + 7 = 55\]\)
Continuing in the same manner:
\(\[f(3) = 3f(2) + 7 = 3 \cdot 55 + 7 = 172\]\)
\(\[f(4) = 3f(3) + 7 = 3 \cdot 172 + 7 = 523\]\)
\(\[f(5) = 3f(4) + 7 = 3 \cdot 523 + 7 = 1576\]\)
c) Recursive definition: \(\(f(n + 1) = f(n)^2 - 2f(n) - 2\)\)
Using the initial condition \(\(f(0) = 3\)\)
\(\[f(1) = f(0)^2 - 2f(0) - 2 = 3^2 - 2 \cdot 3 - 2 = 1\]\)
To find \(\(f(2)\):\)
\(\[f(2) = f(1)^2 - 2f(1) - 2 = 1^2 - 2 \cdot 1 - 2 = -3\]\)
Continuing in the same manner:
\(\[f(3) = f(2)^2 - 2f(2) - 2 = (-3)^2 - 2 \cdot (-3) - 2 = 11\]\)
\(\[f(4) = f(3)^2 - 2f(3) - 2 = 11^2 - 2 \cdot 11 - 2 = 107\]\)
\(\[f(5) = f(4)^2 - 2f(4) - 2 = 107^2 - 2 \cdot 107 - 2 = 11365\]\)
d) Recursive definition: \(\(f(n + 1) = \frac{{3f(n)}}{3}\)\)
Using the initial condition \(\(f(0) = 3\):\)
\(\[f(1) = \frac{{3f(0)}}{3} = \frac{{3 \cdot 3}}{3} = 3\]\)
Since the recursive definition is \(\(f(n + 1) = \frac{{3f(n)}}{3}\)\), the value of \(\(f(n)\)\) remains constant as 3 for all values of \(\(n\)\). Hence, \(\(f(2)\), \(f(3)\), \(f(4)\),\) \(\(f(5)\),\) the value will be 3.
Learn more about recursive definition: https://brainly.com/question/30134998
#SPJ11
Help me! What is the answer to this question!? Provide a step by step explanation please.

Answers
Answer:
x = -5 or x= 2
Step-by-step explanation:
|-4x-6| = 14
There are two solutions, one positive and one negative
-4x-6 = 14 -4x-6 = -14
Add 6 to each side
-4x-6+6 = 14+6 -4x-6+6 = -14+6
-4x = 20 -4x = -8
Divide by -4
-4x/-4 = 20/-4 -4x/-4 = -8/-4
x = -5 x = 2
Now we have to,
find the required value of x.
Given that,
→ |-4x -6| = 14
Let's find the both positive value and negative value,
===================
→ -4x -6 = 14
→ -4x = 14 + 6
→ -4x = 20
→ x = 20/-4
→ [x = -5]
===================
→ -4x -6 = -14
→ -4x = -14 + 6
→ -4x = -8
→ x = -8/-4
→ x = 8/4
→ [x = 2]
===================
Therefore, x is -5 (or) 2 is the answer.
solve the problem. the resistance of a wire varies directly as its length and inversely as the square of its diameter. a 50-ft wire with a 0.4-in. diameter has a resistance of 0.0125ω. find the resistance of a 20-ft wire with a diameter of 0.1-in. round to 4 decimal places if necessary.
Answers
The resistance of a 20-ft wire with a diameter of 0.1-in is 0.08ω
How to determine the resistance of a 20-ft wire with a diameter of 0.1-in?The variation is given as:
Resistance varies directly as its length and inversely as square of diameter
Mathematically, this is represented as
R =kL/D^2
Where k represents the constant of variation.
When L = 50, D = 0.4 in and R = 0.0125, we have
0.0125 =k * 50/0.4^2
This gives
k = 0.4^2 * 0.0125/50
Evaluate
k = 0.00004
Substitute k = 0.00004 in R =kL/D^2
R = 0.00004L/D^2
When L = 20-ft wire and D = 0.1-in, we have:
R = 0.00004 * 20/(0.1)^2
Evaluate
R = 0.08
Hence. the resistance of a 20-ft wire with a diameter of 0.1-in is 0.08ω
Read more about resistance at:
https://brainly.com/question/15313576
#SPJ1
Ed has $64000 invested in stocks paying 6%. How much additional money should he invest in certificates of deposit paying 2% so that the average return on the two investments is 3%
Answers
Ed Moura invests $192000 in certificates of deposit paying 2%.
According to the question,
Ed Moura has $64000 invested in stocks paying 6%.
He invests additional money in certificates of deposit paying 2% =x
so the average return on the two investments is 3%.
64000*6% +2%*x = 3%(64000+x)
Convert percentage to decimal,
⇒64000*0.06 +0.02*x = 0.03(64000+ x)
⇒3840 + 0.02x = 1920 +0 .03x ( using multiply)
⇒3840-1920 = 0.03x - 0.02x
⇒0.03x - 0.02x = 3840 -1920
⇒0.01x = 1920
Both side divide by 0.01,
⇒x = 192000
∴ So, Ed Moura invests $192000 in certificates of deposit paying 2%.
Read more about percentages :
https://brainly.com/question/843074
#SPJ4
HELLPPPP MEEEEE ASAPPPPPPP PLEASEEEEEEEEEEEEWEEEEEEEE

Answers
Answer:SORRY CANT HELP U THERE
Step-by-step explanation:
Which equation demonstrates the distributive property?A) 3 (2 + 8) = 3 (8 + 2)B) 3 (2 + 8) = 3 × 2 + 3 × 8C) (3 × 2) × 8 = 3 × (2 × 8)D) 3 × (2 × 8) = 3 × (8 × 2)
Answers
Evaluate the expression seven (10+4)
Answers
Answer:
\(98\)
Step-by-step explanation:
Given the following question:
\(7(10+4)\)
In order to find the answer, we use PEMDAS and solve.
\(7(10+4)\)
\(10+4=14\)
\(7\times14\)
\(7\times14=98\)
\(=98\)
Hope this helps.
Which is the graph of a quadratic function that has a discriminant value of 0? blue, green, yellow, or purple?
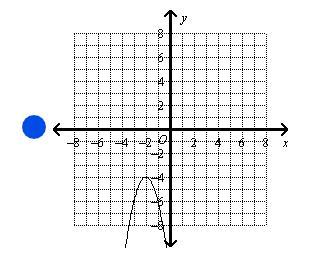
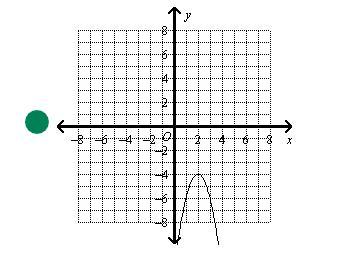
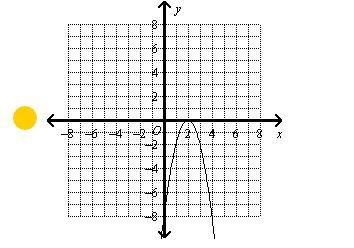

Answers
3/4x + 12 =48 what is the value of ' x '
Answers
Answer:
3/4x + 12 =48
3/4x=36
x=48
Given f(2) = 1093 (92) and g(2) = 30 . Find and simplify (fog) (2)
Refer to image
Given \( f(x)=\log _{3}(9 x) \) and \( g(x)=3^{x} \). Find and simplify \( (f o g)(x) \) \( 2 x \) \( 27^{x} \) \( 2+x \) None of these.
Answers
The simplified expression for (f ∘ g)(x) is 2 + x (option d).
To find and simplify (f ∘ g)(x), we need to substitute the expression for g(x) into f(x) and simplify.
Given:
f(x) = log₃(9x)
g(x) = \(3^x\)
Substituting g(x) into f(x):
(f ∘ g)(x) = f(g(x)) = log₃\((9 * 3^x)\)
Now, we simplify the expression:
log₃\((9 * 3^x)\) = log₃(9) + log₃\((3^x)\)
Since logₓ(a * b) = logₓ(a) + logₓ(b), we have:
log₃(9) + log₃\((3^x)\) = log₃\((3^2)\) + x
Using the property logₓ\((x^a)\) = a * logₓ(x), we get:
log₃\((3^2)\) + x = 2 * log₃(3) + x
Since logₓ\((x^a)\) = a, where x is the base, we have:
2 * log₃(3) + x = 2 + x
Therefore, (f ∘ g)(x) simplifies to:
(f ∘ g)(x) = 2 + x
So, the correct answer is (d) 2 + x.
To know more about expression, refer here:
https://brainly.com/question/31800038
#SPJ4
Complete Question:
Given f(x)=log₃(9x) and g(x)=\(3^x\). Find and simplify (f ∘ g)(x)
(a) 2x
(b) x
(c) \(27^x\)
(d) 2+x
(e) None of these.
