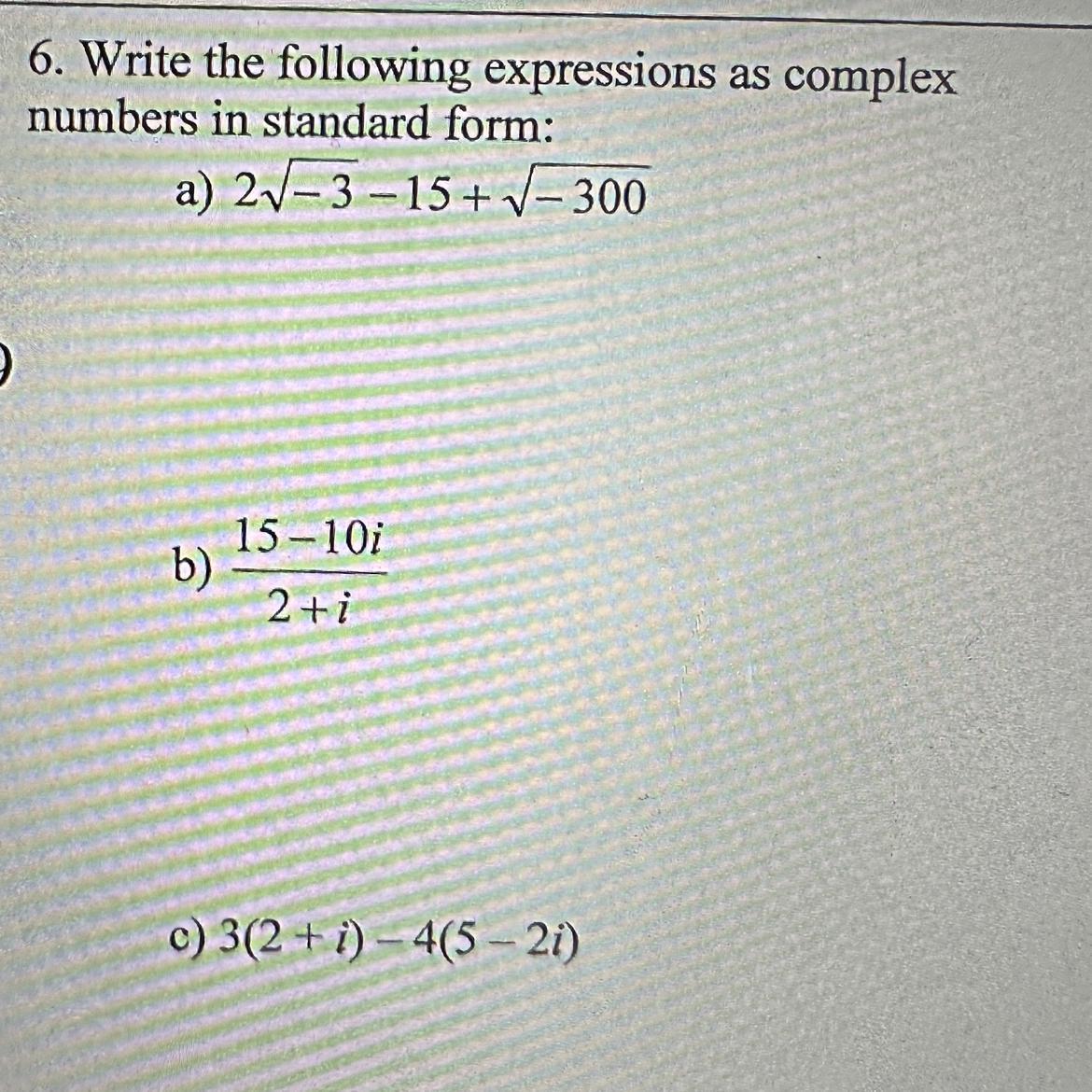Answers
The standard form of the complex number is respectively 2√3 i - 15 + √300 i,4 - 7 i, and -14 + 9 i.
What is a complex number?Complex numbers are helpful in finding the square root of negative numbers.
A complex number is the sum of a real number and an imaginary number.
(a)
As per the given, 2√-3 - 15 + √-300
Since, √-1 = i thus,
2√3 i - 15 + √300 i
(b)
As per the given, (15 - 10i)/(2 + i)
By rationalization,
(15 - 10i)/(2 + i) x (2 - i)/(2 - i)
⇒ (30 - 15 i - 20 i + 10 i²)/(2² - i²)
⇒ (30 - 10 - 35 i)/(4 + 1)
⇒ 4 - 7 i
(c)
As per the given, 3(2 + i) - 4(5 - 2i)
⇒ 6 + 3i - 20 + 8i
⇒ -14 + 9 i
Hence "The complex number has the following conventional forms: 2√3 i - 15 + √300 i,4 - 7 i, and -14 + 9 i".
To learn more about complex numbers,
brainly.com/question/10251853
#SPJ1
Related Questions
Solve the second order differential equation using the method of undetermined coefficients. x" - 25x = t² + t where x'(0) The correct solution will include Yh your "guess" for Yp all your work 1 1 and (0) = 2 Solve the second order differential equation using the method of undetermined coefficients. x" - 25x = 3e²t where a' (0) = 1 and x (0) = 2 The correct solution will include Yh your "guess" for yp all your work.
Answers
For the first differential equation, the solution is: \(\[x(t) = \frac{52}{125}e^{5t} + \frac{78}{125}e^{-5t} -\frac{1}{25}t^2 - \frac{1}{25}t\]\) and for the second second differential equation solution is: \(\[x(t) = \frac{25}{21}e^{5t} + \frac{8}{21}e^{-5t} - \frac{1}{7}e^{2t}\]\)
Equation 1:
\(\[\begin{aligned}x'' - 25x &= t^2 + t, \quad x'(0) = 1, \quad x(0) = 2 \\\end{aligned}\]\)
Step 1: Homogeneous Solution (Yh)
The homogeneous equation is given by:
\(\[x'' - 25x = 0\]\)
The characteristic equation is:
\(\[r^2 - 25 = 0\]\)
Solving for the roots:
\(\[r^2 = 25 \implies r_1 = 5, \quad r_2 = -5\]\)
The homogeneous solution is:
\(\[Yh = c_1e^{5t} + c_2e^{-5t}\]\)
Step 2: Particular Solution (Yp)
Since the right-hand side contains polynomials, we make an educated guess for the particular solution. The form of the particular solution is the same as the right-hand side, but with undetermined coefficients:
\(\[Yp = At^2 + Bt\]\)
Taking derivatives:
\(\[Yp' = 2At + B, \quad Yp'' = 2A\]\)
Substituting these derivatives back into the original differential equation:
\(\[2A - 25(At^2 + Bt) = t^2 + t\]\)
Equating coefficients of like terms:
\(\[-25At^2 = t^2 \implies A = -\frac{1}{25}, \quad -25Bt = t \implies B = -\frac{1}{25}\]\)
The particular solution is:
\(\[Yp = -\frac{1}{25}t^2 - \frac{1}{25}t\]\)
Step 3: Complete Solution
The complete solution is the sum of the homogeneous and particular solutions:
\(\[Y = Yh + Yp = c_1e^{5t} + c_2e^{-5t} -\frac{1}{25}t^2 - \frac{1}{25}t\]\)
Step 4: Applying Initial Conditions
Using the given initial conditions:
\(\[x'(0) = 1 \implies Y'(0) = 1 \implies 5c_1 - 5c_2 - \frac{1}{25} = 1\]\[x(0) = 2 \implies Y(0) = 2 \implies c_1 + c_2 = 2\]\)
Solving these equations, we find:
\(\[c_1 = \frac{52}{125}, \quad c_2 = \frac{78}{125}\]\)
Therefore, the final solution to Equation 1 is:
\(\[x(t) = \frac{52}{125}e^{5t} + \frac{78}{125}e^{-5t} -\frac{1}{25}t^2 - \frac{1}{25}t\]\)
Now, let's move on to the second equation:
Equation 2:
\(\[\begin{aligned}x'' - 25x &= 3e^{2t}, \quad x'(0) = 1, \quad x(0) = 2 \\\end{aligned}\]\)
Step 1: Homogeneous Solution (Yh)
The homogeneous equation is given by:
\(\[x'' - 25x = 0\]\)
The characteristic equation is:
\(\[r^2 - 25 = 0\]\)
Solving for the roots:
\(\[r^2 = 25 \implies r_1 = 5, \quad r_2 = -5\]\)
The homogeneous solution is:
\(\[Yh = c_1e^{5t} + c_2e^{-5t}\]\)
Step 2: Particular Solution (Yp)
Since the right-hand side contains an exponential function, we make an educated guess for the particular solution. The form of the particular solution is the same as the right-hand side, but with undetermined coefficients:
\(\[Yp = Ae^{2t}\]\)
Taking derivatives:
\(\[Yp' = 2Ae^{2t}, \quad Yp'' = 4Ae^{2t}\]\)
Substituting these derivatives back into the original differential equation:
\(\[4Ae^{2t} - 25Ae^{2t} = 3e^{2t}\]\)
Equating coefficients of like terms:
\(\[-21Ae^{2t} = 3e^{2t} \implies A = -\frac{3}{21} = -\frac{1}{7}\]\)
The particular solution is:
\(\[Yp = -\frac{1}{7}e^{2t}\]\)
Step 3: Complete Solution
The complete solution is the sum of the homogeneous and particular solutions:
\(\[Y = Yh + Yp = c_1e^{5t} + c_2e^{-5t} - \frac{1}{7}e^{2t}\]\)
Step 4: Applying Initial Conditions
Using the given initial conditions:
\(\[x'(0) = 1 \implies Y'(0) = 1 \implies 5c_1 - 5c_2 - \frac{2}{7} = 1\]\[x(0) = 2 \implies Y(0) = 2 \implies c_1 + c_2 - \frac{1}{7} = 2\]\)
Solving these equations, we find:
\(\[c_1 = \frac{25}{21}, \quad c_2 = \frac{8}{21}\]\)
Therefore, the final solution to Equation 2 is:
\(\[x(t) = \frac{25}{21}e^{5t} + \frac{8}{21}e^{-5t} - \frac{1}{7}e^{2t}\]\)
To learn more about differential equation, refer to the link;
https://brainly.com/question/28099315
#SPJ4
Pls help
11% of 57 =
39% of 28 =
8% of 97 =
6% of 24.4 =
77% of 9.2 =
Answers
Answer:
1, 6.27, 2, 10.92, 3, 7.76, 4, 1.464, 5, 7.084
Step-by-step explanation:
Answer:
11% of 57= 56.89
39% of 28= 27.61
8% of 97= 96.92
6% of 24.4= 24.34
77% of 9.2= 8.43
Data Island is a beautiful beach resort. It has been a premier touristic destination for over 80 years, and the earliest holiday homes have been built just a few steps away from the beach itself. You work for a real estate agency that sells and rents holiday homes in Data Islands. Recently, one of the interns working on the Data Science Team presents you a report. According to the linear regression model they have run, the price of a house is proportional to its age. But this does not make any sense: after all, newer houses should be worth more.
1. Comment the regression output, noticing that the Sig. column is reporting the p-value of the coefficient. What can you tell about the sign of Age’s slope?
2. Why do you think the model forecasts an higher price for old holiday homes? Think carefully about all the information you have concerning Data Island.
3. Assuming that more data and variables are available, what would you suggest your intern to do to fix their report?
Answers
A lovely beach resort is Data Island. Since it first became a popular tourist destination more than 80 years ago, the earliest vacation homes have been constructed just a few steps from the beach. You are a real estate agent for a company that deals in vacation rentals and sales in the Data Islands. A report was recently presented to you by one of the interns on the data science team. The age of a house affects its price, according to the linear regression model they have ran. But this is absurd because newer homes ought to be more valuable.
1. As the coefficient of Age is positive, so the older the house, the more price it is. Sig. (or p-value) = 0.000 which implies that the co-efficient of Age is significant.
2. This may be that the people who live there are reluctant to sell it, so they quote a higher price or the size of old houses are large or they may be located at prime location.
3. We would ask new interns to consider other independent variables for the regression equation like size of house, location, etc.
To learn more about coefficient click here:
brainly.com/question/27481600
#SPJ4
PLEASE HELP (I’m not good at math )

Answers
Answer:
-5, -3, -1
Step-by-step explanation:
The figure shows a swing blown to one side by a
breeze. As long as the seat of the swing is parallel to
the top bar, the swing makes a parallelogram. In
ABCD, DC = 2 ft, BE 41/2 ft, and m<BAD = 75°

Answers
Answer:
AB=2 ft
ED=4.5 ft
BD=9 ft
m∠ABC=105°
m∠BCD=105°
m∠ADC=75°
Step-by-step explanation:
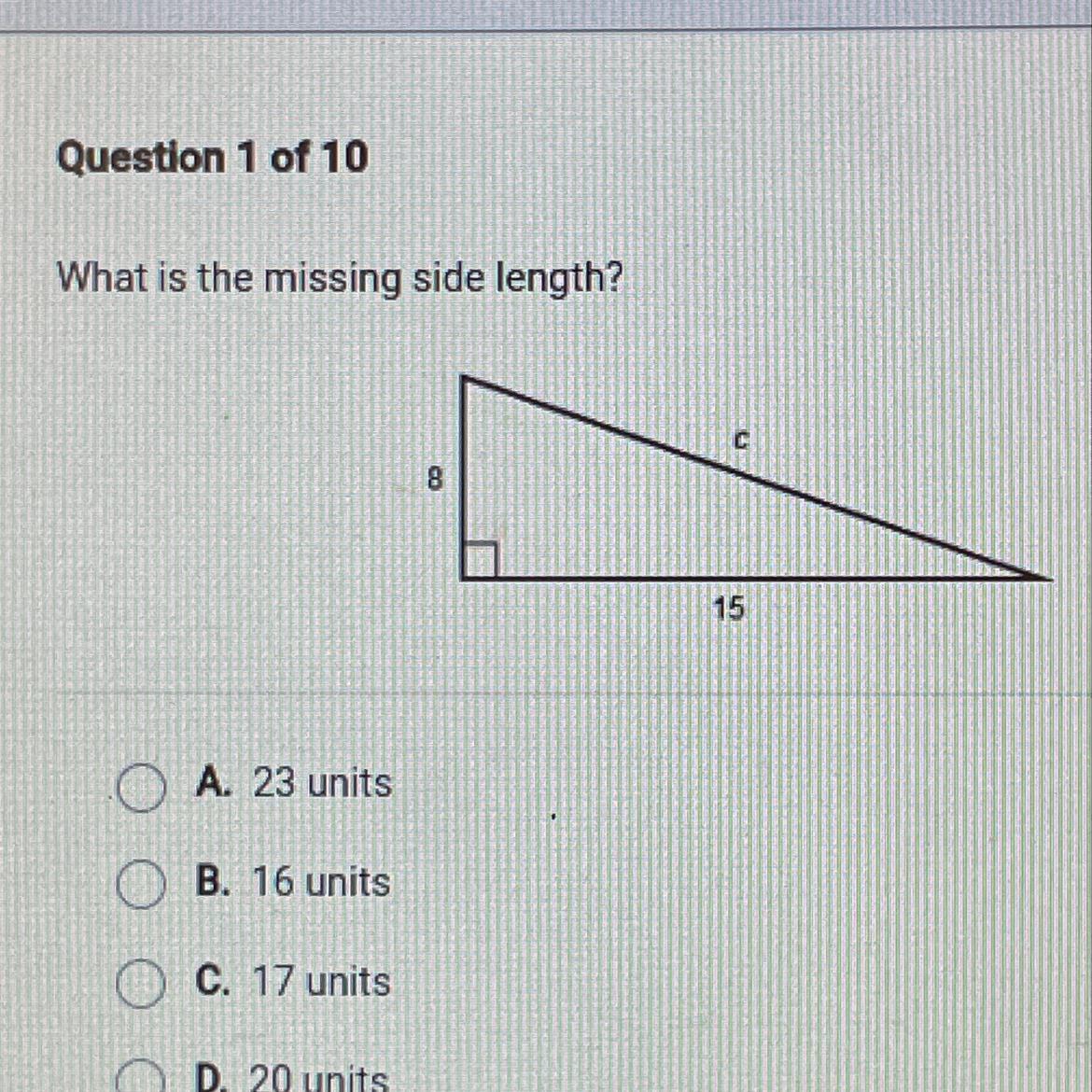
What is the missing side length?
A. 23 units
B. 16 units
C. 17 units
D. 20 units
Answers
Answer:
C. 17 units
Step-by-step explanation:
You want the hypotenuse of a right triangle with legs 8 and 15.
Pythagorean theoremThe Pythagorean theorem tells you the relation between the sides of a right triangle is ...
c² = a² +b² . . . . . . where c is the hypotenuse, and a, b are the legs
Applicationc² = 8² +15² = 64 +225 = 289
c = √289 = 17 . . . . units
The missing side length is 17 units.
__
Additional comment
A set of integers that satisfies the Pythagorean theorem is called a "Pythagorean triple." Perhaps the first one you run across is {3, 4, 5}. Other triples commonly seen are {5, 12, 13}, and {7, 24, 25}. This one, {8, 15, 17} also shows up in algebra and trig problems. It can be worthwhile to remember a few of these.
Their multiples are also seen. For example, {6, 8, 10} is the {3, 4, 5} triple times 2.
The length of a rectangle is 7cm and the width is 4cm. If both the length and the width are increased by equal amounts the area of the rectangle is increased by 42cm find the length and the width of the larger retangle
Answers
The length and width of the larger rectangle are 9cm and 6cm, respectively.
The area of the original rectangle is 7cm x 4cm = 28cm². Let x be the amount by which both the length and the width are increased. Then, the length of the larger rectangle is 7cm + x and the width is 4cm + x. The area of the larger rectangle is (7cm + x)(4cm + x) = 28cm² + 11x + x². Since the area of the larger rectangle is increased by 42cm², we can set up the equation:
(7cm + x)(4cm + x) - 28cm² = 42cm²
Expanding the left-hand side of the equation and simplifying, we get:
11x + x² = 70
Rearranging and solving for x, we get:
x² + 11x - 70 = 0
Factoring the quadratic equation, we get:
(x + 14)(x - 3) = 0
Since the width cannot be negative, the solution is x = 3cm. Therefore, the length of the larger rectangle is 7cm + 3cm = 9cm and the width is 4cm + 3cm = 6cm.
Learn more about rectangle here
https://brainly.com/question/25292087
#SPJ11
Suppose y varies inversely with x, and y = 49 when x = 17
. What is the value of x when y = 7 ?
Answers
Answer:
119 is the value of x when y = 7
Step-by-step explanation:
Since y varies inversely with x, we can use the following equation to model this:
y = k/x, where
k is the constant of proportionality.Step 1: Find k by plugging in values:
Before we can find the value of x when y = k, we'll first need to find k, the constant of proportionality. We can find k by plugging in 49 for y and 17 for x:
Plugging in the values in the inverse variation equation gives us:
49 = k/17
Solve for k by multiplying both sides by 17:
(49 = k / 17) * 17
833 = k
Thus, the constant of proportionality (k) is 833.
Step 2: Find x when y = k by plugging in 7 for y and 833 for k in the inverse variation equation:
Plugging in the values in the inverse variation gives us:
7 = 833/x
Multiplying both sides by x gives us:
(7 = 833/x) * x
7x = 833
Dividing both sides by 7 gives us:
(7x = 833) / 7
x = 119
Thus, 119 is the value of x when y = 7.
Consider the points below. P(θ),−4,0),Q(5,1,−2),R(6,4,1) (a) Find a nonzero vector orthogonal to the plane through the points P,Q, and R. (b) Find the area of the triangle PQR.
Answers
(a) A nonzero vector orthogonal to the plane through the points P, Q, and R is (9, -17, 35). (b) The area of triangle PQR is \(\sqrt\)(811) / 2.
(a) To determine a nonzero vector orthogonal to the plane through the points P, Q, and R, we can first find two vectors in the plane and then take their cross product. Taking vectors PQ and PR, we have:
PQ = Q - P = (5, 1, -2) - (-4, 0, 0) = (9, 1, -2)
PR = R - P = (6, 4, 1) - (-4, 0, 0) = (10, 4, 1)
Taking the cross product of PQ and PR, we have:
n = PQ x PR = (9, 1, -2) x (10, 4, 1)
Evaluating the cross product gives n = (9, -17, 35). Therefore, (9, -17, 35) is a nonzero vector orthogonal to the plane through points P, Q, and R.
(b) To determine the area of triangle PQR, we can use the magnitude of the cross product of vectors PQ and PR divided by 2. The magnitude of the cross product is given by:
|n| = \(\sqrt\)((9)^2 + (-17)^2 + (35)^2)
Evaluating the magnitude gives |n| = \(\sqrt\)(811).
The area of triangle PQR is then:
Area = |n| / 2 = \(\sqrt\)(811) / 2.
To know more about nonzero vector refer here:
https://brainly.com/question/32673773#
#SPJ11
-9.300÷30 ayuda por favor
Answers
Answer:
-9.300÷30
= -310
.................. ;)
HELPP NOWW!! 20 pointssssss

Answers
Answer:
54 square millimeters
Step-by-step explanation:
Answer:
Is a surface area a volume? Because if so its 27. And if its just the flat surface then its 9.
Find five rational number between -3and -2
Answers
Answer:
The five rational numbers between -3 and -2 are : - -13/6, -14/6, -15/6, -16/6, -17/6. so, the rational numbers between -2 & -3 are -13/6, -14/6, -15/6, -16/6, -17/6.
Step-by-step explanation:
if it helped uh please mark me a BRAINLIEST :)
\( \sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}\)
1. Difference: \(\displaystyle\sf (-2) - (-3) = -2 + 3 = 1\).
2. Interval: \(\displaystyle\sf \frac{1}{6}\).
3. Rational Numbers:
a. \(\displaystyle\sf -3 + \text{Interval} = -3 + \left(\frac{1}{6}\right) = -\frac{17}{6}\).
b. \(\displaystyle\sf -3 + 2 \times \text{Interval} = -3 + 2 \times \left(\frac{1}{6}\right) = -\frac{16}{6}\).
c. \(\displaystyle\sf -3 + 3 \times \text{Interval} = -3 + 3 \times \left(\frac{1}{6}\right) = -\frac{15}{6} = -\frac{5}{2}\).
d. \(\displaystyle\sf -3 + 4 \times \text{Interval} = -3 + 4 \times \left(\frac{1}{6}\right) = -\frac{14}{6} = -\frac{7}{3}\).
e. \(\displaystyle\sf -3 + 5 \times \text{Interval} = -3 + 5 \times \left(\frac{1}{6}\right) = -\frac{13}{6}\).
Therefore, the five rational numbers between -3 and -2 are:
\(\displaystyle\sf -\frac{17}{6}, -\frac{16}{6}, -\frac{5}{2}, -\frac{7}{3}, \text{ and } -\frac{13}{6}\).
\(\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}\)
♥️ \(\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}\)
Draw the NFA for the following regular expressions: [6 Marks - 3
Marks each]
i) a*(a+b)* + abc*
ii) a+(c*+d).(bc)*
Answers
The NFAs for a+ and (c*+d).(bc)* by adding appropriate transitions. (q21) becomes the accepting state, representing the completion of the regular expression.
To draw the NFA for the given regular expressions, let's break them down step by step.
i) a*(a+b)* + abc*
NFA for a*
First, let's create the NFA for the subexpression "a*":
┌───┐ a ε
--> │ q0 │─────►(q1)
└───┘
q0 is the initial state, and (q1) is the accepting state. The transition from q0 to (q1) is labeled with "a", and there is also an ε-transition from q0 to (q1). This allows for zero or more occurrences of "a".
NFA for (a+b)*
Next, let's create the NFA for the subexpression "(a+b)*":
a b ε
┌───────┐ ┌─────┐ ┌─────┐
│ │ │ │ │ │
│ q2 ├──► q3 ├──► q4 │
│(start)│ │ │ │ │
└───────┘ └─────┘ └─────┘
│ │ │
│ a │ b │ε
▼ ▼ ▼
┌─────┐ ┌─────┐ ┌─────┐
│ q5 │ │ q6 │ │ q7 │
│(a+b)│ │(a+b)│ │(a+b)│
└─────┘ └─────┘ └─────┘
│ │ │
└─────►(q8) (q9)
accepting
state
q2 is the initial state, q5 and q6 represent the subexpression (a+b). q3 and q4 are intermediary states to allow for looping within the subexpression. The transitions labeled with "a" and "b" connect q2 to q5 and q6, respectively. There are also ε-transitions from q2 to q3 and q6 to q4 to allow for zero or more occurrences of (a+b). Finally, q8 is an accepting state, as it represents the completion of the subexpression (a+b).
NFA for abc*
Now, let's create the NFA for the subexpression "abc*":
┌─────┐ a ε
--> │ q10 │─────►(q11)
└─────┘
│ │
c │ε
│ │
▼ ▼
┌─────┐
│ q12 │
│ c │
└─────┘
q10 is the initial state, and (q11) is the accepting state. There is a transition labeled with "a" from q10 to (q11), and an ε-transition from q10 to q12. From q12, there is a transition labeled with "c", forming a loop back to q12. This allows for zero or more occurrences of "c".
Combining subexpressions
Finally, let's combine the NFAs for the subexpressions a*(a+b)* and abc*:
a ε
┌────
───┐ ┌─────┐ ε
│ │ │ │
│ q0 ├──►(q1) ├──► (q2)
│(start)│ │ │
└───────┘ └─────┘
│ │
│ ε │ε
▼ ▼
┌───────┐ ┌─────┐
│ │ │ │
│ q3 ├──► q4 │
│ │ │ │
└───────┘ └─────┘
│ │
│ ε │ε
▼ ▼
┌─────┐ ┌─────┐
│ q5 │ │ q6 │
│(a+b)│ │(a+b)│
└─────┘ └─────┘
│ │
└─────►(q7)
accepting
state
Here, we have connected the NFAs for a*(a+b)* and abc* by adding ε-transitions. q2 becomes the accepting state, representing the completion of the regular expression.
ii) a+(c*+d).(bc)*
Step 1: NFA for a+
First, let's create the NFA for the subexpression "a+":
┌───┐ a
--> │ q13 │────►(q14)
└───┘
q13 is the initial state, and (q14) is the accepting state. The transition from q13 to (q14) is labeled with "a", allowing for one or more occurrences of "a".
NFA for (c*+d)
Next, let's create the NFA for the subexpression "(c*+d)":
c d
┌───────┐ ┌─────┐
│ │ │ │
│ q15 ├──► q16 │
│(start)│ │ │
└───────┘ └─────┘
│ │
│ c │ d
▼ ▼
┌─────┐ ┌─────┐
│ q17 │ │ q18 │
│ c* │ │ d │
└─────┘ └─────┘
│ │
└─────►(q19)
accepting
state
q15 is the initial state, q17 represents the subexpression c*, and q18 represents the subexpression d. The transitions labeled with "c" and "d" connect q15 to q17 and q15 to q18, respectively. Finally, q19 is an accepting state, representing the completion of the subexpression (c*+d).
NFA for (bc)*
Now, let's create the NFA for the subexpression "(bc)*":
┌─────┐ b ε
--> │ q20 │─────►(q21)
└─────┘ │ │
│ c │ │ε
│ │ ▼ ▼
▼ │
┌─────┐
┌─────┐ │ q22 │
│ q23 │ │ c │
│ b │ └─────┘
└─────┘
q20 is the initial state, and (q21) is the accepting state. There is a transition labeled with "b" from q20 to (q21), and an ε-transition from q20 to q23. From q23, there is a transition labeled with "c" back to q23, forming a loop. This allows for zero or more occurrences of "bc".
Combining subexpressions
Finally, let's combine the NFAs for the subexpressions a+ and (c*+d).(bc)*:
a
┌───────┐
│ │
│ q13 │
│ │
└───────┘
│
│
▼
┌───────┐
│ │
│ q14 │
│ │
└───────┘
│ │
c │ d
│ │
▼ ▼
┌───────┐ b ε
│ │─────►(q21)
│ q15 │ │ │
│(start)│ │ │ε
└───────┘ ▼ ▼
│ ┌─────┐
│ │ q22 │
│ │ c │
│ └─────┘
│
└────►(q19)
accepting
state
Here, we have connected the NFAs for a+ and (c*+d).(bc)* by adding appropriate transitions. (q21) becomes the accepting state, representing the completion of the regular expression.
Learn more about ε-transition here:
https://brainly.com/question/33361458
#SPJ11
Given the table of values for f (x), which of the following
equations represents f-¹ (x)?
CA
X
-2 -3
-1
0
f(x)
2
-1
1 3
5
oft=2
Of¹ (2)=-1
O f¹(a)==
Of¹ (2)=-22-1

Answers
Answer:
(c) f^-1(x) = (x -1)/2
Step-by-step explanation:
The inverse function will give x-values when f(x) values are supplied as arguments. The function can be determined either by using table values to write the function, or by checking the offered functions against the table values.
__
checkingWe want to find f^-1(x) such that f^-1(-3) = -2, matching the first line of the table.
A: (-3 +1)/-2 = 1 ≠ -2B: 1/2(-3) -1 = -5/2 ≠ -2C: (-3 -1)/2 = -2 . . . . . . . . . this function matches the tableD: -2(-3) -1 = 5 ≠ -2The equation representing f^-1(x) is ,..
\(\boxed{f^{-1}(x)=\dfrac{x-1}{2}}\)
__
writingWe can use the first two points in the table to determine the required inverse function:
(x, f^-1(x)) = (-3, -2) and (-1, -1)
The slope is ...
m = (y2 -y1)/(x2 -x1) = (-1 -(-2))/(-1 -(-3)) = 1/2
The y-intercept is ...
b = y1 -m(x1) = -2 -(1/2)(-3) = -1/2
Then the equation of f^-1(x) is ...
y = mx +b
f^-1(x) = 1/2x -1/2 = (x -1)/2
Can y'all help me with this math question

Answers
2*3 and 10power9-10power-8
10 times by the little nuber then times by 6.0
do that for them all
If the monetary multiplier is 6, then the reserve ratio must be:_______
a) 0.06.
b) 0.167.
c) 1.67.
d) 0.6.
Answers
The formula relating the monetary multiplier and the reserve ratio shows that as the monetary multiplier increases, the reserve ratio decreases. If the monetary multiplier is 6, the reserve ratio must be 0.167.
To determine the reserve ratio given the monetary multiplier, we can use the formula:
Monetary Multiplier = 1 / Reserve Ratio
Given that the monetary multiplier is 6, we can substitute this value into the formula:
6 = 1 / Reserve Ratio
To isolate the reserve ratio, we can take the reciprocal of both sides of the equation:
1 / 6 = 1 / (1 / Reserve Ratio)
1 / 6 = Reserve Ratio
Therefore, the reserve ratio must be 1/6 or approximately 0.167.
Among the given options, b) 0.167 represents the correct answer.
Learn more about approximately here:
https://brainly.com/question/31695967
#SPJ11
without using symmetry, determine a definite integral that represents the area of the region enclosed by r = 1 sin θ .
Answers
The definite integral that represents the area of the region enclosed by the polar curve r = 1 sin θ is ∫[a, b] 1/2 r^2 dθ
To determine the definite integral that represents the area of the region, we integrate the expression 1/2 r^2 with respect to θ over the interval [a, b], where a and b are the limits of the region.
In this case, the polar curve r = 1 sin θ represents a circle with radius 1 centered at the origin. As θ varies from 0 to π, the curve traces half of the circle in the positive direction. To find the area of the region enclosed by this curve, we integrate the expression 1/2 r^2 over this interval.
The expression 1/2 r^2 represents the area of a sector of the circle with radius r and central angle θ. Integrating this expression with respect to θ gives us the total area enclosed by the curve.
By evaluating the definite integral over the interval [a, b], we can find the area of the region enclosed by the polar curve r = 1 sin θ.
To know more about area click here
brainly.com/question/13194650
#SPJ11
need 8, and 9 which definitions go with the
description
In a salt where \( r^{+}=165 \) and \( r^{-}=297, r^{+} \)will occupy what kind of hole? tetrahedral octahedral cubic Any of the above 1 point Match each term with the best definition or description
Answers
The salt will acquire octahedral hole. Thus option B is correct .
Given,
\(r^{+} = 165\\ r^{-} = 297\)
Now,
Find the coordination number ,
Radius ratio = \(r^{+} / r^{-}\)
Substitute the values of radius of salt to get the coordination number .
Radius ratio = 165/297
Radius ratio = 0.556 .
If the radius ratio is between 0.414 and 0.732
Range of radius ratio : 0.414 < r < 0.732
Then coordination number is 6 . If the coordination number is 6 then it will acquire octahedral void .
Know more about coordination number,
https://brainly.com/question/31751524
#SPJ4
Mr. Cervantes drove 3,156 miles in December and 8,099 miles in January. Select all the choices that are good estimates for the total number of miles Mr. Cervantes drove for both months by rounding by place values.
A. 11,000 miles
B. 11,100 miles
C. 11,200 miles
D. 11,300 miles
I NEED AN EXPLANATION FOR THIS QUESTION! WHOEVER GIVES ME AN EXPLANATION, I'LL MARK BRAINLIEST!
Answers
if a multiple regression dataset has 3 predictors, what is the minimum number of observations needed to meet doane's rule?
Answers
Doane's rule is used for choosing the number of histogram bins, not for determining the minimum sample size needed for a multiple regression analysis.
However, a commonly cited rule of thumb is that the sample size should be at least 10 times the number of predictors, so for a multiple regression dataset with 3 predictors, a minimum of 30 observations may be recommended.
Doane's rule is a guideline for choosing the number of histogram bins based on the sample size and skewness of the data. It suggests that the number of bins should be approximately equal to 1 + log2(N) + log2(1 + |g1|/SE(g1)), where N is the sample size and g1 is the sample skewness.
It is important to note that Doane's rule is used for determining the number of bins for a histogram, not for determining the minimum sample size needed for a multiple regression analysis.
That being said, in general, the minimum sample size needed for a multiple regression analysis depends on a variety of factors, including the number of predictors, the strength of the relationships between the predictors and the outcome variable, the desired statistical power, and the level of significance. There is no set minimum sample size that applies to all situations. However, a commonly cited rule of thumb is that the sample size should be at least 10 times the number of predictors, so for a multiple regression dataset with 3 predictors, a minimum of 30 observations may be recommended.
Learn more about regression analysis here: brainly.com/question/30011167
#SPJ4
A researcher studied the relationship between the number of times a certain species of cricket will chirp in one minute and the temperature outside. Her data is expressed in the scatter plot and line of best fit below. Based on the line of best fit, what temperature would it most likely be outside if this same species of cricket were measured to chirp 120 times in one minute?

Answers
A certain cylindrical tank holds 20,000 gallons of water which can be drained from the bottom of the tank in 20 minutes the volume tea of water remaining in the tank after T minutes is given by the function (v)= 20,000(1-(t/20)^2 where B is in gallons zero is less than or equal to T which less than or equal to 20 is in a minutes and T equals zero represent the instant the tank starts draining. The average rate of change in volume of water in the tank from time t=0 to t=20 is (v(20)-v(0))/20-0=-1000 gallons/minute. At what time t is the instantaneous rate of the water draining from the tank at 1000 gallons/minute
Answers
Answer:
Impossible. t = 30 minutes.
Step-by-step explanation:
We are given the function.
\(\displaystyle v(t)=20000\left(1-\frac{t}{20}\right)^2, \text{ } 0 \leq t \leq 20\)
Where v(t) represents the amount of gallons remaining after t minutes.
We want to find at what time t is the instanteous rate of change from the tank 1000 gallons per minute.
Hence, find the derivative of the function with respect to time t:
\(\displaystyle \begin{aligned} \frac{d}{dt}[v(t)] &=\frac{d}{dt}\left[20000\left(1-\frac{t}{20}\right)^2\right] \\ \\ v'(t) & = 20000\frac{d}{dt}\left[\left(1-\frac{t}{20}\right)^2\right] \\ \\ & = 20000\left(2\left(1-\frac{t}{20}\right)^1\right)\left(-\frac{1}{20}\right) \\ \\ & = -2000\left(1-\frac{t}{20}\right) \\ \\ & = 100t - 2000\end{aligned}\)
To find the time at which the instanteous rate is 1000 gallons/minute, set v'(t) = 1000 and solve for t:
Hence:
\(\displaystyle \begin{aligned} 1000 &= 100t - 2000 \\ \\ 100t & = 3000 \\ \\ t &= 30\text{ minutes}\end{aligned}\)
Therefore, after 30 minutes, the instantaneous rate of change will be 1000 gallons per minute.
However, v(t) is only defined for 0 ≤ t ≤ 30.
In conclusion, it is impossible for our instantaneous rate of change to ever reach 1000 gallons per minute.
Question 10 (4 points) Find the scalar equation of the plane with vector equation (x,y.-)=(5.1.-1)+s(-4,1.0)+1(1,3,-2)
Answers
The scalar equation of the plane with vector equation (x,y,z)=(5,1,-1)+s(-4,1,0)+t(1,3,-2) is -6x + 2y + 13z = 39.
To find the scalar equation of the plane with vector equation (x,y,z)=(5,1,-1)+s(-4,1,0)+t(1,3,-2), we can use the following steps:
1. Find two vectors in the plane using the given vector equation. We can choose any two linearly independent vectors from the coefficients of s and t:
- Vector v1 = (-4,1,0)
- Vector v2 = (1,3,-2)
2. Find the cross product of the two vectors v1 and v2, which will give us a normal vector to the plane:
- n = v1 x v2 = (-6,2,13)
3. Use the point-normal form of the equation of a plane to write the scalar equation of the plane. We can choose any point on the plane, such as the point (5,1,-1) given in the vector equation:
- The equation of the plane is: -6(x-5) + 2(y-1) + 13(z+1) = 0
- Simplifying the equation, we get: -6x + 2y + 13z = 39
To find the scalar equation of the plane with the given vector equation, we first need to identify the point on the plane and the normal vector to the plane.
The given vector equation is:
(x, y, z) = (5, 1, -1) + s(-4, 1, 0) + t(1, 3, -2)
The point on the plane is the constant vector (5, 1, -1).
Now we need to find the normal vector to the plane. We can do this by taking the cross product of the direction vectors, (-4, 1, 0) and (1, 3, -2):
Normal vector N = (-4, 1, 0) x (1, 3, -2)
N = (1*0 - 3*0, -4*(-2) - 1*0, -4*3 - 1*1)
N = (0, 8, -13)
Now we have the normal vector N = (0, 8, -13) and the point on the plane P = (5, 1, -1). We can find the scalar equation of the plane using the following formula:
A(x - x0) + B(y - y0) + C(z - z0) = 0
where A, B, and C are the components of the normal vector N, and (x0, y0, z0) is the point P on the plane:
0(x - 5) + 8(y - 1) - 13(z - (-1)) = 0
Simplifying, we get the scalar equation of the plane:
8(y - 1) - 13(z + 1) = 0
Visit here to learn more about Vector:
brainly.com/question/25705666
#SPJ11
The probabilities of a positive response for two government programs from the citizens in eight cities are given in the table.
City
Atlanta
Positive Response Positive Response
for Program 1(%) for Program 2 (96)
77. 80
82. 10
86. 40
86. 60
Boston
Chicago
Dallas
65. 90
87. 50
73. 80
80. 90
69. 70
79. 40
78. 40
88. 10
Houston
Los Angeles
Miami
Newark
82. 50
82. 60
81. 40
83. 30
Total
68. 80
81. 70
The chance that a positive response is obtained from Chicago for program 1 is (blank) %. The chance that a positive response is obtained
from Chicago for program 2 is
(Blank) %.
Answers
The number of individuals in Chicago that will respond positively to Program 2 is 22 out of 25.
How to illustrate the information?Probability is the occurence of likely events. It is the area of mathematics that deals with numerical estimates of the likelihood that an event will occur or that a statement is true. An event's probability is a number between 0 and 1.
Given that the chances of a positive response from Chicago residents to two government programs are 65.9% for Program 1 and 87.5% for Program 2, the likelihood of a positive response for Program 2 given that the person is from Los Angeles must be calculated as follows:
87.5 100 = X
43.75 / 50 = X
21.875 / 25 = X
Therefore, 22 out of 25 individuals in Chicago will respond positively to Program 2.
Learn more about probability on:
https://brainly.com/question/24756209
#SPJ1
What is the scale factor of the dilation (with center at the origin) Of point H (6,4) becomes H' (30,20)?
Answers
By using the definition of dilation with center at the origin, the scale factor of the dilation must be equal to 5.
What is the dilation ratio associated with a given point?
Herein we find the coordinates of a point and its image on a Cartesian plane. The latter is the consequence of applying a dilation with center at the origin. Therefore, the following expression defines the transformation:
H'(x, y) = k · H(x, y)
Where:
k - Scale factorH(x, y) - Original pointH'(x, y) - Resulting pointIf we know that H(x, y) = (6, 4) and H'(x, y) = (30, 20), then the scale factor is:
(30, 20) = k · (6, 4)
The expression is true for k = 5.
To learn more on dilations: https://brainly.com/question/13176891
#SPJ1
True or False
(1 point)
2. A function's graph may include solutions that do not appear in its table of values.
O true
false

Answers
Answer:
true
depending on how complete the table of values is.
What is the result of the math formula: =2*10+4^2
Answers
Answer:
36
Step-by-step explanation:
2(10)+4^2
20+4^2
20+16
36
Answer: The result of the math formula =2*10+4^2 is 28.
To calculate this formula, you first need to perform the exponentiation operation of 4^2, which is 16. Then, you multiply 2 by 10, which gives you 20. Finally, you add 20 to 16, which gives you the final answer of 28.
A ferris wheel has a diameter of 224 feet. if a passenger gets in a car and travels 40 feet when the wheel stops to let more passengers on, find the angle of rotation to the nearest tenth of a degree. a 78.2 b 40.9 c 41.2 d 20.5
Answers
Answer:
D) 20.5.
Step-by-step explanation:
To find the angle of rotation, we can use the formula:
Angle of rotation = Arc length / Radius
First, we need to calculate the radius of the ferris wheel. The diameter is given as 224 feet, so the radius is half of that:
Radius = 224 feet / 2 = 112 feet
Now, we can calculate the angle of rotation:
Angle of rotation = 40 feet / 112 feet
Angle of rotation ≈ 0.3571 radians
To convert this to degrees, we multiply by 180/π:
Angle of rotation ≈ 0.3571 * (180/π) ≈ 20.4646 degrees
Rounding to the nearest tenth of a degree, the angle of rotation is approximately 20.5 degrees.
Therefore, the correct answer is option D) 20.5.
82. complete the check register for rob anderson. it has a previous balance of $175.40. He wrote check number 312 for $24.39 on November 22 to the barkber shop. The bank made an automatic transfer (AT) of $65.21 on November 25 to pay is cable bill. He made a deposit of $381.22 on November 27. What is the new balance in rob's account?
Answers
Answer:
$466.62
Step-by-step explanation:
Balance = $175 - $24.39 - $65.21 + $381.22
Use your calculator to add or subtract each new term as indicated:
$175 - $24.39 = $150.61
Next, subtract $65.21: $150.61 - $65.21 = $85.40
Finally, add $381.22: $85.40 + $381.22 = $466.62
on November 27 the new balance in rob's account became $466.62.
Write the equation of the line that passes through (4,2) and has a slope of -2 in
POINT SLOPE FORM. y - y1 = m(x - x1)
Answers
Answer:
y = -2x + 10
Step-by-step explanation:
The equation in point slope form is expressed using the equation
y - y1 = m(x - x1) where;
m is the slope = -2
(x1, y1) is the point on the line = (4,2)
Substitute into the formula:
y - 2 = -2(x - 4)
y -2 = -2x + 8
y = -2x +8 +2
y = -2x + 10
Hence the required equation of the line is y = -2x + 10