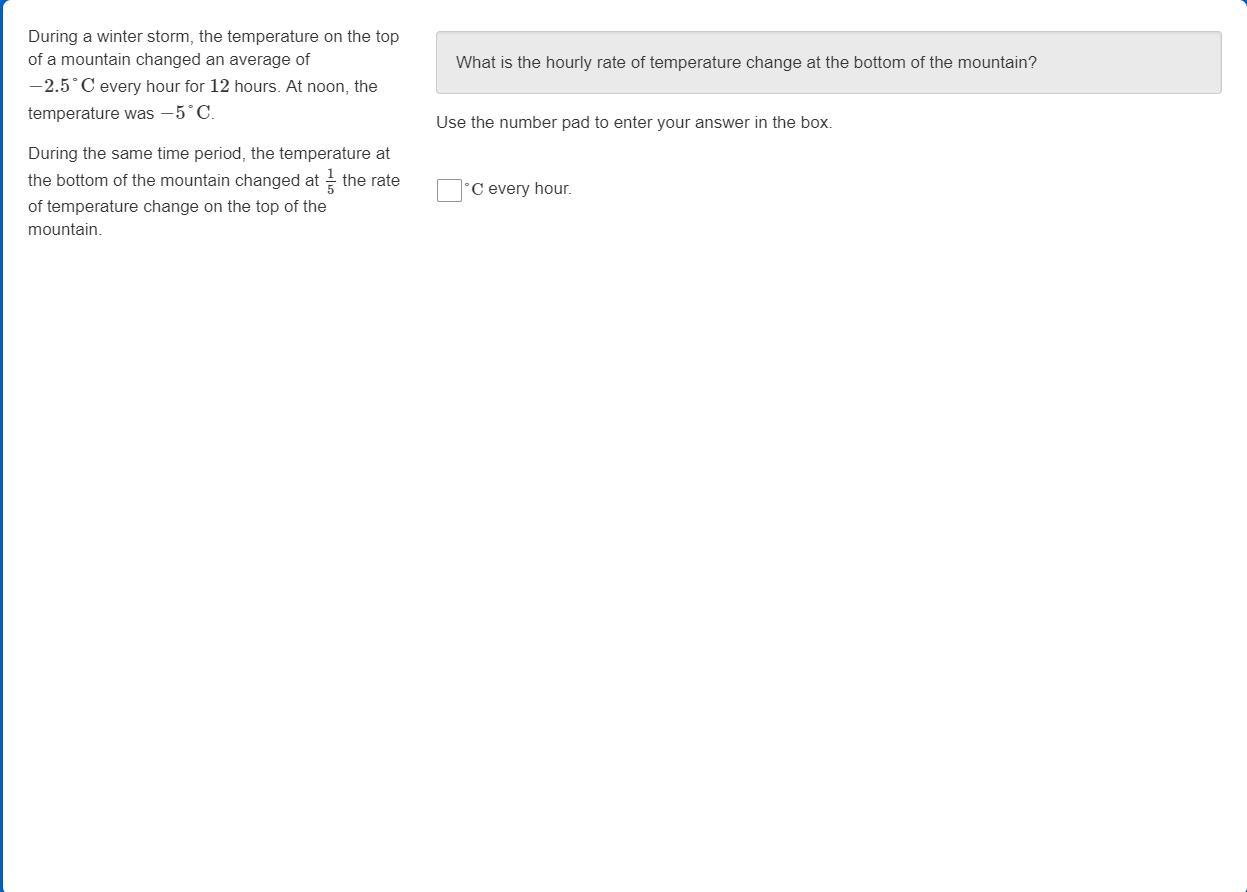
Answers
Answer:
-0.5 degrees Celsius
Step-by-step explanation:
Since the top of the mountain's temp change was -2.5, simple multiply by 1/5 or divide by 5 to get -0.5 and your lower mountain's change of temperature.
Related Questions
paulina and montrose are developing a personality survey and they want to obtain an estimate of its reliability. paulina administers the survey to a group of employees one day and then she administers the exact same survey to the same employees the following week. montrose took a different approach and developed two different, yet equivalent forms of the survey and administered both forms to a sample of employees. paulina is most likely assessing reliability, while montrose is most likely assessing reliability
Answers
Paulina is most likely assessing "Test-retest reliability", while Montrose is most likely assessing "Parallel forms reliability."
What is termed as reliability?The consistency with which a method attempts to measure something is indicated by its reliability. The same method applied to the same sample in the same conditions should yield the same results. If not, the measurement method may be unreliable.
Some key points related to the reliability are-
Test-retest reliability assesses the consistency of the findings when the same test is performed on the same sample at different points in time. When measuring something which you expect to remain constant in your sample, you use it.The correlation among two equivalent versions of the a test is measured by parallel forms reliability. When you have two distinct evaluation tools or sets of questionnaire prepared to measure the same thing, you use it. It is often necessary to develop different versions of tests in educational assessment.To know more about the Test-retest reliability, here
https://brainly.com/question/13860893
#SPJ4
what is the answer? the two triangles below are similar. calculate the value of x

Answers
Step-by-step explanation:
If they are similar, then 10 is to 3 as x is to 15
10/3 = x/15 multiply both sides by 15
50 mm = x
Please solve both with explanation, I’ll give brainliest

Answers
1st and 2nd pictures are for finding area and 3rd picture is for finding perimeter
hope you understood well and if not and you can ask again



Can a right triangle have sides of length 3,4, and 5
Answers
Answer:
yes
Step-by-step explanation:
The equation of a right triangle is the Pythagorean theorum
\(a^2+b^2=c^2\)
Let's say we know 3 and 4:
\(3^2 + 4^2 = c^2\\\\\\9 + 16 = 25\\\\\sqrt{25}=5\)

Which of the following statements is true in its conditional and converse forms?
If K is between points J and L, then K is a midpoint.
If a polygon has 3 sides, then the sum of its interior angles is 180°.
If two angles are right angles, then they are congruent.
If B is the midpoint of AC¯¯¯¯¯¯¯¯, then AB = BC.
Answers
The converse statement involves switching the hypothesis and the conclusion of a conditional statement.
The correct statement is (d) If B is the midpoint of AC, then AB = BC.
The converse of the given conditional statements are:
If K is a midpoint, then K is between points J and LIf the sum of interior angles is 180°, then the polygon has 3 sidesIf two angles are congruent, then they are right anglesIf AB = BC, then B is the midpoint of ACFrom the above statements, (a), (b) and (c) are not the same as the conditional statement, because:
Point K does not have to be between points J and L to be a midpoint.The sum of interior angles of all polygons (whether it has 3 sides or more) is 180 degreesCongruent angles may not be right anglesFor option (d):
For B to be a midpoint of AC, it means that sides AB and BC are congruent.
Hence, the correct statement is (d)
Read more about conditional and converse statements at:
https://brainly.com/question/17684283
rotate point x (0,0)) 270 degrees clockwise about the origin then T<3,5>
Answers
here this probally will help


Answer:
5, 3
Step-by-step explanation:
A town has a population of 17000 and grows at 4% every year. What will be the population after 12 years, to the nearest whole number?
Answers
Step-by-step explanation:
17000 x 1.04 twelve times (.04 is 4% in decimal)
17 000 * 1.04^12 = 27 218
These cones are similar. Find the surface
area of the smaller cone. Round to the
nearest tenth.
2 cm
5 cm
Surface Area = [? ] cm2 Surface Area = 111 cm?

Answers
9514 1404 393
Answer:
17.8 cm²
Step-by-step explanation:
The ratio of surface areas is the square of the ratio of the linear dimensions. The small/large linear dimension ratio is 2/5, so the surface area of the smaller cone is ...
A = (2/5)²(111 cm²) = 17.76 cm²
The area of the smaller cone is about 17.8 cm².
Answer: \(17.8 cm^{2}\)
Please help i dont get this at all so please i will highly appreciate it .Thank youuu!!!

Answers
Answer:
4y^4
Step-by-step explanation:
This polynomial is supposed to be ordered:
-3x^4+4y^4+5x^2y^2-10xy^3+9x^3y
I dont totally understand the question but I hope the ordered polynomial helps
find dy/dx by implicit differentiation. y sin(x2) = x sin(y2)
Answers
The derivative dy/dx of the equation ysin(x^2) = xsin(y^2) is given by (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
In the given equation, y and x are both variables, and y is implicitly defined as a function of x. To find dy/dx, we differentiate each term using the chain rule and product rule as necessary.
Differentiating the left-hand side of the equation, we apply the product rule to ysin(x^2). The derivative of ysin(x^2) with respect to x is dy/dxsin(x^2) + ycos(x^2)*2x.
Differentiating the right-hand side of the equation, we apply the product rule to xsin(y^2). The derivative of xsin(y^2) with respect to x is sin(y^2) + x*cos(y^2)2ydy/dx.
Now we have two expression for the derivative of the left and right sides of the equation. To isolate dy/dx, we can rearrange the terms and solve for it.
Taking the derivative of ysin(x^2) = xsin(y^2) with respect to x using implicit differentiation yields:
dy/dxsin(x^2) + ycos(x^2)2x = sin(y^2) + xcos(y^2)2ydy/dx.
By rearranging the terms, we can solve for dy/dx:
dy/dx * (sin(x^2) - 2yxcos(y^2)) = sin(y^2) - y*cos(x^2)*2x.
Finally, we can obtain the value of dy/dx by dividing both sides by (sin(x^2) - 2yxcos(y^2)):
dy/dx = (sin(y^2) - ycos(x^2)2x) / (sin(x^2) - 2yxcos(y^2)).
Learn more about implicit differentiation here brainly.com/question/31568657
#SPJ11
Solve the question (attached) with full working out and explanation.
Thanks :)
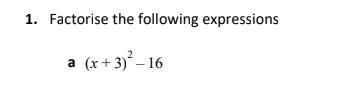
Answers
Step-by-step explanation:
here ya go m8, will this work

write the domained of x using set builder notation y=1410-6y
Answers
Answer:
Step-by-step explanation:
Where properties of y are replaced by the condition that completely describes the elements of the set. The symbol ‘|’ or ‘:’ is used to separate the elements and properties. The symbols ‘|’ or ‘:’ is read as “ such that” and the complete set is read as “ the set of all elements y” such that (properties of y). Here, we are using the variable ‘y’ to formulate the properties of the elements in the set.
Solve the problem.
Find x if m/GTU = -1 + 43x,
m/STG = 70°, and m/STU = 76x + 3.
Pleas help me :)

Answers
Answer:
C) 2
Step-by-step explanation:
Using the angle addition postulate,
\(70-1+43x=76x+3 \\ \\ 69+43x=76x+3 \\ \\ 66=33x \\ \\ x=2\)
A long, thin rod of mass M and length L is standing straight up on a table. Its lower end rotates on a frictionless pivot. A very slight push causes the rod to fall over. As it hits the table, what are
(a) the angular velocity and
(b) the speed of the tip of the rod?
a) Angular velocity is (root) 3g/L
b) Velocity is (root) 3gL
Answers
The angular velocity of tip is 5.42/√L rad/s and the speed of the tip of rod is 5.42√L m/s.
In the given question, a long, thin rod of mass M and length L is standing straight up on a table. Its lower end rotates on a frictionless pivot. A very slight push causes the rod to fall over.
Applying conservation of rotational energy to this situation.
At the start, there is only Potential Energy(PE) and no Kinetic Energy(KE) just before impact, all the PE has converted to KE.
In the starting, the center of mass is half way up, so;
The PE of this system is 1/2 MgL;
where L is the length,
The KE at the end is 1/2 Iw^2
where I is the moment of inertia and w is the angular velocity.
I for a stick pivoted at an end I = 1/3 mL^2, so we have
1/2×m×g×L = 1/2×1/3×m×L^2×w^2
1/2×g = 1/6×lw^2
w = √[3g/L]
A) We have to find the angular velocity.
As we know g=9.8 m/sec^2
w = \(\sqrt{3\times9.8/L}\)
w = √(29.4/L)
w = 5.42√L
The angular velocity of tip is 5.42/√L rad/s.
B) We have to find the speed of the tip of the rod.
The speed of the Tip , v = l×w
v = L × 5.42√L
v = 5.42 × √L
The speed of the tip of rod is 5.42√L m/s.
To learn more about angular velocity link is here
brainly.com/question/29557272
#SPJ4
In ΔOPQ, q = 740 inches, o = 330 inches and ∠P=23°. Find ∠O, to the nearest degree.
Answers
The value of the measure of angle o is 16°
What is a triangle?A triangle is a polygon with 3 sides and 3 angles.
Triangles can be equilateral, isosceles, scalene or right angled depending on the measure of the angles in the triangle.
The sum of the interior angle of an triangle sum up to 180°.
In triangle OPQ, q = 740 inches, o = 330 inches and ∠P = 23°
To find ∠O we need to find p first .
To find p, we use cosine rule,
\(p^{2}\) = \(o^{2}\) + \(q^{2}\) - 2(o)(q)cosP
\(p^{2}\) = \((330)^{2}\) + \((740)^{2}\) -2(330)(740) cos 23
\(p^{2}\) = 108900 + 547600 -488400(0.9205)
\(p^{2}\) = 656500 - 449575
\(p^{2}\) = 206928
p = \(\sqrt{206928}\)
p = 454.889 inches
To find ∠O, we use sine rule, which is,
p/SinP = o/sinO
454.89/sin23 = 330/sinO
By cross multiplying,
454.89sinO = 330sin23
454.89sinO = 330(0.3907)
454.89sinO = 128.7
sinO = 128.7/454.89
sinO = 0.2829
∠O = Arc sin(0.2829)
∠O = 16° to the nearest degree
In conclusion, the measure of ∠O is 16° to the nearest degree
Learn more about cosine rule: https://brainly.com/question/23720007
#SPJ1
which is the total length of both sides of the roof 4x

Answers
Answer:
b. 40m
Step-by-step explanation:
\(length \: of \: x \\ {x}^{2} = {8}^{2} + {6}^{2} \\ {x}^{2} = 64 + 36 \\ {x}^{2} = 100 \\ \sqrt{ {x}^{2} } = \sqrt{100} \\ x = 10m\)
\(x = 10m \\ 4x = 4 \times 10 \\ 4x = 40m\)
Mc Graw Hill < 3-8 Slope and Equations of Lines Question 10 of 12 ✓ Question 10 X = D Find the value of x that satisfies the given conditions. Then graph the line on a separate sheet of paper. The line containing (4, -2) and (x,-6) is perpendicular to the line containing (-2,-9) and (3,-4).
Answers
To solve the problem, we must first find the slope of the line containing (4, -2) and (x, -6). The slope of a line is calculated as the change in y-coordinates divided by the change in x-coordinates, or (y2 - y1) / (x2 - x1). In this case, the slope of the line containing (4, -2) and (x, -6) is (-6 - (-2)) / (x - 4) = -4 / (x - 4)
Since the line containing (4, -2) and (x,-6) is perpendicular to the line containing (-2,-9) and (3,-4), we know that the product of the slopes of these two lines is -1. We can use that information to find the slope of the second line: -1 = (-4 / (x - 4)) * m, where m is the slope of the second line. Solving for m, we get m = -1 / (-4 / (x - 4)) = (x - 4) / 4.
We can now use the point-slope form of a linear equation to find the equation of the line containing (-2,-9) and (3,-4). The point-slope form is y - y1 = m(x - x1). In this case, we can use (-2,-9) as (x1, y1) and (x - 4) / 4 as m:
y - (-9) = (x - 4) / 4 * (x + 2)
Simplifying we get y = (x-4)/4 + (-9) = (x-4)/4 - 9
Now we can substitute x = -2 and y = -9 to check if it belongs to this line:
-9 = (-2 - 4)/4 - 9
-9 = -2/4 - 9
-9 = -0.5 - 9
-9 = -9.5
It match so this line is the correct one.
The value of x that satisfies the given conditions is x = -2
You can graph this line on a separate sheet of paper by plotting the point (-2, -9) and using the slope (x-4)/4 to find additional points on the line.
Select all the ratios that are equivalent to 4:7
8:15
16:28
7:4
20:35
Answers
Answer:
there is no equivalent ratio
Step-by-step explanation:
because 7 is a prime number
16:28
20:35
Explanation:
16:28
= 4 x 4 : 7 x 4
20 : 35
= 4 x 5 : 7 x 5
Which angles are coterminal with 3π2?
Select each correct answer.
Answers
Answer:
Step-by-step explanation: : 630°, 990°, -90°, -450°
Write an equation that represents the line.
Use exact numbers. PLEASE HELP

Answers
Question 16
A line has a slope that is undefined Which of the following points could this line pass through?
А
(6, 4) and (4,-5)
B
(8,5) and (8,-5)
С
(2,3) and (4,3)
D
(-7,1) and (7,6)

Answers
Answer:
b hope it help
Step-by-step explanation:
2)calculate the difference functions for the function below, conclude the difference engine rule: f(n)= 6n2−5n 4
Answers
We can conclude that the difference engine rule for the given function f(n) = 6n^2 - 5n^4 is as follows:
First Difference Function: -20n^3 - 30n^2 - 8n + 1
Second Difference Function: -90n^2 - 122n - 51
To calculate the difference functions for the given function f(n) = 6n^2 - 5n^4, we need to find the differences between consecutive terms. Let's calculate the first few differences:
f(n) : 6n^2 - 5n^4
f(n + 1) : 6(n + 1)^2 - 5(n + 1)^4
Now, let's expand and simplify these expressions:
f(n) : 6n^2 - 5n^4
f(n + 1) : 6(n^2 + 2n + 1) - 5(n^4 + 4n^3 + 6n^2 + 4n + 1)
Expanding further:
f(n + 1) : 6n^2 + 12n + 6 - 5n^4 - 20n^3 - 30n^2 - 20n - 5
Next, we subtract f(n) from f(n + 1) to find the first difference:
f(n + 1) - f(n) : (6n^2 + 12n + 6 - 5n^4 - 20n^3 - 30n^2 - 20n - 5) - (6n^2 - 5n^4)
Simplifying:
f(n + 1) - f(n) : 6n^2 + 12n + 6 - 5n^4 - 20n^3 - 30n^2 - 20n - 5 - 6n^2 + 5n^4
Combining like terms:
f(n + 1) - f(n) : 12n + 6 - 20n^3 - 30n^2 - 20n - 5
Further simplifying:
f(n + 1) - f(n) : -20n^3 - 30n^2 - 8n + 1
Therefore, the first difference function is -20n^3 - 30n^2 - 8n + 1.
To find the second difference function, we need to calculate the differences between consecutive terms of the first difference function:
f(n + 1) - f(n) : -20(n + 1)^3 - 30(n + 1)^2 - 8(n + 1) + 1 - (-20n^3 - 30n^2 - 8n + 1)
Expanding and simplifying:
f(n + 1) - f(n) : -20(n^3 + 3n^2 + 3n + 1) - 30(n^2 + 2n + 1) - 8n - 8 + 20n^3 + 30n^2 + 8n - 1
Combining like terms:
f(n + 1) - f(n) : -20n^3 - 60n^2 - 60n - 20 - 30n^2 - 60n - 30 - 8n + 20n^3 + 30n^2 + 8n - 1
Simplifying further:
f(n + 1) - f(n) : -90n^2 - 122n - 51
Therefore, the second difference function is -90n^2 - 122n - 51.
From the calculations, we can conclude that the difference engine rule for the given function f(n) = 6n^2 - 5n^4 is as follows:
First Difference Function: -20n^3 - 30n^2 - 8n + 1
Second Difference Function: -90n^2 - 122n - 51
The difference engine rule shows how the values of the function change as n increases, and it provides a way to predict future values based on the differences between consecutive terms.
To know more about predict, visit
https://brainly.com/question/27154912
#SPJ11
1. What's the product of 3 2/3 and 14 2/5?
Answers
I don’t know if it’s correct though ♀️
alfred and bonnie play a game in which they take turns tossing a fair coin. the winner of a game is the first person to obtain a head. alfred and bonnie play this game several times with the stipulation that the loser of a game goes first in the next game. suppose that alfred goes first in the first game, and that the probability that he wins the sixth game is m n , where m and n are relatively prime positive integers. what are the last three digits of m n ? (1993,
Answers
So, the last three digits of m*n is 001.
Let p be the probability that Alfred wins given that he goes first. Then, the probability that Bonnie wins given that she goes first is 1-p. Therefore, the probability that Alfred wins the second game given that Bonnie went first in the first game is 1-p. Similarly, the probability that Alfred wins the third game given that he went first in the second game is p, and so on.
Therefore, the probability that Alfred wins the sixth game given that he went first in the first game is:
p(1-p)(1-p)(p)(p)(p) = p^4 (1-p)^2
Since m and n are relatively prime, the last three digits of m*n are the last three digits of p^4 * (1-p)^2, which is the last three digits of p^4 and the last three digits of (1-p)^2. Since p is the probability of winning given that you go first, it is a number between 0 and 1. Therefore, the last three digits of p^4 and (1-p)^2 are 001, resulting in the last three digits of the final answer being 001.
Therefore, the last three digits of m*n is 001.
To learn more about probability
Visit; brainly.com/question/28525447
#SPJ4
pls help Will give u brainliest

Answers
Answer:
give me brainliest first
Step-by-step explanation:
then i shall answer
Suppose that the rate of return on stocks is normally distributed with mean of 9% and a standard deviation of 3%. If I pick five stocks at random, what is the probability that at least two of them will have a return of more than 12%?
Answers
The probability that at least two out of five stocks will have a return of more than 12% is approximately 0.264.
To solve this problem, we can use the binomial distribution. Let X be the number of stocks out of five that have a return of more than 12%.
Then X follows a binomial distribution with n=5 and p=P(return > 12%) where P is the probability function of the normal distribution with mean 9% and standard deviation 3%.
To find P(return > 12%), we can standardize the variable X using the z-score formula:
z = (x - mu) / sigma
where mu = 9% and sigma = 3%. Then,
P(return > 12%) = P(z > (12% - 9%) / 3%) = P(z > 1)
Using a standard normal table or calculator, we find that P(z > 1) = 0.1587.
Now we can calculate the probability of at least two stocks having a return of more than 12%:
P(X >= 2) = 1 - P(X < 2) = 1 - P(X = 0) - P(X = 1)
Using the binomial formula or table, we find that
P(X = 0) = (5 choose 0) * (0.1587)^0 * (1-0.1587)^5 ≈ 0.327
P(X = 1) = (5 choose 1) * (0.1587)^1 * (1-0.1587)^4 ≈ 0.409
Therefore,
P(X >= 2) ≈ 1 - 0.327 - 0.409 ≈ <<0.264>>0.264
To know more about probability refer here:
https://brainly.com/question/30034780#
#SPJ11
solve for y 21+1/10y=30
Answers
The value of y can be determined as,
solve the following proportionx 2— = —32 8x=
Answers
We have to solve for x:
Multiply both sides of the proportion by 32:
\(\frac{x}{32}(32)=\frac{2}{8}(32)\)\(x=\frac{64}{8}\)Simplify:
\(x=8\)Solve this system using ANY method. 3x + 6y = 04x = 2y-10
Answers
To solve this question, let's choose the substitution method. So, you can follow the steps to find x and y.
Step 1: Isolate x in the first equation.
To isolate x:
First, subtract 6y from each side of the equation.
Second, divide both sides by 3.
\(\begin{gathered} 3x+6y=0 \\ 3x+6y-6y=0-6y \\ 3x=-6y \\ \frac{3x}{3}=\frac{-6y}{3} \\ x=-2y \end{gathered}\)Step 2: Substitute x by -2y in the second equation.
\(\begin{gathered} 4x=2y-10 \\ 4\cdot(-2y)=2y-10 \\ -8y=2y-10 \end{gathered}\)Step 3: Isolate y in the equation found in step 2.
To isolate y:
First, subtract 2y from both sides of the equation.
Second, divide both sides by -10.
\(\begin{gathered} -8y=2y-10 \\ -8y-2y=2y-10-2y \\ -10y=-10 \\ \frac{-10y}{-10}=\frac{-10}{-10} \\ y=1 \end{gathered}\)Step 4: Find x by using the relation found in step 1.
Use the equation found in step 1 and substitute y by 1.
\(\begin{gathered} x=-2y \\ x=-2\cdot(1) \\ x=-2 \end{gathered}\)Answer:
x = -2 and y = 1
or
(-2, 1)
Solve the right triangle. 4 3 E F D 60° Write your answers in simplified, rationalized form. Do not round.
Answers
Answer:
\(VW = 6\)
\(WX = 2\sqrt{3}\)
\(\angle V = 30\)
Step-by-step explanation:
Given
\(VX = 4\sqrt{3\)
\(\angle X = 60^\circ\)
See attachment for right triangle
Required
Solve for VW, WX and \(\angle V\)
First, calculate VW
To do this, we make use of:
\(sin(\theta) = \frac{Opposite}{Hypotenuse}\)
In this case,
\(sin(60) = \frac{VW}{4\sqrt{3}}\)
Make VW the subject
\(VW = 4\sqrt{3} * sin(60)\)
In radical form:
\(sin(60) = \frac{\sqrt{3}}{2}\)
\(VW = 4\sqrt{3} * \frac{\sqrt{3}}{2}\)
\(VW = \frac{4\sqrt{3} * \sqrt{3}}{2}\)
\(VW = \frac{4*3}{2}\)
\(VW = \frac{12}{2}\)
\(VW = 6\)
To solve for WX, we make use of Pythagoras Theorem, we make use of:
\(VX^2 = VW^2 + WX^2\)
\((4\sqrt{3})^2 = 6^2 + WX^2\)
\(16*3 = 36 + WX^2\)
\(48= 36 + WX^2\)
Subtract 36 from both sides
\(48 - 36 = 36 - 36 + WX^2\)
\(48 - 36 = WX^2\)
\(12= WX^2\)
Take the square root of both sides
\(\sqrt{12}= WX\)
\(\sqrt{4*3}= WX\)
\(\sqrt{4}*\sqrt{3}= WX\)
\(2\sqrt{3}= WX\)
\(WX = 2\sqrt{3}\)
Solving \(\angle V\)
To do this, we make use of:
\(\angle V + \angle X + 90 = 180\)
Make V the subject
\(\angle V = 180 - 90 - \angle X\)
\(\angle V = 180 - 90 - 60\)
\(\angle V = 30\)