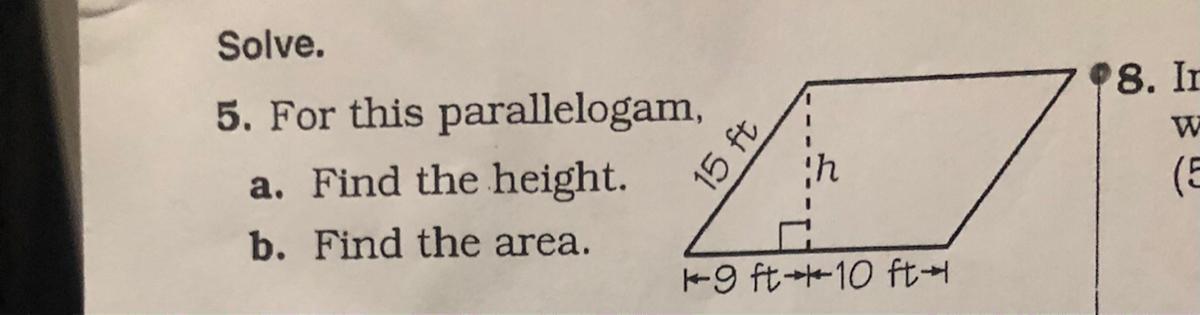Answers
Answer:
a. height = 12
b. area = 228
Step-by-step explanation:
a. To find the height, we can use the triangle formed by the side that measures 15, the side that measures 9. and the height. The hypotenuse of the triangle(the longest side opposite of the right angle), is 15. We can then use the Pythagorean Theorem, which states that \(a^2+b^2=c^2\), where c is the hypotenuse, and a and b are the two other sides. In this case, we need to find a leg of the triangle, not the hypotenuse. What do we do? We can first call the height a, and rearrange the Theorem into \(c^2-b^2=a^2\). \(15^2=225, 9^2=81,\) and \(225-81=\sqrt{144}\)=12. Therefore, the height of the parallelogram is \(\boxed{12}\)
b. To find the area of the parallelogram, we can use the area formula, which is Base*Height. The base is the flat side. We can find the base by adding 9+10=19, and \(19\cdot12=\boxed{228}\)
Related Questions
A student found the MAD of the data shown. What was the student’s error?
A.When calculating the mean, the student divided the sum by the wrong number.
B.When calculating the MAD, the student divided the sum by the wrong number.
C.When calculating the distances to the mean, the student forgot to take the absolute values.
D.When calculating the MAD, the student forgot to take the absolute value of the result.

Answers
The error made while find the mean absolute deviation was: C. When calculating the distances to the mean, the student forgot to take the absolute values.
What is the Mean Absolute Deviation?The mean absolute deviation is simply the average of the sum of the "absolute difference" of the mean and each data point.
In the calculation of the student, after getting the difference of the mean and each data point, the student failed to take the absolute value, and still kept the minus sign included.
Therefore, the error was: C. When calculating the distances to the mean, the student forgot to take the absolute values.
Learn more about the mean absolute deviation on:
https://brainly.com/question/447169
#SPJ1
I roll a fair number cube. What is the probability that it lands on 3?
Answers
The probability that the dice rolled lands 3 is 1/6 respectively.
What is probability?Probability is simply the possibility that something will happen.
When we don't know how something will turn out, we can talk about the possibility of one outcome or the likelihood of several.
The study of events that fit into a probability distribution is known as statistics.
So, find the probability as follows:
Probability formula: P(E) = Favourable events/Total events
Favorable events = 1 which is 3
Total events = 6 which are (1, 2, 3, 4, 5, 6)
Now, insert values as follows:
P(E) = Favourable events/Total events
P(E) = 1/6
Therefore, the probability that the dice rolled lands 3 is 1/6 respectively.
Know more about probability here:
https://brainly.com/question/24756209
#SPJ1
Triangle Congruence by ASA,AAS, and HL Practice
Answers
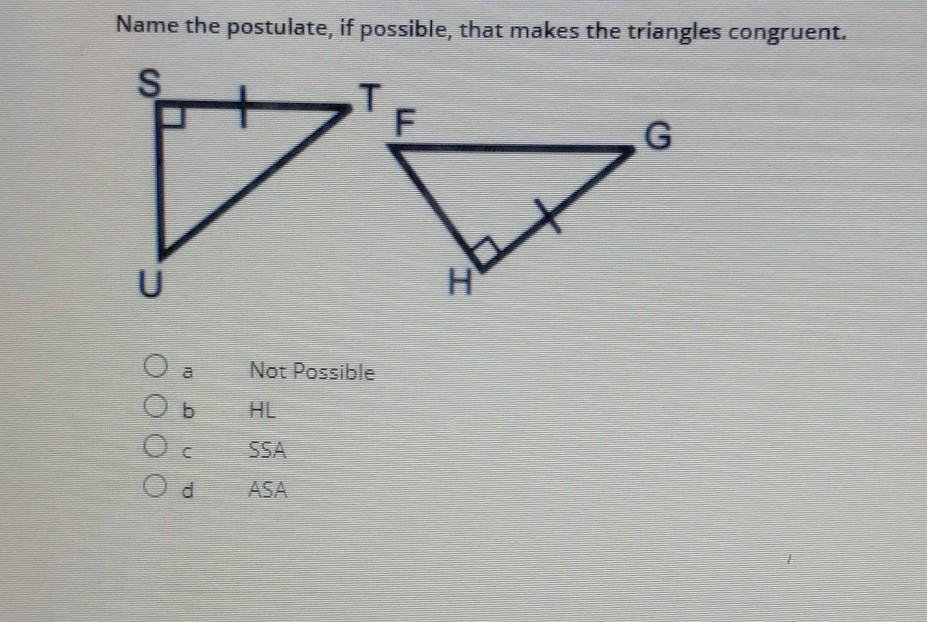
Answer: Not possible.
Step-by-step explanation: It doesn't give you enough information to conclude that they are congruent.
how much time is used to compute f(x) = using a simple routine to perform exponentiation? b. using the routine in section 2.4.4?
Answers
The routine in section 2.4.4 is generally faster and more efficient than the simple routine for computing f(x) = xn, especially for large values of n.
The amount of time used to compute f(x) = xn using a simple routine to perform exponentiation depends on the values of x and n. However, in general, the time complexity of this simple routine is O(n), meaning that the time used to compute f(x) increases linearly with the value of n.
On the other hand, the routine in section 2.4.4 uses a more efficient algorithm to perform exponentiation, with a time complexity of O(log n). This means that the time used to compute f(x) using this routine increases at a much slower rate as the value of n increases.
Know more about routine here:
https://brainly.com/question/30326297
#SPJ11
Say a certain service industry has 78.9 thousand jobs in 2003, but expects to increase at an average annual rate of 2.65 thousand jobs yearly from 2003 to 2013. if this holds true, what will be this industry’s percent increase from 2003 to 2013? a. 28% b. 30% c. 33% d. 40% please select the best answer from the choices provided a b c d
Answers
The correct option is c. 33%.
The job rate of industry’s percent increase from 2003 to 2013 is 33%.
What is percentage increase?The percentage increase would be the change between the final and initial values given as a percentage. We need the initial value and the enhanced (new) value to calculate the percentage.
In other words, % growth is a measurement of percent change that indicates the amount by which a quantity increases in magnitude, strength, or value.
If the % rise is negative, we might conclude that there is corresponding proportion reduction. Let's look at the percentage growth calculation now.
Now, according to the question;
Total Number of years = 10 years
Total number of new jobs created = 2.65 thousand x 10
= 26.5 thousand
= 26,500
Number of jobs in 2013 = 78,900 + 26,500
= 105,400
Percentage increase = (105,400 - 78,900)/78,900 x 100
= 26,500/78,900 x 100
= 0.3359 x 100
= 33.59%
Percentage increase = 33% (approx)
Therefore, the percentage increases in the job between 2003 and 2013 is 33%.
To know more about percentage increase, here
https://brainly.com/question/11360390
#SPJ4
Answer:
C
Step-by-step explanation:
Amira wants to ride her bicycle 48 miles this week. She has already ridden 18 miles. If she rides for 5 more days, write and solve an equation that can be used to determine x, the average number of miles she would have to ride each day to meet her goal.
PLEASE WRITE AN EQUATION
Answers
Answer:
6 miles bicycleriding per day
Step-by-step explanation:
5x+18=48
5x=48-18
5x=30
x=30/5
x=6
Solved X = 6
Step by step
Using y intercept form y=mx + b
Y is the total goal of 48 miles
M is rate, here it is 5 days
X is the unknown miles
B is the y intercept or set amount/starting point, which is the 18 already ridden
So
48 = 5x + 18
Solve
Subtract 18 from both sides to isolate X
48 -18 = 5x +18 - 18
30 = 5x
Divide both sides by 5 to solve for x
30/5 = 5/5 x
6 = x
Now we check our work
48 = 5x + 18
48 = (5) (6) + 18
48 = 30 + 18
48 = 48
Problem solved!
Please help!!!!!!!! I’ve been stuck on this

Answers
Divide by 5 to simplify will give you 1/4
= 0.25 (in decimal form)
Suppose the population mean is equal to 71 and the population variance is equal to 100. Assuming the population is bell-shaped, approximately what percentage of the population values are between 51 and 91?
Answers
As per Chebyshev's theorem, for any data set, at least (1 - 1/k^2) fraction of the data values will lie within k standard deviations of the mean, where k is any positive number greater than 1.
Using Chebyshev's theorem, we can determine the percentage of the population values between 51 and 91 for this question:
k = (91 - 71)/10 = 2
So, at least (1 - 1/2^2) = 75% of the population values will lie between 51 and 91.
However, as the population is assumed to be bell-shaped, we can use the empirical rule to get a more accurate estimate. According to the empirical rule, approximately 68% of the population values will lie within 1 standard deviation of the mean, 95% of the population values will lie within 2 standard deviations of the mean, and 99.7% of the population values will lie within 3 standard deviations of the mean.
The standard deviation of the population is the square root of the variance, which is 10 in this case.
So, we want to find the percentage of the population values that are between 51 and 91, which is 2 standard deviations away from the mean in either direction.
Using the empirical rule, approximately 95% of the population values will lie between (71 - 2(10)) = 51 and (71 + 2(10)) = 91.
Therefore, approximately 95% of the population values are between 51 and 91.
Know more about Chebyshev's theorem here:
https://brainly.com/question/30584845
#SPJ11
A bag contains marbles of four different colors:
• 8 blue marbles
• 24 red marbles
• 16 green marbles
.
4 yellow marbles
The probability of picking a blue marble at random out of the bag is
::
..
2
13
::
8
11
!:
Answers
Answer:
1/6
Step-by-step explanation:
PLEASE MARK AS BRAINLIEST
The probability of getting a blue marble is 0.15.
What is probability?The probability of an event is a number that indicates how likely the event is to occur.
Given that, a bag contains marbles of four different colors: 8 blue marbles, 24 red marbles, 16 green marbles and 4 yellow marbles,
We need to find the probability of picking a blue marble at random out of the bag,
Probability(Event) = Favorable Outcomes / Total Outcomes
Favorable Outcomes = 8
Total Outcomes = 52
Therefore,
P(blue marble) = 8/52 = 0.15
Hence, the probability of getting a blue marble is 0.15.
Learn more about probability, click;
https://brainly.com/question/30034780
#SPJ6
Find the common ratio and write out the first four terms of the geometric sequence {5n34} Common ratio is a1=
a2= a3= a4=
Answers
The first four terms of the geometric sequence ((\(9^n\)) + 2) / 3 with a common ratio of 3 are 1, 11/3, 83/3, and 731/3.
To find the first four terms of the geometric sequence given by the formula ((\(9^n\)) + 2) / 3, where the common ratio is 3, we can substitute different values of n into the formula. Let's calculate each term step by step:
Step 1: Finding a₁ (the first term)
To find the first term (a₁), we substitute n = 0 into the formula:
a₁ = ((\(9^0\)) + 2) / 3
= (1 + 2) / 3
= 3 / 3
= 1
So, a₁ = 1.
Step 2: Finding a₂ (the second term)
To find the second term (a₂), we substitute n = 1 into the formula:
a₂ = ((\(9^1\)) + 2) / 3
= (9 + 2) / 3
= 11 / 3
So, a₂ = 11/3.
Step 3: Finding a₃ (the third term)
To find the third term (a₃), we substitute n = 2 into the formula:
a₃ = ((9²) + 2) / 3
= (81 + 2) / 3
= 83 / 3
So, a₃ = 83/3.
Step 4: Finding a₄ (the fourth term)
To find the fourth term (a₄), we substitute n = 3 into the formula:
a₄ = ((9³) + 2) / 3
= (729 + 2) / 3
= 731 / 3
So, a₄ = 731/3.
Therefore, the first four terms of the geometric sequence ((\(9^n\)) + 2) / 3 with a common ratio of 3 are as follows:
a₁ = 1,
a₂ = 11/3,
a₃ = 83/3,
a₄ = 731/3.
Learn more about geometric sequences at
https://brainly.com/question/27852674
#SPJ4
The question is -
Find the common ratio and write out the first four terms of the geometric sequence {((9^n)+2)/(3)} . The common ratio is 3 .................... a1=? a2= ? a3=? a4=?
A political scientist received a grant to fund a research project on voting trends. The budget includes $3,200 for conducting door-to-door interviews on the day before an election. Undergraduate students, graduate students, and faculty members will be hired to conduct the interviews. Each undergraduate student will conduct 18 interviews for$100. Each graduate student will conduct 25 interviews for $150. Each faculty member will conduct 30 interviews for$200. Due to limited transportation facilities, no more than 20 interviewers can be hired. How many undergraduate students, graduate students, and faculty members should be hired in order to maximize the number of interviews? What is the maximum number of interviews?
Answers
To maximize the number of interviews, 12 undergraduate students, 4 graduate students, and 4 faculty members should be hired. The maximum number of interviews that can be conducted is 684.
Let x, y, and z be the number of undergraduate students, graduate students, and faculty members hired, respectively. The objective is to maximize the number of interviews, which is given by the function
N = 18x + 25y + 30z.
The total cost of hiring interviewers is given by the function
C = 100x + 150y + 200z.
The constraints are x + y + z ≤ 20 (due to transportation limitations), and C ≤ 3200 (the budget constraint). Using linear programming techniques, we can solve for the optimal values of x, y, and z, which are 12, 4, and 4, respectively.
The maximum number of interviews is 18(12) + 25(4) + 30(4) = 684.
Learn more about Simple Maths:
https://brainly.com/question/30198551
#SPJ4
AB is a straight line. XYZ is an isosceles triangle. A What is the value of angle m? A 120° B 95° C 60° D 85° E 75°

Answers
AB is a straight line ⇒ m(∡BXA) = 180°
m(∡BXA) = m(∡BXY) + m(∡YXA) ⇔
⇔ 180° = 60° + m(∡YXA) ⇔
⇔ 60° + m(∡YXA) = 180° ⇔
⇔ m(∡YXA) = 180° - 60° ⇒ m(∡YXA) = 120°
∆XYZ is an isosceles triangle and has an angle of 90° ⇒ m(∡ZXY) = m(∡XYZ) = 45°, because a triangle has 180°
m = m(∡AXZ) ⇒ m(∡AXZ) = ?
m(∡BXA) = m(∡BXY) + m(∡YXZ) + m(∡AXZ) ⇔
⇔ 180° = 60° + 45° + m(∡AXZ) ⇔
⇔ 105° + m(∡AXZ) = 180° ⇔
⇔ m(∡AXZ) = 180° - 105° ⇒ m(∡AXZ) = 75° ⇔
⇔ m = 75°
Good luck! :)
Step by step
An isosceles triangle has two equal angles. Since we know one is 90, the other two sum will be 90 to equal total 180.
90/2 = 45 each angle.
The straight angle AB will sum 180 degrees. We now know one angle is 45, the given angle is 60.
180 - 45 - 60 = 75 degrees. Angle M = 75 degrees.
You have family traveling from far away to come to your house for Thanksgiving. If they travel 342 miles and arrive to your house in 6 hours, how fast were they traveling? * 1 point
Answers
Answer:
they traveled at 57 miles per hour
Answer:
57 mph
Step-by-step explanation:
Brian leaves la at 8. 00am to drive to san francisco 400km away he travels at a steady 50 mph who gets to san drancisco first
Answers
Based on the provided information of speed, A) Beth gets to San Francisco first. B) The first to arrive has to wait for 20 minutes for the second to arrive.
A) To find out who gets to San Francisco first, we need to calculate the time it takes for each of them to travel the distance of 400 miles.
For Brian, we use the formula time = distance / speed:
time = 400 miles / 50 mph = 8 hours
So Brian will arrive in San Francisco at 4:00 p.m. (8:00 a.m. + 8 hours).
For Beth, we use the same formula:
time = 400 miles / 60 mph = 6.67 hours
So Beth will arrive in San Francisco at 3:40 p.m. (9:00 a.m. + 6.67 hours).
Therefore, Beth gets to San Francisco first.
B) To find out how long the first to arrive has to wait for the second, we subtract the arrival time of the first from the arrival time of the second:
wait time = 4:00 p.m. - 3:40 p.m. = 0.33 hours = 20 minutes
So the first to arrive has to wait for 20 minutes for the second to arrive.
Note: The question is incomplete. The complete question probably is: Brian leaves Los Angeles at 8:00 a.m. to drive to San Francisco, 400 miles away. He travels at a steady speed of 50 mph. Beth leaves Los Angeles at 9:00 a.m. and drives at a steady speed of 60 mph. A) Who gets to San Francisco first? B) How long does the first to arrive have to wait for the second?
Learn more about Speed:
https://brainly.com/question/4931057
#SPJ11
A drawer contains black socks and white socks. 70% of the socks are black socks. A
number generator simulates randomly selecting 10 socks from the drawer. The
number generator is used 10 times and the number of black socks in each trial is
shown in the dot plot.
0 1 2 3 4 5 6 7 8 9 10
Which description is correct about the number generator being fair or not?
The number generator is not fair.
The correct percentage of black socks was not
chosen at all.
The number generator is fair. It picked the approximate percentage of black
socks most of the time.
The number generator is not fair. In three experiments, it picked black socks less
than 50% of the time.
The number generator is fair. It only picked black socks half of the time.

Answers
Answer:
Based on the given information, it is not possible to definitively determine whether the number generator is fair or not. However, we can make some observations and inferences:
We know that 70% of the socks in the drawer are black, which means that in a random selection of 10 socks, we would expect to see around 7 black socks on average.
The dot plot shows the number of black socks in 10 trials of the number generator. We can see that the number of black socks varies from 0 to 10, with some frequencies being higher than others.
Without knowing the exact frequencies or probabilities, we can see that the dot plot does not appear to be centered around 7 black socks, which is what we would expect from a fair number generator. However, it is difficult to determine whether the deviations from 7 are statistically significant or not, without more information.
Therefore, based on the given information, the most accurate statement is:
The number generator's fairness cannot be determined with certainty from the given data, but there are indications that it may not be perfectly fair.
Step-by-step explanation:
Jan spends part of her year as a member of a gym. She then finds a better deal at another gym, so she
cancels her membership with the first gym and spends the rest of the year with the second gym. The
membership to the first gym costs $80 per month, while the membership for the second gym costs $45 per
month. If she ends up spending a total of $645 over the course of the year, how much time did she spend at
each gym?
Answers
Answer:
Jan spent $240 at the first gym and $405 at the second gym.
guys help how do i do fings like
63+__=100
I did this 6+_=10 and it’s 4
And 3 + _=0 abs it’s 3 so I thought it was 43 but it’s wrong help
Answers
Answer:
63+37=100 there you go
that the answer
Answer:
37
Step-by-step explanation:
To find out what the missing number is, you can subtract the known number (63) from the sum (100). 100 - 63 = 37.
Find the equation of the line passing through the points (-1,-1) and (3,5).
Answers
Answer:
y = 2/3x + 3
Step-by-step explanation:
(-1,-1) (3,5)
5+1/3+1
6/4
2/3
y = 2/3x + b
5 = (2/3)(3) + b
5 = 2 + b
b = 3
y = 2/3x + 3
If the directrix is a vertical line through the point (4, 0) and the vertex is located at the origin, is the parabola a vertical or horizontal parabola? Which direction does the parabola open?
Answers
Answer:
The parabola is horizontal and opens vertically and in the -y direction.
Step-by-step explanation:
The directrix of a parabola is perpendicular to the axis of symmetry of the curve, in whose direction the parabola opens. If the directrix is vertical, the axis of symmetry is horizontal. Hence, the parabola is horizontal and opens vertically and in the -y direction, since the directrix is represented by \(x = 4\).
A ball is thrown into the air by a baby alien on a planet in the system of Alpha Centauri with a velocity of 31 ft/s. Its height in feet after t seconds is given by y = 31 t − 23 t 2 . A. Find the average velocity for the time period beginning when t=1 and lasting .01 s: .005 s: .002 s: .001 s: NOTE: For the above answers, you may have to enter 6 or 7 significant digits if you are using a calculator. Estimate the instanteneous velocity when t=1.
Answers
The average velocity for the time period is -15 feet per second
The velocity of the ball = 31 feet / seconds
The function of the height is
y = 31t - 23t^2
Time period beginning when t = 1 and lasting .01 s, .005 s, .002 s, .001 s
The average velocity = f(1.01) - f(1) / 1.01 - 1
f(t) = 31t - 23t^2
f(1.01) = 31(1.01) - 23(1.01)^2
= 31.31 - 23.46
= 7.85 feet per second
Similarly
f(1) = 31(1) - 23(1)^2
= 31 - 23
= 8 feet per second
The average velocity = 7.85 - 8 / 1.01 - 1
= -0.15 / 0.01
= -15 feet per second
Hence, the average velocity for the time period is -15 feet per second
Learn more about function here
brainly.com/question/20534410
#SPJ4
what is the density of the rock???!!!!!!!!!!

Answers
Answer:
he actual densities of pure, dry, geologic materials vary from 880 kg/m3 for ice (and almost 0 kg/m3 for air) to over 8000 kg/m3 for some rare minerals. Rocks are generally between 1600 kg/m3 (sediments) and 3500 kg/m3 (gabbro).
Step-by-step explanation:
Use the first derivative and the second derivative test to determine where each function is increasing, decreasing, concave up, and concave down.
y=-3x² -5x+2, XER
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.A. The function is increasing on the interval(s)
(Type your answer in interval notation. Use a comma to separate answers as needed. Type an integer or a simplified fraction.)
B. The function is not increasing on any interval.
Answers
The function is not increasing on any interval.
First, we need to find the first derivative of the function:
y = -3x² - 5x + 2
y' = -6x - 5
Next, we need to find the critical points of the function by setting the first derivative equal to zero:
-6x - 5 = 0
-6x = 5
x = -5/6
Now, we need to use the second derivative test to determine where the function is increasing, decreasing, concave up, and concave down:
y'' = -6
Since the second derivative is a constant negative value, the function is concave down on the entire domain of x.
Now, we can use the first derivative and the critical point to determine where the function is increasing and decreasing:
When x < -5/6, the first derivative is positive, so the function is increasing.
When x > -5/6, the first derivative is negative, so the function is decreasing.
Therefore, the function is not increasing on any interval.
In interval notation, the function is increasing on the interval (-∞, -5/6) and decreasing on the interval (-5/6, ∞).
So, the correct choice is B. The function is not increasing on any interval.
See more about function at; https://brainly.com/question/23819325
#SPJ11
HELP!!!!!!!!!!!!!!!! PLEASE HELP WILL MARK BRAINLIEST!!!!! AND 20 POINTS!

Answers
Answer:
x = 3
Step-by-step explanation:
you need to set them equal to each other since all sides of a square are the same.
5(4x-3) = 5x+30
distribute
20x - 15 = 5x + 30
combine like terms
15x = 45
divide
3
0 = pi/
radians. Identify the terminal point and tan 0
Answers
If 0 = pi/ radians. Then the terminal point is (1, 0), and tanθ = 0.
Given the equation 0 = π / radians.
To find the terminal point we need to use the below formula,θ = 2πn + α
Where,θ = Angle of Terminal Point = Number of revolutions
α = Remaining Angle Thus, here α = 0 radians = 2πn + 0n solving the above equation,
we get,n = 0, 1, 2, ... etc.
As the radian measure is given in the equation, we know that the angle is at the 3 o'clock position on the unit circle, which is also known as the standard position.
So, the terminal point is (1, 0).To find tanθ, we have to use the formula given as tanθ = y / x, where x and y are the coordinates of the terminal point.
Here, x = 1 and y = 0. Hence, tanθ = y / x = 0 / 1 = 0.
Therefore, the terminal point is (1, 0), and tanθ = 0.
Learn more about Radian from the below link
https://brainly.com/question/19278379
#SPJ11
Pleaseee I need helppppp

Answers
Answer:c
Step-by-step explanation:
A group of students volunteered to finish a task in 25 days .1 Q of students did not come n the work could b completed in 35 days .find original number of students in group were??
Answers
Answer:
p=7Q/2
Step-by-step explanation:
Original number of students:
p students to do 1 job in 25 days.
Let r= the rate for 1 student.
pr*25=1
pr*25=1 is the work rate equation for p students.
Lesser number of students:
p-Q students came to do the job and time required was 35 days.
(P-Q)*r*35=1.
The unknowns are p, Q and r
Equate the original number of students and the lesser number of students
pr*25=(P-Q)*r*35
25rp=35rp - 35Qr
Collect like terms
25rp-35rp = -35Qr
Divide both sides by -5
-5rp+7rp=- 7rp
It can be re written as
7rp-5rp=-7Qr
2rp=7Qr
Make p the subject of the formula
p=7Qr/2r
p=7Q/2
p=7Q/2 is the original number of students
-10rp = -35Qr
The system of these two equations can be solved for p. See the THREE unknown
variables, p, r, and Q. You might assume that either r or Q would be a constant.
Increase £89 by 61%
Give your answer rounded to 2 DP.
Answers
Answer:
\( 89 \times \frac{61}{100} = \frac{5429}{100} = 54.29\)
89+54.29=143.29
A movie theater has a seating capacity of 275. The theater charges $5.00 for children, $7.00 for students, and $12.00 of adults. There are half as many adults as there are children. If the total ticket sales was $ 1986, How many children, students, and adults attended? CHILDREN ATTENDED= ? STUDENTS ATTENDED= ? ADULTS ATTENDED=?
Answers
Answer:
Adults = 61
Students = 92
Children = 122
Step-by-step explanation:
a adults
x students
c children
a + c + x = 275
c / a = 2
5c + 7x + 12a = 1986
Simplify and solve the system.
a + 2a + x = 275
3a +x = 275
x = 275 - 3a. and c= 2a
The revenue equation can be written in terms of just one variable, a.
5(2a) + 7(275-3a) + 12a = 1986
Solve for a
a = 61
use it to find x and c.
c = 2a = 2 x 61 = 122
x = 275-a-c
x = 275 - 61-122
x = 92
Help me please
Look at this graph

Answers
Answer:
Slope = Rise/Run
Slope = 1/2
Step-by-step explanation:
Pick two points randomly, it doesn't matter.
Count the rise, then count the run.
Simplify the fraction.
Boom! You got it!
pick a point, for this example i’ll use (20,20)
then calculate how far up and over you need to go to hit another point on the graph:
here we need to go up 1 over 2
so the slope is 1/2
Use the trapezoidal rule to calculate the absolute error of 1∫3(2x^3+10) dx using 4 subintervals. Enter an exact value. Do not enter the answer as a percent.
Answers
To use the trapezoidal rule to estimate the definite integral of the function f(x) = 1/2x^3+10 on the interval [1,3], we need to divide the interval into n subintervals of equal width h, where h = (b-a)/n = (3-1)/4 = 1/2.
Then, we can use the following formula to approximate the definite integral:
∫1^3 (1/2x^3+10) dx ≈ h/2 * [f(a) + 2∑f(xi) + f(b)]
where xi = a + ih for i = 1, 2, ..., n-1.
Applying this formula with n = 4, we get:
∫1^3 (1/2x^3+10) dx ≈ 1/4 * [f(1) + 2f(5/2) + 2f(2) + 2f(7/2) + f(3)]
where f(x) = 1/2x^3+10.
Evaluating f at the endpoints and midpoints of the subintervals, we obtain:
f(1) = 1/2(1)^3+10 = 10.5
f(5/2) = 1/2(5/2)^3+10 = 27.125
f(2) = 1/2(2)^3+10 = 11
f(7/2) = 1/2(7/2)^3+10 = 35.875
f(3) = 1/2(3)^3+10 = 19.5
Plugging these values into the formula, we get:
∫1^3 (1/2x^3+10) dx ≈ 1/4 * [10.5 + 2(27.125) + 2(11) + 2(35.875) + 19.5]
≈ 27.25
To calculate the absolute error, we need to find the exact value of the definite integral:
∫1^3 (1/2x^3+10) dx = [1/8x^4+10x]1^3 = 99/8
The absolute error is then given by:
|∫1^3 (1/2x^3+10) dx - 27.25| = |99/8 - 27.25| = 219/8
Therefore, the exact value of the absolute error is 219/8.
Learn more about trapezoidal, here:
brainly.com/question/22351006
#SPJ11