Answers
Related Questions
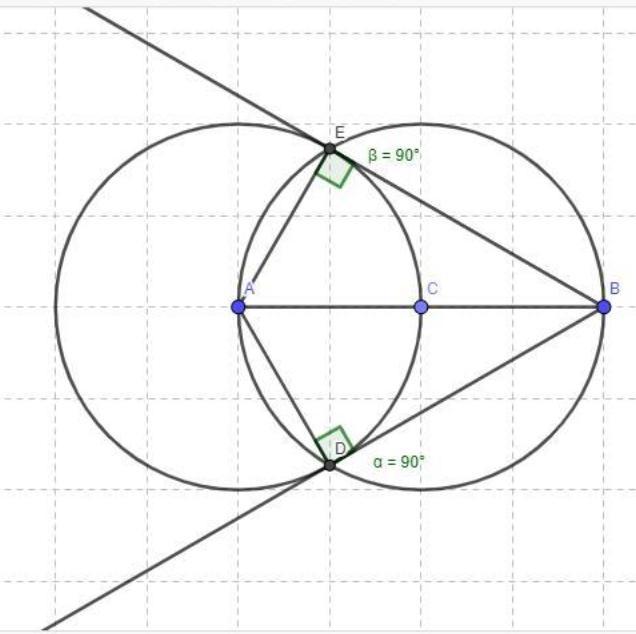
What do the measures of angles BDA and BEA and the fact that and are radii of circle A tell us about and Explain your answer
Answers
The measures of angles BDA and BEA is 90 degree and the fact that AD and AE are radii of circle A tell us about BD and BE must be a tangent to the circle.
The tangents to the circle are BD and BE.
∠BDA = 90
∠BEA = 90
Radii = AD and AE
A tangent's angle with a circle's radius is always measured as a 90-degree angle.
∠BDA = 90, and since AD is a radius, BD must be a tangent to the circle.
Similar, ∠BEA = 90 suggests that BE is a tangent to the circle and that AE is a radius.
To learn more about tangent of circles link is here
brainly.com/question/23265136
#SPJ4
The complete question is:
What do the measures of angles BDA and BEA and the fact that AD and AE are radii of circle A tell us about BD and BE?
2 Use a five-variable Karnaugh map to find the minimized SOP expression for the following logic function: F(A,B,C,D,E) = 2m(4,5,6,7,9,11,13,15,16,18,27,28,31)
Answers
The minimized SOP expression for F(A,B,C,D,E) using a five-variable Karnaugh map is D'E' + BCE'. A five-variable Karnaugh map is a graphical tool used to simplify Boolean expressions.
The map consists of a grid with input variables A, B, C, D, and E as the column and row headings. The cell entries in the map correspond to the output values of the logic function for the respective input combinations.
To find the minimized SOP expression, we start by marking the cells in the Karnaugh map corresponding to the minterms given in the function: 2m(4,5,6,7,9,11,13,15,16,18,27,28,31). These cells are identified by their binary representations.
Next, we look for adjacent marked cells in groups of 1s, 2s, 4s, and 8s. These groups represent terms that can be combined to form a simplified expression. In this case, we find a group of 1s in the map that corresponds to the term D'E' and a group of 2s that corresponds to the term BCE'. Combining these groups, we obtain the expression D'E' + BCE'.
The final step is to check for any remaining cells that are not covered by the combined terms. In this case, there are no remaining cells. Therefore, the minimized SOP expression for the given logic function F(A,B,C,D,E) is D'E' + BCE'.
Learn more about combinations here: https://brainly.com/question/29595163
#SPJ11
In the △ABC, the height AN = 24 in, BN = 18 in, AC = 40 in. Find AB and BC.
btw i need two answers for bc not just one
Answers
Answer:
AB = 30 inch
BC = 14 inch or BC = 50 inch
Step-by-step explanation:
Make a drawing. Please see the attachment. All measurements are in inches.
Consider the two triangles:
∆ ABC and ∆ AB'C
1. Looking only at ∆ ABC. Since this is not a rectangular triangle, let's first consider ∆ ANC, so we can calculate NC.
AN is the height and there fore is perpendicular to NC and thus also to BC.
In ∆ ANC
AN² + NC² = AC²
We want to calculate NC, so:
NC² = AC² - AN²
Given: AC = 40 and AN = 24
NC² = 40² + 24²
NC² = 1600 + 576
NC² = 1024
NC = +-SQRT(1024)
NC = 32
NC = NB + BC
We want to know BC
BC = NC - NB
Given: NB = BN = 18 and we just calculated NC to be 32 so...
BC = 32 - 18
BC = 14
2. Looking only at ∆ AB'C
AN is the height and there fore is perpendicular to B'C. Let's consider ∆ AB'N, so we can calculate AB'.
AN is the height and there fore is perpendicular to B'N, which means it has an angle of 90° in ∆ AB'N.
In ∆ AB'N
c² = a² + b²
AB'² = AN² + B'N²
Given: AN = 24 and B'N = 18
AB'² = 24² + 18²
AB'² = 576 + 324
AB'² = 900
AB' = +-SQRT(900)
AB' = 30
In ∆ AB'C
with AB' = 30 and AC = 40
c² = a² + b²
B'C² = AB'² + AC²
B'C² = 30² + 40²
B'C² = 900 + 1600
B'C² = 2500
B'C = +-SQRT(2500)
B'C = 50
Now we have our answers.
Extra:
Please look at the picture again, but now concentrate on the indicated 50 and - 50...
I am trying to explain something about the meaning of the outcome of mathematical calculations like:
c² = 2500
c = +- SQRT(2500)
c = 50 or c = - 50
Depending on where you want to start from, you can "move" 50 inch in one direction or 50 inch in the opposite direction, hence the -50 inch. Please let me explain why I am making a fuss...
1). Let's consider ∆ AB'C. Going from B' to C, you "move" -50 inch form B' towards C. This 50 inch is what we calculated earlier, but the we neglected to explain why we discarded the minus value of the SQRT... We just stated it to be only the positive value! Normally we give no meaning to the negative variant of it... Well, is this true in this case?
2). Let's consider ∆ ABC'. Going from B to C', you "move" 50 inch form B towards C'. Please understand that the direction is opposite that of - 50 inch in 1).
It is important to understand that a negative sign means the 180° in the direction of the other way.
In general. When calculating a square side by using the SQRT, you carefully need to consider if you can discard the -
minus value of your calculated outcome.
Not always, but usually there is some sort of meaning to the negative part of the SQRT, you just need to be willing to understand what it possibly could mean.
I hope this has made some sense to you :-).

What function is a vertical shift of f(x) = x?
A) g(x) = 3f(x)
B) g(x) = f(x - 3)
C) g(x) = f(x) + 4
D) g(x) = 1/2 f(x)
Answers
Answer:
C) g(x) = f(x) + 4
Step-by-step explanation:
A vertical shift is where you shift, slide or translate the whole graph up or down (on a graph) The way this shows up in the equation is just a number tacked on to the end of the equation. A +anumber (like the +4 in the answer) slides the function UP four units. A
-anumber would slide the function DOWN instead.
As for the other answers:
A) the 3multiplied in front is a vertical STRETCH.
D) the 1/2 multiplied in front is a vertical shrink (smash)
B) The -3 in close tight with the x is a horizontal shift(slide, translate) It is a RIGHT shift. A +anumber would be a LEFT shift. Horizontal shift seem kind of backwards. + goes LEFT and - goes RIGHT.
Find the first six terms of the sequence defined by each of these recurrence relations and initial conditions.
a) an=−2an−1, a0=−1 b) an=an−1−an−2, a0=2, a1=−1
c) an=3a2n−1, a0=1
Answers
The first six terms of the sequence defined by each of these recurrence relations and initial conditions are
a) -1, 2, -4, 8, -16, 32.
b) 2, -1, -3, -2, 1, 3.
c) 1, 3, 9, 27, 81, 243.
a) The first recurrence relation is given by an = -2an-1 with an initial condition of a0 = -1. To find the first six terms of this sequence, we need to use the recurrence relation to generate each term, starting with the initial condition. Using the formula, we can find:
a1 = -2a0 = -2(-1) = 2
a2 = -2a1 = -2(2) = -4
a3 = -2a2 = -2(-4) = 8
a4 = -2a3 = -2(8) = -16
a5 = -2a4 = -2(-16) = 32
a6 = -2a5 = -2(32) = -64
Therefore, the first six terms of the sequence defined by an = -2an-1 with a0 = -1 are: -1, 2, -4, 8, -16, 32.
b) The second recurrence relation is given by an = an-1 - an-2 with initial conditions a0 = 2 and a1 = -1. To find the first six terms of this sequence, we need to use the recurrence relation to generate each term, starting with the initial conditions. Using the formula, we can find:
a2 = a1 - a0 = -1 - 2 = -3
a3 = a2 - a1 = -3 - (-1) = -2
a4 = a3 - a2 = -2 - (-3) = 1
a5 = a4 - a3 = 1 - (-2) = 3
a6 = a5 - a4 = 3 - 1 = 2
Therefore, the first six terms of the sequence defined by an = an-1 - an-2 with a0 = 2 and a1 = -1 are: 2, -1, -3, -2, 1, 3.
c) The third recurrence relation is given by an = 3a2n-1 with an initial condition of a0 = 1. To find the first six terms of this sequence, we need to use the recurrence relation to generate each term, starting with the initial condition. Using the formula, we can find:
a1 = 3a0 = 3(1) = 3
a2 = 3a3 = 3(3) = 9
a3 = 3a2 = 3(9) = 27
a4 = 3a7 = 3(27) = 81
a5 = 3a14 = 3(81) = 243
a6 = 3a29 = 3(243) = 729
Therefore, the first six terms of the sequence defined by an = 3a2n-1 with a0 = 1 are: 1, 3, 9, 27, 81, 243.
To know more about recurrence relations here
https://brainly.com/question/9521757
#SPJ4
Answer the question in photo [ Brainliest + easy points ]
![Answer the question in photo [ Brainliest + easy points ]](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/miEH2hr07APNi8T9BqdxJId1lDaJW8P7.png)
Answers
Answer:
TU = 27
Step-by-step explanation:
ST + TU = SU
(8x - 11) + (14x - 15) = 19x - 17
8x - 11 + 14x - 15 = 19x - 17
22x - 26 = 19x - 17
22x - 19x = 26 - 17
3x = 9
x = 3
TU = 14x - 15 = 14(3) - 15 = 27
Find the value of x in 4000(1.5^x) = 25,000. Show your work.
Answers
Answer:
4.17
Step-by-step explanation:
6000x = 25000
x = 25000 / 6000
x = 4.17
Question in image. :)

Answers
Answer:
All real numbers greater than or equal to 0.
General Formulas and Concepts:
Algebra I
Domain is the set of x-values that can be inputted into function f(x)Step-by-step explanation:
According to the graph, we see that our x-values span from 0 to infinity. Since 0 is a closed dot, it is inclusive in the domain:
[0, ∞) or x ≥ 0 or All Real Numbers greater than or equal to 0.
what is the domain and range of the mapping diagram ?

Answers
Answer:
Below
Step-by-step explanation:
Domain is the 'x' values a function can have for this one {1,3,4,5}
Range is the 'y' values a function has {6,8,10}
a semi circle sits on top of a rectangle. find its area and perimeter . use 3.14 for pi sides 3in by 4 in
Answers
Answer:
Area=14.28 Perimeter= 14.28
Step-by-step explanation:
Area of a circle = (3.14) * r^2
radius = diameter/2
radius = 4/2
r = 2
A = (3.14) * 2^2
A = (3.14) * 4
A = 12.57
since it's a half circle though, 12.57/2 = 6.29
the area of the rectangle is bh, 4*2 = 8
6.29 + 8 = 14.28
area = 14.28
perimeter of a circle, or circumference = 2(3.14)r
C = 2(3.14) * 2
C = 6.28 * 2
C = 12.57
but again, since it's a half circle, 12.57/2 = 6.29
perimeter of a rectangle = 2(l + w)
p = 2(4 + 2)
p = 2(6)
p = 12
but because the perimeter is what's on the outside, we don't count the side connecting to the circle, so it'd be 12 - 4 = 8
6.29 + 8 = 14.28
perimeter = 14.28
Simplify: `\left(4g^{3}h^{4}\right)^{3}`
Answers
The expression \left(\(4g^{3}h^{4}\right)^{3}\)) can be simplified to \(64g^{9}h^{12}.\)
To simplify this expression, we raise each term inside the parentheses to the power of 3. For 4\(g^{3}\), we have \(4^{3}\) = 64 and \((g^{3})^{3}\)= \(g^{9}\), so we get \(64g^{9}\). Similarly, for \(h^{4}\), we have \((h^{4})^{3} = h^{12}\).
Combining these simplified terms, we have \(64g^{9}h^{12}\) as the final simplified form of the expression \left\((4g^{3}h^{4}\)\right)^{3}.
In summary, raising the expression\(4g^{3}h^{4}\) to the power of 3 simplifies to \(64g^{9}h^{12}\).
For more such answers in parentheses
https://brainly.com/question/172432
#SPJ8
Sales tax is currently 9.4 %. Write an algebraic expression to represent the total amount paid for an item that costs D dollars after tax is added to the purchase.
Answers
Answer:
D = p +(.094×p)
Step-by-step explanation:
1. Take 9.4% and make it a decimal. 9.4%=0.094
2. Multiply 0.094 by the original price of the item (seen above as the variable p).
3. Next find the sum of the original price and the number from step 2.
Plugging in some example numbers, we can see this in the expression. Let's leave D as an unknown but make the original price $24. The product of 24 and 0.094 is 2.256. We add this new number to 24 and get 26.256. That's our answer! If the sales tax on a $24 item is 9.4%, the item costs $26.256 after tax is added to the purchase.
Need help ASAP, Tysm i really appreciate it

Answers
Answer:
-5n + 16
Step-by-step explanation:
Distribute the 7 to the equation inside the parenthesis.
7(n + 1) - 12n + 9
7n + 7 - 12n + 9
Bring the -12n towards the 7n.
7n - 12n + 7 + 9
Add or subtract like terms.
7n - 12n + 7 + 9
-5n + 16
Answer:
-5n + 16
A baseball card that was valued at $200 in 1980 has increased in value by 7% each year. Write a function to model this situation, then find the value of the card in 2016
Answers
Answer:
$2284.6
Step-by-step explanation:
Given data
Principal= $200
Rate= 7%
Time= 1980-2016= 36 years
The expression for the exponential model is given as
A= P(b)^t
b=1+r-----------because will are dealing with increase
A= P(1+r)^t
A=200(1+0.07)^36
A= 200(1.07)^36
A= 200*11.423
A=$2284.6
The value of the card is $2284.6
What is the final answer?

Answers
If the maximum value of y=-3x² + mx + 10 is 37, find the values of m.
Answers
Step-by-step explanation:
y = -3x² + mx + 10
dy/dx = -6x + m.
When dy/dx = 0, -6x + m = 0. => x = m/6.
We have y = -3(m/6)² + m(m/6) + 10 = 37.
=> -m²/12 + m²/6 = 27
=> -m² + 2m² = 324
=> m² = 324
=> m = 18 or m = -18.
In the group of 2000 people 40 persent reads science and 30percent reads maths.If 100 people read both then how many people don't read both
Answers
Answer: 500 people don't read both.
Step-by-step explanation:
30% of 2,000 = 600 people read math.40% of 2,000 = 800 people read science.800 + 100 + 600 = 1,500 people either read science, math, or both.2,000 - 1,500 = 500 people don't read math and science.[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][
![[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/qUSYPuIQId66sCaH5yH7cbUdiyAtPtet.png)
Answers
41.25 because you divide the cost into the profit and that equals 41.25
Answer:
$41.25
Step-by-step explanation:
recall that the formula for percent markup is
% Markup = [ (price - cost) / cost ] x 100% (also see attached for reference)
we are given:
% Markup = 65%
Cost = $25
Simply substitute the known values into the formula above
% Markup = [ (price - cost) / cost ] x 100%
65 = [ (price - 25) / 25] x 100
65/100 = (price - 25) / 25
0.65 = (price - 25 ) / 25
0.65 (25) = price - 25
price - 25 = 16.25
price = 25 + 16.25
price = $41.25
![[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][[][][][][][][][][][][][][][][][][[]][][][][][][][][][](https://i5t5.c14.e2-1.dev/h-images-qa/answers/attachments/w1038p0GViMsCJ0vi1a0HhqQvy4BUT4E.jpeg)
PLS ANSER ALL THEM IF U CAN 100 POINT AND BRAINLEST A contractor has made a scale drawing of an addition he will be making to a house. On the drawing each foot is represented by ¾ inch. The length of the room in the drawing is 9 inches and the width is 6 ¾ inches
1.) What is the actual length of the room (in feet)?
2.) What is the actual width of the room (in feet)?
3.) What is the actual perimeter of the room
Answers
Answer:
12 ft for the actual length of the room
9ft for the actual width of the room
42 ft for the actual perimeter of the room
Step-by-step explanation:
Scale is:
1 foot = 3/4 inch
1 inch = 1: 3/4 foot = 4/3 foot
a. The length of the room
9 inches = 9*4/3 foot = 12 ft in the length of the room
b. The width of the room
6 3/4 inches = 27/4 inches = 27/4*4/3 = 9 ft in the width of the room
a. (width+ length) * 2
b. (9+12) *2
42 ft in perimeter of the room
Answer:
12 ft.9 ft.42 ft.Step-by-step explanation:
1.
To find the actual length of the room, we need to convert the length on the drawing from inches to feet. Since each foot is represented by 3/4 inch, we can set up the proportion:
9 inches / (3/4 inch per foot) = x feet
Simplifying the right side of the equation, we get:
9 inches / (3/4 inch per foot) = 12 feet
Therefore, the actual length of the room is 12 feet.
2.
To find the actual width of the room, we need to follow the same process as above. Since the width on the drawing is 6 3/4 inches, we have:
6 3/4 inches / (3/4 inch per foot) = x feet
Simplifying the right side of the equation, we get:
6 3/4 inches / (3/4 inch per foot) = 9 feet
Therefore, the actual width of the room is 9 feet.
3.
To find the actual perimeter of the room, we need to add up the lengths of all four sides. Since the length is 12 feet and the width is 9 feet, we have:
Perimeter = 2(Length) + 2(Width)
Perimeter = 2(12 feet) + 2(9 feet)
Perimeter = 24 feet + 18 feet
Perimeter = 42 feet
Therefore, the actual perimeter of the room is 42 feet.
Matthew had 11.9 meters of string. He cut the string into pieces that were each 0.34 meter long.
How many pieces of string was he able to cut?
Enter your answer in the box.
Answers
Answer:
35
Step-by-step explanation:
11.9/0.34 = 35
Answer: 35
Answer:
35 pieces of string.
Step-by-step explanation:
Matthew was cutting a 11.9 meter piece of string into 0.34 meter pieces, to find the solution for this divide 11.9 by 0.34. If you want to know how to do this by hand I would use a khan academy video.
Aslam and akram invested rs 27000 and rs 30000 to start a business . if they earned a profit of rs 66500 at the end of the year , find the profit of each one
Answers
The profit of Aslam is Rs. 31,474.50 and the profit of Akram is Rs. 35,025.50.
To find the profit of each person, we can use the concept of ratios.
First, let's find the total investment made by both Aslam and Akram:
Total investment = Aslam's investment + Akram's investment
Total investment = 27000 + 30000 = 57000
Next, let's calculate the ratio of Aslam's investment to the total investment:
Aslam's ratio = Aslam's investment / Total investment
Aslam's ratio = 27000 / 57000 = 0.4737
Similarly, let's calculate the ratio of Akram's investment to the total investment:
Akram's ratio = Akram's investment / Total investment
Akram's ratio = 30000 / 57000 = 0.5263
Now, we can find the profit of each person using their respective ratios:
Profit of Aslam = Aslam's ratio * Total profit
Profit of Aslam = 0.4737 * 66500 = 31474.5
Profit of Akram = Akram's ratio * Total profit
Profit of Akram = 0.5263 * 66500 = 35025.5
Therefore, the profit of Aslam is Rs. 31,474.50 and the profit of Akram is Rs. 35,025.50.
To know more about the investment visit:
https://brainly.com/question/29547577
#SPJ11
GIVING BRAINLY
Collect data by conducting a survey that has observations or measurements.
My Topic:
My Question:
My Data Collection Method:
How I Plan to Collect My Data:
How I Plan to Record My Data:
Collect and record your data in this space.
Answers
Topic is Brownies versus cookies
Questions is do people like brownies or cookies more
Data collection method is just asking people
Collection plan is asking family and people in stores
I plan to record this data in a tally mark table
Actual recording in picture

What is the value of log 43? Use the calculator. Round your answer to the nearest tenth. 0. 6 1. 6 3. 8 4. 7.
Answers
Two angles are supplementary. One angle is 155. What is the measure of the other angle?
Answers
Answer: your answer should be an angle that is greater than 90 degrees.
Step-by-step explanation: a supplementary angle is an angle that is greater than 90 degrees. hope it helps :)
A group of 9 workers was assigned to paint the walls in a house, which could be completed in 48 hours. However, after working 8 hours, some of the workers left the group and the remaining workers could complete the job in 72 hours. How many workers left the team? Let x be the number of workers who left the team. (Hint: Focus on the work left after several workers left. )
please show equation with the hint!!
Answers
a group of 9 workers was assigned to paint the walls in a house, which could be completed in 48 hours. Then 1 worker will complete the whole job in 48 × 9 = 432 hours.
worker completes the whole work in 432 hours, then he completed 1/432 of the work per hour.
9 workers complete 9 x 1/432 = 1/48 of work per hour and complete 1/48 x 8 = 1/6 of work in 8 hours.
1 - 1/6 = 5/6 of work left.
this could be completed by n workers in 72 hours so, n/432 x 72 = 5/6
n/6 = 5/6
n = 5
9 - 5 = 4 workers left in the team.
hope this helps!!!!!
(1 1/6 − 7/18 )÷2.8/0.5+ 1/18 =
Answers
You have one box that is 1 4/11
feet tall and a second box that is 1.36 feet tall. Write the decimal expansion for
. If you stack the boxes, about how tall will the stack be?
Answers
The stacked boxes would be 2.72 feet tall
The height of the stacked box is the sum of the lengths of the two boxes
1 4/11 is a mixed number and it has to be converted to a decimal
A mixed number is a number that has a whole number and a proper fraction.
A proper fraction is a fraction is which the numerator is less than the denominator.
The whole number is 1 and the proper fraction is 4/11
To convert to a decimal, divide the numerator by the denominator. Add this number to the whole number
4/11 = 0.36
1 + 0.36 = 1.36 feet
Height of the stacked boxes = 1.36 + 1.36 = 2.72 feet
To learn more about decimals, please check:
https://brainly.com/question/18657762?referrer=searchResults
If mZDEF = (7x + 4)", mZDEG = (5x + 1)', and mZGEF = 23", find each
measure.
E
F
D
Angle DEF -
What is x?
Answers
Answer:
Yoy answer is x=10
Step-by-step explanation:
We already know what ∠GEF is 23°
so you would have to create an equation like this \(23+(5x+1)=7x+4\)
you add 23+1=24 and get \(5x+24=7x+4\) subtract 5x on both sides
\(24=2x+4\) subtract 4 on both sides
\(20=2x\) divide 2 x=10
∠DEF=7(10)=70+4=74
∠DEG=5(10)=50+1=51
To check 51+23=74
what set of ratios is equivalent to 4:5
Answers
By multiplying different natural numbers to the numerator and denominator of the given ratio 4:5, we find out that the set of ratios equivalent to the ratio 4:5 are 8:10 and 12:15.
The given ratio is 4:5.
Let us first rewrite this ratio in the form of fraction. This implies that -
\(4:5=\frac{4}{5}\) -----(1)
We need to find out the set of ratios which is equivalent to 4:5.
In order to find the set of ratios equivalent to 4:5 we need to multiply the numerator and denominator in equation (1) with natural numbers such as 2,3,4, and so on to obtain equivalent fractions of 4/5. These will be the equivalent ratios of 4:5.
Now, firstly multiplying the numerator and denominator of 4/5 with 2 individually, we get
\(\frac{4}{5}\\ =\frac{4*2}{5*2}\\ =\frac{8}{10}\)----(2)
Similarly, multiplying the numerator and denominator of 4/5 with 3 individually, we get
\(\frac{4}{5}\\ =\frac{4*3}{5*3}\\ =\frac{12}{15}\)-----(3)
We can continue to multiply different natural numbers to the numerator and denominator of 4/5 and obtain several set of ratios equivalent to 4:5.
Thus, from equation (2) and (3), we find out that the set of ratios equivalent to 4:5 are 8:10 and 12:15. This is obtained by multiplying natural numbers to the numerator and denominator of the given ratio 4:5.
To learn more about ratios visit
https://brainly.com/question/13419413
#SPJ9
Beth is planning a playground and has decided to place the swings in such a way that they are the same distance from the jungle gym and the monkey bars. if beth places the swings at point d, how could she prove that point d is equidistant from the jungle gym and monkey bars? if segment ad ≅ segment cd, then point d is equidistant from points a and b because congruent parts of congruent triangles are congruent. if segment ad ≅ segment cd, then point d is equidistant from points a and b because a point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects. if m∠acd = 90° then point d is equidistant from points a and b because congruent parts of congruent triangles are congruent. if m∠acd = 90° then point d is equidistant from points a and b because a point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects.
Answers
The angle bisector theorem states that a triangle's opposite side is divided into two halves by an angle bisector that is proportional to the triangle's other two sides.
A point on a perpendicular bisector is equidistant from the endpoints of the segment it intersects, therefore if mACD = 90°, point D is equidistant from points A and B.
Any point on the perpendicular bisector is simply equal distance from both endpoints of the line segment on which it is drawn, according to the perpendicular bisector theorem.
The answer is that point is equidistant from points A and B because a point on a perpendicular bisector is equidistant from the endpoints of the segment it makes up. Therefore, if a pillar is stationed at the middle of a bridge at an angle, all the points on the pillar will be equidistant from the end points of the bridge intersects.
To learn more about Perpendicular bisector theorem refer to:
https://brainly.com/question/4137998
#SPJ4
