Hello,This is super easy!
(i)3x+6-6 = 248
Answers
Answer:
3x+6-6=248
3x=248
x=248/3
x=82.3
Step-by-step explanation:
please mark me as brainlest
Answer:
\(\huge\boxed{\sf x = 82.67}\)
Step-by-step explanation:
Given equation:3x + 6 - 6 = 248
3x = 248
Divide 3 to both sides
x = 248/3
x = 82.67
\(\rule[225]{225}{2}\)
Related Questions
3= g/-4 - 5 solve for g
Answers
Answer:
g= - 27
Step-by-step explanation:
O y=
y = cos(x + 1)
O y = cos(x+ 2x)
y-con~+5 )
Oy= cos(x+8)
©

Answers
Option C - y = cos(x + 5π) is the equation that most closely represents the graph. See attached graph.
What is an equation?In its most basic form, an equation is a mathematical statement that indicates that two mathematical expressions are equal.
The graph of y = cos(x + 5π) is a cosine function that is shifted horizontally 5 units to the left compared to the standard cosine function.
The function is a periodic function that oscillates between -1 and 1, with each cycle shifted 5 units to the left compared to the standard cosine function.
Learn more about equation:
https://brainly.com/question/22688504
#SPJ1

K(x)= -x^2 inverse function SHOW WORK PLEASE HELP FAST
Answers
Steps:
See attachment.
Description:
The first step is to simplify the equation step by step and to simplify an equation you can first multiplying the factors and use the exponent rules to remove the parentheses. After that you need to combine it a terms. Then you will get your answer.
For more steps and graph see the attachment.
Answer: k=−x
Hope this helps.
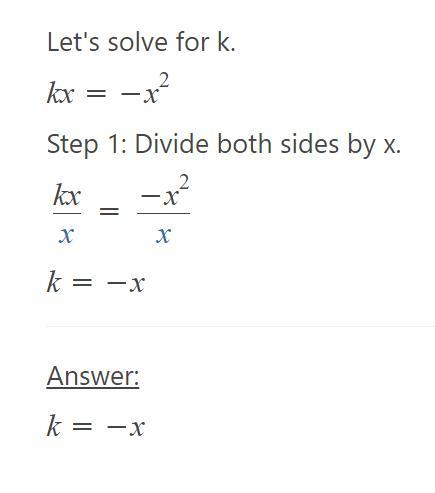
Please help me will give you brainliest!!!

Answers
Polygon ABCD with vertices at A(−4, 6), B(−2, 2), C(4, −2), and D(4, 4) is dilated using a scale factor of three fifths to create polygon A′B′C′D′. If the dilation is centered at the origin, determine the vertices of polygon A′B′C′D′.
A′(5.8, −3), B′(1.6, −1.5), C′(−1.6, 3), D′(2.5, 3)
A′(−12, 18), B′(−6, 6), C′(12, −6), D′(12, 12)
A′(2.4, −3.6), B′(1.2, −1.2), C′(−2.4, 1.26), D′(−2.4, −2.4)
A′(−2.4, 3.6), B′(−1.2, 1.2), C′(2.4, −1.2), D′(2.4, 2.4)
Answers
If the dilation is centered at the origin, determine the vertices of polygon A′B′C′D′ are: D. A′(−2.4, 3.6), B′(−1.2, 1.2), C′(2.4, −1.2), D′(2.4, 2.4).
What is dilation?In Geometry, dilation can be defined as a type of transformation which typically changes the size of a geometric object, but not its shape. This ultimately implies that, the size of the geometric object would be increased or decreased based on the scale factor used.
Next, we would have to dilate the coordinates of the preimage by using a scale factor of 3/5 centered at the origin as follows:
Ordered pair A (-4, 6) → Ordered pair A' (-4 × 3/5, 6 × 3/5) = Ordered pair A' (-2.4, 3.6).
Ordered pair B (-2, 2) → Ordered pair B' (-2 × 3/5, 2 × 3/5) = Ordered pair B' (-1.2, 1.2).
Ordered pair C (4, -2) → Ordered pair C' (4 × 3/5, -2 × 3/5) = Ordered pair C' (2.4, -1.2).
Ordered pair D (4, 4) → Ordered pair D' (4 × 3/5, 4 × 3/5) = Ordered pair D' (2.4, 2.4).
Read more on dilation here: https://brainly.com/question/11812796
#SPJ1
need help with couple more help

Answers
Explanation:
The word "plane" is a parallelogram. If we re-read the question replacing plane with parallelogram, the question is:
Which line INTERSECTS the parallelogram?There is only one line that is intersecting the whole parallelogram. Line J is intersecting the parallelogram because it is the only line that is not being covered in the parallelogram.
Final Answer:
Line JThe figure shows three tennis balls in a can with each tennis ball having a diameter of 2.5 inches. What is the total volume of the air space around the three tennis balls?
Answers
The total volume of the air space of spherical ball is A = 12.265625 inches³
Given data ,
Since each tennis ball has a diameter of 2.5 inches, the radius of each ball is 1.25 inches.
The air space around the balls can be thought of as a cylinder with a height equal to the diameter of one ball and a radius equal to the radius of one ball.
The height of the cylinder is 2.5 inches, and the radius is 1.25 inches.
The formula for the volume of a cylinder is:
V = πr²h
V = ( 3.14 ) ( 1.25 )² ( 7.5 )
V = 36.796875 inches³
where V is the volume, r is the radius, and h is the height.
So, the volume of the one ball is:
V₁ = ( 4/3 )π(1.25)³
V₁ = 8.177083 inches³
The total volume of three balls is = volume of 3 spherical balls
V₂ = 3V₁ = 3(8.177083) ≈ 24.53125 cubic inches
Therefore, the total volume of the air space around the three tennis balls is approximately A = 36.796875 inches³ - 24.53125 inches³
A = 12.265625 inches³
Hence , the volume of air space is A = 12.265625 inches³
To learn more about sphere click :
https://brainly.com/question/27933834
#SPJ1
Can you find the surface area and volume pls? ITS WORTH 50 points

Answers
Answer:
Solution given:
r=4in
h=4in
surface area=2πr(r+h)=2π*4(4+4)=64π or201.06ft²
Volume=πr²h=π*4²*4=64π or 201.06ft³
What is the postulate or theorem allows you to state that triangle DEF ~ Triangle GHJ

Answers
Answer:
AAA postulate
Step-by-step explanation:
because similar triangle only have the axiom of angle not side...i mean i guesss if im wrong sorry but still thanks for the points
Answer:
sas
Step-by-step explanation:
the answer is just sas i took the assignment
QUESTION IN IMAGE, WILL GIVE BRAINLIEST AND LOTS OF POINTS

Answers
Answer:
Option 1
Step-by-step explanation:
(3)(-17.25) = -51.75, he withdrew $51.75.
3 because he withdrew a total of 3 times.
-17.25 because he was taking out money.
Answer:(3)(-17.25)= -51.75
Step-by-step explanation:
What is 75.4 in expanded form
Answers
Answer: 75.4 =
70
+ 5
+ 0.4
Step-by-step explanation:
Hope this helps :)
Solve for x. And determine the angle measure of angle FED. Assume line whichappears tangent is tangent.7x - 10EF120°X =
Answers
since the angle is on the circumference, therefore:
solve for x:
\(undefined\)Enter a positive value for d that makes this statement true: 18 *d less than 18 but greater than 0
Answers
Answer:
d=0.5
Step-by-step explanation:
18 x 0.5=9
9 is less than 18 and greater than 0
Answer:
9
Step-by-step explanation:
|x+2|+4=11
A) x=5,-9
Answers
Answer:
the mod always gives positive answers
so the answer will be
Step-by-step explanation:
x+2+4=11
x+6=11
x=11-6
x=5
answer is x is 5
Answer:
x=5,9
Step-by-step explanation:
|x+2|+4=11
|x+2| = 7
next you get two answers by adding two or subtracting two. SO the right answer should be 5 and 9. A is wrong . I DONT SEE THE OTHER ANSWER CHOICES BUT THIS IS WHAT I GOT.
why is -14 smaller than 14
Answers
Answer:
because it's in the minus area and is not a whole number.
Consider a medium with parameters € = 1.2 (10^-10 )F/m , n= 3(10^-3) H/m and sigma=0. Magnetic field intensity in the medium is given as R = 2cos (10^10t- 600x)äz Am.
Use Maxwell's equations to obtain the followings:
1) Magnetic flux density
These questions is circuit theory
Answers
Using Maxwell's equations, we can determine the magnetic flux density. One of the Maxwell's equations is:
\(\displaystyle \nabla \times \mathbf{H} = \mathbf{J} + \frac{\partial \mathbf{D}}{\partial t}\),
where \(\displaystyle \nabla \times \mathbf{H}\) is the curl of the magnetic field intensity \(\displaystyle \mathbf{H}\), \(\displaystyle \mathbf{J}\) is the current density, and \(\displaystyle \frac{\partial \mathbf{D}}{\partial t}\) is the time derivative of the electric displacement \(\displaystyle \mathbf{D}\).
In this problem, there is no current density (\(\displaystyle \mathbf{J} =0\)) and no time-varying electric displacement (\(\displaystyle \frac{\partial \mathbf{D}}{\partial t} =0\)). Therefore, the equation simplifies to:
\(\displaystyle \nabla \times \mathbf{H} =0\).
Taking the curl of the given magnetic field intensity \(\displaystyle \mathbf{R} =2\cos( 10^{10} t-600x)\hat{a}_{z}\, \text{Am}\):
\(\displaystyle \nabla \times \mathbf{R} =\nabla \times ( 2\cos( 10^{10} t-600x)\hat{a}_{z}) \, \text{Am}\).
Using the curl identity and applying the chain rule, we can expand the expression:
\(\displaystyle \nabla \times \mathbf{R} =\left( \frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial y} -\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial z}\right) \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Since the magnetic field intensity \(\displaystyle \mathbf{R}\) is not dependent on \(\displaystyle y\) or \(\displaystyle z\), the partial derivatives with respect to \(\displaystyle y\) and \(\displaystyle z\) are zero. Therefore, the expression further simplifies to:
\(\displaystyle \nabla \times \mathbf{R} =-\frac{\partial ( 2\cos( 10^{10} t-600x)) \hat{a}_{z}}{\partial x} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Differentiating the cosine function with respect to \(\displaystyle x\):
\(\displaystyle \nabla \times \mathbf{R} =-2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z\).
Setting this expression equal to zero according to \(\displaystyle \nabla \times \mathbf{H} =0\):
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x)\hat{a}_{z} \mathrm{d} x\mathrm{d} y\mathrm{d} z =0\).
Since the equation should hold for any arbitrary values of \(\displaystyle \mathrm{d} x\), \(\displaystyle \mathrm{d} y\), and \(\displaystyle \mathrm{d} z\), we can equate the coefficient of each term to zero:
\(\displaystyle -2( 10^{10}) \sin( 10^{10} t-600x) =0\).
Simplifying the equation:
\(\displaystyle \sin( 10^{10} t-600x) =0\).
The sine function is equal to zero at certain values of \(\displaystyle ( 10^{10} t-600x) \):
\(\displaystyle 10^{10} t-600x =n\pi\),
where \(\displaystyle n\) is an integer. Rearranging the equation:
\(\displaystyle x =\frac{ 10^{10} t-n\pi }{600}\).
The equation provides a relationship between \(\displaystyle x\) and \(\displaystyle t\), indicating that the magnetic field intensity is constant along lines of constant \(\displaystyle x\) and \(\displaystyle t\). Therefore, the magnetic field intensity is uniform in the given medium.
Since the magnetic flux density \(\displaystyle B\) is related to the magnetic field intensity \(\displaystyle H\) through the equation \(\displaystyle B =\mu H\), where \(\displaystyle \mu\) is the permeability of the medium, we can conclude that the magnetic flux density is also uniform in the medium.
Thus, the correct expression for the magnetic flux density in the given medium is:
\(\displaystyle B =6\cos( 10^{10} t-600x)\hat{a}_{z}\).
what percent of 41 is 27.9 round the answer to the nearest hundredth of a percent if necessary
Answers
Answer:
11.43
If this helps, make sure to rate it 5 stars and give me brainliest and a thanks!
The number 27.9 is 68.05 percent of 41.
We have,
To find what percent 27.9 is of 41, we can use the following formula:
Percentage = (27.9 / 41) * 100
Calculating this expression:
Percentage = (27.9 / 41) * 100 ≈ 68.0487
Rounded to the nearest hundredth of a percent, the answer is approximately 68.05%.
Thus,
The number 27.9 is 68.05 percent of 41.
Learn more about percentages here:
https://brainly.com/question/11403063
#SPJ6
Please answer ASAP I will brainlist

Answers
Answer:
x = - 2 , x = 4
Step-by-step explanation:
the x- intercepts are the points on the x- axis where the graph crosses
the graph crosses the x - axis at - 2 and 4 , then
x- intercepts are x = - 2 , x = 4
Juan sold a bicycle at a discount of 15%. If the selling price was $340, find the usual price of the bicycle.
Answers
Answer: $400
Step-by-step explanation:
Discount = 15%
The original price/value of an item is always 100%
So selling price (%) = original price - discount = 100%-15% = 85%
We got selling price as 85%
This implies that 85% = 340
Let's find 1% first, then 100%
1% = 340÷85 = 4
100% = 4 × 100 = $400
The usual (normal/original) price is $400
Juan sold a bicycle at a discount of 15% if the selling price was $340 then the usual price of the bicycle was $400.
What is Percentage?percentage, a relative value indicating hundredth parts of any quantity.
Let's represent the usual price of the bicycle by P.
Since Juan sold the bicycle at a discount of 15%, the selling price (S) would be 85% of the usual price (P).
We can express this relationship as an equation:
S = 0.85P
We also know that the selling price of the bicycle was $340.
Substituting S = $340 into the equation above, we get:
$340 = 0.85P
To find P, we can solve for it:
P = $340 / 0.85
P = $400
Therefore, the usual price of the bicycle was $400.
To learn more on Percentage click:
https://brainly.com/question/24159063
#SPJ2
How to solve 2 and 1/2 divided by 3?
Answers
Answer: 5/6
Step-by-step explanation:
2 and 1/2 = 2.5
2.5 / 3 = 5/6 = 0.8333333
don't u have a calculator?
One number exceeds another by 5.The sum of their squares is 157. What are the numbers?
Answers
We have two numbers that we will call x and y.
One number exceeds the other by 5, so we can express it as an equation like:
\(y=x+5\)where y exceeds x by 5.
The sum of the squares is 157, so we can express this as:
\(x^2+y^2=157\)We can replace y with the first expression and obtain:
\(\begin{gathered} x^2+(x+5)^2=157 \\ x^2+x^2+10x+25=157 \\ 2x^2+10x+25-157=0 \\ 2x^2+10x-132=0 \\ x^2+5x-66=0 \end{gathered}\)We now have a quadratic equation.
We can solve it as:
\(\begin{gathered} x=\frac{-5\pm\sqrt{5^2-4(1)(-66)}}{2(1)} \\ x=\frac{-5\pm\sqrt{25+264}}{2} \\ x=\frac{-5\pm\sqrt{289}}{2} \\ x=\frac{-5\pm17}{2} \\ \Rightarrow x_1=\frac{-5-17}{2}=\frac{-22}{2}=-11 \\ \Rightarrow x_2=\frac{-5+17}{2}=\frac{12}{2}=6 \end{gathered}\)We have two possible solutions: -11 and 6.
We can check both:
1) If x = -11, then y is -6, and the sum of the squares is 121 + 36 = 157, so it is valid.
2) If x = 6, then y is 11 and the sum of the squares will also be 157, so it is also a valid solution.
Answer:
If both numbers are positive, they are 6 and 11.
If negative numbers are allowed, the pair of numbers -11 and -6 is a valid solution too.
A body of 60000g is moved through a distance of 8m. Calculate the work done. [take g=10m/s^2]
Answers
Answer:
8m=10m
Step-by-step explanation:
A circle has a diameter of 24 in what is the circumference pi is 3.14
Answers
Answer:
The circumference of a circle is calculated using the formula: C = πd, where C represents the circumference and d represents the diameter of the circle.
In this case, the diameter of the circle is given as 24 inches.
Using the formula, we can substitute the values:
C = πd
C = 3.14 * 24
C ≈ 75.36 inches
Therefore, the circumference of a circle with a diameter of 24 inches (and using π = 3.14) is approximately 75.36 inches.
Step-by-step explanation:
a thief uses a bag of sand to replace a gold statue that sits on a weight-sensitive, alarmed pedestal. the bag of sand and the statue have exactly the same volume, 1.90 ll. (assume that the mass of the bag is negligible.) part a calculate the mass of each object. (densityofgold
Answers
4.65 kg the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
Given that,
A gold statue that is perched on a pedestal with a weight-sensitive alarm is replaced by a thief using a bag of sand. The statue and the bag of sand have the exact same volume, 1.55 L.
We have to calculate the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
We know that,
Mass of gold = Volume × Density
= 1.55×1000 cc × 19.3
= 29915 grams
= 29.915 Kg
Mass of sand = 1.55×1000×3
= 4650g
= 4.65 Kg
Volume = 1.55 L
= 1.55 × 1000 cc
= 1550 cc
Mass = Volume × Density
Mass of gold = 1550 × 19.3
= 29915 grams
= 29.915 kg
Mass of sand = 1550 × 3
= 4650 grams
= 4.65 kg
Therefore, 4.65 kg the mass of each item (assuming the bag's mass is negligible). (Sand density is 3.00 g/cm3, while the density of gold is 19.3 g/cm3)
To learn more about mass visit: https://brainly.com/question/16940422
#SPJ4
10 Kofi scored 45% in the first paper of his mathematics examination and scored x% in the second paper (where x is a whole number). He was given a grade C for the subject, which meant that the average of his marks on the two papers was greater than 48% but less than 52%. Find the possible values of x. [WAEC]
Answers
The possible values of x are 51% < x < 59%.
When you are given various values, the range of those values is how big the difference is between the largest value and the smallest value. In other words, the range is what you get when you subtract the smallest value in the group from the largest value in the group.
Its possible values are 1, 2, 3, 4, 5, and 6; each of these possible values has a probability of 1/6. 4. The word “random” in the term “random variable” does not necessarily imply that the outcome is completely random in the sense that all values are equally likely.
Let K represent Kofi
1st paper = 45/100
2nd paper = x / 100
Mean score = ( 45 + x ) % / 2
The possible range of x = 48% < (45+X)/2 < 52%
Cross multiplying
96% < 45 + x < 104%
Subtract 45 from both sides
Range = 51% < x < 59%
Learn more about probability here https://brainly.com/question/24756209
#SPJ9
Solve the equation for x: -5x + 10 = -40
a x=6
b x=-6
c x=10
d x=-10
e x=-18
f x=18
Answers
For each ordered pair (x, y), determine whether it is a solution to the inequality y≤0.
(8,-43)
(4.-22)
(-3,25)
(-7,45)
Is it a solution?
Answers
Answer:
(8,-43)
(4,-22)
Step-by-step explanation:
In order for the ordered pair to be a solution of the inequality, you must be able to plug in the y-value of the ordered pair and it must be less than or equal to 0.
For example:
(4,-22)
x=4 ; y=-22
Plug y into the inequality
y≤0
-22≤0
Since the statement is true, I know that (4,-22) must be a solution to the inequality.
Another way to solve this problem is by graphing. If an ordered pair is in the shaded region, it is a solution to the inequality. Attached is a graph of both the inequality and ordered pairs plotted.
If this answer helped you, please leave a thanks or a Brainliest!!!
Have a GREAT day!!!

Answer:
Step-by-step explanation:
To determine whether each ordered pair is a solution to the inequality y ≤ 0, we need to check if the y-coordinate of each pair is less than or equal to zero.
Let's check each ordered pair:
(8, -43):
The y-coordinate is -43. Since -43 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(4, -22):
The y-coordinate is -22. Since -22 is less than zero, this ordered pair is a solution to the inequality y ≤ 0.
(-3, 25):
The y-coordinate is 25. Since 25 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
(-7, 45):
The y-coordinate is 45. Since 45 is greater than zero, this ordered pair is not a solution to the inequality y ≤ 0.
So, the solutions to the inequality y ≤ 0 are:
(8, -43) and (4, -22).
5x100+4x10+6x1+2 x 1 10th + 8 x 1 1000th
Answers
Step-by-step explanation:
500+40+6+220+88000=
88766
A cookie factory uses 1 1/3 bags of flour in each batch of cookies. The factory used 6 2/3 bags of flour yesterday. How many batches of cookies did the factory make
Answers
Answer: you can get the full fraction by multiplying 6x3 which is 18 so then you add 18 and 2 and you get 20 so now the fraction is 20/3
and you need 11/3 for a batch so now you have 1 whole batch and 9/3 so you just make the 11 a percentage which is 81%
so the answer is 1 whole batch and 81% of another
or 1 9/3
43% adults favor the use of unmanned drones by police agencies. Twelve U.S. adults are randomly selected. Find the probability that the number of U.S. adults who favor theuse of unmanned drones by police agencies is (a) exactly three, (b) at least four, (c) less than eight(a) P(3) =(Round to three decimal places as needed.)
Answers
EXPLANATION:
According to the established pattern that only 43 out of 100 adults favor the use of drones, now we must find out from the only twelve adults surveyed how much corresponds to 43 percent.
The first thing we must do is make the relation 12 equals 100, then 43 percent how much?
\(\begin{gathered} 12\rightarrow100 \\ x\leftarrow43 \\ x=\frac{12\times43}{100} \\ \textcolor{#FF7968}{x=5.16}\text{\textcolor{#FF7968}{ ; }} \\ \text{the answer is }\text{\textcolor{#FF7968}{5.16 }}\textcolor{#FF7968}{that}\text{\textcolor{#FF7968}{ is less than eight }}\text{; } \end{gathered}\)