hello I'm wondering you are able to help me with this math question on my homework thank you

Answers
Given:
Each yearly payment = P = $680
The rate of the interest = r = 5.6% = 0.056
Compunded annually, n = 1
Time = t = 17 years
We will find the value at the end of the time using the following formula:
\(A=P*\frac{((1+\frac{r}{n})^{nt}-1)}{\frac{r}{n}}\)substitute with the given values:
\(\begin{gathered} A=680*\frac{((1+0.056)^{17}-1)}{0.056} \\ \\ A\approx18,519.63819 \end{gathered}\)Rounding to the nearest cent
So, the answer will be:
A = 18519.64
Related Questions
Jane took 10 min to drive her boat upstream to water-ski at her favorite spot. Coming back later in the day at the same boat speed took her 5 min. If the current in that part of the river is 10 km per hr, what was her boat speed in still water?
Answers
Answer: B = 15 kph or 15 kph
step by step
(b-5)*10=(b+5)*5
10b-50=5b+25
5b=75
b=15 kph in still water
fv=100000, pmt=4000, i/y=5%, n=10, what is pv?
Answers
The Present value is $6,139.132.
We have,
FV=100000, pmt = 4000, I =5%, n=10
So, The present value formula is
PV=FV / (1 + \(i)^n\)
So, PV = 100, 000 / (1+ 5/100\()^{10\\\)
PV = 100,000 / (1+ 0.05\()^{10\\\)
PV = 100, 000/ (1.05\()^{10\\\)
PV = 100,000 / 1.6288946
PV= $6,139.132
Learn more about Future Value here:
https://brainly.com/question/14860893
#SPJ1
8th Grade Which expression is equivalent to 1/27
Answers
Answer:
\(( \frac{1}{3})^{3} \)
Step-by-step explanation:
There are many expressions that can be equivalent to 1/27.
For example, 2/54, 3/81 etc
But I think the expression you are looking for is
\( \frac{1}{27} = \frac{1 \times 1 \times 1}{3 \times 3 \times 3} = \frac{ {1}^{3} }{ {3}^{3} } = ( \frac{1}{3} )^{3} \)
Hope this is helpful
Divide the following complex numbers:
(4-i)/(3+4i)
A.-8/7 + 19/7i
B. 16/25 - 19/25i
C. 8/25 - 19/25i
D. -16/7 + 19/7i
Answers
Answer:
C. 8/25 - 19/25i
Step-by-step explanation:
Given that:
\(\dfrac{4-i}{3+4i}\)
\(= \dfrac{(4-i) (3-4i)}{(3+4i)(3-4i)}\)
\(= \dfrac{(4-i) (3-4i)}{(3+4i)(3-4i)} \\ \\ =\dfrac{12 -16i -3i+4i^2}{9 - 12i +12i -16i^2} \\ \\ = \dfrac{12-19i+4i^2}{9-16i^2} \\ \\ = \dfrac{8-19i}{25}\)
\(=\dfrac{8}{25}- \dfrac{19i}{25}\)
What is the standard form equation with roots at -2, 1, & 8 and goes through the point (0,48)
Answers
The standard form of the equation with roots at -2, 1, & 8 and goes through the point (0,48) is y = x³ - 7x² - 10x + 64.
What is the Cubic equation?Cubic equations are polynomials of degree 3. That means the maximum degree of the polynomial is three.
And the standard form of the cubic equation is;
f(x) = ax³ + bx² +cx +d, where a, b, c, and d are constant coefficients a ≠ 0.
Given:
The roots of the equation are -2, 1, & 8.
So, the factored form of the equation with the condition,
y = (x + 2) (x - 1) (x -8) + 48
y = (x² + x - 2) (x - 8) + 48
y = x³ + x² -2x -8x² -8x + 16 + 48
y = x³ - 7x² - 10x + 64
Therefore, the equation is y = x³ - 7x² - 10x + 64.
To learn more about the cubic equation;
brainly.com/question/13730904
#SPJ1
HELP ME ITS JUST SIMPLE STUFF (7th) I DONT KNOW IF I HAVE THE RIGHT ANSWER RN
Evaluate 12x - 7
If X=3
Choices-
1. 29
2. 43
3. 116
4. 120
-
Answers
Answer:
29
Step-by-step explanation:
Ok so with there being an X beside the number you go ahead and multiply the X and the number its beside (12) so 12x3=36 then you subtract 7 from 36 which will get you 29 hope this helped!
\((\frac{3p}{7}+\frac{7}{6p})^2 -(\frac{3p}{7}-\frac{7}{6p})^2\)
Solve with steps please
ty :)
Answers
Answer:
The expression simplifies to:
\((\frac{3p^2 + 49}{42p})^2 -(\frac{3p^2 - 49}{42p})^2\)
Using the difference of squares identity, the expression further simplifies to:
\(\frac{98p}{42p^2} = \frac{98}{42p}\)
Step-by-step explanation:
100 POINTS PLEASE HELP FAST
Select the correct answer.
The weight of a radioactive isotope was 96 grams at the start of an experiment. After one hour, the weight of the isotope was half of its initial weight. After two hours, the weight of the isotope was half of its weight the previous hour. If this pattern continues, which of the following graphs represents the weight of the radioactive isotope over time?

Answers
The top left graph represents the weight of the radioactive isotope over time.
How to define an exponential function?An exponential function has the definition presented according to the equation as follows:
\(y = ab^x\)
In which the parameters are given as follows:
a is the value of y when x = 0.b is the rate of change.The parameter values for the function in this problem are given as follows:
a = 96, b = 0.5.
Hence the function is given as follows:
\(y = 96(0.5)^x\)
Two points on the graph of the function are given as follows:
(1,48) and (2, 24).
Hence the top left graph represents the weight of the radioactive isotope over time.
More can be learned about exponential functions at brainly.com/question/2456547
#SPJ1
Answer:
Graph W
Step-by-step explanation:
The given information describes a radioactive decay process, where the weight of the isotope decreases by half at regular intervals. This type of decay is characteristic of exponential decay.
Based on the description, the graph that represents the weight of the radioactive isotope over time would be a decreasing exponential curve, where the y-axis represents the weight of the isotope (in grams), and the x-axis represents time (in hours).
The initial weight of the isotope is 96 grams, and after each subsequent hour, the weight becomes half of what it was in the previous hour. Therefore, the correct graph would start at 96 grams (the initial weight when x = 0) and then decrease by half every hour. It would be a curve that gets closer and closer to zero but never quite reaches it.
Initial weight: 96 grams
After 1 hour: 96 / 2 = 48 grams
After 2 hours: 48 / 2 = 24 grams
After 3 hours: 24 / 2 = 12 grams
After 4 hours: 12 / 2 = 6 grams
After 5 hours: 6 / 2 = 3 grams
So, the points on the graph would be:
(0, 96), (1, 48), (2, 24), (3, 12), (4, 6), (5, 3)Therefore, the graph that represents the weight of the radioactive isotope over time is Graph W.

evaluate each expression |-16| - |4|
Answers
Match the corresponding graph with the number. Note:a number can have multiple graphs.

Answers
(6) A function is increasing when the y-value increases as the x-value increases.
The domain is the set of allowable x-values
The following graphs increases over their entire domain:
B, E, I, J, N, G
(7) A function is said to be decreasing when the y-value decreases as the x-values increase.
The following graphs decreases over their entire domain:
A, F
5z + 3y = 4
-2x -8y = 6

Answers
Answer:
To eliminate a variable, you need to choose a strategy that allows you to add or subtract the equations in such a way that one variable will be eliminated. Let's go through the given options to determine the correct strategy:
A. Multiply the first equation by 2. Then add the equations.
If you multiply the first equation by 2, you get 10x + 6y = 8. If you add this equation to the second equation, you will not be able to eliminate either variable, as the coefficients of x and y do not match.
B. Multiply the first equation by 5 and the second equation by 2. Then add the equations.
If you multiply the first equation by 5, you get 25x + 15y = 20. If you multiply the second equation by 2, you get -4x - 16y = 12. Adding these equations gives you 21x - y = 32. This strategy allows you to eliminate y.
C. Multiply the second equation by 5. Then add the equations.
If you multiply the second equation by 5, you get -10x - 40y = 30. If you add this equation to the first equation, you will not be able to eliminate either variable, as the coefficients of x and y do not match.
D. Multiply the first equation by 2 and the second equation by 5. Then add the equations.
If you multiply the first equation by 2, you get 10x + 6y = 8. If you multiply the second equation by 5, you get -10x - 40y = 30. Adding these equations gives you -34y = 38. This strategy allows you to eliminate x.
Based on the options given, the correct strategy to eliminate a variable in this system of equations is: B.) Multiply the first equation by 5 and the second equation by 2. Then add the equations.
Aman borrowed rs.30,000 for 2 years at 10% P.A compounded annually. he paid only half of the principle at the end of 2 years. He paid the remaining principle and interest at the same rate at the end of the next 2 years. How much amount did he pay. Atlast to clear the debt??
Answers
The amount Aman paid to clear the debt, at last, was Rs. 25,773, including compounded interest of Rs.10,773.
What is compound interest?Compound interest is a type of interest system in that accumulated interest attracts interest.
With compounding, interest is paid on interest, unlike the simple interest system.
To compute compound interest, we use the following formula: CI = P( 1 + r/100)^n - P, where CI is compound interest, P is the principal, r is the compound interest rate and n is the number of years.
The amount of the loan = Rs.30,000
Loan period = 4 years
Annual percentage rate = 10%
Compounding period = Annual
Amount after two years = P( 1 + r/100)^n
= Rs. 30,000 x (1 + 0.1)^2
Rs. 36,300 (Rs. 30,000 x 1.21)
Payment after two years = Rs.15,000 (Rs. 30,000 x 50%)
Balance = Rs. 21,300 (Rs. 36,300 - Rs. 15,000)
Amount after another two years = Rs. 21,300 x (1 + 0.1)^2
= Rs. 25,773 ($21,300 x 1.21)
Total payments = Rs. 40,773 (Rs. 25,773 + Rs. 15,000)
Compounded interest = Rs. 10,773 (Rs. 40,773 - Rs. 30,000)
Thus, to settle the loan, lastly, Aman paid Rs. 21,300.
Learn more about compounding interest at https://brainly.com/question/28020457
#SPJ1
I need help on one more problem and thank you. I partially understand how to do this just a little more explaining could help.
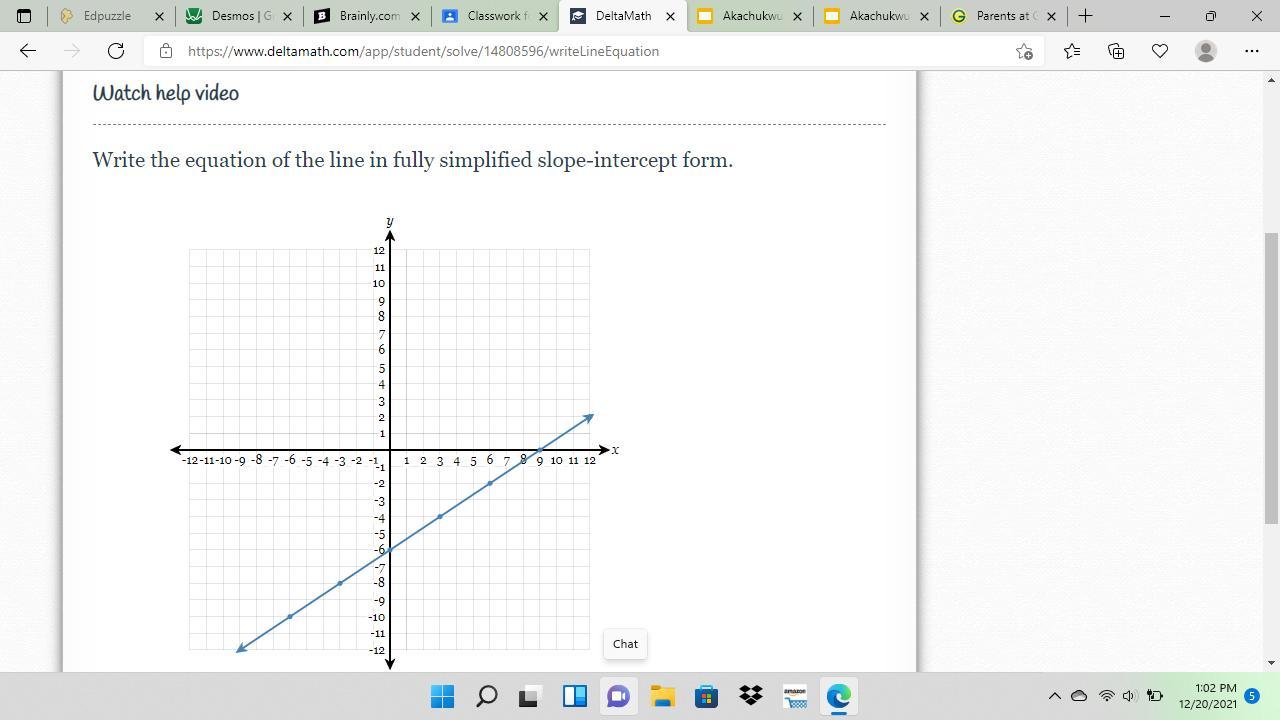
Answers
So,
To find the equation of the line given, we are going to follow the steps:
1. Identify two points that lie on the line.
As you can see, we could take the points (3 , -4) and (6 , -2).
2. Find the slope between both points. The slope is just the divition of the change of y-units between the points and the change of x-units between the points.
This, is:
3. We could use the main equation of a line:
\(y=mx+b\)Where m is the slope and (x,y) is a point that lie on the line.
What we're going to do, is to replace a point (x,y) and the slope that we just found so we can find the value of b and replace these values to find the equation.
So, let's replace (x,y) = (6,-2) and m=2/3:
\(\begin{gathered} y=mx+b \\ -2=\frac{2}{3}(6)+b \\ -2=4+b \\ b=-6 \end{gathered}\)Now, replace m and b in the equation for slope-intercept form:
\(y=mx+b\to y=\frac{2}{3}x-6\)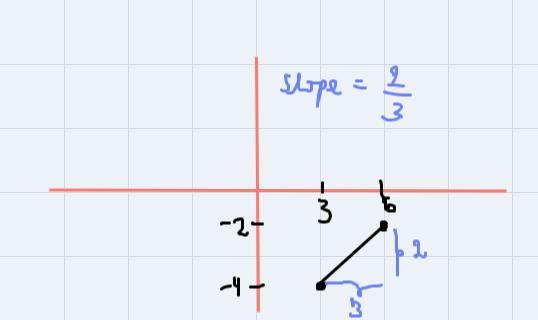
Find the amount of air needed to fill a basketball whose diameter is 9.45 in. Use 3.14 for
Answers
Answer:
The amount of air needed to fill the basketball is approximately 533.16 cubic inches
Step-by-step explanation:
To find the amount of air needed to fill a basketball, we need to first calculate its volume. We can use the formula for the volume of a sphere, which is V = (4/3)πr^3, where π is approximately 3.14 and r is the radius of the sphere.
Since the diameter of the basketball is given, we need to first find the radius by dividing the diameter by 2:
r = 9.45 in / 2 = 4.725 in
Now we can plug in the value of r into the formula for the volume:
V = (4/3)πr^3 = (4/3)π(4.725 in)^3 = 533.16 in^3
Therefore, the amount of air needed to fill the basketball is approximately 533.16 approx cubic inches.
To learn more about the amount of air to fill a basketball
https://brainly.com/question/20592924?referrer=searchResults
https://brainly.com/question/16606259?referrer=searchResults
URGENT!!! Find the surface area of the regular pyramid to the nearest hundredth.

Answers
Answer:
632.83mm²
Step-by-step explanation:
Applying Pythagorean theorem to triangle SOH
SH² = SO² + OH²
SH = \(\sqrt{(15.4)^2+(7.2)^2}=17mm\)
Since the base of the pyramid is a regular pentagon, angle OAH
is 108°/2 = 54°.
AH = 7.2/tan 54° = 5.23mm
So AB = 2AH = 10.46mm
The area of triangle SAB is:
A1 = 1/2 × SH × AB = 1/2 × 17 × 10.46 = 88.91mm²
The area of all triangles is
A2 = 5 × A1 = 5 × 88.91 = 444.55mm²
The area of the base is:
A3 = (perimeter × apothem)/2 = (5 × 10.46 × 7.2)/2 = 188.28mm²
The surface area of the pyramid is:
A2 + A3 = 444.55 + 188.28 = 632.83mm²

Step-by-step explanation:
the surface area is the sum of the base area (pentagon) and the 5 side triangles (we only need to calculate one and then multiply by 5, as they are all equal).
these side triangles are isoceles triangles (the legs are equally long).
the usual area formula for a pentagon is
1/2 × perimeter × apothem
the apothem is the minimum distance from the center of the pentagon to each of its sides.
in our case this is 7.2 mm.
how to get the perimeter or the length of an individual side of the pentagon ?
if the apothem of a pentagon is given, the side length can be calculated with the formula
side length = 2 × apothem length × tan(180/n)
where 'n' is the number of sides (5 in our case). After getting the side length, the perimeter of the pentagon can be calculated with the formula
perimeter = 5 × side length.
so, in our case
side length = 2 × 7.2 × tan(180/5) = 14.4 × tan(36) =
= 10.4622124... mm
perimeter = 5 × 10.4622124... = 52.31106202... mm
area of the pentagon = 1/2 × perimeter × apothem =
= 1/2 × 52.31106202... × 7.2 = 188.3198233... mm²
now for the side triangles.
the area of such a triangle is
1/2 × baseline × height
baseline = pentagon side length
height we get via Pythagoras from the inner pyramid height and the apothem :
height² = 7.2² + 15.4² = 51.84 + 273.16 = 289
height = 17 mm
area of one side triangle =
1/2 × 10.4622124... × 17 = 88.92880543... mm²
all 5 side triangles are then
444.6440271... mm²
and the total surface area is then
444.6440271... + 188.3198233... = 632.9638504... mm²
≈ 632.96 mm²
A police car traveling south toward Sioux Falls, Iowa, at 160 km/h pursues a truck traveling east away from Sioux Falls at
140 km/h.
At time t = 0, the police car is 60 km north and the truck is 50 km east of Sioux Falls.
Calculate the rate at which the distance between the vehicles is changing at t = 10 minutes.
(Use decimal notation. Give your answer to three decimal places.)
Answers
Using the Pythagorean Theorem, the rate at which the distance between the vehicles is changing at t = 10 minutes is of -20 km/hour.
What is the Pythagorean Theorem?The Pythagorean Theorem relates the length of the legs \(l_1\) and \(l_2\) of a right triangle with the length of the hypotenuse h, stating that the hypotenuse squared is the sum of the legs squared, according to the equation given below:
\(h^2 = l_1^2 + l_2^2\)
In the context of this problem, the distances of the cars from Sioux Falls, considering the initial distances and the velocities, are given as follows:
Police: P(t) = 60 - 160t.Truck: T(t) = 50 + 140t.The distance after t hours is the hypotenuse of a right triangle in which the legs are the functions, hence:
D²(t) = P²(t) + T²(t).
Hence the rate of change of the distance after t hours is:
2D'(t) = 2P'(t) + 2T'(t)
Simplifying by 2:
D'(t) = P'(t) + T'(t).
Applying the exponent rules, the derivatives are given as follows:
P'(t) = -160.T'(t) = 140.Hence the constant rate is:
D'(t) = -160 + 140 = -20 km/hour.
Meaning that the police car is getting 20 km closer to the truck each hour.
More can be learned about the Pythagorean Theorem at https://brainly.com/question/343682
#SPJ1
Un coche tarda 12 minutos en dar la vuelta a un circuito si va a una velocidad de 80 km/h. Cuánto tiempo tardara en recorrer el mismo circuito si va a una velocidad de 100 km/h?
Answers
A sample of matter experiences a decrease in average kinetic energy as it continues to cool. One would anticipate that the particles will eventually come to a complete stop. The temperature at which particles should theoretically stop moving is absolute zero. Thus, option B is correct.
What theory directly contradicts concept of absolute zero?
All molecules are predicted to have zero kinetic energy and, as a result, no molecular motion at absolute zero (273.15°C). Zero is a hypothetical value (it has never been reached).
Absolute zero signifies that there is no kinetic energy involved in random motion. A substance's atoms don't move relative to one another.
Therefore, Kinetic energy because it can create heat which goes against the absolute zero. A gas molecule's kinetic energy tends to zero when the temperature reaches absolute zero.
Learn more about theory here:
brainly.com/question/18996125
#SPJ2
Which equation is true when the value of "y" is 3 ? PLEASE HELP. NO LINKS! A: 2y -3 =6
B: 3y -2 =6
C: 11y +4 = 37
D: 4y +11 =37
Answers
Explanation:
If we replaced y with 3 in choice A, then we get
2y-3 = 6
2(3)-3 = 6
6-3 = 6
3 = 6
which is a false statement. So choice A's solution is not y = 3. We can cross choice A off the list. The same applies with choices B and D as well.
Choice C is the answer because,
11y+4 = 37
11(3)+4 = 37
33+4 = 37
37 = 37
which is true. This confirms choice C.
How do you use the distributive property to remove the parentheses. From 5(10+w)

Answers
Answer: 50 + 5w
Step-by-step explanation:
Apply the 5 to both of the elements inside of the parenthesis. You can divide it up into two different values.
5(10) + 5(w)
After creating those values, solve the multiplication to get:
50 + 5w
issac is swimming in the ocean. he is 3 feet below the surface of the water sees a fish below him. he dives down to a depth of 11 feet. how far down did issac dive?
Answers
.......................

Answers
Answer:
Direct variation
Step-by-step explanation:
Given
\(\frac{a_1}{b_1} = \frac{a_2}{b_2}\)
Required
The type of variation
The given equation represents a direct variation.
A direct variation is:
\(a = kb\)
Where
\(k\to\) constant of variation
Make k the subject
\(k = \frac{a}{b}\)
For corresponding values of and b, we have:
\(k = \frac{a_1}{b_1} = \frac{a_2}{b_2} = \frac{a_3}{b_3} = ............. =\frac{a_n}{b_n}\)
Hence, \(\frac{a_1}{b_1} = \frac{a_2}{b_2}\) is a direct variation
Simplify (-2x^3)2•y•y^9
Answers
-2x^3 • 2 = 4 (because 2•2 is 4, they don’t share the same variable so you just multiply the base)
y^9 • y^1 (9+1=10)
-4x^3 y^10
Simplify (-2x^3)^2 •y•y^9 Answer 4x^6y^10
(4,-8)and(6,-9) written in point-slope form,slope-intercept form, and standard form
Answers
Answer:
Point slope- y + 8 = − 1 2 ⋅ ( x − 4 )
Slope Intercept Form- y = − 1/ 2 x − 6
Slope- m=-1/2
Step-by-step explanation:
Point slope- y-y₁=m(x-x₁)
Slope Intercept form- y=mx+b\
Slope- rise/run= y2-y1/x2-x1
The mean life of a new smart LED bulb is 20,000 running hours with a standard deviation is 2,250 hours. The data is normally distributed. If a home improvement store sold 18,000 of these light bulbs in the first year of production, how many light bulbs would you expect to last longer than 22,250 hours?
Answers
Answer: The expected number of bulbs that would last longer than 22,250 hours is approximately 2,857.
Step-by-step explanation:
To solve this problem, we can start by finding the z-score for 22,250 using the formula:z = (x - mean) / standard deviationz = (22,250 - 20,000) / 2,250 = 1Next, we need to find the proportion of bulbs lasting longer than 22,250. We can look up this proportion in a standard normal distribution table or use a calculator, which gives us a probability of 0.1587.Finally, we can use this probability to find the expected number of bulbs that will last longer than 22,250:Expected number of bulbs = probability * total number of bulbs sold Expected number of bulbs = 0.1587 * 18,000 = 2,857Therefore, we can expect that approximately 2,857 of the 18,000 bulbs sold will last longer than 22,250 running hours.
Answer:
the afternoon is the right one
Find the equation of the line that contains the point (4,-2) and is perpendicular to the line y = – 2x + 5
Answers
Answer:
--2
Step-by-step explanation:
hope this helps if not sorry
Answer this math problem

Answers
\(\\ \sf{:}\dashrightarrow \dfrac{w^2}{25}+45w+155\)
w=1\(\\ \sf{:}\dashrightarrow \dfrac{52}{25}+45(52)+155\)
\(\\ \sf{:}\dashrightarrow \dfrac{52}{25}+2340+155\)
\(\\ \sf{:}\dashrightarrow \dfrac{52}{25}+2495\)
\(\\ \sf{:}\dashrightarrow 2+2495=2498\)
what is the distance between b and c?

Answers
Answer:
\(c = \sqrt{74}\)
Step-by-step explanation:
To find the distance between the two, we will use the Pythagorean theorem (\(a^{2} + b^{2} = c^{2}\)). To find a and b, we need to subtract the distances between the y coordinates and the x coordinates respectively. For the x coordinates, we have 8 - 1 = 7 units. For the y coordinates, we have 7 - 2 = 5. Plugging this into our equation gives us:
\(7^{2} + 5^{2} = c^{2}\)
We will simplify our exponents:
\(49 + 25 = c^{2}\)
Then adding them together gives us:
\(74 = c^{2}\)
Then, we square root both sides giving us:
\(\sqrt{74} = c\)
Then, we cannot simplify past this, since 74's prime factorization doesn't allow it. So, \(c = \sqrt{74}\).
Hope this helped!
Trapezoids A B C D and E F G H are shown on the graph.

Answers
Answer:
Reflection across the x axis, and rotation 180 degrees clockwise about origin.
find the domain of 5x-2
Answers
Find the distance between M(4,−3) and N(−2,1) .
Answers
Answer:
√40 is answer
Step-by-step explanation:
distance between 2points =√(x2-x1)²+ (y2-y1)
=√(2+4)²+(-1+3)²
=√62+22
=√36+4
mark as brainlist
=√40