Harry has 5 markers in a backpack. One of them is pink and one is
gray. What is the probability Harry will reach into the backpack without
looking and grab the pink marker and then reach in a second time and
grab the gray marker if:
(a) the first marker is not replaced?
(b) the first marker is replaced?
Answers
The required probabilities are 0.05 and 0.0625, respectively.
What is Probability?Probability helps us to know the chances of an event occurring. The sum of all the probabilities of an event is always equal to 1. The formula for probability is given as,
\(\rm Probability=\dfrac{Desired\ Outcomes}{Total\ Number\ of\ outcomes\ possible}\)
Given that Harry has 5 markers in a backpack. One of them is pink and one is gray.
Now, the probability that Harry will reach into the backpack without
looking and grab the pink marker and then reach in a second time and
grab the gray marker if the first marker is not replaced is,
Probability = (1/5) × (1/4)
= 0.20 × 0.25
= 0.05
Further, the probability that Harry will reach into the backpack without
looking and grab the pink marker and then reach in a second time and
grab the gray marker if the first marker is replaced is,
Probability = (1/5) × (1/5)
= 0.25 × 0.25
= 0.0625
Hence, the required probabilities are 0.05 and 0.0625, respectively.
Learn more about Probability here:
https://brainly.com/question/795909
#SPJ1
Related Questions
Find the measure of the red angle.

Answers
Answer:
Its 24! hope this helped!
Answer:
45 degrees.
I hope I'm right.
An arithmetic sequence has common difference d. the series sums s2, s5 and s7 themselves form an arithmetic sequence. find, in terms of d, the common difference for this sequence.
Answers
To find the common difference for the arithmetic sequence formed by the series sums s2, s5, and s7, let's analyze the given information.
The sum of the second term (s2), fifth term (s5), and seventh term (s7) themselves form an arithmetic sequence.
Let's denote the second term as a + 2d, the fifth term as a + 5d, and the seventh term as a + 7d, where 'a' is the first term and 'd' is the common difference.
Using the arithmetic sequence formula for the sum of terms, we have:
s2 = (2/2) * (2a + (2-1)d) = 2a + d
s5 = (5/2) * (2a + (5-1)d) = 5a + 6d
s7 = (7/2) * (2a + (7-1)d) = 7a + 12d
Since the sums s2, s5, and s7 themselves form an arithmetic sequence, we can express their differences:
s5 - s2 = (5a + 6d) - (2a + d) = 3a + 5d
s7 - s5 = (7a + 12d) - (5a + 6d) = 2a + 6d
Now, equating the differences, we have:
3a + 5d = 2a + 6d
Simplifying the equation, we find:
a = d
Therefore, the common difference for the arithmetic sequence formed by the series sums s2, s5, and s7 is 'd'.
Learn more about arithmetic here:
https://brainly.com/question/16415816
#SPJ11
The graph of a system of inequalities is shown.
On a coordinate plane, 2 straight lines are shown. The first solid line has a negative slope and goes through (negative 6, negative 1) and (0, negative 4). Everything below the line is shaded. The second dashed line has a positive slope and goes through (negative 2, negative 4) and (0, 0). Everything to the left of the line is shaded.
Which system is represented by the graph?
y > 2x
x + 2y ≤ –8
y ≥ 2x
x + 2y –8

Answers
Answer:
d
Step-by-step explanation:
Answer:
A
Step-by-step explanation:
E2021
Find the inverse matrix or type
"none". (Use decimals)
3
2
4
1
? ]
Enter
![Find the inverse matrix or type"none". (Use decimals)3241? ]Enter](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/2d2eLTj54WUrOy3HxLzDnz8tgFFMZRZY.png)
Answers
Answer:
\(\left[\begin{array}{cc}-0.2&0.4\\0.8&-0.6\end{array}\right]\)
Step-by-step explanation:
\(\left[\begin{array}{cc}3&2\\4&1\end{array}\right] ^{-1} =\frac{1}{3*1-2*4} \left[\begin{array}{cc}1&-2\\-4&3\end{array}\right]=(-0.2)*\left[\begin{array}{cc}1&-2\\-4&3\end{array}\right]=\left[\begin{array}{cc}-0.2&0.4\\0.8&-0.6\end{array}\right]\\\)
assume that the 13 employees consist of eight men and five women and that the assignments to day and night shifts are made at random. what is the probability that all four of the night-shift employees are men? round your answer to at least four decimal places. theprobabilitythatallfourofthenight-shiftemployeesaremenis.
Answers
The probability that all four of the night-shift employees are men is found to be 0.097.
The total number of employees are 13. The number of women and men employees are eight and five respectively.
The probability of an event is,
P(E) = Total favorable outcomes/total number of possible outcomes.
Here in this case,
The total possible outcomes are 13C4,
So, we get, total possible outcomes = 715
Total favorable outcome are 8C4,
So, we get, total favorable outcomes = 70
Probability that all the employees working at night are men is,
P(E) = 70/715
P(E) = 0.097
So, the probability that all four night shift employees are men is 0.097.
To know more about probability, visit,
https://brainly.com/question/24756209
#SPJ4
Evaluate the expression: 3/5+2^2−2/5(8−6)÷3

Answers
Answer:
Exact value: 13/3
Mixed number form: 4 1/3
Step-by-step explanation:
Answer:
B. 4 1/3
Step-by-step explanation:
just did this on T4L
y = 4sin 2x – 5cos 3x
Answers
Answer:
2π|b| 2 π | b
Step-by-step explanation:
Plz help me, i need this done 2 get my phone back

Answers
Answer:
Step-by-step explanation:
4x = 3yz^2
4x/3y = z^2
To undo an exponent you root it.
\(\sqrt{4x/3y} = z\)
I believe this is it. you basically just have to divide by the numbers to get z by itself. If you have any questions please comment.
A street sign is 14 inches long. A scale drawing of the sign is 5 inches long. What is the scale factor
Answers
Answer:
5/14
Step-by-step explanation:
A street sign is 14 inches long. A scale drawing of the sign is 5 inches long. What is the scale factor
Scale factor is calculated as:
Scale drawing/Street sign
= 5 inches/14 inches
= 5/14
Therefore, the scale factor 5/14
please help smart humans or aliens idc

Answers
the Answer is: (2,1)
Step-by-step explanation:
A probability is a numerical value that indicates the chance, or likelihood, of a specific event occurring.
Select one:
True
False
Answers
This statement is true
A probability is a numerical value that indicates the chance, or likelihood, of a specific event occurring. Probability is the measure of the likelihood of a random event happening, and it is expressed as a number between 0 and 1, with 0 implying that the event would never occur and 1 implying that it is certain to happen.
The probability of an event happening is referred to as its likelihood. Probability can be expressed as a fraction, percentage, or decimal, and it is a vital tool in statistics. It is frequently utilized in mathematics to estimate real-world situations that involve random variables such as coin flips, weather patterns, stock market trends, and even sporting events.
Learn more about probability
https://brainly.com/question/31828911
#SPJ11
In a set of 10 observations the mean is 20 and the median is 15. There are 2 values that are 6, and all other values are different. What is the mode?
Answers
The mode of the set of 10 observations is 2.
What is the mode?
Mode refers to a value that appears most frequently in a data set. Mode is a measure of central tendency of a data set. Other measures of central tendency are mean and median.
According to the information in the question, 6 appears twice in the data set and all other values are different. Thus, 6 has the frequency of 2 which is the highest. 6 is the mode.
To learn more about mode, please check: https://brainly.com/question/16505756
#SPJ1
a researcher is interested in the relationship between happiness and gpa of high school students. after surveying 50 students, he determines that there is a correlation between these two variables of .90. this is considered a: group of answer choices strong negative linear correlation strong positive linear correlation weak negative linear correlation weak positive linear correlation
Answers
The correlation coefficient of 0.90 indicates a strong positive linear correlation between happiness and GPA of high school students.
A correlation coefficient measures the strength and direction of the relationship between two variables. In this case, the correlation coefficient of 0.90 indicates a strong positive linear correlation between happiness and GPA of high school students.
A positive correlation means that as one variable (in this case, happiness) increases, the other variable (GPA) also tends to increase. The magnitude of the correlation coefficient, which ranges from -1 to 1, represents the strength of the relationship. A value of 0.90 indicates a very strong positive linear correlation, suggesting that there is a consistent and significant relationship between happiness and GPA.
This means that as the level of happiness increases among high school students, their GPA tends to be higher as well. The correlation coefficient of 0.90 suggests a high degree of predictability in the relationship between these two variables.
It is important to note that correlation does not imply causation. While a strong positive correlation indicates a relationship between happiness and GPA, it does not necessarily mean that one variable causes the other. Other factors or variables may also influence the relationship between happiness and GPA.
Learn more about: Coefficient
brainly.com/question/1594145
#SPJ11
The combined perimeter of an equilateral triangle and square is 13.
Find the dimensions of the triangle and square that produce a minimum total area.
The measurement of square on each side
The measurement of triangle on each side
Find the dimensions of the triangle and square that produce a maximum total area.
The measusrement of square on each side
The measurement of triangle on each side
Answers
To minimize the total area of an equilateral triangle and square, the side length of the square should be 2.167 and the side length of the triangle should be 3.833.
To find the dimensions that minimize the total area, we can set up equations based on the given information. Let's denote the side length of the square as 's' and the side length of the equilateral triangle as 't'. The perimeter of the square is 4s, and the perimeter of the equilateral triangle is 3t. Given that the combined perimeter is 13, we have the equation 4s + 3t = 13.
To minimize the total area, we need to consider the formulas for the areas of the square and equilateral triangle. The area of the square is given by A_square = \(s^2\), and the area of the equilateral triangle is given by A_triangle = (\(\sqrt{(3)}\)/4) *\(t^2\).
To find the values that minimize the total area, we can substitute s = (13 - 3t)/4 into the equation for A_square and solve for t. By finding the derivative of the total area with respect to t and setting it equal to zero, we can find the value of t that minimizes the area.
Similarly, to find the dimensions that maximize the total area, we follow the same process but this time maximize the total area by finding the value of t that maximizes the area.
Performing the calculations, we find that to minimize the total area, the side length of the square is approximately 2.167 and the side length of the triangle is approximately 3.833. To maximize the total area, the side length of the square is approximately 4.333 and the side length of the triangle is approximately 1.667.
Learn more about equilateral triangle here:
https://brainly.com/question/30176141
#SPJ11
Use the diagram below to answer the following prompts.
What are the slopes of DE and AC?
Prove DE is 1/2 of AC?
Explain how the above makes DE the midsegment of ∆ABC.

Answers
The slopes for each segment are given as follows:
DE = 0.AC = 0.The lengths of each segment are given as follows:
DE = 4.AC = 8.Hence DE = 0.5 = AC, and thus DE is the midsegment of triangle ABC.
How to calculate the slopes?The slope of a set of two points is given by the change in y between the two points divided by the change in x between the two points.
Both segments in this problem, DE and AC, are horizontal lines, meaning that the change in y is of zero while the change in x is different of zero, thus the slope is calculated as follows:
Slope = Zero/Constant different of Zero = Zero.
The lengths of each of the horizontal segments is obtained subtracting the x-coordinates, as follows:
DE = 5 - 1 = 4 units.AC = 8 - 0 = 8 units.More can be learned about slopes at https://brainly.com/question/8062156
#SPJ1
On a house blueprint, 2 feet is represented by 1inch. If a room on the blueprint measures 5 inches by 6 inches, what is the area of the actual room?
Answers
Answer:
the answer is 120 feet
Step-by-step explanation:
It takes a train going 50 mph approximately _____ to stop safely.
A. 100 ft B. 1/2 miles C. 1 1/2 miles D. 5 miles
Answers
It takes a train going 50 mph approximately 11/2 miles to stop safely.
The distance a train takes to come to a stop can be determined by several factors, including the speed of the train, the weight of the train, the condition of the brakes and the track, and the reaction time of the engineer.
In general, a train going 50 mph will take about 1 1/2 miles or 8,000 feet to stop safely. This is because a train moving at 50 mph is traveling at about 75 feet per second, and it takes a significant distance to slow down a heavy object moving at such a high speed. It's important to note that this is an estimation, and the actual stopping distance may vary depending on the specific conditions.
To know more about Speed:
https://brainly.com/question/28224010
#SPJ4
The age to which a person in a particular cohort is statistically likely to live on the basis of average longevity of a population is known as
Answers
The age to which a person in a particular cohort is statistically likely to live on the basis of average longevity of a population is known as life expectancy.
Life expectancy is a measure of how long individuals from a specific population are expected to live, on average.
It is influenced by various factors such as healthcare access, lifestyle choices, socioeconomic status, and genetic predispositions.
Life expectancy is typically calculated using statistical models based on mortality rates and population data.
It is an important indicator used by policymakers, healthcare professionals, and researchers to assess the overall health and well-being of a population.
In conclusion, life expectancy provides insights into the expected lifespan of individuals in a population, helping to inform decisions related to public health and social policy.
To know more about population visit;
brainly.com/question/15889243
#SPJ11
An apple orchard's workers pick 12,500 apples in the month of October. A sample of 300 of these apples shows that 15 of them are damaged and bruised.
What is the best estimate of the number of apples picked at the orchard in October that are bruised and damaged?
Question 18 options:
42
625
750
1875
Answers
Answer:
625
Step-by-step explanation:
Convert 15300 to a percent,
We can convert it to it's lowest fraction,
120, and to find the percent just multiply it by 5 on top and bottom,
120 ×5×5
which equals, 5100
Then take the percent as a decimal, 0.5 and multiply it by 12500,
12500×0.5 which would give you: 625
What is the vertex for the equation y=2x^2+4x
Answers
The simplest factorial design contains:
A. 1 independent variable with 2 conditions
B. 2 independent variables with 2 conditions
C. 2 independent variables with 3 conditions
D. 3 independent variables with 2 conditions
Answers
The simplest factorial design contains 2 independent variables with 2 conditions. The answer is option B.
A factorial design is a study in which two or more independent variables are manipulated to see their impact on the dependent variable. The simplest factorial design contains two independent variables, each with two conditions, for a total of four conditions. This is referred to as a 2x2 factorial design. The factors analyzed in such a design are the primary factor: Factor A, which has two levels, is known as the primary factor or the rows, and the secondary factor: Factor B, which has two levels, is referred to as the secondary factor or the columns.
Learn more about factorial design:
brainly.com/question/28146573
#SPJ11
Is 1/19 a rational number?
Answers
Answer:
Yes.
Step-by-step explanation:
It is a fraction.
1. The equations of demand and supply of a product are:120 p-q-240 = 0100p+q-1200 = 0 respectively.A. Find the equilibrium price

Answers
Datos:
Oferta:
\(120p-q-240=0\)Demanda:
\(100p+q-1200=0\)Para encontrar el precio de equilibrio iguala las ecuaciones de oferta y demanda:
\(120p-q-240=100p+q-1200\)El precio de equilibrio lo encuentras resolviendo la ecuación arriba para p(precio):
1.
\(120p-240=100p-1200\)2. Para dejar los terminos con la variable p de un lado de la ecuacion resta 100p en los dos lados de la ecuacion:
\(120p-100p-240=100p-100p-1200\)A factory that makes gaming systems selects 250 random systems to check for defects. They find that 25 out of the gaming systems were defective and had to be discarded.
How many gaming systems out of 3000 should the factory predict will be defective?
Answers
Answer:
300
Step-by-step explanation:
can someone please answer this with step by step see picture. thank you

Answers
Answer:
The value of x = 40.
Step-by-step explanation:
From the figure, it is clear that given a transversal line cuts two parallel lines m and n, thus making the corresponding congruent angles 120° and 3x°.
Here, 120° is corresponding to 3x°.
As corresponding angles are congruent.
so
3x° = 120°
Divide both sides by 3
3x/3 = 120 / 3
x = 40
Therefore, the value of x = 40.
Use the simplex algorithm to find the optimal solution to the following LP (solve manually): maxz= 36x1+30x2−3x3−4x4
s.t. x1+x2−x3≤5
6x1+5x2−x4≤10
∀xi≥0
Answers
The maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
maximize: z = c1x1 + c2x2 + ... + cnxn
subject to
a11x1 + a12x2 + ... + a1nxn ≤ b1
a21x1 + a22x2 + ... + a2nxn ≤ b2
am1x1 + am2x2 + ... + amnxn ≤ bmxi ≥ 0 for all i
In our case,
the given LP is:maximize: z = 36x1 + 30x2 - 3x3 - 4x
subject to:
x1 + x2 - x3 ≤ 5
6x1 + 5x2 - x4 ≤ 10
xi ≥ 0 for all i
We can rewrite the constraints as follows:
x1 + x2 - x3 + x5 = 5 (adding slack variable x5)
6x1 + 5x2 - x4 + x6 = 10 (adding slack variable x6)
Now, we introduce the non-negative variables x7, x8, x9, and x10 for the four decision variables:
x1 = x7
x2 = x8
x3 = x9
x4 = x10
The objective function becomes:
z = 36x7 + 30x8 - 3x9 - 4x10
Now we have the problem in standard form as:
maximize: z = 36x7 + 30x8 - 3x9 - 4x10
subject to:
x7 + x8 - x9 + x5 = 5
6x7 + 5x8 - x10 + x6 = 10
xi ≥ 0 for all i
To apply the simplex algorithm, we initialize the simplex tableau as follows:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0 | 36 | 30 | -3 | -4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | 0 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x6| 0 | 0 | 1 | 6 | 5 | 0 | -1 | 10 |
---------------------------------------------------------------------------
Now, we can proceed with the simplex algorithm to find the optimal solution. I'll perform the iterations step by step:
Iteration 1:
1. Choose the most negative coefficient in the 'z' row, which is -4.
2. Choose the pivot column as 'x10' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 5/0 = undefined, 10/(-4) = -2.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to
make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.4 | 36 | 30 | -3 | 0 | 12 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.2 | 1 | 1 | -1 | 0 | 5 |
---------------------------------------------------------------------------
x10| 0 | 0 | 0.2 | 1.2 | 1 | 0 | 1 | 2.5 |
---------------------------------------------------------------------------
Iteration 2:
1. Choose the most negative coefficient in the 'z' row, which is -3.
2. Choose the pivot column as 'x9' (corresponding to the most negative coefficient).
3. Calculate the ratios (RHS / pivot column coefficient) to find the pivot row. We select the row with the smallest non-negative ratio.
Ratios: 12/(-3) = -4, 5/(-0.2) = -25, 2.5/0.2 = 12.5
4. Pivot at the intersection of the pivot row and column. Divide the pivot row by the pivot element to make the pivot element 1.
5. Perform row operations to make all other elements in the pivot column zero.
After performing these steps, we get the updated simplex tableau:
| Cj | x5 | x6 | x7 | x8 | x9 | x10 | RHS |
---------------------------------------------------------------------------
z | 0 | 0 | 0.8 | 34 | 30 | 0 | 4 | 0 |
---------------------------------------------------------------------------
x5| 0 | 1 | -0.4 | 0.6 | 1 | 5 | -2 | 10 |
---------------------------------------------------------------------------
x9| 0 | 0 | 1 | 6 | 5 | 0 | -5 | 12.5 |
---------------------------------------------------------------------------
Iteration 3:
No negative coefficients in the 'z' row, so the optimal solution has been reached.The optimal solution is:
z = 0
x1 = x7 = 0
x2 = x8 = 10
x3 = x9 = 0
x4 = x10 = 0
x5 = 10
x6 = 0
Therefore, the maximum value of z is 0, and the values of the decision variables are x1 = 0, x2 = 10, x3 = 0, x4 = 0.
Learn more about Simplex Algorithm here:
https://brainly.in/question/46895640
#SPJ11
How much water fills the prism and what’s the slant height ?
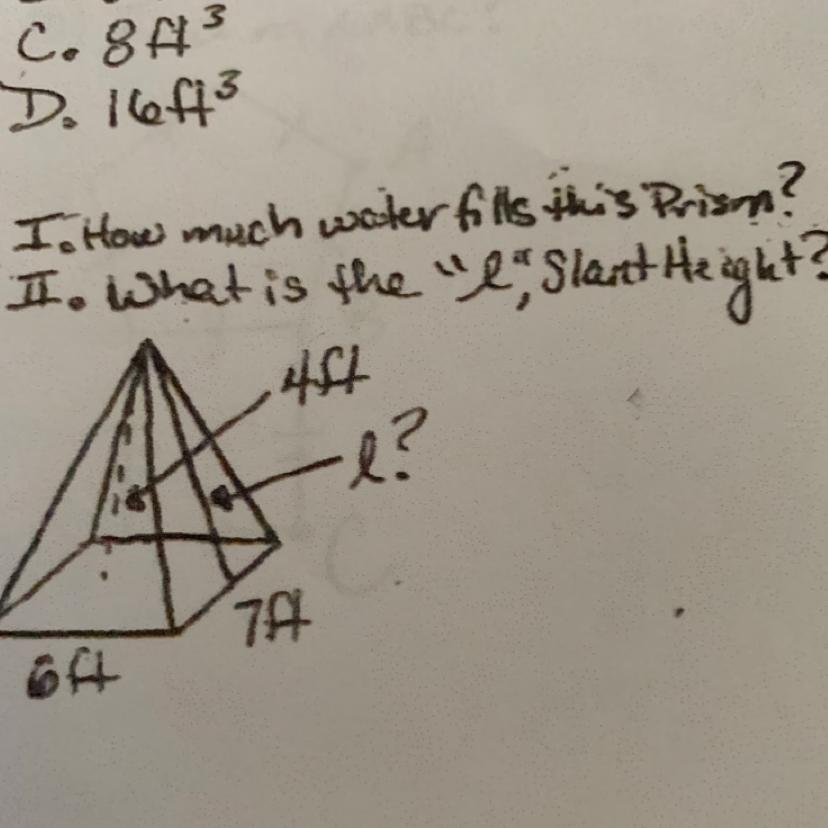
Answers
Answer:
I. 56 cubic feet of water.
II. 5 feet
Step-by-step explanation:
Which equation represents the line that is perpendicular to y=1/6 and passes through (-8,-2)?
Answers
Answer:
y = -6x - 50
Step-by-step explanation:
y = mx + b
Since it is perpendicular to y=1/6, the slope is -6. (Opposite reciprocal)
y = -6x + b.
Substitute to get: -2 = 48 + b
b = -50
y = -6x - 50
what is the mean for the data set 138 140 105 112 108 134 106 181 164 105
Answers
Answer:
the mean for the data set is 129.3
A tank of water in the shape of a cone is being filled with water at a rate of 12 m/sec. The base radius of the tank is 26 meters, and the height of the tank is 18 meters. At what rate is the depth of
Answers
The depth of the water in the cone-shaped tank is increasing at a rate of approximately 1.385 meters per second.
To determine the rate at which the depth of the water is changing, we can use related rates. Let's denote the depth of the water as h(t), where t represents time. We are given that dh/dt (the rate of change of h with respect to time) is 12 m/sec, and we want to find dh/dt when h = 18 meters.
To solve this problem, we can use the volume formula for a cone, which is V = (1/3)πr^2h, where r is the base radius and h is the depth of the water. We can differentiate this equation with respect to time t, keeping in mind that r is a constant (since the base radius does not change).
By differentiating the volume formula with respect to t, we get dV/dt = (1/3)πr^2(dh/dt). Now we can substitute the given values: dV/dt = 12 m/sec, r = 26 meters, and h = 18 meters.
Solving for dh/dt, we have (1/3)π(26^2) (dh/dt) = 12 m/sec. Rearranging this equation and solving for dh/dt, we find that dh/dt is approximately 1.385 meters per second. Therefore, the depth of the water in the tank is increasing at a rate of about 1.385 meters per second.
Learn more about volume of cone here: brainly.com/question/16419032
#SPJ11