Guided practice
it's not letter c. -2.6
state what number you would subtract from each side of the inequality to solve the inequality.
5.7 ≥ k + 3.1
a.
3.1
b.
5.7
c.
–2.6
Answers
The value of k that is less than or equal to 2.6
To solve the inequality 5.7 ≥ k + 3.1, you should subtract 3.1 from each side of the inequality.
To isolate the variable k, we need to perform the same operation on both sides of the inequality. In this case, we need to subtract 3.1 from each side:
5.7 - 3.1 ≥ k + 3.1 - 3.1
This simplifies to:
2.6 ≥ k
Therefore, the correct answer is:
k ≤ 2.6
We subtracted 3.1 from each side to isolate the variable k, resulting in the inequality k ≤ 2.6. This means that any value of k that is less than or equal to 2.6 will satisfy the original inequality 5.7 ≥ k + 3.1.
To learn more about variable, refer below:
https://brainly.com/question/17344045
#SPJ11
Related Questions
If you borrow $500 for 6 years at an
annual interest rate of 7%, how
much will you pay altogether?
Answers
If we borrowed $500 for 6 years at a rate of 7% interest then we will have to pay approximately $750 after 6 years.
Given that principal amount is $500 , years are 6 and rate of interest be 7%.
We are required to find the amount that we have to pay after 6 years if we borrow $500.
Compound interest is the interest that is calculated on the principal plus the accumulated interest at that point of time.
Sum after compounding is given as under:
S=P\((1+R)^{N}\)
So we have to just put the values to find the money that we have to pay after 6 years.
S=500\((1+0.07)^{6}\)
=500\((1.07)^{6}\)
=500*1.5
=$750
Hence if we borrowed $500 for 6 years at a rate of 7% interest then we will have to pay approximately $750 after 6 years.
Learn more about compound interest at https://brainly.com/question/24924853
#SPJ1
Evaluate:
3(w – x)?
where w = 5 and x = 2
Answers
Answer:
9
Step-by-step explanation:
just plug in the numbers
\(3(w - x), w=5, x=2\\ 3 \times (5 - 2) = 3 \times 3 = 9\)
Answer:
9
Step-by-step explanation:
a bank measures the wait time for a random sample of 15 customers during the lunch hour (measured in minutes). a hypothesis test is conducted to see if there is evidence that the average wait time is 5 minutes. what is the p-value for the test?
Answers
If a hypothesis test is conducted to see if there is evidence that the average wait time is 5 minutes, the p-value is 0.040.
To calculate the p-value for the hypothesis test, we need to perform the following steps:
Step 1: State the null and alternative hypotheses.
In this case, the null hypothesis (H0) is that the average wait time for customers during the lunch hour is 5 minutes. The alternative hypothesis (Ha) is that the average wait time is not 5 minutes.
Step 2: Determine the test statistic.
We can use a t-test since we do not know the population standard deviation. We calculate the t-value using the formula:
t = (x' - μ) / (s / √n)
where x' is the sample mean, μ is the population mean (5 minutes), s is the sample standard deviation, and n is the sample size (15).
Step 3: Calculate the p-value.
We can use a t-distribution table or software to find the p-value associated with our calculated t-value. Alternatively, we can use the t-test function in Excel or other statistical software to calculate the p-value directly.
Assuming a two-tailed test and a significance level of 0.05, if the p-value is less than 0.05, we reject the null hypothesis in favor of the alternative hypothesis. If the p-value is greater than 0.05, we fail to reject the null hypothesis.
Suppose the sample mean is 6.2 minutes, the sample standard deviation is 1.3 minutes, and the sample size is 15. Then the t-value is:
t = (6.2 - 5) / (1.3 / √15) = 2.22
Using a t-distribution table or software with 14 degrees of freedom (15 - 1), we find the p-value to be approximately 0.040, which is less than 0.05. Therefore, we reject the null hypothesis and conclude that there is evidence to suggest that the average wait time for customers during the lunch hour is not 5 minutes.
To learn more about sample click on,
https://brainly.com/question/15090400
#SPJ4

When x=-3, then y=______

Answers
Answer:-1
Step-by-step explanation:
Answer: -6
Step-by-step explanation:
the line pass through (-3,-6)
What is the value of z for the equation 1/2 z = - 3/4 + 1/4 ? (5 points)
Answers
Answer:
z = -1
Step-by-step explanation:
What is the value of x in the following figure?

Answers
Answer: x =11
Step-by-step explanation:
Find two consecutive numbers with a product of 9506.
Answers
Answer:
97 and 98
Step-by-step explanation:
Find the surface area of the cylinder and round to the nearest tenth. (Use the π button on your calculator)

Answers
The surface area of the cylinder with the given height and radius is 835.2 square inches
How to determine the surface area?The given parameters are
Height, h = 12 inches; this is represented by the distance between the curved surfaces of the cylinderRadius, r = 7 inches; this is represented by the distance between the center of the circle to its circumferenceThe surface area is then calculated using the following formula
A = 2πr² + 2πrh
Substitute the given values in the above equation
So, we have:
A = 2 * 3.14 * 7^2 + 2 * 3.14 * 7 * 12
Evaluate the exponents
A = 2 * 3.14 * 49 + 2 * 3.14 * 7 * 12
Evaluate the products
A = 307.72 + 527.52
Evaluate the sum
A = 835.2
Hence, the surface area of the cylinder with the given height and radius is 835.2 square inches
Read more about surface area at:
https://brainly.com/question/2835293
#SPJ1
Consider a biased coin that comes up ""heads"" 40% of the time. We flip this coin 100 times. Use the central limit theorem to approximate the probability that we will see more than 45 coin flips?
Answers
So, the approximate probability of seeing more than 45 coin flips as heads out of 100 flips is approximately 0.1539, or 15.39%.
To approximate the probability of seeing more than 45 coin flips as heads out of 100 flips, we can use the central limit theorem. The central limit theorem states that for a large enough sample size, the distribution of the sum (or average) of independent and identically distributed random variables approaches a normal distribution.
In this case, each coin flip is a Bernoulli trial with a probability of success (getting heads) of 0.4. We can consider the number of heads obtained in 100 flips as a sum of 100 independent Bernoulli random variables.
The mean of a single coin flip is given by μ = np = 100 * 0.4 = 40, and the standard deviation is given by σ = sqrt(np(1-p)) = sqrt(100 * 0.4 * 0.6) ≈ 4.90.
Now, to approximate the probability of seeing more than 45 coin flips as heads, we can use the normal distribution with the mean and standard deviation calculated above.
Let X be the number of heads in 100 flips. We want to find P(X > 45).
Using the standard normal distribution, we can calculate the z-score for 45 flips: z = (45 - 40) / 4.90 ≈ 1.02
Using a standard normal distribution table or a calculator, we can find the probability associated with this z-score: P(Z > 1.02) ≈ 1 - P(Z < 1.02)
Looking up the value in the table, we find that P(Z < 1.02) ≈ 0.8461.
Therefore, P(Z > 1.02) ≈ 1 - 0.8461 ≈ 0.1539.
So, the approximate probability of seeing more than 45 coin flips as heads out of 100 flips is approximately 0.1539, or 15.39%.
To know more about probability click here
brainly.com/question/15124899
#SPJ11
Find all missing angles.

Answers
Answer:
1= 41
2=85
3= 95
4=85
5= 36
6= 49
7= 188
Step-by-step explanation:
I think that's the answer
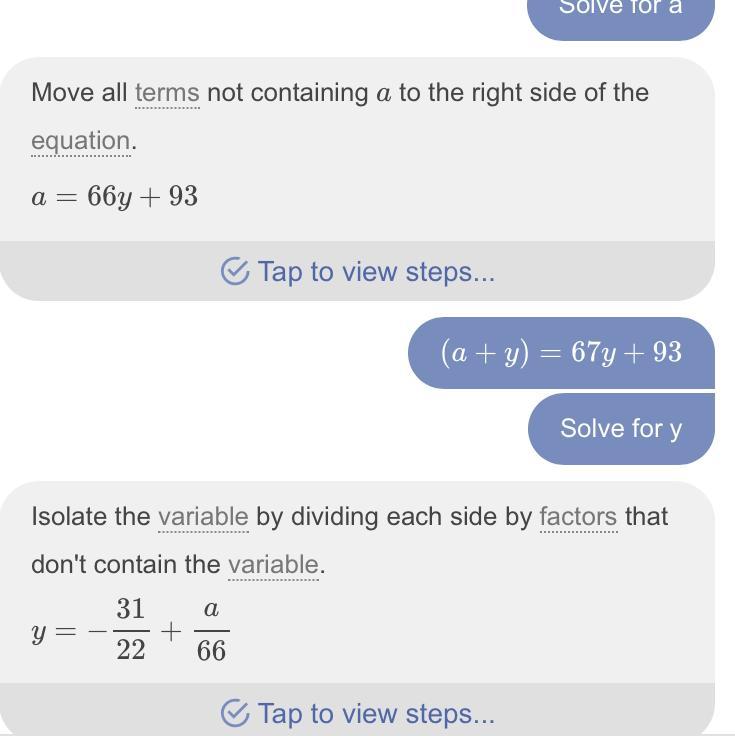
q⋅(a+y)=67y+93
what is the answer?
Answers
(a) Calculate Earth’s mass given the acceleration due to gravity at the North Pole is 9.830 m/s2 and the radius of the Earth is 6371 km from pole to pole. (b) Compare this with the accepted value of 5.979×1024 kg .
Answers
a) The given values: M = (9.830 * (6371000)^2) / (6.67430 × 10^-11)
M ≈ 5.970 × 10^24 kg
b) Comparing this with the calculated value from part (a), we can see that they are very close:
Calculated mass: 5.970 × 10^24 kg
Accepted mass: 5.979 × 10^24 kg
(a) To calculate Earth's mass given the acceleration due to gravity at the North Pole (g) and the radius of the Earth (r), we can use the formula for gravitational acceleration:
g = (G * M) / r^2
Where:
g = acceleration due to gravity (9.830 m/s^2)
G = gravitational constant (6.67430 × 10^-11 m^3/kg/s^2)
M = mass of the Earth
r = radius of the Earth (6371 km = 6371000 m)
Rearranging the formula to solve for M:
M = (g * r^2) / G
Substituting the given values:
M = (9.830 * (6371000)^2) / (6.67430 × 10^-11)
M ≈ 5.970 × 10^24 kg
(b) The accepted value for Earth's mass is approximately 5.979 × 10^24 kg.
Comparing this with the calculated value from part (a), we can see that they are very close:
Calculated mass: 5.970 × 10^24 kg
Accepted mass: 5.979 × 10^24 kg
The calculated mass is slightly lower than the accepted value, but the difference is within a reasonable margin of error.
Learn more about values here:
https://brainly.com/question/30145972
#SPJ11
The average resident of Metro City produces 630 pounds of solid waste each year, and the standard deviation is approximately 70 pounds. Use Chebyshev's theorem to find the weight range that contains at least of all residents' annual garbage weights.
Answers
The weight range that contains at least 75% of all residents' annual garbage goes between 420 pounds and 787.5 pounds.
AveragesGiven that the average resident of Metro City produces 630 pounds of solid waste each year, and the standard deviation is approximately 70 pounds, to determine the weight range that contains at least 75% of all residents' annual garbage weights, the following calculation must be performed:
630 - 70 = 560630 + 70 = 700560 x 0.75 = 420630 x 1.25 = 787.5Therefore, the weight range that contains at least 75% of all residents' annual garbage goes between 420 pounds and 787.5 pounds.
Learn more about averages in https://brainly.com/question/22801800
How are the roots of the equation x^2-2x-15=0 related to the function y=x^2-2x-15
Answers
Answer:
They are zeroes when y=0
Step-by-step explanation:
For a function \(f(x)\), if \(f(x)=0\), the values of x that make the function true are known as roots, or x-intercepts, or zeroes.
Find the volume of a frustum of a right circular cone with height 15, lower base radius 25 and top radius 19.
Answers
The volume of the frustum of the right circular cone is approximately 21850.2 cubic units where frustum of a cone is a three-dimensional geometric shape that is obtained by slicing a larger cone with a smaller cone parallel to the base.
To find the volume of a frustum of a right circular cone, we can use the formula:
V = (1/3) * π * h * (r₁² + r₂² + (r₁ * r₂))
where V is the volume, h is the height, r₁ is the radius of the lower base, and r₂ is the radius of the top base.
Given the values:
h = 15
r₁ = 25
r₂ = 19
Substituting these values into the formula, we have:
V = (1/3) * π * 15 * (25² + 19² + (25 * 19))
Calculating the values inside the parentheses:
25² = 625
19² = 361
25 * 19 = 475
V = (1/3) * π * 15 * (625 + 361 + 475)
V = (1/3) * π * 15 * 1461
V = (1/3) * 15 * 1461 * π
V ≈ 21850.2 cubic units
To know more about volume,
https://brainly.com/question/31815000
#SPJ11
The volume of the frustum of the right circular cone is approximately 46455 cubic units.
To find the volume of a frustum of a right circular cone, we can use the formula:
V = (1/3) * π * h * (R² + r² + R*r)
where V is the volume, π is a constant approximately equal to 3.14, h is the height of the frustum, R is the radius of the lower base, and r is the radius of the top base.
Given that the height (h) is 15 units, the radius of the lower base (R) is 25 units, and the radius of the top base (r) is 19 units, we can substitute these values into the formula.
V = (1/3) * π * 15 * (25² + 19² + 25*19)
Simplifying this expression, we have:
V = (1/3) * π * 15 * (625 + 361 + 475)
V = (1/3) * π * 15 * 1461
V ≈ (1/3) * 3.14 * 15 * 1461
V ≈ 22/7 * 15 * 1461
V ≈ 46455
Learn more about right circular cone
https://brainly.com/question/14797735
#SPJ11
Suppose X has a continuous uniform distribution over the interval [1.8, 5.4]. Round your answers to 3 decimal places. (a) Determine the mean of X. (b) Determine the variance of X. (c) What is P(X < 3.4)
Answers
Given: A continuous uniform distribution over the interval [1.8, 5.4].To find:(a) Mean of X.(b) Variance of X.(c) P(X < 3.4)
The following formula is used to determine the mean of X when its continuous uniform distribution falls within the range [a, b]. And X's variance is given by 2 = (b - a)2/12.
Part (a): Mean of X The given interval is [1.8, 5.4].So, a = 1.8 and b = 5.4By using the above formula of mean,μ = (a + b)/2μ = (1.8 + 5.4)/2μ = 3.6Hence, the mean of X is 3.6.
Part (b): Variance of X By using the formula of variance,σ² = (b - a)²/12σ² = (5.4 - 1.8)²/12σ² = (3.6)²/12σ² = 12.96/12σ² = 1.08Hence, the variance of X is 1.08.
Part (c): P(X < 3.4)We have to find P(X < 3.4)The given distribution is a continuous uniform distribution over the interval [1.8, 5.4].The probability density function for this is,f(x) = 1/(5.4 - 1.8)f(x) = 1/3.6We have to find P(X < 3.4) = P(1.8 ≤ X ≤ 3.4)
From the probability density function,f(x) = 1/3.6And we know that, P(a ≤ X ≤ b) = ∫[a,b] f(x) dxBy using this, we get,P(1.8 ≤ X ≤ 3.4) = ∫[1.8, 3.4] 1/3.6 dxP(1.8 ≤ X ≤ 3.4) = [x/3.6]1.8³.⁶ - 1.8P(1.8 ≤ X ≤ 3.4) = [3.4/3.6] - [1.8/3.6]P(1.8 ≤ X ≤ 3.4) = 0.56 - 0.50P(1.8 ≤ X ≤ 3.4) = 0.06. Hence, P(X < 3.4) = 0.06.
Learn more on variance here:
brainly.in/question/8403667
#SPJ11
Martha is currently age 55 who purchases a deferred whole life annuity-due policy which will pay her the following benefits : - Guaranteed annual payments of 8000 for 10 years, starting when she reaches age 60. - Annual payments of 30000 for the subsequent 10 years, if alive. - Annual payments of 85000 , if alive, thereafter. You are given : -Mortality follows the Standard Ultimate Survival Model. −i=5% Calculate the actuarial present value of Martha's life annuity benefits .
Answers
The actuarial present value of Martha's life annuity benefits is $497,531.59.
To calculate the actuarial present value of Martha's life annuity benefits, we need to discount each payment using the given interest rate and the probability of survival for each period.
Given:
- Guaranteed annual payments of $8,000 for 10 years, starting at age 60.
- Annual payments of $30,000 for the subsequent 10 years, if alive.
- Annual payments of $85,000, if alive, thereafter.
- Mortality follows the Standard Ultimate Survival Model.
- Interest rate (discount rate) is 5%.
We can break down the calculation into three parts:
1. Present value of the guaranteed annual payments of $8,000 for 10 years, starting at age 60:
We discount each payment using the interest rate of 5% and the probability of survival for each year. Since the mortality follows the Standard Ultimate Survival Model, we can use actuarial tables to obtain the survival probabilities. Assuming the survival probabilities are as follows:
Age 60: 0.9872
Age 61: 0.9756
Age 62: 0.9639
...
Age 69: 0.9172
The present value of the guaranteed payments is calculated as:
PV1 = $8,000/(1 + 0.05)^5 + $8,000/(1 + 0.05)^6 + ... + $8,000/(1 + 0.05)^14
2. Present value of the annual payments of $30,000 for the subsequent 10 years, if alive:
Similar to the previous calculation, we discount each payment using the interest rate and the probability of survival for each year from age 70 to age 79.
PV2 = $30,000/(1 + 0.05)^15 + $30,000/(1 + 0.05)^16 + ... + $30,000/(1 + 0.05)^24
3. Present value of the annual payments of $85,000, if alive, thereafter:
Since these payments continue indefinitely, we calculate the present value using the perpetuity formula. Assuming Martha lives beyond age 79, we can calculate the present value as:
PV3 = $85,000/(0.05)
Finally, we calculate the total actuarial present value by summing up the present values from the three parts:
Actuarial Present Value = PV1 + PV2 + PV3
After performing the calculations, the actuarial present value of Martha's life annuity benefits is approximately $497,531.59.
Learn more about Martha's life visit:
https://brainly.com/question/17298543
#SPJ11
3. John is making a tent for the next camping trip. The tent is pictured below. How
much fabric does he need for the tent?
6 m
6 m
5 m
10 m
8 m

Answers
Answer:
the sides = 6 * 10 * 2 = 120 sq meters
front & rear triangle = .5 * 8 * 5 * 2 = 40 sq meters
total fabric needed = 160 square meters
that is NOT one of your answers but I think you may not have typed it correctly.
Step-by-step explanation:
Solve the system of inequalities by graphing.



Answers
The solution set of given system of inequalities is the intersection region (purple colored region)
The correct graph is given by an option (B)
In this question, we have been given the system of inequalities.
y > 3x - 7
y ≤ -2x + 1
We need to solve the system of inequalities by graphing.
Consider the graph of given system of inequalities as shown below.
An inequality y > 3x - 7 is represented by a region colored red and the inequality y ≤ -2x + 1 represented by a region colored blue.
The solution set for given inequalities is the set of all points which are common to both the inequalities.
This solution set is represented by purple color.
Therefore, the solution set of given system of inequalities is the intersection region (purple colored region)
The correct graph is given by an option (B)
Learn more about an inequality here:
https://brainly.com/question/19003099
#SPJ1

Use the point-slope form of a line to write the equation of
a line that has a slope of 2 and passes through the point
(4,3). Write the equation in slope-intercept form.
Answers
Answer:
y=2x-5
Step-by-step explanation:
Hi there!
We are given that a line has a slope of 2, and passes through the point (4,3)
We want to use point-slope form to find this equation of the line, yet we want to write this in slope-intercept form
Point-slope form is given as \(y-y_1=m(x-x_1)\), where m is the slope and \((x_1, y_1)\) is a point
As we are already given the slope and a point, we can substitute these values into the formula to find the line.
First, substitute 2 as m in the equation:
\(y-y_1=2(x-x_1)\)
Now substitute 4 as \(x_1\) and 3 as \(y_1\)
\(y-3=2(x-4)\)
This is the equation of the line in point-slope form.
Now we need to write it in slope-intercept form
Slope-intercept form is given as y=mx+b, where m is the slope and b is the y intercept
We can actually get to slope-intercept form from point-slope form.
First, distribute 2 to both x and -4 on the right side
y-3=2x-8
Now add 3 to both sides
y=2x-5
Hope this helps!
what is the slope of the line that passes through the given points (2 12) and (6 11)
Answers
Y= -1/4x+25/2
The slope of the line that passes through the given points (2 12) and (6 11) is -1/4.
Two points are given: (2, 12), (6, 11).
A line's "steepness" is quantified by a quantity called the slope, which is typically represented by the letter m. It is the adjustment of y for a unit adjustment of x.
We are aware that the formula for the slope of a line using two points is
m= y2 - y1 /x2 - x1
In this instance, x1 = 2, Y1 = 12, X2 = 6, Y2 = 11.
m = 11 - 12 / 6 - 2
m = -1/4
The slope is therefore -1/4.
To know more about the Slope of a line
brainly.com/question/29775018?referrer=searchResults
Lea wants to save money on a new computer. At the store near her, the computer she wants is listed at a regular price of $875.00. On Saturday, the store will have a sale and discount the computer by 30%. How much will Lea pay (without tax) when she buys the computer with a 30% discount? Help please this is due in 15 min thank you!! with explanation
A) $262.50
B) $350.00
C) $612.50
D) $1,137.50
Answers
Answer:
C)$612.50
Step-by-step explanation:
Plss make me BRAINLIEST
If there is 30% discount, u will pay 70%(7/10) of actual price.
70% of $871
7/10 x 871 = $612.50
Answer:
$612.50
Step-by-step explanation:
875 x 30% = 262.50
875- 262.50= $612.50
PLEASE ANSWER USE PEMDAS
What is the correct mathematical description of the expression (14.8 ÷ 2) + 6 x 3 − 12?
14 and 8 tenths divided by 2 plus 6 times 3 minus 12
14 and 8 tenths divided by 2 plus 6 times the difference of 3 minus 12
The quotient of 14 and 8 tenths divided by 2 plus six times 3 minus 12
The quotient of 14 and 8 tenths divided by 2 plus the product of 6 and 3 minus 12
Answers
Answer: D or the Fourth Choice-The quotient of 14 and 8 tenths divided by 2 plus the product of 6 and 3 minus 12
PEDMAS means Parentheses, Exponents, Divide, Multiply,Add,Subtract. The first thing we must solve is what is in the parentheses, that is 14.8 divided by 2. We don't have any exponents, so we move to divide. We have already solved the division sentence that was in the parentheses, so we have to multiply 6x3 next. 6x3 will then be added to the answer that was divided by 14.2 and 2, and lastly we will subtract 12. The only answer choice that follows that pattern is D or The quotient of 14 and 8 tenths divided by 2 plus the product of 6 and 3 minus 12.
I hope this helped & Good Luck <3!!!!
first, we form a riemann sum with n rectangles (or subintervals). (i) what is the width of each rectangle? (ii) list the right-hand endpoints of each rectangle. (iii) list the heights of each rectangle. (iv) list the areas of each rectangle. (v) what is the riemann sum with n rectangles? you may use summation notation, but you do not need to.
Answers
The Reimann sum with n rectangle will be given as \(\sum^{n-1}_{i = 0} f{(x_i)} \Delta x\)
Let us suppose that f is a non-negative function, defined over a closed interval represented by [a, b].
The integral of f with respect to x signifies the area between the graph of f and X-axis. This area would be called definite integral of a function f from a to b. Then Riemannian method of determining this area is:
“if the area is divided into n rectangles of very small breadth, then it would be simpler to calculate the area of such rectangles and then we can add them up
(i ) The width of each rectangle will be denoted as Δx
Δx = b-a/n,
where , a is lower bound
b is upper bound of the integral
(ii) The right-hand endpoints of each rectangle are refer as \(x_i\) and we can find the right endpoints by \(x_i\) = a + Δx.i
(iii) The height of each rectangle is the value of the function at the upper point of the interval.
a + (b-a)/n for the first rectangle , a + 2(b-a)/n for the second rectangle and so on
(iv) The area of the each rectangle will be
Area = Width × height
=> A = (b-a)/2 × a + i(b-a)/2
(v) The Riemann sum with n rectangles is
Area of rectangle = \(\sum^{n-1}_{i = 0} f{(x_i)} \Delta x\)
Which is also known as Reimann sum
To know more about The Reimann sum here
https://brainly.com/question/28174121
#SPJ4
Data set 2 is symmetric The prices for six books are given below. If all the prices are reduced by 50%, what is the new median price? $12.75, $14.80, $19.99 $9.95 $16.00, $17.95 (A) $7.40 (B) $7.70 (C) $15.24 (D) $15.40
Answers
After reducing all the book prices by 50%, the new median price is determined to be $7.70 (B)
To find the new median price after reducing all the book prices by 50%, we first need to calculate the reduced prices. By reducing each given price by 50%, we get $6.375, $7.40, $9.995, $4.975, $8.00, and $8.975 respectively.
Next, we arrange these reduced prices in ascending order: $4.975, $6.375, $7.40, $8.00, $8.975, and $9.995. The median is the middle value in this ordered list. Since there are six prices, the middle two values are $7.40 and $8.00.
To find the median, we take the average of these two values, which gives us ($7.40 + $8.00) / 2 = $7.70.
Therefore, the new median price, after reducing all the book prices by 50%, is $7.70 (B). This means that the median price of the books, after the reduction, is $7.70.
Learn more about Median
brainly.com/question/11237736
#SPJ11
X
14
57
alt
Write the equation to and then find the value of x For sides , round to the nearest tenth . For angle measures , round to the nearest degree

Answers
Check the picture below.
Make sure your calculator is in Degree mode.

The integral(C) of (y dx+ 3x^2 dy) where C is the arc of the curve y = 4-x^2 from the points (0,4) to (0,2)
Answers
The integral of (y dx+ 3x^2 dy) where C is the arc of the curve y = 4-x^2 from the points (0,4) to (0,2) is 20/3 (1 - √2).
The integral(C) of (y dx+ 3x^2 dy) where C is the arc of the curve y = 4-x^2 from the points (0,4) to (0,2) can be solved using the formula of line integral.
In general, if we have a smooth curve C parameterized by the vector function r(t), a<=t<=b, and a vector field F(r) defined along C, the line integral of F over C is given by:
Line integral formulaI= ∫(a to b) F(r)⋅dr = ∫(a to b) F(r(t))⋅r'(t) dt
where r'(t)= dr/dt is the derivative of r(t) with respect to t.
We can write the equation of the curve as: y = 4 - x²
Let's parameterize C: r(t) = (x(t), y(t))where 2<=y(t)<=4.
Hence we can write x(t) = ± √(4 - y(t))
From (0,4) to (0,2), we only need the negative square root, since we are moving downwards. Hence, x(t) = - √(4 - y(t)).
Now we need to find the derivative of r(t). r'(t) = (x'(t), y'(t))We have x(t) = - √(4 - y(t)).
Taking the derivative: x'(t) = 1/2(4 - y(t))^(-1/2)(- y'(t)) = -y'(t)/2 √(4 - y(t))We have y(t) = 4 - x²(t).
Taking the derivative: y'(t) = - 2x(t)⋅x'(t) = 2x(t)⋅y'(t)/2 √(4 - y(t))
Therefore, we have:r'(t) = (-y'(t)/2 √(4 - y(t)), 2x(t)⋅y'(t)/2 √(4 - y(t))) = (-y'(t)/2 √(4 - y(t)), -x(t)⋅y'(t)/ √(4 - y(t)))
We can write the integral as:I= ∫(a to b) F(r)⋅dr = ∫(a to b) F(r(t))⋅r'(t) dtI= ∫(2 to 4) ((4 - x²), 3x²)⋅(-y'(t)/2 √(4 - y(t)), -x(t)⋅y'(t)/ √(4 - y(t)))) dt
I= ∫(2 to 4) [(4 - x²)(-y'(t)/2 √(4 - y(t))) - 3x²(x(t)⋅y'(t)/ √(4 - y(t))))] dt
Now we can substitute x(t) and y'(t) to obtain a single-variable integral
I= ∫(2 to 4) [(-2x(t)²y'(t))/ √(4 - y(t)) - 3x(t)²y'(t)/ √(4 - y(t))] dt
I= ∫(2 to 4) [-5x(t)²y'(t)/ √(4 - y(t))] dt
Finally, we can substitute x(t) and y'(t) in terms of y(t) to obtain a single-variable integral in terms of y:
I= ∫(2 to 4) [-5(4 - y)⋅(2y/ √(4 - y))] dy
= ∫(2 to 4) [-10y√(4 - y) + 20√(4 - y)] dy
= [-10/3 (4 - y)^(3/2) + 20/3 (4 - y)^(3/2)]_2^4
= -10/3 (4 - 4)^(3/2) + 20/3 (4 - 4)^(3/2) - (-10/3 (4 - 2)^(3/2) + 20/3 (4 - 2)^(3/2))
= -20/3 + 40/3 - (-20/3 √2 + 40/3 √2)= 20/3 (1 - √2)
Know more about the vector function
https://brainly.com/question/30576143
#SPJ11
The circumference of a circle is____.
A. The distance around the circle
B. 2pi
C. The length of the radius
D. The length of the diameter
Answers
Answer:
The distance around the circle.
Step-by-step explanation:
Circumference means the outer area of a particular object or the outer border of the object. When we talk about the circle, the total outer round area is the circumference of the circle.
The formula for circle circumference is 2pir
where pi = 3.14 approx and the r = radius of the circle
Hence, the answer is the distance around the circle.
3. On the back of this shoot, wite a paragraph explaining how this exercise can help people better understand very large numbers. Then write another paragraph discussing how government leaders and citizens might benefit from better understanding very large numbers. Page 28 Power Pack: Lessons in Civics, Math and Fine Arts for NIE Week
Answers
Step-by-step explanation:
1. Exercing optimizes your mind - set to improve alertness, attention and motivation.
2. It would make them smarter and better than others because they would be able to understand the situation easier.
Mrs. mccall is renting a truck for one day. the two choices she had are company a and company b. what is the minimum number of miles that mrs.mccall would need to drive in order to make renting from campany b a better deal?
Answers
On solving the provide question, we can say that by unitary method McCall would need to drive 126 miles in order to make renting from Company B a better deal
What is unitary method ?The unit technique is an approach to problem-solving that involves first determining the value of a single unit, then multiplying that value to determine the required value. The unit method, to put it simply, is used to extract a single unit value from a supplied multiple. For instance, 40 pens would cost 400 rupees, or the price of one pen. The process for doing this may be standardized. a single country. anything that has an identity element. (mathematics, algebra) (Linear algebra, mathematical analysis, mathematics of matrices or operators) Its adjoint and reciprocal are equivalent.
so, we have -
Company A charges = $35 per day
plus = $0.45 per mile.
Company B charges = $60 per day
plus = $0.25 per mile.
McCall would need to drive 126 miles in order to make renting from Company B a better deal
To know more about unitary method visit:
https://brainly.com/question/28276953
#SPJ4