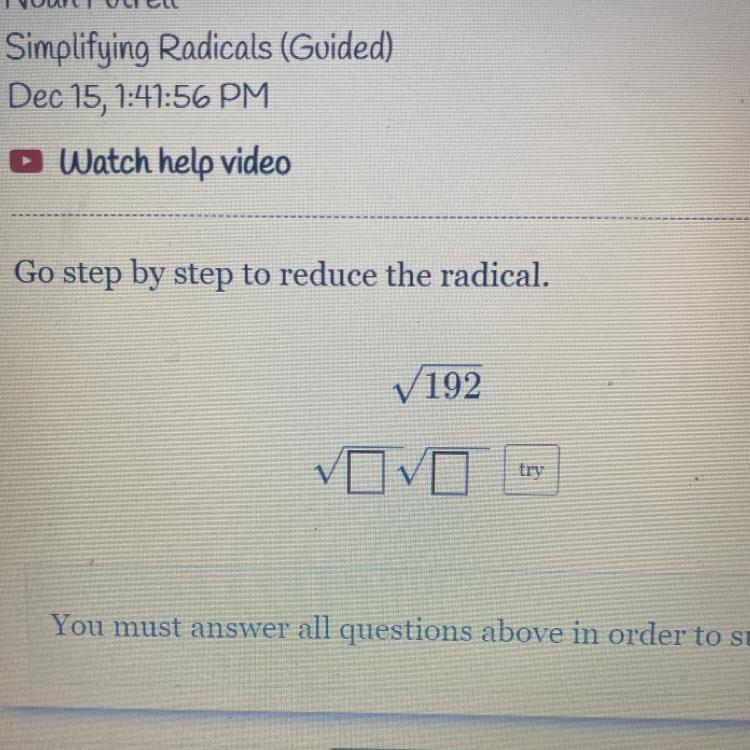
Answers
Answer:
\(3 \sqrt{8} \)
Step-by-step explanation:
1. we are find which factors which when multiplied will give us 192
2. so i took 3 and 64
3. now square root both factors
like this
\( \sqrt{3} \times \sqrt{64} \)
4. then you will be left with 3 and a 8
so then we will write that as the answer given above
Related Questions
Using the convolution theorem, show that L⁻¹ {1 / (s²+b²)² = 1/2b³ (sin bt - bt cos bt)
Hence, solve the differential equation d²y/dt² - 4y = t cos 2t. given that y and dy/dx are both zero when t = 0.
Answers
The solution to the given differential equation is L⁻¹{Y(s)} = (b³ t sin 2t) / (2 (sin bt - bt cos bt))
To solve the differential equation using the convolution theorem, we'll follow these steps:
Take the Laplace transform of both sides of the differential equation.
Use the convolution theorem to simplify the resulting expression.
Take the inverse Laplace transform to obtain the solution in the time domain.
Let's start with step 1:
Given differential equation: d²y/dt² - 4y = t cos 2t
Taking the Laplace transform of both sides, we get:
s²Y(s) - sy(0) - y'(0) - 4Y(s) = L{t cos 2t}
Where Y(s) represents the Laplace transform of y(t), y(0) is the initial condition for y(t) at t = 0, and y'(0) is the initial condition for dy/dt at t = 0.
The Laplace transform of t cos 2t can be found using the Laplace transform table:
L{t cos 2t} = -Im{d/ds[1 / (s² - (2i)²)]}
= -Im{d/ds[1 / (s² + 4)]}
= -Im{(-2s) / [(s² + 4)²]}
= 2Im{(s) / [(s² + 4)²]}
Now let's simplify the expression using the convolution theorem:
The Laplace transform of the convolution of two functions, f(t) and g(t), is given by the product of their individual Laplace transforms:
L{f * g} = F(s) G(s)
In our case, f(t) = y(t) and g(t) = 2Im{(s) / [(s² + 4)²]}.
Therefore, F(s) = Y(s) and G(s) = 2Im{(s) / [(s² + 4)²]}.
Multiplying F(s) and G(s), we get:
Y(s) G(s) = Y(s) 2Im{(s) / [(s² + 4)²]}
Now, we can rewrite the left-hand side of the equation using the convolution theorem:
Y(s) * 2Im{(s) / [(s² + 4)²]} = L{t cos 2t}
Taking the inverse Laplace transform of both sides, we have:
L⁻¹{Y(s) * 2Im{(s) / [(s² + 4)²]}} = L⁻¹{L{t cos 2t}}
Simplifying the right-hand side using the inverse Laplace transform table, we get:
L⁻¹{Y(s) * 2Im{(s) / [(s² + 4)²]}} = t sin 2t / 4
Now, we can apply the convolution theorem to the left-hand side of the equation:
L⁻¹{Y(s) * 2Im{(s) / [(s² + 4)²]}} = L⁻¹{Y(s)} * L⁻¹{2Im{(s) / [(s² + 4)²]}}
The inverse Laplace transform of 2Im{(s) / [(s² + 4)²]} can be found using the inverse Laplace transform table:
L⁻¹{2Im{(s) / [(s² + 4)²]}} = 1 / 2b³ (sin bt - bt cos bt)
Therefore, we have:
L⁻¹{Y(s)} * 1 / 2b³ (sin bt - bt cos bt) = t sin 2t / 4
From this, we can deduce the inverse Laplace transform of Y(s):
L⁻¹{Y(s)} = (t sin 2t / 4) / (1 / 2b³ (sin bt - bt cos bt))
Simplifying further:
L⁻¹{Y(s)} = (b³ t sin 2t) / (2 (sin bt - bt cos bt))
This is the solution to the given differential equation.
Know more about Convolution theorem here:
brainly.com/question/32608612
#SPJ11
Addison invested $440 in an account paying an interest rate of 2%
compounded continuously. Assuming no deposits or withdrawals are
made, how long would it take, to the nearest tenth of a year, for the
value of the account to reach $610?
Answers
Answer:
16.3
Step-by-step explanation:
Continuously compounding interest formula:
pe^(r*t)
we know that
440e^(.02x)=610
Sovle for x
e^.02x=1.38
.02x=ln1.38
.02x=.3267
x=16.3
Answer:
16.3
Step-by-step explanation:
I got it right
during the 2000 season, the home team won 138 of the 240 regular season national football league games. is this strong evidence of a home field advantage in professional football? test an appropriate hypothesis and state your conclusion. be sure the appropriate assumptions and conditions are satisfied before you proceed.
Answers
A) The 95% confidence interval is:
0.58 ± 0.062
B) At the 0.01 probability value, there is neither substantial evidence of a home-field advantage in professional football (they won and over half of the games).
Now, According to the question:
A) Confidence interval is written as
Sample proportion ± margin of error
Margin of error = z × \(\frac{\sqrt{pq} }{n}\)
Where:
z = The z score corresponds to the amount of confidence.
p = sample proportion.
q = probability of failure
q = 1 - p
p = x/n
Where
n = the number of samples
x = the number of success
From the information given,
n = 240
x = 138
p = 138/240 = 0.58
q = 1 - 0.58 = 0.42
To determine the z score, The confidence level from 100% to get α
α = 1 - 0.95 = 0.05
α/2 = 0.05/2 = 0.025
Thus,
1 - 0.025 = 0.975
The z -score associated with the area just on z table approximately 1.96. Therefore, the z score with a 95% confidence level is 1.96.
As a result, the 95% confidence interval becomes
0.58 ± 1.96√(0.58)(0.42)/240
Confidence interval is
0.58 ± 0.062
B) Earning more than half of the games equates to winning 120 games or more.
p = 120/240 = 0.5
The hypothesis test will be
For the null hypothesis,
P ≥ 0.5
For the alternative hypothesis,
P < 0.5
Probability of success, p = 0.5
q = probability of failure = 1 - p
q = 1 - 0.5 = 0.5
Considering the sample,
Sample proportion, P = x/n
Where
x = number of success = 138
n = number of samples = 240
P = 138/240 = 0.58
We need to find the values of the test statistic which will be the z score
z = (P - p)/√pq/n
z = (0.58 - 0.5)/√(0.5 × 0.5)/240 = 2.48
Remember that this is a two-tailed test. We would use the normal distribution table to calculate the probability potential of the property to the right of both the z score.
P value will be = 1 - 0.9934 = 0.0066
Since alpha, 0.01 > the p value, 0.0066, then we would reject the null hypothesis.
The given question is incomplete, The complete question is this:
__"During the 2000 season, the home team won 138 out of 240 regular season National Football League games. (15 points) a) Construct a 95% confidence interval for the winning proportion of the home team during this season. b) At the 0.01 significance level, is there strong evidence of a home field advantage (they win more than half of the games) in professional football? State hypotheses, calculate the test statistic and p-value, and make a conclusion in context"__
Learn more about Confidence Interval at:
https://brainly.com/question/29680703
#SPJ4
a) Use the Fisher information contained in a sample of size n to find the variance of the sample mean for the Poisson distribution.
b) Let X1, X2,..., X, denote a random sample from the Bernoulli population. Show that
the
Var Oln f(x; e) дв = E Olnf( дв
(c) Let X1, X2,..., X, be a random sample from a normal population with mean and variance 1, and (0) = 0².
Use the Cramer-Rao Lower Bound to find the minimum variance of any estimator
of (0) and comment on its value.
(11)
Answers
The variance of the sample mean for the Poisson distribution can be determined using the Fisher information contained in a sample of size n.
How can the variance of the sample mean for the Poisson distribution be derived using the Fisher information?The Fisher information, denoted as I(λ), for the Poisson distribution with parameter λ is equal to 1/λ. Since the sample mean is an unbiased estimator of λ, its variance can be obtained using the Cramer-Rao Lower Bound (CRLB), which states that the variance of any unbiased estimator is greater than or equal to 1/n times the reciprocal of the Fisher information.
Learn more about the Poisson distribution
brainly.com/question/30388228
#SPJ11
If the diagonal of the rectangle is 10.5 inches and the length of the rectangle is 7.25, what is the width of the rectangle?
Answers
Answer:
w≈7.6in
Step-by-step explanation:
L= 7.25
D= 10.5
Using the formula \(d=\sqrt{w^{2} + l^{2} } \\\)Solving for w \(w=\sqrt{d^{2} -l^{2} }\) \(\sqrt{10.52^{2}-7.25^{2} } = 7.59523in\)Answer:-
The width of this rectangle is = 7.59
Given:-
In this question, it is given that -
The diagonal of this rectangle is = 10.5
the length of this rectangle is = 7.25
To find:-
We have to find the width of this rectangle.
Solution:-
We can easily solve this problem using the Pythagorean theorem.
In this problem, it is given that the length of this rectangle is = 7.25 and the diagonal is =10.5
so by the Pythagorean theorem, we can get-
(length)² + (width)² = (diagonal)²
or, (7.25)² + (width)² = (10.5)²
or, (width)² = (10.5)² - (7.25)²
= 17.75 × 3.25
= 57.6875
or, width = 7.59
So, the width of the rectangle is 7.59.
What is the slope of y=x+5?
Answers
Answer:
1
Step-by-step explanation:
since the formula is
y=x+5 and x is the slope
1 is the slope
Answer:
the slope is 1 and the y intercept is 5
What is significance of knowing the linear and non-linear portion of a standard curve? a.readings within the non-linear portion can be used for determination of protein absorbance b.within the non-linear portion can be used for determination of protein concentration c.readings within the linear portion can be used for determination of protein absorbance d.readings within the linear portion can be used for determination of protein concentration
Answers
The significance of knowing the linear and non-linear portion of a standard curve is that it helps in determining the accuracy and reliability of the measurements taken. The answer in option d.
The significance of knowing the linear and non-linear portions of a standard curve lies in accurate determination of protein concentrations. Readings within the linear portion of the curve allow for a reliable calculation of protein concentrations, as there is a consistent relationship between absorbance and concentration. In contrast, readings within the non-linear portion are less reliable for determining protein concentrations due to the inconsistent relationship between absorbance and concentration. Therefore, the correct answer is: d. readings within the linear portion can be used for determination of protein concentration.
To learn more about determination of protein concentrations click here: brainly.com/question/29459537
#SPJ11
3. The area of quadrilateral ABCD is 12 sq. units. Find X.
Answers
x is 9
Okay bye bye
:9 :O)
what is 200 c in fahrenheit?
Answers
Answer:
392
Step-by-step explanation:
To convert temperatures in degrees Celsius to Fahrenheit, multiply by 1.8 (or 9/5) and add 32.
On converting 200° Celsius to Fahrenheit the value is obtained as 392° F.
What is temperature?
The average kinetic energy of the particles in an object is measured by its temperature. The velocity of these particles likewise increases as the temperature rises.
A thermometer or a calorimeter is used to determine the temperature. In other words, a system's internal energy is determined by its temperature.
According to the International System of Units, Kelvin, denoted by the letter K, is the SI unit of temperature. In the fields of science and engineering, the Kelvin scale is commonly acknowledged or utilised. However, the Celsius or Fahrenheit scale is used to measure temperature throughout the majority of the world.
The formula for converting Celsius to Fahrenheit is -
F = (C × 9/5) + 32
The temperature in Celsius is given as - 200° Celsius
Substitute the values in the equation -
F = (200 × 9/5) + 32
F = (40 × 9) + 32
F = 360 + 32
F = 392° F
Therefore, the temperature in Fahrenheit is 392° F.
To learn more about temperature from the given link
https://brainly.com/question/25677592
#SPJ4
Which function has a domain of all real numbers?
A. y=-x½+5 B. y=(2x)⅓-7 C. y=(x+2)¼ D. y=-2(3x)⅙?
Answers
Answer:
B.
Step-by-step explanation:
B. Because the others have exponents whose denominators are even so the results of , for example x^1/2, if x is negative is not defined.
For example:
For A, when x is -4, (-4)^1/2 is not real.
For B, when x = -4, (2*-4)^ 1/3 = -8^(1/3) = = -2.
Answer:
Step-by-step explanation:
For all Plato users

samia needs to subtract 37 from 54 she cant subtract 7 from 4 so she subtracts 4 from 7 will she get the right answer? Explain how you know
Answers
solve ALL please . work needed
5x-1=x+115
3+5q=9+4q
2b+4=-18-9b
Answers
5x-x=115+1
4x=116
x=116/4
x=29 (Answer)
2) 3+5q=9+4q
5q-4q=9-3
q=6 (Answer)
3) 2b+4=-18-9b
2b+9b=-18-4
11b=-22
b=-22/11
b=-2 (Answer)
Hope this helps
find the median of the data set of 17,35,20,18,29,26
Answers
The median to this problem is 23
read the picture plsssssssssssss

Answers
If the expression be 23 x² + 3x + 8 then the constant exists 8.
What is meant by expression?The addition, subtraction, multiplication, and division arithmetic operators are used to write a group of numbers together to form a numerical statement in mathematics. The expression of a number can take on various forms, including verbal form and numerical form.
A mathematical expression is a finite combination of symbols that is well-formed in accordance with context-specific norms.
A mathematical expression is a phrase that includes at least two numbers or variables, at least one arithmetic operation, and the expression itself. Any one of the following mathematical operations can be used. A sentence has the following structure: Number/variable, Math Operator, Number/Variable is an expression.
During the course of a program's execution, a constant's value cannot change. As a result, the value is constant, as implied by its name. During the course of a program's execution, a variable's value can change. As a result, the value might change, as implied by its name.
Let the expression be 23 x² + 3x + 8
then the constant exists 8.
Therefore, the correct answer is option C. 8.
To learn more about expression refer to:
https://brainly.com/question/723406
#SPJ1
find the missing value and please show how

Answers
Answer:
x=10 degrees.
Step-by-step explanation:
(6x-5)+5x+75=180
180 from the measure of degrees in a triangle*
Solve this equation.
11x+70=180
11x=110
x=10
x=10 degrees.
What is the area of this figure

Answers
Answer:
108
Step-by-step explanation:
add all of the numbers together and thats what you get :)
please help it’s on of my last questions
Determine whether you can construct many, one, or no triangle(s) with each description.

Answers
Many
One
I’m pretty sure.
A tortoise walks 52.0 feet per hour. Convert this speed into inches per minute.
Answers
Answer:
10.4 inches per minute
Step-by-step explanation:
52 ft -> 60 mins
624 in -> 60 mins
10.4 -> 1 min
Hello User,
Answer:
10.4 in per min
Step-by-step explanation:
First multiply 52 by 12 to get inches per hour. 624 in per hour. Then make it 624 inches in 60 minutes. Divide 624 by 60 to get 10.4. So it's speed in inches per minute is 10.4 in per min.
am i just supposed to multiply? it’s due today can someone please answer

Answers
Answer:
103 km2
Step-by-step explanation:
hope it helps :)
Answer:
A. 51.5 km²
Step-by-step explanation:
Area of parallelogram = b x h
= 10.3 x 5
= 51.5
Layla has 12 forks and 18 knives to place in cutlery holders at the fast food restaurant where she works. She wants to distribute them equally, with no forks or knives left over. What is the greatest number of cutlery holders Layla can stock
Answers
Answer:
The greatest number of cutlery holders Layla can stock is 15 holders.
Step-by-step explanation:
You can put 2 of each type of cutlery in each holder.
12 forks use 6 holders.
18 knives use 9 holders.
6+9=15
The greatest number of cutlery holders Layla can stock is 15 holders.
2) The representative agent lives for infinite periods (0,1,2,…) and receives exogenous incomes of y0,y1,y2,…, respectively. The lifetime present discounted value of utility is given by: ∑t=0[infinity]βtln(ct) with β(<1) being the discount factor and ct is consumption at time t. The agent is allowed to save or borrow at the real interest rate r, but she cannot die with debt or wealth. Assume also that the initial wealth is zero. a. Solve the optimization problem of the agent using the period-by-period budget constraints. In particular, show the Euler equation. b. Using the given functional form, write the Euler equation between time 1 and time 3 . In other words, show how c1 and c3 are related. c. Write the present discounted value of optimal lifetime consumption as a function of c0 (and, potentially, other parameters or exogenous variables). d. Write the present discounted value of optimal lifetime utility as a function of c0 (and, potentially, other parameters or exogenous variables). e. Find the present discounted value of lifetime income as a function of y0 (and, potentially, other parameters or exogenous variables) when income is growing each period at the rate of γ, where 0<γ0 ? Explain!
Answers
a. U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. U0 = ∑t=0[infinity](β(1 + r))^tln(ct). This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income.
a. The optimization problem of the representative agent involves maximizing the present discounted value of utility subject to the period-by-period budget constraint. The Euler equation is derived as follows:
At each period t, the agent maximizes the utility function U(ct) = ln(ct) subject to the budget constraint ct = (1 + r)wt + yt, where wt is the agent's wealth at time t. Taking the derivative of U(ct) with respect to ct and applying the chain rule, we obtain: U'(ct) = β(1 + r)U'(ct+1). This equation is known as the Euler equation, which represents the intertemporal marginal rate of substitution between consumption at time t and consumption at time t+1.
b. The Euler equation between time 1 and time 3 can be written as U'(c1) = β(1 + r)U'(c2), where c1 and c2 represent consumption at time 1 and time 2, respectively.
Similarly, we can write the Euler equation between time 2 and time 3 as U'(c2) = β(1 + r)U'(c3). Combining these two equations, we fin
d U'(c1) = β(1 + r)^2U'(c3). This relationship shows that the marginal utility of consumption at time 1 is equal to the discounted marginal utility of consumption at time 3.
c. The present discounted value of optimal lifetime consumption can be written as C0 = ∑t=0[infinity](β(1 + r))^tct. This equation represents the sum of the discounted values of consumption at each period, where the discount factor β(1 + r) accounts for the diminishing value of future consumption.
d. The present discounted value of optimal lifetime utility can be written as U0 = ∑t=0[infinity](β(1 + r))^tln(ct).
This equation represents the sum of the discounted values of utility at each period, where the discount factor β(1 + r) reflects the time preference and the logarithmic utility function captures the agent's preference for consumption.
e. The present discounted value of lifetime income, denoted as Y0, can be expressed as Y0 = y0 + (1 + γ)y1 + (1 + γ)^2y2 + ..., where γ represents the growth rate of income. The income in each period is multiplied by (1 + γ) to account for the increasing income over time.
This assumption of income growth allows for a more realistic representation of the agent's economic environment, where income tends to increase over time due to factors such as productivity growth or wage increases.
for such more questions on equation
https://brainly.com/question/17145398
#SPJ8
Find the value of x to the nearest tenth.

Answers
Answer:
4.5
Step-by-step explanation:
a^2+b^2=c^2
64+16=80=c^2
c=80^0.5
x^2+80=100
x^2=20
x=4.5
Which of the following is true?
A. Segment RS is an altitude of triangle TRS
B. Segment QR is an altitude of triangle QRT
C. Segment QS is an altitude of triangle QRS
D. Segment RT is an altitude of triangle QRS

Answers
The correct statement is D. Segment RT is an altitude of triangle QRS
What is the altitude of right triangle?Altitude in a right triangle refers to the line segment drawn from the right angle of the triangle to the opposite side, forming a perpendicular line.
The length of this altitude is also known as the height of the triangle.
The altitude of a right triangle can be calculated using the Pythagorean theorem or trigonometric functions, depending on the information given.
Learn more about right triangle at:
https://brainly.com/question/2437195
#SPJ1
What is the equation of the line that passes through the point (3, -5) and has a
slope of 2/3?
Answers
who proposed that a punched card be used for counting the census?
Answers
Herman Hollerith proposed the use of punched cards for counting the census.
The punched card system for counting the census was proposed by Herman Hollerith. Hollerith was an American inventor and statistician who developed the punched card tabulating machine. He presented his idea in the late 19th century as a solution to the challenge of processing and analyzing large amounts of data efficiently.
Hollerith's system involved encoding information on individual cards using punched holes to represent different data points. These cards were then processed by machines that could read and interpret the holes, enabling the automatic counting and sorting of data. The punched card system revolutionized data processing, making it faster and more accurate than manual methods.
Hollerith's invention laid the foundation for modern computer data processing techniques and was widely adopted, particularly by government agencies for tasks like the census. His company eventually became part of IBM, which continued to develop and refine punched card technology.
In summary, Herman Hollerith proposed the use of punched cards for counting the census. His invention revolutionized data processing and laid the groundwork for modern computer systems.
Know more about census here,
https://brainly.com/question/32843211
#SPJ11
answer and work please

Answers
Let the graph of g be a vertical stretch by a factor of 2 and a
reflection in the x-axis, followed by a translation 3 units down of
the graph of f(x) = x². Write a rule for function g and identify the
vertex.

Answers
Vertex is slang for a corner or a place where two lines converge.The four corners of a square, for instance, are each referred to as a vertex.
Write a rule for function g and identify the vertex ?
The graph of g is a vertical stretch by a factor of 2 followed by a translation of 3 units down of the graph of f(x) = (x-1)²then the function g(x) = 2(x+4)²
f(x) =x²-2x+1 The graph of g be a vertical stretch by a factor of 3 and a reflection in the y-axis, followed by a translation 2 units left of the graph of .f(x) =x²-2x+1
Rewrite the given function f(x).
f(x) = (x-1)²
Now, the graph is stretched vertically by a factor of 2.
= 2(-x-1)²
reflect the graph about the y-axis.
2(x+1)²
move to the left by 3 units.
= 2(x+3+1)²
=2(x+4)²
The function g(x) =2(x+4)²
To learn more about vertex function refer
https://brainly.com/question/18102238
#SPJ13
A ball shaped like a sphere has a radius of 5.4 centimeters. Which measurement is closest to the volume of the ball in cubic centimeters?
Answers
Answer:
Step-by-step explanation:
volume of sphere = 4πr³/3 = 4π5.4³/3 ≈ 660 cm³
The volume of the given spherical ball is 660 cm³
What is sphere?A sphere is a geometrical object that is a three-dimensional analogue to a two-dimensional circle. A sphere is the set of points that are all at the same distance r from a given point in three-dimensional space.
Given that, A ball-shaped like a sphere has a radius of 5.4 centimetres.
Volume of the sphere = 4/3 π × radius³
= 4/3 × 3.14 × (5.4)³
= 659.24 ≈ 660
Hence, the volume of the given spherical ball is 660 cm³
For more references on sphere, click;
https://brainly.com/question/29632303
#SPJ6
1. If f(x) = (3x-2)/(2x+3), then f'(x) =
Answers
Answer:
\(f'(x)= \frac{13}{(2x+3)^2}\\\)
Step-by-step explanation:
\(f(x)= \frac{3x-2}{2x+3} \\\)
\(f'(x)=\frac{dy}{dx} = \frac{d}{dx}(\frac{3x-2}{2x+3})\\ f'(x)= \frac{(2x+3)\frac{d}{dx}(3x-2)-(3x-2)\frac{d}{dx}(2x+3) }{(2x+3)^{2} } \\f'(x)= \frac{(2x+3)(3)-(3x-2)(2)}{(2x+3)^{2} } \\\)
\(f'(x)= \frac{6x+9-6x+4}{(2x+3)^{2} }\\ f'(x)= \frac{13}{(2x+3)^2}\\\)
PLEASE URGENT HELP!!!!!!!
Gerald assembled a wooden gate, as shown below, where each of the six boards that make up the lower part of the gate are the same size and the top piece is a semi-circle shaped piece of wood.
If x = 6 inches, y = 2 inches, and z = 3 feet, what is the volume of wood used to make the gate, to the nearest cubic inch?
A. 2,746 in3
B. 1,234 in3
C. 4,628 in3
D. 3,610 in3

Answers
Answer:
Maybe 2 or 3
Step-by-step explanation: