GIVING BRAINLIST!!! m∠GHI=98° and m∠JKL=82°.
Which statement is true about ∠GHIand∠JKL?
The angles are neither complementary nor supplementary.
The angles are complementary.
The angles are supplementary.
Answers
Answer:
The angles are supplementary
Step-by-step explanation:
Complementary angles amount to 90 degrees when added together.
Supplementary angles amount to 180 when added together.
82 + 98 = 180
So This set of angles is supplementary
Related Questions
HELP ASAP!
The graphs below have the same shape. f(x) = x2.
What is the equation of the graph of g(x)?

Answers
Answer:
A
Step-by-step explanation:
Given the graph of f(x) then f(x + a) is a horizontal translation of f(x)
• If a > 0 then a shift to the left of a units
• If a < 0 then a shift to the right of a units
Here g(x) is the graph of f(x) shifted 3 units to the left, then
g(x) = (x + 3)² → A
Answer:
A
Step-by-step explanation:
pleaseeee explain !!!

Answers
A is the answer because if we want the unit rate we do
2/3÷2/3 and 15 1/5, we can turn 15 1/5 into a improper fraction first so 76/5 and we do 76/5 ÷2/3 which is equal to
76/5×3/2=114/5
114/5 simplifies into 24 4/5.
so Naomi can travel 24 4/5 gal per mile.
Hope this helps!
Acellus
Find the area of the following
parallelogram:
1.5 cm
2.5 cm
2.25 cm
A= [?] cm?
Enter the exact answer as a decimal.
Enter
Answers
Answer:
Question:Find the area of the following
parallelogram:
1.5 cm
2.25 cm
Solution:\( \huge\fbox\purple{Area = Product of the given 2 sides}\ \)
(1.5×2.25)cm²= 3.375 cm²Hope it helps
-------☆゚.・。゚ᵴɒƙυᴚᴀ_ƨȶäᴎ❀
Step-by-step explanation:
\(3.375 \: {cm}^{2} \)
I hope it helps
have a great day
#Captainpower
Which angle is formed by EA−→
and EG−→−?
Select all that apply.

Answers
Answer:
Step-by-step explanation:
\(\angle 2,\angle AEG, \angle GEB\)
a helicopter lifts a 65 kg astronaut 15 m vertically from the ocean by means of a cable. the acceleration of the astronaut is g/12. how much work is done on the astronaut by a) the force from the helicopter
Answers
The work done on the astronaut by the force from the helicopter is \(W_h=10,351.25J\)
We have the following information from the question is:
Mass of the astronauts , m = 65 kg
Vertical distance is, d = 15m .
Acceleration of the astronaut is, a = g/12
The forces in the vertical directions are balanced as,
F - mg = ma
F = m(a + g)
F = m(g/12 + g)
F = 13/12mg
Now, work done on the astronaut by the helicopter can be calculated as,
W= Fd .....(1)
Substitute the values in the above expression, and we get,
\(W_h=\frac{13}{12} mgd\)
\(W_h=\frac{13}{12}(65)(9.8)(15)\)
\(W_h=10,351.25\)
Learn more about Work and force at:
https://brainly.com/question/4095205
#SPJ4
Need Help ASAP
Can someone help me with this problem

Answers
Answer:
Hopes it helps
Step-by-step explanation:
Len
Simplifying
5(3 + -8x) = 0
(3 * 5 + -8x * 5) = 0
(15 + -40x) = 0
Solving
15 + -40x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-15' to each side of the equation.
15 + -15 + -40x = 0 + -15
Combine like terms: 15 + -15 = 0
0 + -40x = 0 + -15
-40x = 0 + -15
Combine like terms: 0 + -15 = -15
-40x = -15
Divide each side by '-40'.
x = 0.375
Simplifying
x = 0.375
Monty
Simplifying
7 + -2(-5x) = 0
Remove parenthesis around (-5x)
7 + -2 * -5x = 0
Multiply -2 * -5
7 + 10x = 0
Solving
7 + 10x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-7' to each side of the equation.
7 + -7 + 10x = 0 + -7
Combine like terms: 7 + -7 = 0
0 + 10x = 0 + -7
10x = 0 + -7
Combine like terms: 0 + -7 = -7
10x = -7
Divide each side by '10'.
x = -0.7
Simplifying
x = -0.7
Nailany
Simplifying
7 + -6 + -16x = 0
Combine like terms: 7 + -6 = 1
1 + -16x = 0
Solving
1 + -16x = 0
Solving for variable 'x'.
Move all terms containing x to the left, all other terms to the right.
Add '-1' to each side of the equation.
1 + -1 + -16x = 0 + -1
Combine like terms: 1 + -1 = 0
0 + -16x = 0 + -1
-16x = 0 + -1
Combine like terms: 0 + -1 = -1
-16x = -1
Divide each side by '-16'.
x = 0.0625
Simplifying
x = 0.0625
David wants to buy a new tablet computer. He looks at a sales ad and sees that a computer store is selling a tablet computer for $499 which is 1/3 off the regular price.
Part A:
Write an equation that represents the situation. Let x = the original cost of the tablet.
Part B:
Find the original cost of the tablet computer.
Answers
Answer:
Part A: x÷3=$499
Part B: $1497
Step-by-step explanation:
A: Because to find a fraction of somthing we have to divide, so in this case we divided the original price by 3 to get $499.
B:To find the original price we have to multiply the one third of it ($499) by 3 to get the original amount.
Goode Manufacturing pays Betty Robert's a $1770 monthly salary plus a 14% commission on merchandise she sells each month. assume Betty's sales were $99,200 for last month. calculate the following amounts: 1.amount of commission? gross pay?
Answers
Given:
Betty's monthly salary = $1770
Commision on sales = 14%
Betty sales for last month = $99,200
1. The amount of commission is 14% of $99,200.
Therefore, we have:
\(\frac{14}{100}\times99200=0.14\times99200=\text{ \$13888}\)The amount of commission is $13,888
2. The gross pay.
Gross pay is the amount Betty receives before taxes and deductions.
Gross pay = Salary + Commission
Thus, the gross pay is:
$13888 + $1770 = $15,658
ANSWER:
1. Commission = $13,888
2. Gross pay = $15,658
For a specific species of fish in a pond, a wildlife biologist wants to build a regression equation to predict the weight of a fish based on its length. The biologist collects a random sample of this species of fish and finds that the lengths vary from 0.75 to 1.35 inches. The biologist uses the data from the sample to create a single linear regression model. Would it be appropriate to use this model to predict the weight of a fish of this species that is 3 inches long?
a. Yes, because 3 inches falls above the maximum value of lengths in the sample.
b. Yes, because the regression equation is based on a random sample.
c. Yes, because the association between length and weight is positive.
d. No, because 3 inches falls above the maximum value of lengths in the sample.
e. No, because there may not be any 3-inch fish of this species in the pond.
Answers
The correct answer is: d. No, because 3 inches falls above the maximum value of lengths in the sample.
In linear regression, the model is based on the relationship observed in the sample data. The biologist collected data on fish lengths ranging from 0.75 to 1.35 inches, so the model is only valid within that range. Extrapolating the model to predict the weight of a fish with a length of 3 inches would be beyond the observed range of the data. This can lead to unreliable predictions as the relationship between length and weight may not hold true for lengths beyond the range of the sample.
To know more about linear regression, visit:
https://brainly.com/question/32840471
#SPJ11
SOMEBODY PLEASE HELP ASAP!!! WILL GIVE BRAINLIEST
In parallelogram KLMN, KN = 10, MN = 7 and mK = 50°
Find the measures of the remaining angles of parallelogram KLMN. Justify each of the measures with a theorem.
Find the measures of the remaining side lengths of parallelogram KLMN. Justify each of the measures with a theorem.

Answers
Answer:
a- 130, 130, and 50
b- 7 and 10
Answer:
a- 130, 130, and 50
b- 7 and 10
Step-by-step explanation:
7+ -(8) - 1= what is the answer
Answers
Answer: -2
Step-by-step explanation:
Answer:
-2
Step-by-step explanation:
7+(-8)-1
change to: 7-8-1
combine like terms (-8 and -1)
7-9
= -2
the american management association is studying the income of store managers in the retail industry. a random sample of 49 managers reveals a sample mean of $45,420. the standard deviation of the population is $2,050. using a 95% level of confidence, what is the confidence interval for the population mean?
Answers
Answer:
burgers
Step-by-step explanation:
ahhhhhhhhhhhhhhhhhh
need help please
find the area of the shape below
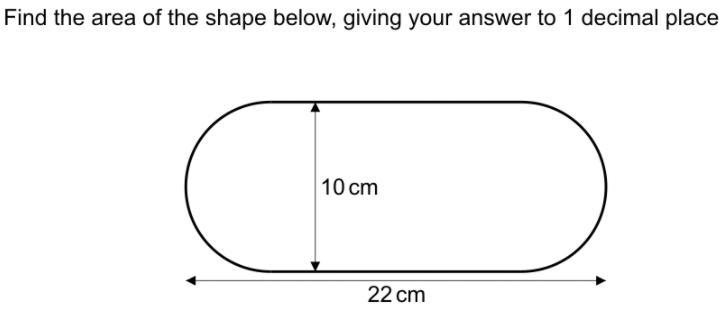
Answers
Answer:
\(198.5\ cm^2\)
Step-by-step explanation:
Break the figure in three parts as shown in the image I attached.
The figure makes 2 semi circles and 1 rectangle so,
Area of rectangle = Length x breadth
Area of rectangle = 12 x 10
Area of rectangle = 120
Now for the semi circles , we have 2 semi-circles which means area of both semi circles would be
Area of semi circle = \(\frac{1}{2} \pi r^2\\\)
so, Area of two semi circles would be = \((\frac{1}{2} \pi r^2)2\)
so, Area of two semi circles would be = \(\pi r^2\)
now for the radius we know that,
Diameter = 2 x radius
D = 2r
and the diameter is 10cm so,
10 = 2r
10/2 = r
r = 5cm
so we put r = 5 in the formula ,
\(Area\ of\ two\ semi\ circles\ = \pi r^2\\Area\ of\ two\ semi\ circles\ =\pi (5)^2\\Area\ of\ two\ semi\ circles\ =25\pi \\Area\ of\ two\ semi\ circles\ =78.5\ cm^2\)
So now the total area of the figure is
Total Area = Area of rectangle + Area of two semi circles
Total Area = 120 + 78.5
Total Area = 198.5 cm^2
In an election, Candidate A received 75 votes and candidate B received 25 votes, after the first 100 votes were counted. Assume this ratio is maintained. If Candidate B received 750 votes, how many votes did Candidate A receive?
Answers
Step-by-step explanation:
In an election, Candidate A received 75 votes and candidate B received 25 votes, after the first 100 votes were counted. Assume this ratio is maintained. If Candidate B received 750 votes, how many votes did Candidate A receive?
If QSR=YXZ describes two triangles, which other statement is also true?

Answers
The statement that is also true to ΔQSR ≅ ΔYXZ is ΔQRS ≅ ΔYZX.
How to find congruent triangle?Two triangles are defined to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. In other words, triangles are congruent when they have exactly the same three sides and exactly the same three angles.
Therefore,
ΔQSR ≅ ΔYXZ
Therefore, another statement that is equal to the congruency of the triangle is as follows:
ΔQRS ≅ ΔYZX
learn more on congruent triangle here: https://brainly.com/question/4132028
#SPJ1
Use a Lagrange multiplier to find the maximum and minimum values of the function f(x,y,z) = 5x^2 * y + 4z. considering only values of x, y, and z that satisfy the equations x^2+y^2=9 and z=3y.
Answers
The maximum and minimum of Lagrange can be 1/2,1/2.
The maximum and minimum of Lagrange can be found in what way?The equation of indexes between three G subgroups is a case where Lagrange's theorem can be applied. Since e is G's identity element, if we assume K = e, [G: e] = |G| and [H: e] = |H|. The original equation |G| = [G: H] |H| can thus be found.The equation of indexes between three G subgroups is a case where Lagrange's theorem can be applied. Since e is G's identity element, if we assume K = e, [G: e] = |G| and [H: e] = |H|. The original equation |G| = [G: H] |H| can thus be found.Explanation:
Maximum value = (1/2,1/2).
Minimum value = (1/2,1/2).
To learn more about Lagrange's theorem refer to:
https://brainly.com/question/29658907
#SPJ1
The maximum and minimum of Lagrange can be 1/2,1/2.
The maximum and minimum of Lagrange can be found in what way?The equation of indexes between three G subgroups is a case where Lagrange's theorem can be applied. Since e is G's identity element, if we assume K = e, [G: e] = |G| and [H: e] = |H|. The original equation |G| = [G: H] |H| can thus be found.
The equation of indexes between three G subgroups is a case where Lagrange's theorem can be applied. Since e is G's identity element, if we assume K = e, [G: e] = |G| and [H: e] = |H|. The original equation |G| = [G: H] |H| can thus be found.
Explanation:
Maximum value = (1/2,1/2).
Minimum value = (1/2,1/2).
To learn more about Lagrange's theorem refer to:
brainly.com/question/29658907
#SPJ1
Solve (y/4) +3 = 7
a) y = 40
b) y = 1
c)y = 25
d) y = 16
Answers
(Y/4) +3 = 7
Subtract 3 from both sides:
Y/4 = 4
Multiply both sides by 4
Y = 16
Answer:
Option D
Step-by-step explanation:
=> (y/4)+3 = 7
Subtracting 3 from both sides
=> y/4 = 7-3
=> y/4 = 4
Multiplying 4 to both sides
=> y = 4*4
=> y = 16
What is the MEAN of the data set below?(0.2,0.8,0.4,0.3,0.4,0.4,0.4,0.8,1.3)
Answers
Answer:
5/9
Step-by-step explanation:
we add all of the values and divide by the total number in this case 9, all of them add to make 5 so we do 5÷9 to get 5/9
what is the greatest common factor of 3 and 21x?
Answers
Answer:
3
Step-by-step explanation:
3 ÷ 3 = 1
21x ÷ 3 = 7x
There is no other common factor.
at the same temperature and pressure, balloons of equal volume always contain_____
Answers
At the same temperature and pressure, balloons of equal volume will always contain the same amount of air molecules due to the constant collisions of the molecules with each other and the walls of the container.
At the same temperature and pressure, balloons of equal volume will always contain the same amount of air molecules. This is because air molecules take up a certain amount of space, and the same amount of air molecules will take up the same amount of space regardless of the container. The molecules are constantly colliding with each other and the walls of the container, pushing against the walls and applying a pressure to the walls of the container. Since the pressure is the same, the amount of air molecules will remain the same and thus the volume of air in the container will remain the same. In this case, since the balloons are of equal volume, they will both contain the same amount of air molecules.
Learn more about temperature here
https://brainly.com/question/29768169
#SPJ4
A parallelogram has a base of 20 millimeters and a height that is 6 mm less than the base. Create an equation that
can be used to find the area, A, of the parallelogram in square millimeters.
Move the correct answer to each box. Not all answers will be used.

Answers
Which of the following pair of triangles demonstrates that two triangles with three congruent angles are not necessarily congruent?




Answers
Answer:
it is A.
Step-by-step explanation:
this should be A.
if it isn't sorry

Answer:
A.
Step-by-step explanation:
what is 88 6/12 rounded to the nearest whole number
Answers
Answer: 88 1/2
Step-by-step explanation:
easy
Answer:
89
Step-by-step explanation:
How much change will I receive from $100 after spending $75.34 on paint?
Answers
Answer:
You will receive $24.66 in change.
Use sigma notation to represent the sum of the first seven terms of the following sequence: 4, 10, 16, …
Answers
Answer: 154
Step-by-step explanation:
\(a_1=4,\ d=6\quad \rightarrow \quad a_n=4+6(n-1)\quad \rightarrow \quad a_n=6n-2\\\\\\\sum^7_{n=1}6n-2\\\\\\a_1=4\\a_7=40\\\\\\S_n=\dfrac{a_1+a_7}{2}\cdot n\qquad =\dfrac{4+40}{2}\cdot 7\qquad =22\cdot 7\qquad =\large\boxed{154}\)
Answer:
154 I think
Step-by-step explanation:
Represent each of the following sequences as functions. In each case, state a domain, codomain, and rule for determining the outputs of the function. Also, determine if any of the sequences are equal.
(a) 1,14,19,116,…
(b) 13,19,127,181,…
(c) 1,−1,1,−1,1,−1,…
(d)cos(0),cos(π),cos(2π),cos(3π),cos(4π),…
Answers
The sequence cos(0),cos(π),cos(2π),cos(3π),cos(4π),… can be represented as a function k: N -> R, where N is the set of natural numbers and R is the set of real numbers. The domain of the function is the set of natural numbers, and the codomain is the set of real numbers. The function l: N -> {-1,1}, where l(n) = (-1)^(n).
The sequence 1,14,19,116,… can be represented as a function f: N -> N, where N is the set of natural numbers. The rule for determining the outputs of the function is as follows: f(1) = 1, f(2) = 14, f(3) = 19, f(4) = 116, and so on.
The sequence 13,19,127,181,… can be represented as a function g: N -> N, where N is the set of natural numbers. The rule for determining the outputs of the function is as follows: g(1) = 13, g(2) = 19, g(3) = 127, g(4) = 181, and so on. The domain of the function is the set of natural numbers, and the codomain is also the set of natural numbers. We can see that this sequence is not equal to any of the other sequences given.
The sequence 1,−1,1,−1,1,−1,… can be represented as a function h: N -> {-1,1}, where N is the set of natural numbers. The rule for determining the outputs of the function is as follows: h(1) = 1, h(2) = -1, h(3) = 1, h(4) = -1, and so on. The domain of the function is the set of natural numbers, and the codomain is the set {-1,1}. We can see that this sequence is equal to the function f: N -> {-1,1}, where f(n) = (-1)^(n+1).
To know more about function visit:-
https://brainly.com/question/30721594
#SPJ11
1000m divide by 100n written in form of 10z
Answers
The expression 1000m ÷ 100n in the form of 10z is 10m/10n, which simplifies to m/10n.
What is an expression?
In mathematics, an expression is a combination of one or more numbers, variables, and operations such as addition, subtraction, multiplication, division, exponentiation, and so on.
We can simplify the expression 1000m ÷ 100n as follows:
1000m ÷ 100n = (1000 ÷ 100) × (m ÷ n)
= 10 × (m ÷ n)
= 10m/n
To write this in the form of 10z, we need to find a value of z that makes 10z equal to 10m/n. Since 10z is equal to 10 times z, we can set 10 times z equal to 10m/n and solve for z as follows:
10z = 10m/n
Dividing both sides by 10, we get:
z = m/10n
Therefore, the expression 1000m ÷ 100n in the form of 10z is 10m/10n, which simplifies to m/10n.
To learn more about the expression, visit:
https://brainly.com/question/723406
#SPJ1
(a) use the extended euclidean algorithm to find the greatest common divisor of the given numbers and express it as the following linear combination of the two numbers. 6,066s 2,286t, where s
Answers
the Greatest Common Divisor is 252 and it can be expressed as the linear combination -2 * 6,066 + 3 * 2,286.
What is GCD?The greatest common divisor (GCD) is the biggest positive integer that divides two or more integers without leaving a remainder. It's also referred to as the greatest common factor (GCF) or the highest common factor (HCF). The Euclidean procedure, which continually divides the greater of the two integers by the smaller until a remainder of zero is obtained, is one way to calculate the GCD. The GCD is a crucial idea in mathematics, notably in number theory, and it has several applications in other disciplines, such as computer science and encryption. Finding the greatest common divisor of the coefficients of a linear equation in two variables is another popular geometry task.
How to solve?
The Greatest Common Divisor of 6,066 and 2,286 can be expressed as 252 = 6,066 * (-2) + 2,286 * 3. So, the GCD is 252 and it can be expressed as the linear combination -2 * 6,066 + 3 * 2,286.
To learn more about GCD, visit:
https://brainly.com/question/27227228
#SPJ4
Use an indirect proof to prove SSS Inequality Theorem (Theorem 5.14 ).
Answers
To prove the SSS Inequality Theorem using an indirect proof, we need to assume the opposite of what we are trying to prove and show that it leads to a contradiction.
The SSS Inequality Theorem states that for any triangle, the sum of the lengths of any two sides must be greater than the length of the third side.
Assume that there exists a triangle ABC where the sum of the lengths of two sides is not greater than the length of the third side. Without loss of generality, let's assume that AB + BC ≤ AC.
Now, consider constructing a triangle ABC where AB + BC = AC. This would mean that the triangle is degenerate, where points A, B, and C are collinear.
In a degenerate triangle, the sum of the lengths of any two sides is equal to the length of the third side. However, this contradicts the definition of a triangle, which states that a triangle must have three non-collinear points.
Therefore, our assumption that AB + BC ≤ AC leads to a contradiction. Hence, the SSS Inequality Theorem holds true, and for any triangle, the sum of the lengths of any two sides is greater than the length of the third side.
Learn more about Inequality here
https://brainly.com/question/30238989
#SPJ11
Write a story problem for 1/2 divided by 5. (This is for my friend please hurry).
Answers
Answer:
How many 1/2 cup servings are in a container of cheese that contains 5
cups altogether?
Step-by-step explanation: