Given the function f(x) = −5x2 − x + 20, find f(3).a. −28b. −13c. 62d. 64
Answers
After solving the given function for x = 3, the resultant answer is (A) -28.
What are functions?The exact same number of elements from Y is assigned to each element of X via a mathematical function from a set X to a set Y.
The function's domain and codomain are respectively referred to as the sets X and Y as a whole.
A function is a relationship between a number of inputs and outputs.
Simply described, a function is an association between inputs in which each input is coupled to exactly one output.
So, we have the function:
(x) = −5x² − x + 20
Now, calculate to find the value when: x = 3
Given that, we must determine the value of the function at x = 3.
Set x = 3 in the provided function, f(x)
f(3) = −5(3)² − x + 20
f(x) = -45 - 3 + 20 = -28
Therefore, after solving the given function for x = 3, the resultant answer is (A) -28.
Know more about functions here:
https://brainly.com/question/17043948
#SPJ1
Related Questions
A car travels a distance of 1280 metres at an average speed of 64 kilometres per hour.
Ра:
Calculate the time it takes for the car travel this distance,
Give your answer in seconds
Answers
Answer:
The answer is 20 hours
Step-by-step explanation:
This is becuase 1280 divided by 64 equals 20. There are no unit coversions.
In time t = 0.02 hour the car travels a distance of 1280 meters with a speed of 64 kilometers per hour.
Given that,
A car travels a distance of 1280 meters at an average speed of 64 kilometers per hour.
Speed is defined as when an object is in motion, the distance covered by that object per unit of time is called speed.
Here,
Time = distance/speed
Time. t = 1.280 / 64
t = 0.02 hours
Thus, In time t = 0.02 hour the car travels a distance of 1280 meters with a speed of 64 kilometers per hour.
Learn more about speed here:
https://brainly.com/question/7359669
#SPJ2
If the perimeter of a rectangle is 24 feet and on eof the sides has a lenght of x feet then the area of the rectangle is
Answers
If the perimeter of a rectangle is 24 feet and one of the sides has a length of x feet, the area of the rectangle is A = x (12 - x).
Let's consider a rectangle with one side measuring x feet. The perimeter of a rectangle is given by the formula
P = 2(l + w), where P represents the perimeter, l represents the length, and w represents the width.
In this case, since one of the sides has a length of x, we can substitute the values in the formula as follows:
24 = 2(x + w)
Simplifying the equation, we have
12 = x + w
To find the area of the rectangle, we use the formula A = lw, where A represents the area, l represents the length, and w represents the width. Since we know that one of the sides has a length of x, we can substitute x for the length, resulting in
A = xw
To determine the value of the width, we can rearrange the equation
12 = x + w to express w in terms of x, which gives w = 12 - x.
Substituting this value into the area formula, we have
A = x(12 - x)
This expression represents the area of the rectangle in terms of x.
Learn more about perimeter here:
https://brainly.com/question/68308
#SPJ11
a rectangular prism has a base with edge length 40 units, edge width 3 units, and height of 30 units. A triangular prism has a right triangular base with legs that are 60 units long and a height of 30 units
Answers
The ratio of the volume of the rectangular prism to the volume of the triangular prism is \(\frac{1}{15}\).
How to calculate the ratio between the volume of two prismsThe volume of two right prisms (\(V\)), cubic units, equals the product of the base area and its height, both in units. Thus, the ratio of both volumes is now calculated:
\(r = \frac{(40)\cdot (3)\cdot (30)}{\frac{1}{2}\cdot (60)^{2}\cdot (30) }\)
\(r = \frac{1}{15}\)
The ratio of the volume of the rectangular prism to the volume of the triangular prism is \(\frac{1}{15}\). \(\blacksquare\)
Remark
Statement is incomplete and poorly formatted. Correct and complete form is shown below:
A rectangular prism has a base with edge length 40 units, edge width 3 units, and a height of 30 units. A triangular prism has a right triangular base with legs that are 60 units long and a height of 30 units. Determine the ratio of the volume of the rectangular prism to the volume of the triangular prism.
To learn more on prisms, we kindly invite to check this verified question: https://brainly.com/question/318504
A grain silo is shaped like a cylinder. The diameter is 10 yards and the height is 25 yards. If the silo is 60% filled, what is the volume of grain in the silo? Round to the nearest tenth.
Answers
The volume of grain in the silo when it is 60% filled is approximately 1178.1 cubic yards.
What is Volume?A closed surface or object's volume is determined by its three dimensions and is represented mathematically.
The following formula determines a cylinder's volume:
V = πr²h
where r is the radius of the cylinder and h is the height.
The diameter of the silo is 10 yards, so the radius is 5 yards. The height of the silo is 25 yards.
To find the volume of the silo, we need to first calculate its total capacity, which is the volume of a completely filled cylinder:
V_total = πr²h
V_total = π(5²)(25)
V_total = 625π
To find the volume of grain in the silo when it is 60% filled, we need to find 60% of the total capacity:
V_grain = 0.6V_total
V_grain = 0.6(625π)
V_grain ≈ 1178.1 cubic yards (rounded to the nearest tenth)
Therefore, the volume of grain in the silo when it is 60% filled is approximately 1178.1 cubic yards.
Learn more about volume , visit :
brainly.com/question/1578538
#SPJ1
The first bookshelf in the science fiction section of a library can hold 2,226
books. The bookshelf has 7 shelves. Each shelf can hold the same number of
books. How many books can each shelf hold? Write an equation to help solve
this problem.
Let b = the number of books on a shelf. Then 7b = and b =
Answers
Answer: b= 318
Step-by-step explanation:
7b= 2226
b= 2226/7= 318
a phone signals from a transmitter that is 19km west and 36km south of it. what is the bearing from the phone to the transmitter give your answer to the nearest degree.
Answers
Answer:
152 .18 degrees
Step-by-step explanation:
See attached diagram
arctan (36/19) = 62.18 degrees
If North is zero....you will need to add 90 degrees= 152.18 degrees

answer pls!! A 12 inch vertical post casts a 24 inch shadow at the same time a nearby flower casts a 49 inch shadow.
How tall is the flower?
Answers
Which number is divisible by both three and nine?
Select the Hint button to view a hint.
A.21,369 B. 36,359 C. 48,618 D. 56,783
Answers
Answer:
answer is
A.21,369 or D. 56,783
Step-by-step explanation:
am not sure but am mostly sure it is D but i dont know i think is A to but am
99% is D
hope it helps
Answer:
Your answer is C 48,618
Step-by-step explanation:
if you add the sum up of all of the digits it is divisible by both three and nine.
can i plz get brainliest.
Given a and ß are the roots of the quadratic equation
-2x² - 5x + 6 = 0. Form the quadratic equation which has the roots 3x + ß and 3ß + a
Answers
The quadratic equation that has (3·x + β) ans (3·x + a) as the roots can be presented as follows;
9·x² - 7.5·x - 3 = 0
What is a quadratic equation?A quadratic equation is an equation that can be expressed in the form; y = a·x² + b·x + c, where, a ≠ 0, and a, b, and c are numbers.
The quadratic equation -2·x² - 5·x + 6 = 0, divided by a factor of -1 indicates that we get;
2·x² + 5·x - 6 = 0
The quadratic formula indicates that we get;
x = (-5 ± √(5² - 4 × 2 × (-6))/(2 × 2) = (-5 ± √(73))/4
Let a = (-5 + √(73))/4 and let β = (-5 - √(73))/4)
(3·x + ((-5 + √(73))/4)) × (3·x + (-5 - √(73))/4) = 9·x² + 3·x·(-5 - √(73))/4) + 3·x·(-5 + √(73))/4) + ((-5 + √(73))/4)) × (-5 - √(73))/4)
9·x² + 3·x·(-5 - √(73))/4) + 3·x·(-5 + √(73))/4) + ((-5 + √(73))/4)) × (-5 - √(73))/4) = 9·x² - 15·x/2 - 3 = 0
Therefore, the equation that has (3·x + β) ans (3·x + a) as roots is the equation
9·x² - 15·x/2 - 3 = 9·x² - 7.5·x - 3 = 0
Learn more on quadratic equations here; https://brainly.com/question/29179994
#SPJ1
find the number of primes less than 200 using the prin- ciple of inclusion–exclusion.
Answers
To find the prime number less than 200 using the principle of inclusion-exclusion, we first list all the primes less than 200, which are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, and 193.
Next, we use the principle of inclusion-exclusion to determine the prime numbers less than 200. The principle of inclusion-exclusion states that if we want to find the total number of elements in two or more sets, we must subtract the number of elements that are in the intersection of those sets.
In this case, we want to find the prime numbers less than 200, so we need to subtract the primes that are not less than 200. The only prime that is not less than 200 is 199, so we subtract it from the list of primes less than 200.
Using the principle of inclusion-exclusion, we get:
Total number of primes less than 200 = number of primes less than 200 - number of primes not less than 200
= 46 - 1
= 45
Therefore, there are 45 prime numbers less than 200 using the principle of inclusion-exclusion.
Visit here to learn more about prime numbers : https://brainly.com/question/30358834
#SPJ11
The box plot represents the number of tickets sold for a school dance.
A horizontal line labeled Number of Tickets sold that starts at 8, with tick marks every one unit up to 30. The graph is titled Tickets Sold for A Dance. The box extends from 17 to 21 on the number line. A line in the box is at 19. The lines outside the box end at 10 and 27.
Which of the following is the appropriate measure of variability for the data, and what is its value?
The IQR is the best measure of variability, and it equals 17.
The range is the best measure of variability, and it equals 4.
The IQR is the best measure of variability, and it equals 4.
The range is the best measure of variability, and it equals 17.
Answers
The IQR is the best measure of variability, and it equals 4.
Option C is the correct answer.
What is IQR?
The area between the middle quarters of the scores is known as the interquartile range (IQR). The Interquartile range is the appropriate measure of variability when a distribution is skewed and the median rather than the mean is utilized to demonstrate a central tendency. The middle half of your data set—the second and third quartiles—is represented by the interquartile range (IQR).
From the box plot, we can see that the box extends from 17 to 21 on the number line, with a line at 19 inside the box.
This means that Q1 is 17 and Q3 is 21.
The IQR is:
IQR = Q3 - Q1 = 21 - 17 = 4
Thus,
The IQR is the best measure of variability, and it equals 4.
Learn more about Interquartile range
brainly.com/question/29204101
#SPJ1
what's the answer for 1/2 of 3/5?
Answers
Answer:
3/10
Step-by-step explanation:
1
Use the properties of an Isosceles Triangle to solve for x and y.
AJKL is an isosceles triangle. Find the values of x and y

Answers
Answer:
x = 3y = 11Step-by-step explanation:
isosceles triangle
solve for x:
JK = KL
8x = 13x - 15
15 = 13x - 8x
15 = 5x
x = 3
solve for y:
180 = 76 + 2(5y - 3)
180 - 76 = 10y - 6
10y = 110
y = 11

In order to solve the equation 9x=−3(x+1/3y) for y , a student simplifies the equation as shown: Step 1: 9x=−3x+−3(1/3y) Step 2: 9x=−3x+−y Step 3: 9x−3x=−y Step 4: 6x=−y Step 5: y=−6x Which statement describes the error the student made in simplifying the equation?
Answers
The error the student made was not correctly distributing the -3 to the second term (1/3y) inside the parenthesis in Step 1. The student incorrectly wrote -3(1/3y) as -3y instead of -y.
By correctly distributing the -3, the proper simplification would lead to the final answer of y = -12x.
The error the student made in simplifying the equation occurred in Step 1.
To solve the equation 9x = -3(x + 1/3y) for y is as follows:
Step 1: Distribute the -3 to both terms inside the parenthesis:
9x = -3x - y
Step 2: Add 3x to both sides of the equation to isolate the term with y:
9x + 3x = -y
Step 3: Simplify the equation by combining like terms:
12x = -y
Step 4: To solve for y, multiply both sides of the equation by -1:
y = -12x.
For similar question on distributing.
https://brainly.com/question/29368683
#SPJ11
how many solution this equation have 3r-5=3r-5
Answers
Answer:
infinite solutions
Step-by-step explanation:
Hello!
Since 3r - 5 is on both sides of the equation we can put any number in for r and it would still be true so the answer is infinite solutions
The answer is infinite solutions
Hope this helps!
Assigned Media
Skill Builder
X 2.4.75
The telephone company offers two billing plans for local calls. Plan 1 charges $36 per month for unlimited calls and Plan 2 charges $17 per month plus $0.04 per call.
a. Use an inequality to find the number of monthly calls for which Plan 1 is more economical than Plan 2
b. Explain the meaning of the answer to part a.
Answers
Answer: a. 36-17 <0.04x ⇒ 475 < x
b. When the number of calls is higher than 475 , Plan 1 is more economical than Plan 2.
Step-by-step explanation:
Hi, to answer this question we have to write an inequality:
The cost of plan 1 (36) must be less (<) than the cost of plan 2 (fixed charge [17] plus the product of the charge per call [0.04] and the number of calls [x] )
a.36 < 17+ 0.04x
Solving for x
36-17 <0.04x
19 < 0.04x
19 /0.04 <x
475 < x
b. When the number of calls is higher than 475 , Plan 1 is more economical than Plan 2.
Four fifths of the 35 kittens finish their milk how many did not finish their milk
Explain it don’t give me just answer
Answers
Answer:
7 kittens didn't finish their milk
Step-by-step explanation:
4/5 of 35 = 28
35-28=7
can i have brainlist pls
Answer:
7 kittens
Step-by-step explanation:
\(\frac{4}{5}=\frac{y}{35}\)
5 · y = 4 · 35
5y = 140
5y ÷ 5 = 140 ÷ 5
y = 28
35 - 28 = 7
Find ∂z/∂u and ∂z/∂v. The variables are restricted to domains on which the functions are defined.
z = (x + y)ey, x = u3 + v3, y = u3 − v3
∂z/∂u = ∂z/∂v =
Answers
The partial derivatives of z = (x + y)ey, with respect to u and v can be computed using the chain rule. We can first find the partial derivatives of z with respect to x and y and then use the chain rule to express the partial derivatives of x and y with respect to u and v. For z, the partial derivatives with respect to x and y are ey and (x + y)ey respectively. For x and y, the partial derivatives with respect to u and v are 3u2 and 3v2 respectively. Combining these, we get ∂z/∂u = 3u2ey(x + y)ey and ∂z/∂v = 3v2ey(x + y)ey.
Since the variables are restricted to domains on which the functions are defined, we can substitute the values of x and y in terms of u and v in the above partial derivatives to get the final expressions.
Know more about chain rule here
https://brainly.com/question/5543508#
#SPJ11
A rectangle’s perimeter and its area have the same numerical value. The length of the rectangle is 6. What is the width of the rectangle in units?.
Answers
Answer:
Step-by-step explanation:
Formula
P = 2*w + 2*L
Area = L*w
Givens
Area = P
L = 6
Create equation and Solve
LW = 2w + 2L
6w = 2w + 2*6
6w = 2w + 12 Subtract 2w from both sides
6w - 2w = 12 Combine
4w = 12 Divide by 4
4w/4 = 12/4
w = 3
Check
Area = 6*3 = 18
Perimeter = 2*3 + 2*6
Perimeter = 6 + 12 Combine
Perimeter = 18
It does check.
can you find the proportion pwease :)

Answers
Answer: 15/10
Step-by-step explanation:
Answer:
15 cookies and 10 brownies
Step-by-step explanation:
PLEASE HELP 25points!
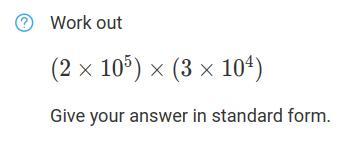
Answers
Answer:
2×10⁵ is the same as 200,000 and 3×10⁴ is the same as 30000 so this simply means you have to multiply the 2 figures and give the answer in standard form
200,000×30000
6000000000
which will be written as
6×10⁹
I hope this helps
I need answer to this problem soon

Answers
If two line segments are the same length, they are congruent.
What is congruency?We know two similar planer figures are congruent when we have sides or angles or both that are the same as the corresponding sides or angles or both.
If two line segments are the same length, they are congruent.
They do not have to be parallel, though. Any direction or angle on the plane is acceptable for them. There are two congruent line segments in the aforementioned figure. They are lying at various angles, as you can see. Any of the four endpoints can be moved around, and the length of the other segment will adjust to match the new one.
Congruent is equivalent to saying "equals" when referring to line segments. "The length of line LM equals the length of line NP," you could say. However, the right terminology for this in geometry is "line segments LM and NP are congruent" or "LM is congruent to NP".
learn more about line segments here :
https://brainly.com/question/25727583
#SPJ1
A right circular cylinder has a volume of 45pi. If the height of the cylinder is 5, what is the radius of the cylinder? Plz I need it Rn
Answers
Answer:
this is the answer I know.

Find the value of x :’)

Answers
Answer:
some of interior angles of hexagon = 720°
therefore,
720 = 121 + 96 + 101 + 162 + 90 + x
720 = 570 + x
729 - 570 = x
150 = x
please help!!
<RQT is a straight angle. What are m<RQS and m<TQS?

Answers
angle RQS = 101 degrees
angle TQS = 79 degrees
===================================================
Explanation:
A straight angle has a measure of 180 degrees. It's another way of saying "straight line".
The two angles shown add to 180.
We'll use this fact to solve for x.
(angleRQS) + (angleTQS) = angle RQT
(9x+2) + (7x+2) = 180
16x+4 = 180
16x = 180-4
16x = 176
x = 176/16
x = 11
Use this x value to determine the angles we're after.
angle RQS = 9x+2 = 9*11+2 = 99+2 = 101 degreesangle TQS = 7x+2 = 7*11+2 = 77+2 = 79 degreesCheck:
(angleRQS) + (angleTQS) = 101+79 = 180 which confirms the answer is correct.
A grinding process has an upper specification of 1.649 inches and a lower specification of 1.507 inches. A sample of parts had a mean of 1.57 inches with a standard deviaiton of 0.026 inches.
Round your answer to four decimal places.
What is the process capability index for this system?
Answers
Answer:
The process capability index for this system is 0.9103
Step-by-step explanation:
Upper specification = 1.649 inches
Lowe Specification = 1.507 inches
Mean = 1.57 inches
Standard Deviation = 0.026 inches
Process Capability Index = PCI
PCI = (Upper specification - lower specification)/6(standard deviation)
So, we get,
PCI = (1.649 - 1.507)/((6)(0.026))
PCI = 0.142/0.156
PCI = 0.9102564
To four decimal places, we get,
PCI = 0.9103
A rectangle has an area of 182 square feet and a base of 13 feet. What is the height?
Answers
Answer:
14 feet
Step-by-step explanation:
Area= base x height
Height=area/base
182/13=14
Rewrite, using the distributive
property.
16b-8b = ([?]-8)b = [?]b
![Rewrite, using the distributiveproperty.16b-8b = ([?]-8)b = [?]b](https://i5t5.c14.e2-1.dev/h-images-qa/contents/attachments/9Tmzv11947B9UtnbF6DBvWJp63YQcon7.png)
Answers
Answer:
8b
Step-by-step explanation:
You can factor the b-term out since b-term exists for all terms in the expression. By factoring out, you are basically dividing the factored term off and put it outside of the bracket, thus:
\(\displaystyle{16b-8b=\left(16-8\right)b}\)
Then evaluate and simplify:
\(\displaystyle{\left(16-8\right)b=8\cdot b}\\\\\displaystyle{=8b}\)
the volume of a sphere is increasing at a constant rate of 399 cubic centimeters per minute. at the instant when the volume of the sphere is 6161 cubic centimeters, what is the rate of change of the surface area of the sphere? the volume of a sphere can be found with the equation v
Answers
At the instant when the volume of the sphere is 6161 cm³, the rate of change of the surface area of the sphere is 68.5 cm² per minute.
The formula for the volume of the square is:
V = 4/3 πr³
Take the derivative with respect to t (time):
dV/dt = 4 πr² dr/dt
At an instant, the volume of the square is 6161 cm³
6161 = 4/3 πr³
r³ = (3/4) x 6161 / π = 1,470
r = 11.37 cm
dV/dt = 4 πr² dr/dt
399 = 4 π (11.37)² dr/dt
dr/dt = 0.24 cm/minute
The surface area of a sphere is:
A = 4 πr²
dA/dt = 8 πr dr/dt
= 8 π (11.37) (0.24) = 68.5
Hence, the rate of change of the surface area of the sphere is 68.5 cm² per minute.
Learn more about rate of change here:
https://brainly.com/question/22716418
#SPJ4
Please answer correctly !!!!!!!!!! Will
Mark brainliest !!!!!!!!!!!!

Answers
Answer:
Step-by-step explanation:
The discriminant is what's under the square root sign in the quadratic equation. The equation for the discriminant is \(b^{2}-4ac\), where b is the coefficient of x, a is the coefficient of \(x^{2}\), and c is the number with no variable attatched to it. If we plug in the numbers (\(17^{2} -4*4*3\)) it gives you 241, which is the discriminant. Since 241 is more than zero, it has 2 zeros. If the discriminant was 0, there'd be 1 zero, and less then zero there would be zero zeros.