Given the following data set, what is the shape of the data? 60, 68, 70, 72, 80, 84, 85, 90, 90, 92, 92, 94, 94, 94, 96, 96, 98, 100 Select one: O constant O skewed left O skewed right O symmetric
Answers
For a left skewed shape, the mean is typically less than the median. Also, the median is closer to the third quartile than to the first quartile
For a right skewed shape, the mean is typically greater than the median.
The first step is to determine the mean of the data set
Mean = (60 + 68 + 70 + 72 + 80 + 84 + 85 + 90 + 90 + 92 + 92 + 94 + 94 + 94 + 96 + 96 + 98 + 100)/18
Mean = 1463/18 = 81.3
Median = (90 + 92)/2 = 91
We can see that the mean is less than the median
We can go further by determining the first and third quartile
First quartile = 80
Third quartile = 94
The median is slightly closer to the third quartile than the first quartile.
Thus, the data set is left skewed
Answer:
the correct answer is The data is skewed right
Step-by-step explanation:
plato
Related Questions
-5X-3Y=-7 FIND 3 POINTS THAT SOLVE THE EQUATION
Answers
Answer:
(0, 7/3), (1, 2/3), (2, -1).
Step-by-step explanation:
Input 3 x coordinates into the equation and find the y. 0, 1, and 2 will do.
-5x - 3y = -7
Substitute variable.
-5(0) - 3y = -7
Remove the term multiplied by 0.
-3y = -7
Divide by -3.
y = -7/-3
-a/-b = a/b.
y = 7/3
This makes the coordinate (0, 7/3)
-5x - 3y = -7
Substitute variable.
-5(1) - 3y = -7
Multiply.
-5 - 3y = -7
Add 5 to both sides.
-3y = -2
Divide by -3.
y = -2/-3
-a/-b = a/b.
y = 2/3.
This makes the coordinate (1, 2/3)
-5x - 3y = -7
Substitute variable.
-5(2) - 3y = -7
Multiply.
-10 - 3y = -7
Add 10 to both sides.
-3y = 3
Divide by -3.
y = 3/-3
-a/a = -1.
y = -1.
This makes the coordinate (2, -1).
what is -7 + 3x = 8 - 2x
Answers
Answer: x = 3
Step-by-step explanation: -7 + 9 = 8 - 6
Write an equation of the line that
passes through the points (0,-5)
and (4,7).
Answers
Answer:
y = 3x - 5
Step-by-step explanation:
It passed through both points because of the y intercept and also the x intercept or contant matches up with the points
what does it mean to be a solution to an inequality
Answers
Answer:
Rule 1. Adding/subtracting the same number on both sides.
Example: The inequality x-2>5 has the same answer as the inequality x > 7.
Rule 2. Switching sides and changing the orientation of the inequality sign.
Example: The inequality 5-x> 4 has the same solutions as the inequality 4 < 5 - x.
Done ✔
Can someone help, I don't get the question

Answers
Step-by-step explanation:
f(n) = (-5). f(n-1) +15
f(1) = 3
for n = 2
f(2) = (-5).(3)+15 = -15+15 = 0
for n = 3
f(3) = (-5).0 +15 = 0+15 = 15
for n = 4
f(4) = (-5).(15) + 15 = -75 +15 = -60
so, the sequences are :
3, 0, 15, -60
\(\\ \sf\longmapsto f(n)=(-5)f(n-1)+15\)
Here
\(\\ \sf\longmapsto D_f=(0,\infty)\)
\(\\ \sf\longmapsto f(1)=3\)
\(\\ \sf\longmapsto f(2)=(-5)f(1)+15=(-5)(3)+15=-15+15=0\)
\(\\ \sf\longmapsto f(3)=(-5)(0)+15=0+15=15\)
\(\\ \sf\longmapsto f(4)=(-5)(15)+15=-75+15=-60\)
Write an equation for line L in mpoint-slope form and slope-intercept form.
L is perpendicular to y = 5x.

Answers
Answer:
X and A half marks Nathan and na ha na na he and na na he Meena new q me new me know if you
Step-by-step explanation:
erert4 Ka a manual Mrs Ann messed hall hall USS jam
What is the range of f(x) = |x| + 7?
−7 ≤ y < ∞
−∞ < y ≤ −7
0 ≤ y < ∞
7 ≤ y < ∞
Answers
When the domain is substituted, the Range of the function will be
7 ≤ y < ∞
How can we find Range ?The range of a function is the the spread of minimum value of the function to maximum value. We can find the range by substituting different domains into the function.
Given a function f(x) = |x| + 7
This |x| show that it is a modulus. That is, the domain will always be positive numerals.
The minimum domain = 0, so the minimum f(x) = 0 + 7 = 7
The maximum domain = ∞, so the maximum f(x) = ∞ + 7 = ∞
y = f(x)
Therefore, the range of of the function f(x) = |x| + 7 will be 7 ≤ y < ∞
Learn more about Range here: https://brainly.com/question/2264373
#SPJ1
Exponential Functions
HELP NEEDED! DUE TODAY

Answers
The function type is an exponential growth function
The function typeThe function y = 100(1.05)ˣ represents exponential growth, because the base (1.05) is greater than 1.
This means that as x (the number of years since the hotel opened) increases, the value of the function y (the cost per night at the hotel) increases exponentially.
The graph of the functionSee attachment
The key features of the graphFrom the attached graph, we have the key features of the graph of the function to be
The initial value is y = 100, which represents the cost per night when the hotel first opened.The growth factor is 1.05, which represents the 5% increase in cost per night every year since the hotel opened.As x increases, the value of y increases without bound,Read more about exponential functton at
https://brainly.com/question/11464095
#SPJ1

Lucas is planting grass on the shaded portions of the yard. What will be the total area covered by grass?
Answers
Complete Question:
Lucas is planting grass on the shaded portions of the yard. What will be the total area of covered by grass? Fill in the missing.
Part A= 12 x ? = ? ft²
Part B= 0.5 x ? x 9 = ?ft²
Part C= 0.5 x 7 x ? = ?ft²
Total Area= ?ft²
Answer:
\(A = 108ft^2\)
\(B = 27ft^2\)
\(C = 24.5ft^2\)
\(Area = 159.50ft^2\)
Step-by-step explanation:
Given
See attachment
From the attachment;
Part A is a rectangle with dimension 9ft by 12ft
So,
\(A = 12ft * 9ft\)
\(A = 108ft^2\)
Part B is a triangle with dimension: height = 6 and base = 9
The height is calculated as:
\(Height = 12ft - 6ft = 6ft\)
And the base is:
\(Base = 18ft - 9ft = 9ft\)
So, the area is:
\(B = 0.5 * 6ft * 9ft\)
\(B = 27ft^2\)
Part C is a triangle with dimension: height = 7 and base = 7
So, the area is:
\(C = 0.5 * 7 * 7ft^2\)
\(C = 24.5ft^2\)
Total Area is:
\(Area = A + B + C\)
\(Area = 108ft^2 + 27ft^2 + 24.5ft^2\)
\(Area = 159.50ft^2\)

I’m am so lost please help thank you all

Answers
Answer:
Step-by-step explanation:
148 people
Use this Ms. Yamagata is going to tile the floor of her rectangular bathroom that is 9 feet long and 7. feet wide. The cost per 6-inch tile is $0.50. The cost per 18-inch tile is $2.75. 4. If Ms. Yamagata uses 6-inch tiles, what are the least number of tiles that she needs to buy to cover the floor?
Answers
Answer:
252 6-inch tiles can cover the floor completely.
Step-by-step explanation:
For a rectangle of length L and width W, the area is:
A = L*W
In this case we know that the floor is 9ft long and 7 ft wide, then:
L = 9ft
W = 7ft
Because the tiles are in inches instead of ft, I will rewrite those measures on inches.
Here we need to use:
1ft = 12 in
Then:
L = 9ft = 9*( 12in) = 108 in
W = 7ft = 7ft*(12in) = 84 in
Then the area of the floor is:
A = 108in*84in = 9,072 in^2
In this case, Ms. Yamagata wants to only use 6-inch tiles to cover all the floor.
The area of a 6-inch tile is:
a = (6 in)*(6 in) = 36 in^2
The total number of 6-inch tiles that she needs to use, is the quotient between the area of the whole floor, and the area of one tile, this is:
N = A/a = (9,072 in^2)/(36 in^2) = 252
She needs to use exactly 252 tiles to cover the floor.
Which of the pp-values satisfy the following inequality?
5≥2p+1
Choose all answers that apply:
A: p=0
B: p=1
C: p=2
Answers
A: p=0
B: p=1
help pleaseeeeeeee guys :)?

Answers
Answer: plot one at -1 and the other at 5
Step-by-step explanation:
The Vertical intercept (0, 1/2)
suppose that prices of a gallon of milk at various stores in one town have a mean of $3.55 with a standard deviation of $0.14 . using chebyshev's theorem, what is the minimum percentage of stores that sell a gallon of milk for between $3.27 and $3.83 ? round your answer to one decimal place.
Answers
Therefore, the minimum percentage of stores that sell a gallon of milk for between $3.27 and $3.83 is 75%, rounded to one decimal place.
What is standard deviation?Standard deviation is a measure of the amount of variation or dispersion in a set of data values. It measures how spread out the data is from the mean or average value. A low standard deviation indicates that the data is closely clustered around the mean, while a high standard deviation indicates that the data is more spread out. It is calculated as the square root of the variance, which is the average of the squared differences from the mean.
Here,
Chebyshev's theorem states that for any dataset, regardless of its distribution, at least 1 - 1/k² of the data will fall within k standard deviations of the mean, where k is any positive number greater than 1. To find the minimum percentage of stores that sell a gallon of milk for between $3.27 and $3.83, we can first find how many standard deviations away from the mean these prices are:
$3.27 is (3.27 - 3.55)/0.14 = -2 standard deviations from the mean
$3.83 is (3.83 - 3.55)/0.14 = 2 standard deviations from the mean
Thus, the distance between $3.27 and $3.83 is 4 standard deviations (2 in each direction).
Using Chebyshev's theorem with k = 2 (since we want to know the minimum percentage within 2 standard deviations), we have:
=1 - 1/2²
= 1 - 1/4
= 0.75
This means that at least 75% of stores sell a gallon of milk for between $3.27 and $3.83.
To know more about standard deviation,
https://brainly.com/question/23907081
#SPJ1
2. ANSWER=
On one trip, the Skunk Train traveled at a constant speed of 20 mph.
Passengers enjoyed the scenery for the 2 hours they were riding the train.
How many miles was the trip?
A. 40 mi
B. 30 mi
C 20 mi
D
10 mi
Answers
Answer:
a yes udjwjwjwjwjwjwjwjwjw
yes men es chef
China and the United States are playing each other in the championship match of the 1999 Women's World Cup soccer tournament. Brandi Chastain of the U.S. team is about to take a penalty kick against the Chinese team's goalkeeper, Gao Hong. Chastain will kick the ball from 18 yards away from the goal at 120 miles per hour. How many seconds does the goalkeeper have to react, dive, and reach the ball before it crosses the goal line
Answers
Answer:
The goalkeeper has 0.306 seconds to react, dive, and reach the ball before it crosses the goal line.
Step-by-step explanation:
We use the following relation to solve this question:
\(v = \frac{d}{t}\)
In which v is the velocity, d is the distance, and t is the time.
Chastain will kick the ball from 18 yards away from the goal at 120 miles per hour.
Since the velocity is in miles per hour, the distance has to be in yards.
Each yard has 0.000568182 miles, so the ball will be kicked from 18*0.000568182 = 0.0102 miles.
This means that \(v = 120, d = 0.0102\)
How many seconds does the goalkeeper have to react, dive, and reach the ball before it crosses the goal line?
We have to find t, first in hours. So
\(v = \frac{d}{t}\)
\(120 = \frac{0.0102}{t}\)
\(120t = 0.0102\)
\(t = \frac{0.0102}{120}\)
\(t = 0.000085\)
An hour has 3600 seconds. So
3600*0.000085 = 0.306.
The goalkeeper has 0.306 seconds to react, dive, and reach the ball before it crosses the goal line.
let be a matrix, let and be vectors in , and let suppose and for some vectors and in . what fact allows you to conclude that the system is consistent? (note: and denote vectors, not scalar entries in vectors.)
Answers
The fact that and allows you to conclude that the system is consistent because if two vectors are equal, then their components must be equal.
Since and , we can set up the following linear system of equations:
Ax = b
where A is the matrix and x and b are the vectors. Since we know that and , then the system of equations is consistent. This is because if two vectors are equal, then their components must be equal. Therefore, if and , then
a1x1 + a2x2 = b1
a3x1 + a4x2 = b2
Since the two vectors are equal, then the components must be equal as well, so
a1x1 + a2x2 = a3x1 + a4x2
which can be rearranged to
(a1 - a3)x1 + (a2 - a4)x2 = b1 - b2
Since b1 - b2 is a constant, then the coefficient of x1 and x2 must both be 0, meaning that the system is consistent.
The fact that and allows you to conclude that the system is consistent because if two vectors are equal, then their components must be equal. This means that if and , then we can rearrange the system of equations to get (a1 - a3)x1 + (a2 - a4)x2 = b1 - b2, which implies that the coefficients of x1 and x2 must both be 0, meaning that the system is consistent.
Learn more about system is consistent here:
https://brainly.com/question/29095674
#SPJ4
Sombody hellllllllllllllp (90) points
Explanation and answer

Answers
Answer:
The value of z to balance the hanger is 2.75.Step-by-step explanation:
We know that:
11 = 4z (In balanced form)To balance the hanger, we must find the value of z such that if z is multiplied by 4, it will equal 11.
Work:
11 = 4z=> z = 11/4=> z = 2.75Hence, the value of z to balance the hanger is 2.75.
2x + 8
2 + 3
7x + 21
.
x +4
Answers
Answer:
\(60x + 86\)
Step-by-step explanation:
What part of an hour passes from 3:12 p.m. to 5:30 p.m.?
Answers
Answer:
2.3 hours
Step-by-step explanation:
From 3:12 pm to 4:12 pm, one hour passes.
From 4:12 pm to 5:12 pm, another hour passes.
From 5:12 pm to 5:30 pm, there are 18 minutes that pass.
Therefore, the total time elapsed is 2 hours and 18 minutes out of 60 minutes in an hour.
To convert this to a fraction, we can write:
2 hours + 18 minutes = 2 + 18/60 hours = 2.3 hours
So, 2.3/1 hour passes from 3:12 pm to 5:30 pm.
Convert 7% as a decimal
Answers
Answer:
0.07
Step-by-step explanation:
7/100
Answer:
it would be .07 i believe
Factor: 88a^2– 66b^2+ 11
Answers
Answer:
11a^2 - 6b^2+1
Step-by-step explanation:
Distribute
11(8a^2-6b^2+1
88a^2– 66b^2+ 11
Solution
88a^2– 66b^2+ 11
HOPE THIS HELPS!
Step 1: Equation at the end of step 1
((88 • (a2)) - (2•3•11b2)) + 11
Step 2: ((23•11a2) - (2•3•11b2)) + 11
Step 3/4: Pull out like terms/factors
88a2 - 66b2 + 11 = 11 • (8a2 - 6b2 + 1)
Answer: 11 • (8a2 - 6b2 + 1)

In studies examining the effect of humor on interpersonal attractions, McGee and Shevlin (2009) found that an individual’s sense of humor had a significant effect on how the individual was perceived by others. In one part of the study, female college students were given brief descriptions of a potential romantic partner. The fictitious male was described positively as being single and ambitious and having good job prospects. For one group of participants, the description also said that he had a great sense of humor. For another group, it said that he has no sense of humor. After reading the description, each participant was asked to rate the attractiveness of the man on a seven-point scale from 1 (very unattractive) to 7 (very attractive). A score of 4 indicates a neutral rating. The females who read the "great sense of humor" description gave the potential partner an average attractiveness score of M = 4.53 with a standard deviation of s = 1.04. If the sample consisted of n = 16 participants, is the average rating significantly higher than neutral (μ = 4)? Use a one-tailed test with α = .05
Answers
Answer:
The calculated value t = 2.038< 2.145 at 0.05 level of significance
Null hypothesis is accepted
There is the average rate is less than μ ≤ 4
Step-by-step explanation:
Step(i):-
The Population of the mean 'μ' =4
sample size 'n' = 16
sample mean 'x⁻' = 4.53
given sample standard deviation 's' = 1.04
level of significance α = 0.05
Step(ii):-
Null hypothesis:H₀ : There is no significance difference between two means
Alternative hypothesis : H₁: There is significance difference between two means
Test statistic
\(t = \frac{x^{-} - mean}{\frac{S}{\sqrt{n} } }\)
\(t = \frac{4.53-4}{\frac{1.04}{\sqrt{16} } }\)
t = 2.038
Degrees of freedom ν = n-1 = 16-1 =15
t₀.₀₂₅ = 2.145
Conclusion:-
The calculated value t = 2.038< 2.145 at 0.05 level of significance
Null hypothesis is accepted
There is the average rate is less than μ ≤ 4
Please help with this asap!! Would help a lot for me :)
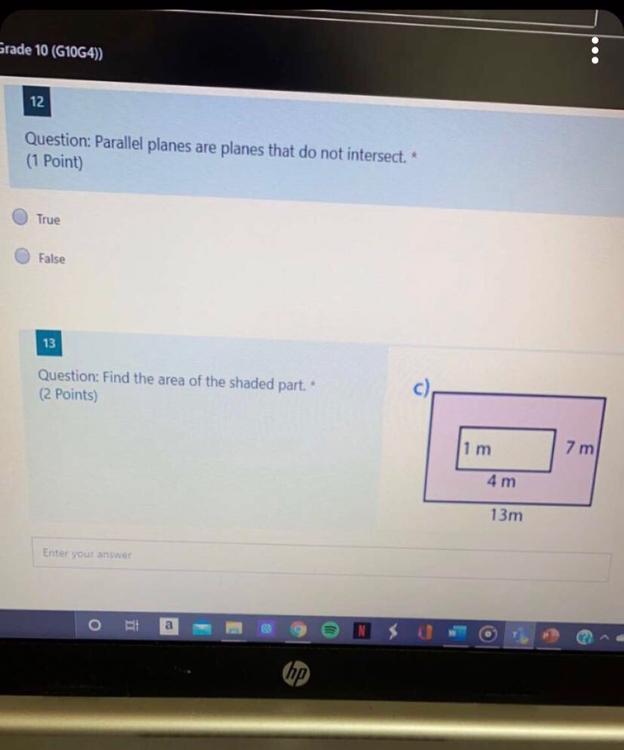
Answers
Answer:
answer 1 = true
answer 2 . Area of shaded part is 87m^2
explanation in the pic above

Answer:
Q1: True
Q2: 87 m squared
Step-by-step explanation:
Q1 is true because if two things are parallel may they be lines or planes, they can never intersect since the will always be parallel. As for Q2, you have to find the area of the smaller rectangle and the larger one. You then subtract the area of the smaller one from the larger one to find it's area. 4 times 1 is 4 so 4 is the smaller rectangles area. 7 times 13 is 91 so 91 is the larger rectangles area. 91 - 4 is 87. This means the area of the shaded part is 87 meters squared
Solve for x when -5x - 10=25
Answers
Answer: 3
Step-by-step explanation:
What values of x
and y
satisfy the system of equations {8x+9y=−36 x+7y=1}
Enter your answer as an ordered pair, like this: (42, 53)
If your answer includes one or more fractions, use the / symbol to separate numerators and denominators. For example, if your answer is (4253,6475),
enter it like this: (42/53, 64/75)
If there is no solution, enter "no"; if there are infinitely many solutions, enter "inf."
Answers
The solution to the system of equations is (x, y) = (-261/47, 44/47) as an ordered pair.
To solve the given system of equations:
Equation 1: 8x + 9y = -36
Equation 2: x + 7y = 1
We can use the method of substitution or elimination to find the values of x and y. Let's use the method of substitution:
From Equation 2, we can solve for x:
x = 1 - 7y
Substituting this value of x into Equation 1:
8(1 - 7y) + 9y = -36
8 - 56y + 9y = -36
-47y = -44
y = 44/47
Substituting the value of y back into Equation 2 to find x:
x + 7(44/47) = 1
x + 308/47 = 1
x = 1 - 308/47
x = (47 - 308)/47
x = -261/47
Therefore, as an ordered pair, the solution to the system of equations is (x, y) = (-261/47, 44/47).
Learn more about system of equation on:
https://brainly.com/question/12526075
A recent survey showed that exactly 38%
of people in a town buy the local
newspaper. There are 2450 people in the
town.
a) How many people in the town buy the
local newspaper?
b) How many people in the town do not
buy the local newspaper?
Answers
Answer:
a) .38 × 2,450 = 931 people buy the local newspaper.
b) 2,450 - 931 = 1,519 people do not buy the local newspaper.
Heights (cm) and weights (kg) are measured for 100 randomly selected adult males, and range from heights of 130 to 190 cm and weights of 40 to 150 kg. Let the predictor variable x be the first variable given. The 100 paired measurements yield x= 167.65 cm, y= 81.36 kg, r= 0.309, P-value= 0,002, and y= 106+1.15x. Find the best predicted value of y (weight) given an adult male who is 156 cm tall. Use a 0.10 significance level.
Answers
The best predicted weight of a person that is 156 cm is 285.4kg
We have the regression equation asy= 106+1.15
When the adult male is 156 cm tall the weight of this person would be calculated as:
y= 106+1.15*156
y = 106 + 179.4
y = 285.4
Hence we can arrive at the conclusion that the best predicted weight of a person that is 156 cm is 285.4kg
Read more on regression equation here:
https://brainly.com/question/26843436
#SPJ1
If a couple plans to have 9 children, what is the probability that there will be at least one boy? Assume boys and girls are equally likely. Is that probability high enough for the couple to be very confident that they will get at least one boy in 9 children?
Answers
Answer:
It is a 9/10 chance of having at least one boy. The probability is also high enough for the couple to be very confident in having at least one boy in 9 children.
Step-by-step explanation:
I listed all of the possible combinations below
GGGGGGGGG BGGGGGGGG
BBGGGGGGG BBBGGGGGG
BBBBGGGGG BBBBBGGGG
BBBBBBGGG BBBBBBBGG
BBBBBBBBG BBBBBBBBB
Total number of combinations with at least one boy is 9/10
This is a very high percentage, which means the couple is very likely to have at least one boy.
5. Judy isn't sure whether a credit card using the average daily balance method, a credit card using
the previous balance method, or a credit card using the adjusted balance method is right for her.
Regardless of the method used, Judy's APR will be 26%. Her last 30-day billing cycle was typical for
her, so she decided to calculate the amount of interest charged by each method to compare them.
The opening balance of her last 30-day billing cycle was $930, and it remained that amount for the
first 10 days of the billing cycle. She then made a purchase for $550, so her balance jumped to
$1480, and it remained that amount for the next 10 days. Judy then made a payment of $790, so her
balance for the last 10 days of the billing cycle was $690.
Help Judy decide which method is best for her based on her last 30-day billing cycle. (4 points: Part 1
- 1 point; Part II - 1 point; Part III - 1 point; Part IV-1 point)
Part I: What is Judy's average balance for her billing cycle?
Answers
Answer:1,203
Step-by-step explanation: