Given that segment KL is parallel to segment MN and that segment KN bisects segment ML, prove that segment KO is congruent to segment NO
Answers
If that segment KL is parallel to segment MN and that segment KN bisects segment ML, then segment KO is congruent to segment NO.
To prove that segment KO is congruent to segment NO, we need to show that triangle KNO is an isosceles triangle, with KO ≅ NO.
From the given information, we know that KL is parallel to MN, which means that angle KLN is congruent to angle MNL (corresponding angles). Also, KN bisects segment ML, which means that angle KNO is congruent to angle NMO (angle bisector theorem).
Therefore, we have:
angle KNO = angle NMO
angle KLN = angle MNL
Adding these two equations gives us:
angle KNO + angle KLN = angle NMO + angle MNL
But angle KLN + angle NMO + angle MNL = 180 degrees (as they form a straight line). So we can substitute this into the equation:
angle KNO + 180 degrees = 180 degrees
Simplifying, we get:
angle KNO = 0 degrees
This means that KO and NO are on the same line, so they must be congruent. Therefore, we have proven that segment KO is congruent to segment NO.
To learn more about congruent triangle, click on below link:
brainly.com/question/15064982
#SPJ11
Related Questions
The dimensions for a rectangular prism are x + 3 for the length, x + 2 for the width, and x for the height. What is the volume of the prism? Enter your answer as a polynomial in standard form.
Answers
Answer:
the answer will be x^3 + 2x^2 + 9x
Step-by-step explanation:
as :
volume = l* w* h
= X * (X + 2) * (X + 3)
= X ^ 2 + 2 X (X + 3)
= x ^2 (X + 3) + 2x (X + 3)
= x^3 + 3x +2x ^2 + 6x
= x^3 + 2x^2 + 9x
How many square yards of carpet
are needed to cover the floor of
a room that is 18 feet long and
12 feet wide? (1 yd = 3 ft)
Answers
The area of the floor required to cover using carpet is equal to 24 square yards .
To calculate the area of the room in square yards,
convert the dimensions from feet to yards and then find the product of the length and width.
1 yard (yd) = 3 feet (ft)
Room length in yards
= 18 feet / 3 feet/yd
= 6 yards
Room width in yards
= 12 feet / 3 feet/yd
= 4 yards
Now, find the area of the room in square yards:
Area = Length × Width
Area = 6 yards × 4 yards = 24 square yards
Therefore, 24 square yards of carpet area required to cover the floor of the room.
learn more about area here
brainly.com/question/1631786
#SPJ2
WILL MARK BRAINLIEST PLEASE ANSWER QUICK: In the equation y = 2x + 3, the number in front of the x is the _______
Answers
Answer:
Slope
Step-by-step explanation:
Slope-Intercept Form: y = mx + b
m = slope
b = y-intercept
We are given y = 2x + 3:
We define our variables:
m = 2
b = 3
Therefore, our slope is 2 and our y-intercept is 3.
Answer:
Slope
Step-by-step explanation:
Which equations are equivalent?
1. 2(6x+15-5x)+4=40
2. 40=2(15-x)+4
3. 12x+30-10x+4+40
A- 1 & 2
B- 2 & 3
C- 1 & 3
D- None of the equations are equivalent
Answers
Answer:
B
Step-by-step explanation:
The midpoint of JK is M(-2, -2) . If J(4, 3) , find the coordinates of the other endpoint.
Answers
Answer:
(-6, -1)
Step-by-step explanation:
x = (Xa + Xb)/2
-2 = (4 + Xb)/2
-2 = 4 + Xb
Xb = -6
y = (Ya + Yb)/2
-2 = (3 + Yb)/2
Yb + 3 = -4
Yb = -1

Help me please ASAP!!

Answers
Answer:
90
Step-by-step explanation:
25 POINTS!! A sample of radium has a weight of 1. 5 mg and a half-life of approximately 6 years.
a. How much of the sample will remain after 6 years 3 fea
Szean sear?
ery
b. Find a function which models the amount of radjum f(t), in mg, remaining
after 1 years.
Answers
With a half-life of approximately 6 years, 0.75 mg of the sample will remain after 6 years. The function which models the amount of radium f(t), in mg, remaining after t years is f(t) = 1.5 * (1/2)^(t/6).
The half-life of a radioactive material is the time it takes for half of the original amount of the material to decay.
After 6 years (which is equal to a half-life for a sample of radium), you would be left with 1/2 of the original amount of radium. This means that you would have 1.5 mg * 1/2 = 0.75 mg of the sample remaining after 6 years.
To model the amount of radium remaining after t years, we can use the equation:
f(t) = 1.5 * (1/2)^(t/6)
This equation uses the half-life of the radium (6 years) to calculate the fraction of the original amount that remains after t years. The function f(t) will give you the weight of the radium sample in milligrams remaining after t years.
For example, if you want to know the amount of radium remaining after 1 year, you can plug in t = 1 into the equation:
f(1) = 1.5 * (1/2)^(1/6) = 1.5 * (1/2)^(0.1666...) = 1.36 mg
This means that after 1 year, you would have approximately 1.36 mg of radium remaining.
Learn more about half-life here: https://brainly.com/question/29601725
#SPJ4
Solve the system by any method.
(3x – 4y = -5
(5x + 8y = -1

Answers
Answer:
( x , y ) = ( -1,1/2)
Step-by-step explanation:
Solve the equation for X
\(\left \{ {{x=-5/3+4/3y} \atop {5x+8y=-1}} \right.\)
Substitute the given value of x into the equation 5x + 8y = -1
5(-5/3+4/3y)+8y=-1
Solve the equation for Y
y=-1/2
Substitute the given value of y into the equation x = -5 / 3 + 4 / 3y
x=-5/3+4/3×1/2
Solve the equation for X
x=-1
The system solution is the computer pair
(x,y)=(-1,1/2)
Check if the ordered pair given to the solution of the system of equations
\(\left \{ {{3*(-1)-4*1/2=-5} \atop {5*(-1)+8*1/2=-1}} \right.\)
Simplify the equations
\(\left \{ {{-5=-5} \atop {-1=-1}} \right.\)
The ordered pair is the solution of the system of equations, since both equations are true
(x,y)=(-1,1/2)
the distribution of the heights of five-year-old children has a mean of 42.5 inches. a pediatrician believes the five-year-old children in a city are different. the pediatrician selects a random sample of 40 five-year-old children and measures their heights. the mean height of the sample is 41.7 inches with a standard deviation of 3.3 inches. a significance test at an alpha level of produces a p-value of 0.133. what is the correct interpretation of the p-value? there is a 13.3% chance that a sample mean at least as extreme as 41.7 inches will occur by chance if the true mean height of five-year-old children is 42.5 inches. assuming the true mean height of five-year-old children is 42.5 inches, there is a 13.3% probability that the null hypothesis is true by chance alone. there is a 13.3% probability that a sample mean of 41.7 inches will occur by chance alone if the true mean height of five-year-old children is 42.5 inches. assuming the true mean height of five-year-old children is 42.5 inches, there is an 86.7% probability that a sample mean height of 42.5 inches will occur by chance alone.
Answers
In this situation, the p-value should be interpreted as follows: "There is a 13.3% probability that a sample mean of 41.7 inches will occur by chance alone if the true mean height of five-year-old children is 42.5 inches."
The amount of evidence contradicting the null hypothesis is indicated by the p-value.
The null hypothesis in this scenario is that children aged five actually have a mean height of 42.5 inches.
If the null hypothesis is correct, the p-value represents the likelihood of finding a sample mean as extreme as 41.7 inches or more extreme.
We cannot rule out the null hypothesis because the p-value is higher than the usual significance level of 0.05, being 0.133.
This indicates that there is insufficient data to draw the conclusion that the city's mean five-year-old kid height differs considerably from 42.5 inches.
The right conclusion is that, if the true mean height of five-year-old children is 42.5 inches, there is a 13.3% likelihood that a sample mean of 41.7 inches will occur by chance alone.
This shows that, rather than reflecting a genuine difference in the population mean, the observed difference in the sample mean height may possibly be attributable to random variation.
For similar question on probability.
https://brainly.com/question/28185528
#SPJ8
Find the dimensions of a rectangle with perimeter 76 m whose area is as large as possible. (If both values are the same number, enter it into both blanks.)
I need to find the meters of the smaller and larger value.
Answers
To find the dimensions of a rectangle with a perimeter of 76 m that maximizes its area, we can use the concept of optimization.
By using the formulas for the perimeter and area of a rectangle, we can set up an equation and solve for the dimensions that yield the maximum area.
Let's assume the length of the rectangle is L and the width is W. The perimeter of a rectangle is given by the formula P = 2L + 2W, and the area is given by A = LW.
Given that the perimeter is 76 m, we have 2L + 2W = 76. Rearranging this equation, we can express W in terms of L as W = (76 - 2L) / 2.
Substituting this expression for W into the area formula, we have A = L * [(76 - 2L) / 2].
To find the dimensions that maximize the area, we can take the derivative of the area function with respect to L, set it equal to zero, and solve for L. By finding the critical point and checking the endpoints, we can determine the values of L and W that yield the maximum area.
After obtaining the values of L and W, we can calculate their respective measurements in meters, which will give us the dimensions of the rectangle with the largest possible area.
To learn more about perimeter click here:
brainly.com/question/7486523
#SPJ11
Please Hurry this is really important thank you

Answers
Answer:
68°
Step-by-step explanation:
a triangle hold 180° so 180-43=137 and G and H are almost the same value where G is 69° and H is 68°
Step-by-step explanation:
x°+43°+(x-1)°=180°(sum of all the interior angle of triangle is 180°
2x°+42°=180°
2x°=180°-42°
2x°=138°
x=138°/2°
:. x=69°
Now,
angle H= (x-1)°=69°-1°=68°
:. angle H= 68°
In square $ABCD$ with sides of length 4 cm, $N$ is the midpoint of side $BC$ and $M$ is the midpoint of side $CD$. What is the area of triangle $AMN$,
Answers
Consequently, the area of triangle $AMN$ is equal to $A = \frac{1}{2}bh = \frac{1}{2}(4)(2) = 4$ cm2.
The area of triangle $AMN$ in square $ABCD$ can be calculated using the formula for area of a triangle, $A = \frac{1}{2}bh$, where $b$ is the length of the base and $h$ is the height of the triangle.
Since side $BC$ has a length of 4 cm, we can determine that $N$ is located 2 cm away from point $B$ and 2 cm away from point $C$.
Similarly, we can conclude that $M$ is located 2 cm away from point $C$ and 2 cm away from point $D$.
Therefore, the base of triangle $AMN$ is equal to 4 cm, and the height of triangle $AMN$ is equal to 2 cm.
for such more questions on Consequently
https://brainly.com/question/26182883
#SPJ11
Commercials for chewing gum make claims about how long the flavor will last. In fact, some commercials claim that the flavor lasts too long, affecting sales and profit. Let’s put those claims to a test. Imagine a student decides to compare four different gums using five participants. Each randomly selected participant was asked to chew a different piece of gum each day for 4 days, such that at the end of the 4 days, each participant had chewed all 4 types of gum. The order of the gums was randomly determined for each participant. After 2 hours of chewing, participants recorded the intensity of flavor from 1 (not intense) to 9 (very intense). Here are some hypothetical data:
Answers
Analysing the data and evaluating the claims about the duration of flavor, we use analysis of variance (ANOVA) to compare the mean flavor intensities of the four gums.
Let's assume we have the following hypothetical data for the flavour intensity ratings:
Participant 1: Gum A: 7,Gum B: 6,Gum C: 8,Gum D: 7
Participant 2: Gum A: 6,Gum B: 5,Gum C: 7,Gum D: 6
Participant 3: Gum A: 8,Gum B: 7,Gum C: 9,Gum D: 8
Participant 4: Gum A: 7,Gum B: 6,Gum C: 8,Gum D: 7
Participant 5: Gum A: 6,Gum B: 5,Gum C: 7,Gum D: 6
We have 5 participants who each chewed 4 different types of gum (A, B, C, D) over 4 days. The flavor intensity ratings were recorded after 2 hours of chewing, ranging from 1 to 9.
To analyze the data and evaluate the claims about the duration of flavor, we can use analysis of variance (ANOVA) to compare the mean flavor intensities of the four gums. ANOVA helps determine if there is a statistically significant difference in the mean flavor intensities among the groups.
Here are the steps to conduct ANOVA:
Set up hypotheses:
Null hypothesis (H₀): The mean flavor intensities of the four gums are equal.
Alternative hypothesis (Hₐ): The mean flavor intensities of the four gums are not equal.
Calculate the sum of squares:
Calculate the total sum of squares (SST) by summing the squared differences between each observation and the overall mean.
Calculate the between-group sum of squares (SSB) by summing the squared differences between each group mean and the overall mean, weighted by the number of observations in each group.
Calculate the within-group sum of squares (SSW) by summing the squared differences between each observation and its respective group mean.
Calculate the degrees of freedom:
Degrees of freedom between groups (dfB) = Number of groups - 1
Degrees of freedom within groups (dfW) = Number of observations - Number of groups
Calculate the mean squares:
Mean square between groups (MSB) = SSB / dfB
Mean square within groups (MSW) = SSW / dfW
Calculate the F-statistic:
F-statistic = MSB / MSW
Determine the critical value or p-value:
Using the F-statistic and degrees of freedom, you can look up the critical value from an F-distribution table or use statistical software to calculate the p-value.
Compare the obtained F-value with the critical value or p-value:
If the obtained F-value is greater than the critical value (or if the p-value is less than the significance level, often 0.05), reject the null hypothesis and conclude that there is a significant difference in the mean flavor intensities among the gums.
If the obtained F-value is less than the critical value (or if the p-value is greater than the significance level), fail to reject the null hypothesis and conclude that there is not enough evidence to suggest a significant difference in the mean flavor intensities among the gums.
By following these steps, you can perform an ANOVA analysis to evaluate the claims about the duration of flavor and determine if there is a significant difference in the mean flavor intensities among the four different gums.
Learn more about ANOVA here:
https://brainly.com/question/30459773
#SPJ11
The vertices of a rectangle are at (−1, −5), (3, −5), (3, −7), and (−1, −7). What is the length of the shorter side of the rectangle? Enter your answer in the box
Answers
Answer:
4 units
Step-by-step explanation:
The length of the shorter side is equal to the difference in y-coordinates of two vertically opposite vertices. The y-coordinates of the vertices (-1, -5) and (3, -5) are both -5, so the vertical side between them is not the shorter side. The y-coordinates of the vertices (3, -7) and (-1, -7) are both -7, so the vertical side between them is the shorter side. The difference in the x-coordinates of these two vertices is 3 - (-1) = 4, so the length of the shorter side is 4 units.
Answer: Your answer is 2
Step-by-step explanation: I did the k12 quiz here's proof

PLEASE HELP ME I REALLY NEED IT

Answers
Divide 32,400 by twelve
32,400/12=2,700
2,700x4 equals the amount depreciated in 4 years which equals 10,800
Subtract 10,800 from the original value 32,400-10,800= 21,600
A is your answer
The radius of a circle is 17 m. Find its area in terms of pi.
Answers
Answer:
289m²
Step-by-step explanation:
Area of circle =πr²=π×17²=289m² when r=radius =17m
consider the sequence -5,1,7,13,19,25 write a recursive definition and a general formula for this sequence
Answers
Answer:
Formula: n+6
In mathematics, a recursive definition is used to define the elements in a set in terms of other elements in the set.
please answer
4. Suppose that for 3MA Forecast, my Mean Absolute Deviation (MAD) is \( 3.0 \) and my Average Error (AE) is \( -2.0 \). Does my forecast fail the bias test? a. Yes b. No
Answers
The answer is: a. Yes, the forecast fails the bias test.
To determine whether the forecast fails the bias test, we need to compare the Average Error (AE) with zero.
If the AE is significantly different from zero, it indicates the presence of bias in the forecast. If the AE is close to zero, it suggests that the forecast is unbiased.
In this case, the Average Error (AE) is -2.0, which means that, on average, the forecast is 2.0 units lower than the actual values. Since the AE is not zero, we can conclude that there is a bias in the forecast.
Therefore, the answer is:
a. Yes, the forecast fails the bias test.
Learn more about bias test from
https://brainly.com/question/32000527
#SPJ11
-2 ⅝ * (4 ⅓)=
plzz help
Answers
Answer:
Step-by-step explanation:
Change into improper fraction
\(-2\frac{5}{8}*4\frac{1}{3}=\frac{-21}{8}*\frac{13}{3}\\\\ = \frac{-7}{8}*\frac{13}{1}\\\\=\frac{-91}{8}\\\\=-11\frac{3}{8}\)
A grocery store sells three different quantities of sugar. A 1-pound bag costs $1.08, a 2-pound bag costs
$1.86, and a 3-pound bag costs $2.76. Enter the unit cost in price per pound for each. Complete the
description about how the unit cost changes as the quantity of sugar increases.
Answers
Answer:
for every pound is x + 10. x is originally 80
If a test of the model shows that it holds 8,000 ounces, will the bridge hold 1 ton? 8,000 ounces on the model is equal to _ ounces on the actual bridge. Convert ounces to pounds. The actual bridge can hold _ pounds. Therefore, the bridge will/will not hold 1 ton
Answers
The question is given as: If a test of the model shows that it holds 8,000 ounces, will the bridge hold 1 ton? 8,000 ounces on the model is equal to _ ounces on the actual bridge. Convert ounces to pounds. The actual bridge can hold _ pounds. Therefore, the bridge will/will not hold 1 ton.
In order to answer the question, let's first convert the 8,000 ounces to pounds as follows: 1 pound = 16 ounces. Therefore, 1 ounce = 1/16 pounds.
Now, 8,000 ounces = 8,000/16 = 500 pounds8,000 ounces on the model is equal to 500 pounds on the actual bridge.
Now, let's find out how many pounds one ton is: 1 ton = 2,000 pounds.
Therefore, the actual bridge can hold 2,000 pounds.
Thus, since 2,000 pounds is greater than 500 pounds, the bridge will hold 1 ton.
To know more about ton visit:
https://brainly.com/question/29851296
#SPJ11
use the difference of two squares to find the value of 612 - 392
Answers
Answer: 4 (153 - 98)
formula is a^2-b^2=(a+b)(a-b)
factor out the GCF:
4(153−98)
both terms are not perfect squares so
you cant factor it further.
what is 6 divided by 1/5
Answers
Answer:
30
Step-by-step explanation:
To do this, you can take your denominator (5) and multiply it by your whole number (6) to get 30. This is your new numerator (top number). Then you put the old numerator (1) at the bottom. This leaves you with 30 over 1 which is just 30.
Carpet sells for $4 per square foot and will cost you $616 to recarpet your rectangular room. if your room is 14 feet long, how many feet wide is it?
Answers
When carpet sells for $4 per square foot and will cost you $616 to carpet your rectangular room, if you room is 14 feet long then the width is 11 feet
Given,
The cost of Carpet per square foot = $4
Total cost of the carpet = $616
We know
Area of the rectangle = Length × Width
Length = 14 feet
Consider the width of the rectangular room as x
Then the area of the room = 14x
Total cost of carpet = Area of the rectangular room× Cost of carpet per foot
Substitute the values
14x×4=616
14x=154
x=11 feet
Hence, When carpet sells for $4 per square foot and will cost you $616 to carpet your rectangular room, if you room is 14 feet long then the width is 11 feet
Learn more about Area here
brainly.com/question/27683633
#SPJ4
A triangle has angle measures of 72∘ and 3∘. What is the measure of the third angle?
Answers
help me out i will give brainliest i’m in school help

Answers
Answer:
C: (4, -12)
Step-by-step explanation:
graph starts at 48 and keeps going down by 4 making the x intercept stop at 4. y intercept goes down by 4 but stops on the negative side of 12. so (4,-12)
A new neighborhood initially has 48 houses. The number of houses grows at a rate of 5% per month. Approximately how many houses will be in the neighborhood after 3 months?
Answers
Answer:
55.2
Step-by-step explanation: 5% of 48 is 2.4 and 2.4 x 3 = 7.2, 7.2 + 48 = 55.2
Foot Locker bought Nike's latest shoes for $140. It marked them up by 30%. what price did the foot locker sell Nike's latest shoes for?
Answers
Answer:
Sold for $182 Marked up $42
Step-by-step explanation:
just multiply 140 by 30% which is .3 as a decimal
when multiplied you get 42 so just add that to the original price and you get 182
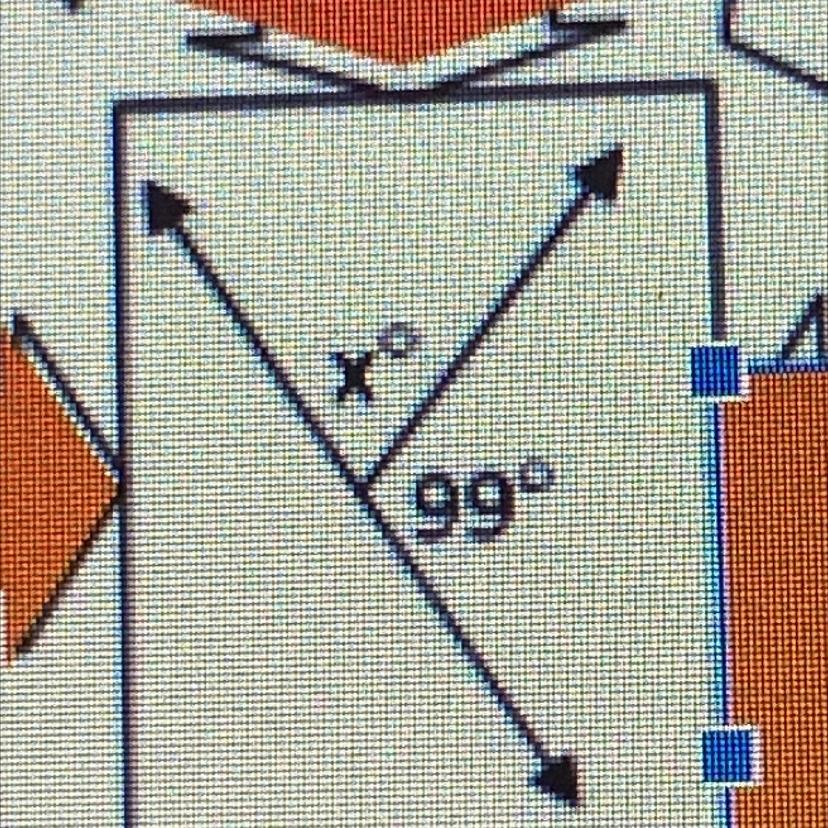
please help me find x.
Answers
Answer:
81°
Step-by-step explanation:
x + 99 = 180
x = 180 - 99
x = 81
Answer:
x = 81°
Step-by-step explanation:
The two angles shown add up to 180° because they are supplementary because they forma straight line. So, we can write an equation to model the situation:
x° + 99° = 180°
x = 81°
Please this one
Tickets cost $45 per person at the hockey arena. Beth is going to the game with her dad her sister and her friend they also charge a 6% sales tax her dad is buying the tickets for all of them how much money does he have to pay
Answers
$180 / 100 = $1.80 (1%)
X 106
= $190.80
Work: (4 people) x $45 (cost per ticket)= $180
$180 is the total cost before the sales tax, so to find the sales tax:
$180 x .06 ( percent in decimal form)= $10.80
Now we add the sales tax to the total cost for the 4 tickets:
$180+ $10.80= $190.80