Given box with
h= 2x-2 l = x + 5 w= 3x + 4 Write a polynomial that represents the volume of the box. Please use the palette below to enter your answer.
Answers
Here volume of the cuboid is 6x³ + 32x² + 2x - 40.
A cuboid's volume is calculated by summing its length, width, and height.
The number that is used to calculate how much room there is inside a cuboid is called its volume. A cuboid is a common three-dimensional form that surrounds us. Based on a form's parameters, such as its length, width, and height, the term "volume" is used to describe how much of that shape may be contained.
So Here,
height (h) = 2x - 2
Length (l) = 3x + 4
Breadth (b) = x + 5
Volume = l × b × h
= (3x + 4) × (x + 5) × (2x - 2)
= [(3x + 4)(x + 5)](2x - 2)
= (3x² + 13x + 20] (2x - 2)
Volume = 6x³ - 6x² + 38x² - 38x + 40x - 40
Volume (V) = 6x³ + 32x² + 2x - 40
To learn more about cuboid's volume
https://brainly.com/question/29424737
#SPJ4

Related Questions
Need help with this question

Answers
The properties of the linear equation are:
Slope: 3
y-intercept: y = 6
Equation: y = 3x + 6
How to write a Linear Equation in Slope Intercept Form?The formula for the equation of a Line in slope intercept form is expressed as:
y = mx + c
where:
m is slope
c is y-intercept
Now, the y-intercept is when x = 0 and as such in this case, it is:
c = 6
Slope between two coordinates is:
Slope = (y₂ - y₁)/(x₂ - x₁)
Slope = (6 - 3)/(0 - (-1))
Slope = 3
Thus, equation is:
y = 3x + 6
Read more about Slope Intercept Form at: https://brainly.com/question/1884491
#SPJ1
PLEASE HELP LOL
What is the missing perfect square?
25, 36, 49, _____, 81, 100
A)50
B)58
C)60
D) 64
Answers
Answer:
The answer is D. 64 because after 49 it is 64 (8*8=64 and 7*7=49)
Step-by-step explanation:
Answer:
64
Step-by-step explanation:
hurry please answer!!!

Answers
The gas used and miles are proportional for each scooter.
What is proportional relationship?Proportional relationships are relationships between two variables where their ratios are equivalent.
A proportional relationship is one in which two quantities vary directly with each other. We say the variable y varies directly as x if:
y = k x
for some constant k , called the constant of proportionality .
Therefore, let's check whether the scooter A and scooter B shows proportional relationships.
Hence,
For scooter A:
y = kx
where
x = miles coveredy = gas usedTherefore,
2 = 150 k
k = 2 /150
k = 1 / 75
Hence,
y = 1 / 75 x
From the table of scooter A, the ratio is constant, therefore, the relationships of gas used and distance covered is proportional for scooter A.
For the Scooter B the graph is also proportional because the ratios of the variables are constant.
learn more on proportional relationship here: https://brainly.com/question/12917806
#SPJ1
Which table represents a function?
A 2-column table with 4 rows. The first column is labeled x with entries negative 3, 0, negative 2, 8. The second column is labeled y with entries negative 1, 0, negative 1, 1.
A 2-column table with 4 rows. The first column is labeled x with entries negative 5, 0, negative 5, 6. The second column is labeled y with entries negative 5, 0, 5, negative 6.
A 2-column table with 4 rows. The first column is labeled x with entries negative 4, negative 2, negative 2, 0. The second column is labeled y with entries 8, 2, 4, 2.
A 2-column table with 4 rows. The first column is labeled x with entries negative 4, 3, 1, negative 4. The second column is labeled y with entries 2, 5, 3, 0.
Answers
A function must have one y-value for any given x-value.
Usually, if you see the same x-value in the x-column more than once, that's not going to be a function, because that usuall makes a single x-value pair with more than one y-value.
This would be NOT be a function, because x-value of 3 is paired with two different y-values.
x | y
3 7
4 8
3 9
6 7
Can you identify the function?
Parallel lines m and n are cut by a transversal t. Which two angles are corresponding angles? A. 1 and 5 B. 1 and 6 C. 1 and 2 D. 1 and 7

Answers
Answer:
1 and 5
Step-by-step explanation:
So basically corresponding angles are the angles which lie on the same line of the transversal
And also one of them will be an interior angle and the other a exterior angle
Answer:
D
Step-by-step explanation:
In ANOVA, which of the following is not affected by whether or not the population means are equal? between-samples estimate of o 2 within-samples estimate of o 2 None of these alternatives is correct.
Answers
In Analysis of variance, X (bar) is not affected by whether or not the population means are equal.
Analysis of variance is a statistical method for examining differences in means. It consists of a number of statistical models and the accompanying estimating techniques (such as the "variation" within and between groups). Ronald Fisher, a statistician, created Analysis of variance. The rule of total variance, on which the Analysis of variance is based, divides the observed variance in a given variable into components owing to various causes of variation.
ANOVA generalizes the t-test beyond two means by offering a statistical test to determine if two or more population means are equal. In other words, the Analysis of variance is employed to determine whether two or more means differ from one another.
To learn about Analysis of variance :
https://brainly.com/question/15084465
#SPJ4
DUE NOW PLEASE HELP!!!
Factor completely x2 − 10x + 25.
(x − 5)(x − 5)
(x + 5)(x + 5)
(x + 5)(x − 5)
(x − 25)(x − 1)
Answers
Answer:
(x - 5)(x - 5)
Step-by-step explanation:
\( {x}^{2} - 10x + 25 \: is \: the \: expansion \\ of \: {(x - 5)}^{2} \\ {(x - 5)}^{2} = (x - 5)(x - 5)\)
The complete factorization of the quadratic expression x² - 10x + 25 is (x - 5)(x - 5). Hence the first option is the right choice.
How to factor a quadratic expression?A quadratic expression of the form ax² + bx + c is factored by using the mid-term factorization method, which suggests that b should be broken in such two components that their product = ac. After this, we can factorize using the grouping method.
How to solve the given question?In the question, we are asked to factor the quadratic expression x² - 10x + 25 completely.
Comparing x² - 10x + 25 to ax² + bx + c, we get a = 1, b = -10, and c = 25.
To factor the expression we will use the mid-term factorization method, and try to break b in such two numbers whose product = ac.
Now, ac = 1 * 25 = 25. b = -10, which can be broken as -5, and -5.
Therefore, we can write the given expression as:
x² - 10x + 25
= x² - 5x - 5x + 25, mid-term factorization
= x(x - 5) -5(x - 5), grouping
= (x - 5)(x - 5), grouping.
Therefore, the complete factorization of the quadratic expression x² - 10x + 25 is (x - 5)(x - 5). Hence the first option is the right choice.
Learn more about mid-term factorization at
https://brainly.com/question/25829061
#SPJ2
based on the data you graphed, what type(s) of cancer appear to have a positive correlation with smoking rates?
Answers
The calculation for the correlation coefficient for the data graphed was 0.99 which is indicative of a strong positive correlation between smoking rates and lung cancer.
The data graphed showed a positive correlation between smoking rates and lung cancer. The correlation coefficient for the data was 0.99, which is very close to 1. This indicates a strong positive correlation between smoking rates and lung cancer. The formula for calculating the correlation coefficient is r = (NΣxy - (Σx)(Σy)) / √[(NΣx2 - (Σx)2)(NΣy2 - (Σy)2] where r is the correlation coefficient, N is the number of data points, Σx is the sum of all x-values, Σy is the sum of all y-values, Σxy is the sum of the products of the x and y values, and Σx2 and Σy2 are the sums of the squares of the x and y values respectively. The calculation for the correlation coefficient for the data graphed was 0.99 which is indicative of a strong positive correlation between smoking rates and lung cancer.
Learn more about correlation coefficient here:
https://brainly.com/question/27226153
#SPJ4
In one-way ANOVA, involving three groups, the alternative hypothesis would be considered correct if, in the population,a.all means were equalb.two means are equal but the third is differentc.all three means have different valuesd.either (b) or (c) above is true
Answers
There are at least two group means that are significantly different from one another, according to the alternative hypothesis (H a). The alternative hypothesis is adopted if the outcome is statistically significant.
What is anova test?You can use ANOVA to determine whether differences between data sets are statistically significant. It functions by examining the levels of variance present within each group using samples drawn from each.
The likelihood that the mean of a sample taken from the data will be different owing to chance increases if there is a lot of variance (spread of data away from the mean) among the data groups.
In addition to examining the variance within the data groups, ANOVA also considers sample size (the smaller the sample, the lower the likelihood that outliers will be randomly selected from it) and sample mean differences (the greater the difference between the sample means, the greater the likelihood that an outlier will be randomly selected from it).
hence, The alternative hypothesis is adopted if the outcome is statistically significant.
learn more about anova test click here:
https://brainly.com/question/25800044
#SPJ4
what is -3a + 2a - 7 + a, when a = ⅚
Answers
Answer: -7
Step-by-step explanation:
-3 (5/6) + 2 (5/6) - 7 + (5/6)
what is the distance from the point (12, 14, 1) to the y-z plane?
Answers
The problem involves finding the distance from a given point (12, 14, 1) to the y-z plane. The distance can be determined by finding the perpendicular distance from the point to the plane.
The equation of the y-z plane is x = 0, as it does not depend on the x-coordinate. We need to calculate the perpendicular distance between the point and the plane.
To find the distance from the point (12, 14, 1) to the y-z plane, we can use the formula for the distance between a point and a plane. The formula states that the distance d from a point (x₀, y₀, z₀) to a plane Ax + By + Cz + D = 0 is given by the formula:
d = |Ax₀ + By₀ + Cz₀ + D| / √(A² + B² + C²)
In this case, since the equation of the y-z plane is x = 0, the values of A, B, C, and D are 1, 0, 0, and 0 respectively. Substituting these values into the formula, we can calculate the distance from the point to the y-z plane.
To know more about distances click here: brainly.com/question/31713805
#SPJ11
PLEASE HELP A hot tub filled with 440 gallons of water is being
drained. After 1.5 hours, the amount of water had
decreased to 320 gallons.
The initial amount of water in the hot tub was
440 gallons, so (0, 440) is on the line.
After 1.5 hours, the amount of water had decreased
to 320 gallons, so (1.5, 320) is on the line.
Answers
Answer:
The slope of the line, m=-80 and
The equation of the line is, \(y=-80+440\)
Step-by-step explanation:
Given that initially the hot tub is filled with 440 gallons of water.
So, at time t=0, the amount of water = 440 gallons.
Further, after 1.5 hours, the amount of water had decreased to 320 gallons.
So, at time t=1.5 hours, the amount of water = 320 gallons.
The point (0,440) and (1.5, 320) are on the line.
So, the slope, m, of the line is
\(m=\frac{440-320}{0-1.5}=-\frac{120}{1.5}=-80\)
The equation of the line is
\(y-440=-80(x-0) \\\\\Rightarrow y-440=-80x \\\\\Rightarrow y=-80x+440\)
Hence, the slope of the line, m=-80 and the equation of the line is, \(y=-80+440\).
A)There are twice as many students in the math club as in the telescope club. Suppose there are $x$ students in the telescope club and $y$ students who are members of both clubs. Find an expression for the total number of students who are in the math club or the telescope club (or both). Give your answer in simplest form.
b)There are twice as many students in the math club as in the telescope club. Suppose there are students in the telescope club and students who are members of both clubs. Find an expression for the total number of students who are in the math club or the telescope club but not both. Give your answer in simplest form.
Answers
The number of students in the telescope club by $x$ and the number of students in the math club by $y$.
$y=2x$Now, suppose there are $z$ students who are members of both clubs. Then the total number of students who are in the math club or the telescope club (or both) is given by:$x + y - z$ Substituting $y=2x$ in the above expression, we get:$x + 2x - z=3x - z$ Hence, the expression for the total number of students who are in the math club or the telescope club (or both) is $3x - z$.b)The number of students who are in the math club but not in the telescope club is given by:$y-z$ And the number of students who are in the telescope club but not in the math club is given by:$x-z$ Adding these two expressions, we get the total number of students who are in the math club or the telescope club but not both:$ y-z+x-z $.
Learn more about students here:
https://brainly.com/question/25665799
#SPJ11
What is the solution to the equation 13(21−6x)=11−4(x+5) ? x=−8 x=−1 x=4 x=12
Answers
(-19, 55)
Summary: The solution to the system of equations y = -3x - 2 and 5x + 2y = 15 is (-19, 55).
Which are 15% off?
680 to 578
1120 to 896
340 to 289
250 to 212.50
Answers
680 to 578
340 to 289
250 to 212.50
Reasoning:
To find the percent of a number:
If the percentage is less than 100, we place a decimal point in front of the percent. Then, we multiply the percent by the whole.
For example, .15 x 680 = 102. Since 15% is less than 100, we place a decimal point in front of the 15. Then, we just multiplied it by the whole of 680.
We know that 102 = 15% of 680, so since that is the amount of money taken off the total, we subtract it: 680-102=578. Therefore, the new price is 578.
I did this for the rest of the questions, and there are 3 correct answers:
680 to 578
340 to 289
250 to 212.50
a and b are two statements such that "if a, then b " is a compound statement which will always be true unless a is true and b is false. what is that mean ?
Answers
"if a, then b" means that a is a sufficient condition for b, and that b is a necessary condition for a to be true. The statement is true unless a is true and b is false.
The statement "if a, then b" is known as a conditional statement, which is a type of logical statement that is often used in mathematics and other fields. In this case, the statement means that if statement a is true, then statement b must also be true. If a is false, then the truth value of b is not relevant, as the statement is considered true regardless.
The statement "if a, then b" is often written as "a → b" using logical symbols. The symbol "→" is read as "implies" or "if-then".
For example, consider the statements "If it is raining, then the ground is wet" (a → b). This statement is considered true unless it is raining and the ground is not wet, which is a contradiction. If it is not raining, the truth value of "the ground is wet" is not relevant to the truth of the conditional statement.
In summary, "if a, then b" means that a is a sufficient condition for b, and that b is a necessary condition for a to be true. The statement is true unless a is true and b is false.
To know more about Statements:
https://brainly.com/question/30244655
#SPJ11
the citizens of a city were asked to choose their favorite type of pet. the circle graph shows how the citizens answered. if 130,000 citizens answered the question, how many chose cat?
Answers
Based on the information provided, the circle graph represents the preferences of the citizens for their favorite type of pet. we can calculate the number of citizens who chose cats by multiplying the total number of citizens (130,000) by that percentage. If the graph shows that 40% of citizens chose cats, then the calculation would be 130,000 * 0.40 = 52,000 citizens who chose cats as their favorite pets.
According to the circle graph, we can see that the blue section represents the percentage of citizens who chose cats as their favorite type of pet. To find out the actual number of citizens who chose cats, we need to use the information that 130,000 citizens answered the question.
First, we need to determine what percentage of citizens chose cats. From the graph, it looks like the blue section represents about 35% of the total.
To calculate this percentage as a decimal, we divide 35 by 100:
35/100 = 0.35
Now we can use this decimal to find out how many citizens chose cats:
0.35 x 130,000 = 45,500
Therefore, approximately 45,500 citizens chose cats as their favorite type of pet.
Learn more about Percentage:
brainly.com/question/28269290
#SPJ11
I was wondering what\((3x + 5)\)multiplied by\((3x - 5)\)would be
Answers
Given the Multiplication:
\((3x+5)(3x-5)\)You need to remember the following formula that can be used to multiply binomials in that form:
\((a+b)(a-b)=a^2-b^2\)In this case:
\(\begin{gathered} a=3x \\ b=5 \end{gathered}\)Therefore, using the formula, you get:
\((3x+5)(3x-5)=(3x)^2-(5)^2=9x^2-25\)Hence, the answer is:
\(=9x^2-25\)Decide whether the triangles can be proven congruent by the given postulate or theorem. If not, state what information is needed. 11. AFLWAYLW by SAS
Answers
On this problem we have two triangles FLW and YLW. We know that the sides FL and LY are congruent and the side LW is shared between the two triangles. Therefore we know that two sides are congruent, we don't know however if the angles F and Y are congruents, there is no indication of that, so we can't prove that it is congruent, because we need to know if the angles are congruents.
-2 + x = -x + 2 what is x
Answers
Answer:
\(\large\boxed{\tt x=2}\)
Step-by-step explanation:
\(\textsf{We are asked to solve for the value of x.}\)
\(\textsf{We are given an equation where x is on both sides of the equation.}\)
\(\large\underline{\textsf{Solving;}}\)
\(\textsf{Begin solving by adding x to both sides of the equation to cancel out -x on the right}\)
\(\textsf{side of the equation. Afterwards, simplify the left side of the equation to evaluate}\)
\(\textsf{x.}\)
\(\large\underline{\textsf{Evaluating x;}}\)
\(\tt -2 + x= -x + 2\)
\(\textsf{Remove the -x on the right side by adding x to both sides of the equation.}\)
\(\tt -2 + x +\boxed{\tt x} = -x + \boxed{\tt x}+ 2\)
\(\tt -2 + 2x = 2\)
\(\textsf{Now, we should simplify the left side of the equation as there's only a whole number}\)
\(\textsf{on the right side of the equation.}\)
\(\textsf{Remove the -2 on the left side of the equation by adding 2 to both sides of the equation.}\)
\(\tt -2 + \boxed{\tt 2}+ 2x = 2 + \boxed{\tt 2}\)
\(\tt 2x = 4\)
\(\textsf{Lastly, divide both sides of the equation by 2 to find the value of x.}\)
\(\tt \frac{2x}{2} = \frac{4}{2}\)
\(\large\boxed{\tt x=2}\)
Answer:
\( \sf \: x = 2\)
Step-by-step explanation:
Now we have to,
→ Find the required value of x.
The equation is,
→ -2 + x = -x + 2
Then the value of x will be,
→ -2 + x = -x + 2
→ x + x = 2 + 2
→ 2x = 4
→ x = 4 ÷ 2
→ [ x = 2 ]
Hence, the value of x is 2.
Please someone help it confusing

Answers
1.false2.false3.true4.true5.true
Which system is represented in the graph? y > x2 + 4x – 5y > x + 5 y < x2 + 4x – 5y < x + 5 y ≥ x2 + 4x – 5y ≤ x + 5 y > x2 + 4x – 5y < x + 5

Answers
The given parabola has a vertex of (-2,-9), in vertex form the equation of the parabola is
\(\begin{gathered} y=(x-h)^2+k \\ \text{where} \\ (h,k)\text{ is the vertex} \\ \; \\ y=(x-h)^{2}+k \\ y=(x-(-2))^2+(-9) \\ y=(x+2)^2-9 \\ \text{Expand the binomial and simplify} \\ y=(x^2+4x+4)-9 \\ y=x^2+4x-5 \end{gathered}\)Since the shaded area of the parabola is in the top part, and uses a dashed line, the inequality therefore is
\(y>x^2+4x-5\)The linear inequality has a slope of 1, and a y-intercept of 5, which means that its linear equation is
\(y=x+5\)The same as the previous graph, since it has a shaded region in the top part and uses the dashed line, the linear inequality is
\(y>x+5\)Therefore, the graph is represented by the system
\(\begin{cases}y>x^2+4x-5 \\ y>{x+5}\end{cases}\)factorise x squared - 6x
Answers
The quadratic expression can be factorized to:
x*(x - 6)
How to factorize the expression?Here we have the expression:
x^2 - 6x
To factorize this, first, we need to find the roots, which are the solutions of:
x^2 - 6x = 0
Notice that one of the solutions is trivial, and it is x = 0.
If now we assume that x ≠ 0 and divide both sides by x, we get:
x - 6 = 0
x = 6
That is the other solution.
Now, for a square polynomial with the roots a and b, the factorized form is:
(x - a)*(x - b)
In this case, the roots are 0 and 6, then:
x^2 - 6x = (x - 0)*(x - 6) = x*(x - 6)
Learn more about quadratic expressions:
https://brainly.com/question/1214333
#SPJ1
ucas writes a numerical expression that has a value of 37. Which of the following expressions did Lucas write?
a
2.5^2+19\times2.5-16.75
b
2.5+19\times2.5-16.75
c
2.5^2+19\times2.5+16.75
d
2.5\times19+2.5^3-16.75
Answers
Answer:
a) 2.5^2+19\times2.5-16.75
Step-by-step explanation:
(2.5)² +(19× 2.5) - 16.75
= 6.25 + 47.5 - 16.75 = 37
If SF = 5x + 2, SK = 27, and KF = 3x - 1,
find KF.
Answers
Answer:
KF = 35
Step-by-step explanation:
Since it's a line with K in the middle, we know that the distance SF is the same as SK + KF.
(Start at S, first go to K, then continue to F. You've traveled the same distance as from S to F.)
SF = SK + KF
Let's put in the values we got.
5x + 2 = 27 + (3x -1)
Opening the parenthesis.
5x + 2 = 27 + 3x - 1
5x + 2 = 26 + 3x
Now let's subtract 3x from both sides.
2x + 2 = 26
Now, subtract 2 from both sides.
2x = 24
If we divide by 2...
x = 12
We know that...
KF = 3x -1
Since x is 12, let's put that in.
KF = 3 * 12 - 1 = 36 - 1 = 35
Answer: KF is 35 !
If 7 pounds of candy cost $16.17. How much does 1 pound of candy cost?
Answers
Answer:
$2.31
Step-by-step explanation :
$16.17 divided by 7
About 7/10 of the surface of the earth is covered with water. Express this as an equivalent fraction with 100 as the denominator. Fraction with 100 as denominators are known as per cent 50/100 means 50 per cent. So what percentage of the earth's surface is covered with water? What percentage covered with land
Answers
Answer:
70/100
Step-by-step explanation:
Surface of the earth covered with water = 7/10
Equivalent fraction of 7/10 with 100 as the denominator = 70/100
This means 70% of the earth surface is covered with water
Percentage covered with land = Total percentage - percentage covered with water
= 100/100 - 70/100
= 100-70/100
= 30/100
Percentage covered with land = 30%
H=4(x+3y)+2 make x the subject
Answers
When the formula is changed to x, the equation is x = 1/4(H - 2) - 3y
How to change the subject of formula to x?From the question, the equation is given as
H=4(x+3y)+2
Subtract 2 from both sides of the equation
So, we have the following equation
H - 2 =4(x+3y)+2 -2
Evaluate
So, we have the following equation
H - 2 =4(x+3y)
Divide by 4
So, we have the following equation
1/4(H - 2) = x +3y
Subtract 3y from both sides
x = 1/4(H - 2) - 3y
Hence, the solution for x is x = 1/4(H - 2) - 3y
Read more about subject of formula at
https://brainly.com/question/10643782
#SPJ1
The simplified solution for the x is given as x = [H - 2]/4 - 3y.
As mentioned in the question, for an equation H=4(x+3y)+2, we have to transform the equation in the subject of x.
The operational processes in mathematics for the functions to make the function or expression.
Here,
Simplification of the given function in a manner to the transposition of the variables from left to right,
H=4(x+3y)+2
H - 2 = 4(x+3y)
{H - 2}/4 = (x + 3y)
x = [H - 2]/4 - 3y
Thus, the simplified solution for the x is given as x = [H - 2]/4 - 3y.
Learn more about the subject of the formula here:
https://brainly.com/question/19107883
#SPJ1
Which table represents a linear function?
୦
X
1
no
2
4
y
-2
-6
-2
-6
Answers
Because the graph always has a consistent slope of +2, the table x|y-2| 4|0| 6|2| is an illustration of a linear function table.
In order for a table to represent a linear function, there must be a constant rate of change (slope) between any two points on the graph. In other words, the relationship between the x-values and y-values should follow a consistent pattern.
The correct table that represents a linear function is: x|y-2| 4|0| 6|2|This is because there is a constant rate of change of +2 between any two points on the graph. For example, when x goes from 2 to 4, y increases from -2 to 0. When x goes from 4 to 6, y increases from 0 to 2.
This constant rate of change indicates that the relationship between x and y is linear.
In summary, a table represents a linear function when there is a constant rate of change between any two points on the graph. The table x|y-2| 4|0| 6|2| is an example of a linear function table because there is a consistent slope of +2 between any two points on the graph.
For more questions on graph
https://brainly.com/question/29538026
#SPJ8
Compare the properties of each exponential function over the interval(0,4)
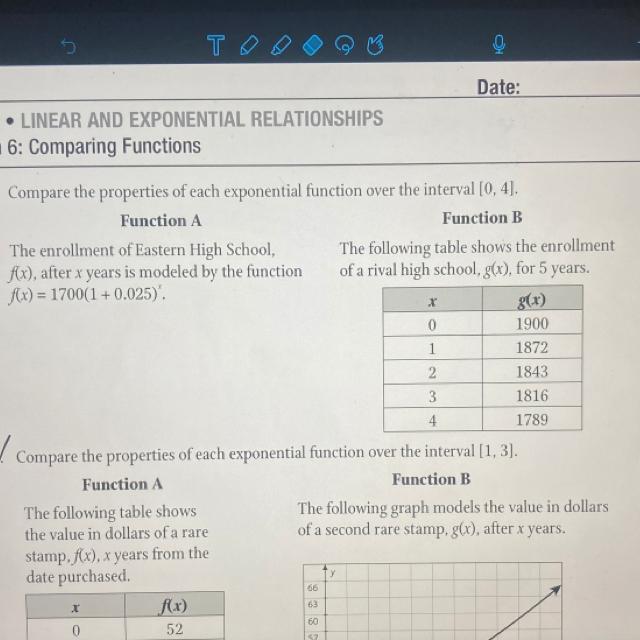
Answers
Answer:
sdgsehseh
Step-by-step explanation:
sehsdhsehsdhs